5-simplex - 5-simplex

5-simplex Hexateron (hix)
Rodzaj	jednolity 5-polytope
Symbol Schläfli	{3 ⁴ }
Diagram Coxetera
4 twarze	6	6 {3,3,3}
Komórki	15	15 {3,3}
Twarze	20	20 {3}
Krawędzie	15
Wierzchołki	6
Figura wierzchołka	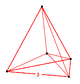5-komorowa
Grupa Coxetera	A ₅ , [3 ⁴ ], zamówienie 720
Podwójny	samo-dualne
Punkt bazowy	(0,0,0,0,0,1)
Circumradius	0.645497
Nieruchomości	wypukły , isogonal regularny , self-Dual

W geometrii pięciowymiarowej , 5- simplex to samouwielbienie regularne 5-polytope . Ma sześć wierzchołków , 15 krawędzi , 20 ścian trójkątnych , 15 czworościennych komórek i 6 ścianek po 5 komórek . Ma dwuścienny kąt cos ⁻¹ ( 1/5) lub około 78,46 °.

5-simplex to rozwiązanie problemu: utwórz 20 trójkątów równobocznych za pomocą 15 zapałek, gdzie każdy bok każdego trójkąta to dokładnie jedna zapałka.

Nazwy alternatywne

Może on być również nazywane hexateron lub heksa-5-Tope jako 6- szlifowanych Polytope w 5 wymiarach. Nazwa hexateron pochodzi z heksa- do zawierającą sześć aspekty i TERON (z ter- jest zniekształceniem tetra- ) do o aspekty czterech wymiarów.

Jonathan Bowers, heksateronowi nadano akronim hix .

Jako konfiguracja

Ta macierz konfiguracji reprezentuje 5-simplex. Wiersze i kolumny odpowiadają wierzchołkom, krawędziom, ścianom, komórkom i czterem ścianom. Liczby przekątne mówią, ile każdego elementu występuje w całym 5-simplex. Liczby niediagonalne mówią, ile elementów kolumny występuje w elemencie wiersza lub na nim. Macierz tej samouwielbienia simplex jest identyczna jak jej obrót o 180 stopni.

${\ Displaystyle {\ rozpocząć {bmatrix} {\ rozpocząć {matryca} 6 i 5 i 10 i 10 i 5 \\ 2 i 15 i 4 i 6 i 4 \\ 3 i 3 i 20 i 3 i 3 \\ 4 i 6 i 4 i 15 i 2 \\ 5 i 10 i 10 i 5 i 6 \ koniec {matryca}} \ koniec {bmatrix}}}$

Regularne współrzędne kartezjańskie heksateronu

Hexateron może być wykonana z 5 komórek przez dodanie 6. wierzchołka tak, że jest w równej odległości od każdego z pozostałych wierzchołków 5-komórce.

Te współrzędne kartezjańskie w wierzchołkach pochodzenie skoncentrowane regularnych hexateron o długości krawędzi 2 są:

{\ Displaystyle {\ rozpocząć {wyrównane} i \ lewo ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1 } {\ sqrt {6}}}, \ {\ tfrac {1} {\ sqrt {3}}}, \ \ pm 1 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1} {\ sqrt {6}}}, \ - {\ tfrac {2} {\ sqrt {3}}}, \ 0 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}} , \ - {\ tfrac {\ sqrt {3}} {\ sqrt {2}}}, \ 0, \ 0 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15 }}}, \ - {\ tfrac {2 {\ sqrt {2}}} {\ sqrt {5}}}, \ 0, \ 0, \ 0 \ right) \\ [5pt] & \ left (- { \ tfrac {\ sqrt {5}} {\ sqrt {3}}}, \ 0, \ 0, \ 0, \ 0 \ right) \ end {aligned}}}

Wierzchołki 5-simplex można prościej umieścić na hiperpłaszczyźnie w 6-przestrzeni jako permutacje (0,0,0,0,0,1) lub (0,1,1,1,1,1). Konstrukcja ta może być postrzegana jako fasety odpowiednio 6-ortopleksu lub rektyfikowanego 6-sześcianu .

Wyświetlane obrazy

rzuty ortograficzne
_K Coxeter samolot	A ₅	A ₄
Wykres
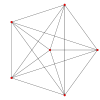
Symetria dwuścienna	[6]	[5]
_K Coxeter samolot	A ₃	A ₂
Wykres
Symetria dwuścienna	[4]	[3]

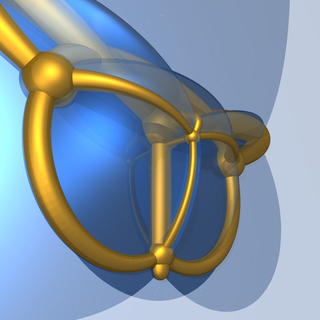Rzut stereograficzny 4D na 3D diagramu Schlegela 5D do 4D heksateronu.

Niższe formy symetrii

Niższa forma symetrii to piramida 5-komórkowa () v {3,3,3}, z [3,3,3] porządkiem symetrii 120, skonstruowana jako podstawa 5-komórkowa w hiperpłaszczyźnie 4-przestrzeni i wierzchołku punkt nad hiperpłaszczyzną. Pięć boków piramidy jest zbudowanych z 5-ogniwowych komórek. Są one postrzegane jako figury wierzchołkowe ściętych regularnych 6-polytopów , jak ścięty 6-sześcian .

Inną formą jest {} v {3,3}, z [2,3,3] porządkiem symetrii 48, połączeniem prostopadłego digonu i czworościanu, przesuniętego ortogonalnie, ze wszystkimi parami wierzchołków połączonymi pomiędzy. Inną formą jest {3} v {3}, z [3,2,3] porządkiem symetrii 36 i rozszerzoną symetrią [[3,2,3]], rząd 72. Reprezentuje połączenie 2 ortogonalnych trójkątów, ortogonalnie przesuniętych, ze wszystkimi parami wierzchołków połączonymi między.

Są one widoczne na figurach wierzchołków zwykłych 6- polytopów z bitruncated i tritruncated, takich jak bitruncated 6-cube i tritruncated 6-simplex . Etykiety krawędzi w tym miejscu reprezentują typy ścian wzdłuż tego kierunku, a zatem reprezentują różne długości krawędzi.

Figury wierzchołkowe dla obciętych 6-simplexów
() wer. {3,3,3}		{} wersja {3,3}		{3} wersja {3}

obcięty 6-simplex	obcięty sześcian	bitruncated 6-simplex	bitruncated 6-cube	tritruncated 6-simplex

Złożony

Związek dwóch 5-simplexów w podwójnych konfiguracjach można zobaczyć w tym rzucie płaszczyzny A6 Coxetera , z czerwonymi i niebieskimi 5-simplex wierzchołkami i krawędziami. Ten związek ma symetrię [[3,3,3,3]], rząd 1440. Przecięcie tych dwóch 5-simplexów jest jednorodnym dwukierunkowym 5-simplexem . = ∩ .

Powiązane jednolite 5-polytopy

Jest to pierwsza w serii wymiarowej jednolitych polytopów i plastrów miodu, wyrażona przez Coxetera jako seria 1 _3k . Zdegenerowany 4-wymiarowy przypadek istnieje jako 3-sferyczne płytki, czworościenny dwuościan .

1 _3k dane wymiarowe
Przestrzeń	Skończone				Euklidesa	Hiperboliczny
n	4	5	6	7	8	9
Grupa Coxetera	A ₃ A ₁	A ₅	D ₆	E ₇	${\ displaystyle {\ tilde {E}} _ {7}}$ = E ₇⁺	${\ displaystyle {\ bar {T}} _ {8}}$ = E ₇⁺⁺
Diagram Coxetera
Symetria	[3 ^−1,3,1 ]	[3 ^0,3,1 ]	[3 ^1,3,1 ]	[3 ^2,3,1 ]	[[3 ^3,3,1 ]]	[3 ^4,3,1 ]
Zamówienie	48	720	23,040	2,903,040	∞
Wykres					-	-
Nazwa	1 _{3, -1}	1 ₃₀	1 ₃₁	1 ₃₂	1 ₃₃	1 ₃₄

Jest to pierwsza w serii wymiarowej jednolitych polytopów i plastrów miodu, wyrażonych przez Coxetera jako seria 3 _k1 . Zdegenerowany 4-wymiarowy przypadek istnieje jako 3- kulowe płytki, czworościenny hoszoedr .

3 figury wymiarowe _k1
Przestrzeń	Skończone				Euklidesa	Hiperboliczny
n	4	5	6	7	8	9
Grupa Coxetera	A ₃ A ₁	A ₅	D ₆	E ₇	${\ displaystyle {\ tilde {E}} _ {7}}$ = E ₇⁺	${\ displaystyle {\ bar {T}} _ {8}}$ = E ₇⁺⁺
Diagram Coxetera
Symetria	[3 ^−1,3,1 ]	[3 ^0,3,1 ]	[[3 ^1,3,1 ]] = [4,3,3,3,3]	[3 ^2,3,1 ]	[3 ^3,3,1 ]	[3 ^4,3,1 ]
Zamówienie	48	720	46,080	2,903,040	∞
Wykres					-	-
Nazwa	3 _{1, -1}	3 ₁₀	3 ₁₁	3 ₂₁	3 ₃₁	3 ₄₁

Polytope 5-simplex, as 2 ₂₀ jest pierwszym w serii wymiarowej 2 _2k .

2 _2k figur o n wymiarach
Przestrzeń	Skończone			Euklidesa	Hiperboliczny
n	4	5	6	7	8
Grupa Coxetera	A ₂ A ₂	A ₅	E ₆	${\ displaystyle {\ tilde {E}} _ {6}}$ = E ₆⁺	E ₆⁺⁺
Diagram Coxetera
Wykres				∞	∞
Nazwa	2 _{2, -1}	2 ₂₀	2 ₂₁	2 ₂₂	2 ₂₃

Regularne 5-simplex jest jednym z 19 jednolitego polytera na podstawie [3,3,3,3] Grupa Coxetera , wszystkie przedstawione tu w ₅ Coxeter płaszczyzn prostopadłych występów . (Wierzchołki są kolorowane zgodnie z kolejnością zachodzenia na siebie projekcji, czerwony, pomarańczowy, żółty, zielony, cyjan, niebieski, fioletowy z coraz większą liczbą wierzchołków)

Uwagi

Bibliografia

Gosset, T. (1900). „O regularnych i semi-regularnych figurach w przestrzeni n wymiarów”. Posłaniec matematyki . Macmillan. pp. 43–.
Coxeter, HSM :
- - (1973). „Tabela I (iii): Regularne polytopes, trzy regularne polytopes w n-wymiarach (n≥5)”. Regular Polytopes (3rd ed.). Dover. pp. 296 . ISBN 0-486-61480-8.
- Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C .; Weiss, Asia Ivic, wyd. (1995). Kalejdoskopy: wybrane pisma HSM Coxeter . Wiley. ISBN 978-0-471-01003-6.
  - (Przekaz 22) - (1940). „Regularne i pół regularne Polytopes I” . Math. Zeit . 46 : 380–407. doi : 10.1007 / BF01181449 . S2CID 186237114 .
  - (Przekaz 23) - (1985). „Regularne i pół-regularne Polytopes II” . Math. Zeit . 188 (4): 559–591. doi : 10.1007 / BF01161657 . S2CID 120429557 .
  - (Przekaz 24) - (1988). „Regularne i Semi-Regular Polytopes III” . Math. Zeit . 200 : 3–45. doi : 10.1007 / BF01161745 . S2CID 186237142 .
Conway, John H .; Burgiel Heidi; Goodman-Strass, Chaim (2008). „26. Hemicubes: 1 _n1 ”. Symetrie rzeczy . p. 409. ISBN 978-1-56881-220-5.
Johnson, Norman (1991). „Uniform Polytopes” (Rękopis). Cite Journal wymaga |journal=( pomoc )
- Johnson, NW (1966). Teoria jednolitych polytopów i plastrów miodu (PhD). Uniwersytet w Toronto.

Linki zewnętrzne

Olshevsky, George. „Simplex” . Glosariusz hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
Polytopy o różnych wymiarach , Jonathan Bowers
Słowniczek wielowymiarowy

v t mi Zasadnicze wypukłe regularne i jednolite polytopy o wymiarach 2–10
Rodzina	A _n	B _n	I ₂ (p) / D _n	E ₆ / E ₇ / E ₈ / F ₄ / G ₂	H _n
Regularny wielokąt	Trójkąt	Plac	p-gon	Sześciokąt	Pięciokąt
Jednolity wielościan	Czworościan	Ośmiościan • Sześcian	Demicube		Dwunastościan • Icosahedron
Jednolity 4-polytope	5-komorowa	16-ogniwowy • Tesseract	Demitesseract	24 ogniwa	120 ogniw • 600 ogniw
Jednolity 5-polytope	5-simplex	5-ortoplex • 5-kostka	5-demicube
Jednolity 6-polytope	6-simplex	6-ortoplex • 6-cube	6-demicube	1 ₂₂ • 2 ₂₁
Jednolity 7-polytope	7-simplex	7-ortoplex • 7-kostka	7-demicube	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Jednolity 8-polytope	8-simplex	8-ortoplex • 8-kostka	8-demicube	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Jednolity 9-polytope	9-simplex	9-ortoplex • 9-kostka	9-demicube
Jednolity 10-polytope	10-simplex	10-ortoplex • 10-kostka	10-demicube
Jednolity n - polytope	n - simplex	n - ortopleks • n - sześcian	n - demicube	1 _k2 • 2 _k1 • k ₂₁	n - pięciokątny polytope
Tematy: Rodziny polytopów • Regularne polytopy • Lista regularnych polytopów i związków

Polytopes A5
t ₀	t ₁	t ₂	t _0,1	t _0,2	t _1,2	t _0,3
t _1,3	t _0,4	t _0,1,2	t _0,1,3	t _0,2,3	t _1,2,3	t _0,1,4
t _0,2,4	t _0,1,2,3	t _0,1,2,4	t _0,1,3,4	t 0, _{1, 2, 3, 4}

Languages

In other projects