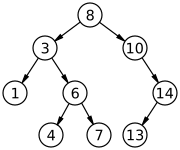
Drzewo wyszukiwania binarnego - Binary search tree

Drzewo wyszukiwania binarnego
Drzewo wyszukiwania binarnego
Rodzaj	drzewo
Wynaleziony	1960
Wynalezione przez	PF Windley, AD Booth , AJT Colin i TN Hibbard
Złożoność czasowa w notacji dużego O
Algorytm
Algorytm
Przestrzeń
Szukaj
Wstawić
Kasować

Drzewo wyszukiwania binarnego o rozmiarze 9 i głębokości 3, z 8 u podstawy. Liście nie są rysowane.

W informatyce , o drzewo binarne wyszukiwania ( BST ), zwany również zamówił lub sortowane drzewo binarne , jest zakorzenione binarne drzewo struktury danych , którego wewnętrzne węzły każdego sklepu kluczowym większe niż wszystkie klucze w lewym poddrzewie węzła i mniej niż w jego prawe poddrzewo. Drzewo binarne to rodzaj struktury danych do przechowywania danych, takich jak liczby, w zorganizowany sposób. Drzewa wyszukiwania binarnego umożliwiają wyszukiwanie binarne w celu szybkiego wyszukiwania, dodawania i usuwania elementów danych i mogą być używane do implementacji zestawów dynamicznych i tabel wyszukiwania . Kolejność węzłów w środkach BST że każdego porównania przeskakuje o połowę pozostałego drzewa, więc cała wyszukiwanie zajmuje czas proporcjonalny do tej binarnej logarytmu liczby przedmiotów przechowywanych w drzewie. Jest to znacznie lepsze niż liniowy czas potrzebny do znalezienia elementów według klucza w (nieposortowanej) tablicy, ale wolniejsze niż odpowiednie operacje na tablicach mieszających . Zbadano kilka wariantów binarnego drzewa poszukiwań.

Definicja

Drzewo wyszukiwania binarnego to zakorzenione drzewo binarne , którego węzły wewnętrzne przechowują klucz (i opcjonalnie skojarzoną wartość), a każde z nich ma dwa wyróżniające się drzewa podrzędne, zwykle oznaczane jako left i right . Drzewo dodatkowo spełnia właściwość wyszukiwania binarnego : klucz w każdym węźle jest większy lub równy dowolnemu kluczowi przechowywanemu w lewym poddrzewie i mniejszy lub równy dowolnemu kluczowi przechowywanemu w prawym poddrzewie. Liście (końcowe węzły) drzewa nie zawierają klucza i nie mają struktury, która odróżniałaby je od siebie.

Często informacje reprezentowane przez każdy węzeł są rekordem, a nie pojedynczym elementem danych. Jednak do celów sekwencjonowania węzły są porównywane według ich kluczy, a nie jakiejkolwiek części skojarzonych z nimi rekordów. Główną zaletą drzew wyszukiwania binarnego nad innymi strukturami danych jest to, że powiązane algorytmy sortowania i algorytmy wyszukiwania, takie jak przechodzenie w kolejności, mogą być bardzo wydajne.

Drzewa wyszukiwania binarnego są podstawową strukturą danych używaną do konstruowania bardziej abstrakcyjnych struktur danych, takich jak zestawy , multizestawy i tablice asocjacyjne .

Podczas wstawiania lub wyszukiwania elementu w drzewie wyszukiwania binarnego klucz każdego odwiedzanego węzła musi zostać porównany z kluczem elementu, który ma zostać wstawiony lub znaleziony.
Kształt drzewa wyszukiwania binarnego zależy całkowicie od kolejności wstawiania i usuwania i może stać się zdegenerowany.
Po długiej, przemieszanej sekwencji losowego wstawiania i usuwania, oczekiwana wysokość drzewa zbliża się do pierwiastka kwadratowego z liczby kluczy, $\sqrt n$ , która rośnie znacznie szybciej niż $log n$ .
Przeprowadzono wiele badań mających na celu zapobieżenie degeneracji drzewa skutkującej złożonością czasową w najgorszym przypadku $O(n)$ (szczegóły patrz rozdział Typy ).

Zamówienie relacji

Wyszukiwanie binarne wymaga relacji kolejności, dzięki której każdy element (pozycja) może być porównywany z każdym innym elementem w sensie całkowitego zamówienia wstępnego . Część elementu, która efektywnie występuje w porównaniu, nazywana jest jego kluczem . Czy duplikaty, ja. mi. różne elementy z tym samym kluczem, czy mogą być dozwolone w drzewie, czy nie, nie zależy od relacji kolejności, ale od zbioru bazowego, innymi słowy: tylko od aplikacji. Aby zapoznać się z funkcją wyszukiwania obsługującą i obsługującą duplikaty w drzewie, zobacz sekcję Wyszukiwanie z dozwolonymi duplikatami .

W kontekście drzew wyszukiwania binarnego, całkowite zamówienie wstępne jest realizowane najbardziej elastycznie za pomocą podprogramu porównywania trójstronnego .

Operacje

Drzewa wyszukiwania binarnego obsługują trzy główne operacje: wyszukiwanie (sprawdzanie, czy klucz jest obecny), wstawianie elementu i usuwanie elementu. Dwie ostatnie mogą zmienić drzewo, podczas gdy pierwsza jest operacją nawigacyjną i tylko do odczytu. Inne operacje tylko do odczytu to przechodzenie, weryfikacja itp.

Badawczy

Wyszukiwanie określonego klucza w drzewie wyszukiwania binarnego może być programowane rekursywnie lub iteracyjnie .

Zaczynamy od zbadania węzła głównego . Jeśli drzewo ma wartość null , klucz, którego szukamy, nie istnieje w drzewie. W przeciwnym razie, jeśli klucz jest równy kluczowi korzenia, wyszukiwanie się powiedzie i zwracamy węzeł. Jeśli klucz jest mniejszy niż klucz, przeszukujemy lewe poddrzewo. Podobnie, jeśli klucz jest większy niż klucz, przeszukujemy odpowiednie poddrzewo. Ten proces jest powtarzany do momentu znalezienia klucza lub do momentu, gdy pozostałe poddrzewo ma wartość null . Jeśli poszukiwany klucz nie zostanie znaleziony po osiągnięciu zerowego poddrzewa, oznacza to, że klucz nie występuje w drzewie. Można to łatwo wyrazić jako algorytm rekurencyjny (zaimplementowany w Pythonie ):

def search_recursively(key, node):
    if node is None or key == node.key:
        return node
    if key < node.key:
        return search_recursively(key, node.left)
    return search_recursively(key, node.right)

Ten sam algorytm można zaimplementować iteracyjnie:

def search_iteratively(key, node):
    while node is not None and node.key != key:
        if key < node.key:
            node = node.left
        else:
            node = node.right
    return node

Poniższa interaktywna wersja funkcji wyszukiwania nie używa wskaźników nadrzędnych w strukturze danych węzła, zamiast tego używa stosu do przechowywania wskaźników do przodków. Ten stos jest osadzony w większej strukturze, zwanej traverser.

struct TreeNode {
  struct TreeNode *child[2];
  int key;
  int value;
} Node;

#define LEFT  0
#define RIGHT 1
#define left  child[LEFT]
#define right child[RIGHT]

#define MAXheight 1024 // BST is possibly unbalanced

struct traverser {
  Node*  nod1;  // current position (NULL,
                //   if nod1->key ahead or behind all nodes of bst)
  int    dir;   // ∈ {LEFT,FOUND,RIGHT}, i.e.
                // == LEFT  <==> position at < nod1
                // == FOUND <==> position at   nod1
                // == RIGHT <==> position at > nod1
  Node** parent = &ancestors[0]; // -> parent of nod1 or NULL if root
  // ancestors[0] == trav->bst->root, if tree not empty.
  Node** limit  = &ancestors[MAXheight]; // -> utmost entry
  BST*   bst;   // -> BST to which this traverser belongs
  Node*  ancestors[MAXheight-1];
};

// search Iteratively with Traverser:
int searchIT (struct traverser* trav, int key) {
  assert (trav != NULL && trav->bst != NULL);
  trav->parent = &(trav->ancestors[-1]);
  dir = LEFT; // in case trav->bst (and while-loop) is empty
  node = trav->bst->root;
  while (node != NULL) {
    if (key == node->key) { // key is in the BST
      trav->node = node; // onto trav
      trav->dir = FOUND;
      // 2 == FOUND: key == node->key
      return node;
    }
    if (key < node->key) dir = LEFT;
    else dir = RIGHT;
    if (++(trav->parent) >= limit) { // stack overflow
      fprintf (stderr, "tree too deep\n");
      exit (EXIT_FAILURE);
    }
    *(trav->parent) = node; // onto stack
    node = node->child[dir];
  }; // end of while-loop
  // *(trav->parent) is the node of closest fit
  trav->dir = dir;
  // 0 == LEFT:  key < (*(trav->parent))->key
  // 1 == RIGHT: key > (*(trav->parent))->key
  return NULL;
}

Te trzy przykłady nie obsługują duplikatów, to znaczy traktują drzewo jako całkowicie uporządkowane.

Można zauważyć, że algorytm rekurencyjny jest rekurencyjny z ogonem . W języku obsługującym optymalizację funkcji tail call przykłady rekurencyjne i iteracyjne zostaną skompilowane do równoważnych programów.

Ponieważ w najgorszym przypadku ten algorytm musi przeszukiwać od korzenia drzewa do liścia znajdującego się najdalej od korzenia, operacja wyszukiwania zajmuje czas proporcjonalny do wysokości drzewa (patrz terminologia drzewa ). Średnio drzewa wyszukiwania binarnego z kluczami $węzłów$ mają wysokość $O (log | Nodes |)$ . Jednak w najgorszym przypadku drzewa wyszukiwania binarnego mogą mieć wysokość $O(| Nodes |)$ , gdy niezrównoważone drzewo przypomina listę połączoną ( drzewo zdegenerowane ).

Wyszukiwanie z duplikatami dozwolone

Jeśli relacja zamówienia jest tylko całkowitym przedsprzedażą, rozsądnym rozszerzeniem funkcjonalności jest następujące: również w przypadku poszukiwania równości aż do liści. Pozwala to na określenie (lub na stałe) kierunku, w którym należy wstawić duplikat, po prawej lub lewej stronie wszystkich dotychczasowych duplikatów w drzewie. Jeśli kierunek jest ustalony na stałe, obie opcje, prawa i lewa, obsługują stos z wstawianiem duplikatu jako operacją push i usuwaniem jako operacją pop.

def search_duplicatesAllowed(key, node):
    new_node = node
    while new_node != None:
        current_node = new_node
        if key < current_node.key:
            dir = 0  # LEFT
        else:  # key >= current_node.key:
            dir = 1  # RIGHT
        new_node = current_node.child[dir]
    return (dir, current_node)

Binarne drzewo sortowania wyposażony w taką funkcję poprzez poszukiwanie staje się stabilny .

Przemierzanie

Po utworzeniu drzewa wyszukiwania binarnego jego elementy można pobrać w kolejności , przechodząc rekursywnie przez lewe poddrzewo węzła głównego, uzyskując dostęp do samego węzła, a następnie rekursywnie przechodząc przez prawe poddrzewo węzła, kontynuując ten wzorzec z każdym węzłem w drzewie ponieważ jest dostępny rekurencyjnie. Podobnie jak w przypadku wszystkich drzew binarnych, można przeprowadzić przechodzenie przed zamówieniem lub przechodzenie po zamówieniu , ale prawdopodobnie nie będą one przydatne w przypadku drzew wyszukiwania binarnego . Przechodzenie w kolejności w drzewie wyszukiwania binarnego zawsze będzie skutkować posortowaną listą elementów węzłów (liczby, ciągi lub inne porównywalne elementy).

Kod do przechodzenia inorder w Pythonie jest podany poniżej. Wywoła wywołanie zwrotne (niektóre funkcje, które programista chce wywołać na wartości węzła, takie jak drukowanie na ekranie) dla każdego węzła w drzewie.

def inorder_traversal(node, callback):
    if node == None:
        return
    inorder_traversal(node.leftChild, callback)
    callback(node.value)
    inorder_traversal(node.rightChild, callback)

Kod dla (rekursywnego) przechodzenia w kolejności w C jest podany poniżej. W tym przypadku użyje printfdo wydrukowania wartości całkowitej węzła na ekranie.

void inorder_traversal(Node *node) {
  if (node == NULL) return;
  inorder_traversal(node->left);
  printf("%i%i ,", node->key, node->value);
  inorder_traversal(node->right);
}

Każda forma pierwszego przejścia przez głębokość drzewa binarnego wymaga $2\times(n -1) \in O (n)$ czasu, ponieważ odwiedza każdy łuk dokładnie dwa razy (raz w dół, raz w górę) podczas odwiedzania każdego węzła. Ten algorytm to również $O(n)$ , więc jest asymptotycznie optymalny .

Traversal można również zaimplementować iteracyjnie . Dla niektórych aplikacji, np. większe równe wyszukiwanie, wyszukiwanie przybliżone, operacja dlaprzechodzenie jednoetapowe (iteracyjne) może być bardzo przydatne. Jest to oczywiście zaimplementowane bez konstrukcji wywołania zwrotnego.

Przechodzenie do następnego lub poprzedniego węzła

Funkcja ta przydaje się np. w przypadkach, gdy położenie poszukiwanego elementu nie jest wystarczająco dokładnie znane. Po wyszukaniu punktu początkowego wyszukiwanie można kontynuować sekwencyjnie.

Węzeł, który ma zostać uruchomiony, mógł zostać znaleziony w BST za pomocą funkcji wyszukiwania. W poniższym przykładzie, który nie używa wskaźników nadrzędnych, stos wskaźników do przodków został zbudowany np. przez searchITfunkcję z pomyślnym wynikiem.

Funkcja inorderNext zwraca Inorder-sąsiad znaleziony node, albo inorder- Sach cessor (dla dir=RIGHT) lub inorder- prede cessor (za dir=LEFT) i aktualizowana stack, dzięki czemu wyszukiwanie binarne drzewo może być kolejno Inorder-ruch i przeszukane w danym kierunku dirdalej.

/* Returns the next or previous data item in inorder within the tree being traversed with trav, or if there are no more data items returns NULL.
In the former case inorderNext() may be called again to retrieve the second next item. */
Node* inorderNext (struct traverser* trav, dir) {
  assert (trav != NULL);
  assert (trav->dir == FOUND);
  assert (dir == LEFT || dir == RIGHT);

  newnode = trav->node->child[dir];
  if (newnode != NULL) {
// Part A: node has a dir-child.
    do {
      node = newnode;
      if (++(trav->parent) > limit) { // stack overflow
        fprintf (stderr, "tree too deep\n");
        exit (EXIT_FAILURE);
      }
      *(trav->parent) = node; // onto stack
      newnode = node->child[1-dir]
    } until (newnode == NULL);
    return node;
  }
// Part B: node does not have a dir-child.
  do {
    if (--(trav->parent) < &(trav->ancestors[0])) // stack is empty
      return NULL;
    oldnode = node;
    node = *(trav->parent); // parent of oldnode
  } until (oldnode != node->child[dir]);
  // now: oldnode == node->child[1-dir], i.e.
  //      node is ancestor (and predecessor for dir==LEFT resp.
  //      successor for dir==RIGHT) of the original trav->node.
  return node;
}

Zauważ, że funkcja nie używa klawiszy, co oznacza, że sekwencyjna struktura jest całkowicie rejestrowana przez łuki drzewa wyszukiwania binarnego. W przypadku przejść bez zmiany kierunku ( amortyzowana ) średnia złożoność wynika z tego, że pełne przejście zajmuje kroki dla BST o rozmiarze 1 dla łuku w górę i 1 dla łuku w dół. Najgorszy przypadek złożoność jest ze jak wysokość drzewa. ${\mathcal {O}}(1),$ $2n-2$ $n$ ${\ Displaystyle {\ Mathcal {O}} (h)}$ ${\ Displaystyle h}$

Implementacja wymaga przestrzeni stosu proporcjonalnej do wysokości drzewa.

Weryfikacja

Czasami mamy już drzewo binarne i musimy ustalić, czy jest to BST. Ten problem ma proste rozwiązanie rekurencyjne.

Właściwość BST — każdy węzeł w prawym poddrzewie musi być większy niż bieżący węzeł, a każdy węzeł w lewym poddrzewie musi być mniejszy niż bieżący węzeł — jest kluczem do ustalenia, czy drzewo jest BST, czy nie. Algorytm zachłanny -simply przemierzać drzewo, na każdym czeku węzła czy węzeł zawiera wartość większą niż wartość po lewej dziecka i mniejsze niż wartość na prawo dzieci nie działa we wszystkich przypadkach. Rozważ następujące drzewo:

W powyższym drzewie każdy węzeł spełnia warunek, że węzeł zawiera wartość większą niż jego lewy element potomny i mniejszą niż jego prawy element potomny, a mimo to nie jest BST: wartość 5 znajduje się w prawym poddrzewie węzła zawierającego 20 , naruszenie właściwości BST.

Zamiast podejmować decyzje wyłącznie na podstawie wartości węzła i jego dzieci, potrzebujemy również informacji spływających od rodzica. W przypadku powyższego drzewa, gdybyśmy pamiętali o węźle zawierającym wartość 20, zobaczylibyśmy, że węzeł z wartością 5 narusza umowę własności BST.

Tak więc warunek, który musimy sprawdzić w każdym węźle, to:

jeśli węzeł jest lewym dzieckiem swojego rodzica, to musi być mniejszy (lub równy) rodzicowi i musi przekazać wartość ze swojego rodzica do prawego poddrzewa, aby upewnić się, że żaden z węzłów w tym poddrzewie nie jest większy niż rodzic
jeśli węzeł jest prawym dzieckiem swojego rodzica, musi być większy niż rodzic i musi przekazać wartość ze swojego rodzica do lewego poddrzewa, aby upewnić się, że żaden z węzłów w tym poddrzewie nie jest mniejszy od rodzica.

Rozwiązanie rekurencyjne w C++ może to wyjaśnić dalej:

struct TreeNode {
    int key;
    int value;
    struct TreeNode *left;
    struct TreeNode *right;
};

bool isBST(struct TreeNode *node, int minKey, int maxKey) {
    if (node == NULL) return true;
    if (node->key < minKey || node->key > maxKey) return false;
    
    return isBST(node->left, minKey, node->key−1) && isBST(node->right, node->key+1, maxKey);
}

node->key+1i node->key−1są zrobione, aby umożliwić tylko odrębne elementy w BST.

Jeśli chcemy, aby te same elementy również były obecne, możemy użyć tylko node->keyw obu miejscach.

Początkowe wywołanie tej funkcji może wyglądać mniej więcej tak:

if (isBST(root, INT_MIN, INT_MAX)) {
    puts("This is a BST.");
} else {
    puts("This is NOT a BST!");
}

Zasadniczo tworzymy poprawny zakres (zaczynając od [MIN_VALUE, MAX_VALUE]) i zmniejszamy go dla każdego węzła w miarę zmniejszania się rekurencyjnie.

Jak wskazano w sekcji #Traversal , przechodzenie inorder w drzewie wyszukiwania binarnego zwraca posortowane węzły. Dlatego wystarczy zachować ostatni odwiedzony węzeł podczas przemierzania drzewa i sprawdzić, czy jego klucz jest mniejszy (lub mniejszy/równy, jeśli w drzewie mają być dozwolone duplikaty) w porównaniu z bieżącym kluczem.

Wprowadzenie

Wstawianie rozpoczyna się tak, jak rozpoczęłoby się wyszukiwanie; jeśli klucz nie jest równy kluczowi korzenia, przeszukujemy lewe lub prawe poddrzewa tak jak poprzednio. W końcu dotrzemy do zewnętrznego węzła i dodamy nową parę klucz-wartość (tutaj zakodowaną jako rekord 'newNode') jako jego prawy lub lewy element potomny, w zależności od klucza węzła. Innymi słowy, sprawdzamy korzeń i rekurencyjnie wstawiamy nowy węzeł do lewego poddrzewa, jeśli jego klucz jest mniejszy niż klucz korzenia, lub do prawego poddrzewa, jeśli jego klucz jest większy lub równy korzeniowi.

Oto jak można wykonać typowe wstawianie drzewa wyszukiwania binarnego w drzewie binarnym w C++ :

void insert(Node*& root, int key, int value) {
  if (!root) 
    root = new Node(key, value);
  else if (key == root->key)
    root->value = value;
  else if (key < root->key)
    insert(root->left, key, value);
  else  // key > root->key
    insert(root->right, key, value);
}

Alternatywnie, nierekurencyjna wersja może być zaimplementowana w C w ten sposób. Używanie wskaźnika do wskaźnika do śledzenia, skąd pochodzimy, pozwala kodowi uniknąć jawnego sprawdzania i obsługi sprawy, w której musi wstawić węzeł w korzeniu drzewa:

void insert(Node** root, int key, int value) {
  Node **walk = root;
  while (*walk) { 
    int curkey = (*walk)->key;
    if (curkey == key) {
      (*walk)->value = value;
      return;
    }
    if (key > curkey) 
      walk = &(*walk)->right;
    else 
      walk = &(*walk)->left;
  }
  *walk = new Node(key, value);
}

W poniższym przykładzie, który nie używa wskaźników nadrzędnych, stos wskaźników do przodków został zbudowany np. przez searchITfunkcję z kluczem wyniku node->keynot FOUND.

// insert after search Iteratively with Traverser:
void insertIT(struct traverser* trav,Node* node) {
  assert (trav != NULL);
  assert (trav->node != NULL);
  assert (trav->dir == LEFT || trav->dir == RIGHT);
  assert (node != NULL);
  trav->node->child[trav->dir] = node;
  if (++(trav->parent) > limit) { // stack overflow
    fprintf (stderr, "tree too deep\n");
    exit (EXIT_FAILURE);
  }
  *(trav->parent) = node; // onto stack
}

Powyższy destrukcyjny wariant proceduralny modyfikuje drzewo w miejscu. Używa tylko stałej przestrzeni stosu (a wersja iteracyjna również używa stałej przestrzeni stosu), ale poprzednia wersja drzewa jest tracona. Alternatywnie, jak w poniższym przykładzie Pythona , możemy zrekonstruować wszystkich przodków wstawionego węzła; wszelkie odniesienia do oryginalnego korzenia drzewa pozostają ważne, dzięki czemu drzewo jest trwałą strukturą danych :

def binary_tree_insert(node, key, value):
    if node == None:
        return NodeTree(None, key, value, None)
    if key == node.key:
        return NodeTree(node.left, key, value, node.right)
    if key < node.key:
        return NodeTree(binary_tree_insert(node.left, key, value), node.key, node.value, node.right)
    return NodeTree(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))

Odbudowana część wykorzystuje przestrzeń $O (log n)$ w przeciętnym przypadku i $O(n)$ w najgorszym przypadku.

W obu wersjach operacja ta wymaga czasu proporcjonalnego do wysokości drzewa w najgorszym przypadku, czyli czasu $O(log n)$ w średnim przypadku nad wszystkimi drzewami, ale czasu $O(n)$ w najgorszym przypadku.

Innym sposobem wyjaśnienia wstawiania jest to, że aby wstawić nowy węzeł do drzewa, jego klucz jest najpierw porównywany z kluczem korzenia. Jeśli jego klucz jest mniejszy niż klucz korzenia, jest on następnie porównywany z kluczem lewego dziecka korzenia. Jeśli jego klucz jest większy, jest porównywany z prawym dzieckiem korzenia. Proces ten trwa, dopóki nowy węzeł nie zostanie porównany z węzłem liścia, a następnie zostanie dodany jako prawy lub lewy element potomny tego węzła, w zależności od jego klucza: jeśli klucz jest mniejszy niż klucz liścia, to jest on wstawiany jako klucz liścia lewe dziecko, inaczej jak prawe dziecko liścia.

Istnieją inne sposoby wstawiania węzłów do drzewa binarnego, ale jest to jedyny sposób wstawiania węzłów przy liściach przy jednoczesnym zachowaniu struktury BST.

Usunięcie

Podczas usuwania węzła z drzewa wyszukiwania binarnego obowiązkowe jest zachowanie kolejności węzłów. Jest na to wiele możliwości. Jednak następująca metoda, zaproponowana przez T. Hibbarda w 1962 r., gwarantuje, że wysokości poddrzew przedmiotowych zmieniają się co najwyżej o jeden. Istnieją trzy możliwe przypadki do rozważenia:

Usuwanie węzła bez dzieci: po prostu usuń węzeł z drzewa.
Usuwanie węzła z jednym dzieckiem: usuń węzeł i zastąp go jego dzieckiem.
Usuwanie węzła D z dwójką dzieci: wybierz poprzednika w kolejności D lub następcę E w kolejności (patrz rysunek). Zamiast usuwać D , nadpisz jego klucz i wartość literami E . Jeśli E nie ma dziecka, usuń E z poprzedniego rodzica G ; jeśli E ma dziecko F , jest to właściwe dziecko, więc ma zastąpić E w G .

Usuwanie węzła D z dwójką dzieci z drzewa wyszukiwania binarnego. Najpierw identyfikowany jest skrajny lewy węzeł w prawym poddrzewie, następca w kolejności E . Jego wartość jest kopiowana do węzła D usunięciem. Następca kolejności można łatwo usunąć, ponieważ ma co najwyżej jedno dziecko (które w ogólnym niezrównoważonym przypadku może być poddrzewem).
Ta sama metoda działa symetrycznie przy użyciu poprzednika inorder C .

We wszystkich przypadkach, gdy D jest korzeniem, ponownie utwórz zastępczy korzeń węzła.

Węzły z dwójką dzieci (przypadek 3) są trudniejsze do usunięcia (patrz rysunek). Następca węzła D w kolejności jest najbardziej lewym dzieckiem jego prawego poddrzewa, powiedzmy E , a poprzednikiem węzła w kolejności jest najbardziej prawe dziecko lewego poddrzewa, powiedzmy C. W obu przypadkach, taki węzeł E lub C nie będzie miał lewego lub odpowiednio. prawe dziecko, więc można je usunąć zgodnie z jednym z dwóch prostszych przypadków 1 lub 2 powyżej.

Konsekwentne używanie następnika inorder lub poprzednika inorder dla każdej instancji przypadku z dwoma podrzędnymi może prowadzić do niezrównoważonego drzewa, więc niektóre implementacje wybierają jedno lub drugie w różnym czasie.

Analiza w czasie wykonywania: chociaż ta operacja nie zawsze przechodzi przez drzewo aż do liścia, zawsze jest to możliwe; zatem w najgorszym przypadku wymaga czasu proporcjonalnego do wysokości drzewa. Nie wymaga więcej, nawet gdy węzeł ma dwoje dzieci, ponieważ nadal podąża jedną ścieżką i nie odwiedza żadnego węzła dwukrotnie.

def find_min(self):
    """Get minimum node in a subtree."""
    current_node = self
    while current_node.left_child:
        current_node = current_node.left_child
    return current_node

def replace_node_in_parent(self, new_value=None) -> None:
    if self.parent:
        if self == self.parent.left_child:
            self.parent.left_child = new_value
        else:
            self.parent.right_child = new_value
    if new_value:
        new_value.parent = self.parent

def binary_tree_delete(self, key) -> None:
    if key < self.key:
        self.left_child.binary_tree_delete(key)
        return
    if key > self.key:
        self.right_child.binary_tree_delete(key)
        return
    # Delete the key here
    if self.left_child and self.right_child:  # If both children are present
        successor = self.right_child.find_min()
        self.key = successor.key
        successor.binary_tree_delete(successor.key)
    elif self.left_child:  # If the node has only a *left* child
        self.replace_node_in_parent(self.left_child)
    elif self.right_child:  # If the node has only a *right* child
        self.replace_node_in_parent(self.right_child)
    else:
        self.replace_node_in_parent(None)  # This node has no children

Algorytmy równoległe

Istnieje również równoległe algorytmy binarnego drzewa wyszukiwania oraz wprowadzania / usuwania wielu elementów budowlanych, z tablicy, filtr z pewnymi predicator, spłaszczyć do tablicy połączenia / odjęcie / przecinającą dwóch drzew itp algorytmy te mogą być realizowane za pomocą przyłączenia oparte algorytmy drzew , które mogą mieć także drzew wyważane kilka schematów równoważenia (w tym AVL drzewa , czerwono-czarny drzewa , drzewa wagowo zrównoważone i treap ).

Przykłady zastosowań

Sortować

Drzewo wyszukiwania binarnego może być użyte do zaimplementowania prostego algorytmu sortowania . Podobnie jak w przypadku heapsort , wstawiamy wszystkie wartości, które chcemy posortować, do nowej uporządkowanej struktury danych — w tym przypadku binarnego drzewa wyszukiwania — a następnie przeszukujemy je w kolejności.

Najgorszy przypadek build_binary_treeto $O(n 2) —$ jeśli nadasz mu posortowaną listę wartości, połączy je w połączoną listę bez lewych poddrzew. Na przykład build_binary_tree([1, 2, 3, 4, 5])daje drzewo (1 (2 (3 (4 (5))))).

Istnieje kilka sposobów na pokonanie tej wady za pomocą prostych drzew binarnych; najczęstszym jest samobalansujące drzewo wyszukiwania binarnego . Jeśli ta sama procedura jest wykonywana przy użyciu takiego drzewa, całkowity czas najgorszego przypadku wynosi $O(n log n)$ , co jest asymptotycznie optymalne dla sortowania porównawczego . W praktyce dodatkowy narzut w czasie i przestrzeni dla sortowania opartego na drzewie (szczególnie w przypadku alokacji węzłów ) czyni go gorszym od innych asymptotycznie optymalnych sortowań, takich jak sortowanie sterty do statycznego sortowania list. Z drugiej strony jest to jedna z najskuteczniejszych metod sortowania przyrostowego , polegająca na dodawaniu elementów do listy w miarę upływu czasu przy jednoczesnym utrzymaniu listy posortowanej przez cały czas.

Operacje w kolejce priorytetowej

Drzewa wyszukiwania binarnego mogą służyć jako kolejki priorytetowe : struktury umożliwiające wstawianie dowolnego klucza oraz wyszukiwanie i usuwanie klucza minimalnego (lub maksymalnego). Wstawianie działa tak, jak wyjaśniono wcześniej. Find-min chodzi po drzewie, podążając za lewymi wskazówkami tak daleko, jak to możliwe, nie uderzając w liść:

// Precondition: T is not a leaf
function find-min(T):
    while hasLeft(T):
        T ? left(T)
    return key(T)

Find-max jest analogiczny: podążaj za prawymi wskazówkami tak daleko, jak to możliwe. Delete-min ( max ) może po prostu wyszukać minimum (maksimum), a następnie je usunąć. W ten sposób zarówno wstawianie, jak i usuwanie zajmuje czas logarytmiczny, tak jak w stercie binarnej , ale w przeciwieństwie do sterty binarnej i większości innych implementacji kolejek priorytetowych, jedno drzewo może obsługiwać wszystkie find-min , find-max , delete-min i delete-max w tym samym czasie, dzięki czemu drzewa wyszukiwania binarnego są odpowiednie jako podwójnie zakończone kolejki priorytetowe .

Rodzaje

Istnieje wiele rodzajów drzew wyszukiwania binarnego. Drzewa AVL i czerwono-czarne są formami samobalansujących się drzew binarnych . Drzewo splay to drzewo binarne wyszukiwania, które automatycznie przenosi często używanych elementów bliżej korzenia. W treap ( sterta drzewa ) każdy węzeł posiada również (losowo wybrany) priorytet, a węzeł nadrzędny ma wyższy priorytet niż jego dzieci. Drzewa tanga to drzewa zoptymalizowane pod kątem szybkiego wyszukiwania. T-drzewa to drzewa wyszukiwania binarnego zoptymalizowane pod kątem zmniejszenia obciążenia pamięci masowej, szeroko stosowane w bazach danych w pamięci

Drzewo zdegenerowane to drzewo, w którym dla każdego węzła nadrzędnego istnieje tylko jeden skojarzony węzeł podrzędny. Jest niezrównoważony i, w najgorszym przypadku, wydajność spada do listy połączonej. Jeśli funkcja dodawania węzła nie obsługuje ponownego równoważenia, możesz łatwo zbudować zdegenerowane drzewo, zasilając je danymi, które są już posortowane. Oznacza to, że w pomiarze wydajności drzewo będzie zasadniczo zachowywać się jak połączona struktura danych listy.

Porównania wydajności

DA Heger (2004) przedstawił porównanie wydajności drzew wyszukiwania binarnego. Stwierdzono, że Treap ma najlepszą średnią wydajność, podczas gdy czerwono-czarne drzewo ma najmniejszą liczbę zmian wydajności.

Optymalne drzewa wyszukiwania binarnego

Rotacje drzew są bardzo powszechnymi operacjami wewnętrznymi w drzewach binarnych, które mają na celu utrzymanie idealnej lub prawie idealnej wewnętrznej równowagi w drzewie.

Jeśli drzewo wyszukiwania nie jest przeznaczone do modyfikacji i wiadomo dokładnie, jak często każdy element będzie dostępny, możliwe jest skonstruowanie optymalnego drzewa wyszukiwania binarnego , które jest drzewem wyszukiwania, w którym średni koszt wyszukiwania elementu ( spodziewany koszt wyszukiwania ) jest zminimalizowane.

Nawet jeśli mamy tylko szacunki kosztów wyszukiwania, taki system może średnio znacznie przyspieszyć wyszukiwanie. Na przykład, jeśli mamy BST angielskich słów używanych w sprawdzania pisowni , możemy zrównoważyć drzewa w oparciu o częstotliwość występowania słów w korpusach tekstu , umieszczając słowa jak blisko korzenia i słowami jak agerasia blisko liści. Takie drzewo można porównać z drzewami Huffmana , które podobnie starają się umieszczać często używane elementy w pobliżu korzenia, aby uzyskać gęste kodowanie informacji; jednak drzewa Huffmana przechowują elementy danych tylko w liściach i nie trzeba ich porządkować.

Jeśli sekwencja, w której elementy w drzewie będą dostępne, jest z góry nieznana, można użyć drzew splay , które są asymptotycznie tak dobre, jak każde statyczne drzewo wyszukiwania, które możemy skonstruować dla dowolnej sekwencji operacji wyszukiwania.

Drzewa alfabetyczne to drzewa Huffmana z dodatkowym ograniczeniem kolejności lub równoważnie drzewa wyszukiwania z tą modyfikacją, że wszystkie elementy są przechowywane w liściach. Istnieją szybsze algorytmy dla optymalnych alfabetycznych drzew binarnych (OABT).

Zobacz też

Uwagi

Bibliografia

Dalsza lektura

Ten artykuł zawiera materiał z domeny publicznej z dokumentu NIST : Black, Paul E. „Drzewo wyszukiwania binarnego” . Słownik algorytmów i struktur danych .
Cormen, Thomas H .; Leiserson, Charles E. ; Rivest, Ronald L .; Stein, Clifford (2001). „12: Binarne drzewa wyszukiwania, 15.5: Optymalne binarne drzewa wyszukiwania”. Wprowadzenie do algorytmów (wyd. 2). MIT Press i McGraw-Hill. s. 253–272, 356–363. Numer ISBN 0-262-03293-7.
Jarc, Duane J. (3 grudnia 2005). „Przejścia przez drzewa binarne” . Interaktywne wizualizacje struktury danych . Uniwersytet Maryland . Zarchiwizowane z oryginału w dniu 27 lutego 2014 r . Pobrano 30 kwietnia 2006 .
Knut, Donald (1997). „6.2.2: Wyszukiwanie drzewa binarnego”. Sztuka Programowania Komputerowego . 3: „Sortowanie i wyszukiwanie” (3rd ed.). Addisona-Wesleya. s. 426-458. Numer ISBN 0-201-89685-0.
Długi, Sean. "Drzewo wyszukiwania binarnego" ( PPT ) . Struktury danych i algorytmy Wizualizacja — podejście oparte na slajdach PowerPoint . SUNY Oneonta .
Parlante, Nick (2001). „Drzewa binarne” . Biblioteka edukacyjna CS . Uniwersytet Stanforda .

Zewnętrzne linki

Ben Pfaff: Wprowadzenie do binarnych drzew wyszukiwania i zrównoważonych drzew . (PDF; 1675 kB) 2004.
Wizualizator drzewa binarnego (animacja JavaScript różnych struktur danych opartych na BT)

Languages

In other projects