Wykres kaktusowy - Cactus graph
W teorii wykres , A kaktus (czasami nazywany drzewa kaktus ) jest połączony wykres , w którym dowolne dwa proste cykli co najwyżej jednego wierzchołka wspólne. Równoważnie jest to graf spójny, w którym każda krawędź należy do co najwyżej jednego prostego cyklu lub (dla nietrywialnych kaktusów), w którym każdy blok (maksymalny podgraf bez wierzchołka tnącego ) jest krawędzią lub cyklem.
Nieruchomości
Kaktusy to grafy zewnętrzne . Każde pseudodrzewo to kaktus. Nietrywialny wykres to kaktus wtedy i tylko wtedy, gdy każdy blok jest albo prostym cyklem, albo pojedynczą krawędzią.
Rodzina grafów, w której każdy składnik jest kaktusem, jest zamknięta w dół w ramach mniejszych operacji grafu . Ta rodzina grafów może charakteryzować się pojedynczym zabronionym molem , czterowierzchołkowym grafem rombowym utworzonym przez usunięcie krawędzi z pełnego grafu K 4 .
Kaktus trójkątny
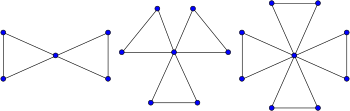
Kaktus trójkątny to specjalny rodzaj grafu kaktusa, w którym każdy cykl ma długość trzy, a każda krawędź należy do cyklu. Na przykład grafy przyjaźni , grafy utworzone ze zbioru trójkątów połączonych ze sobą na jednym wspólnym wierzchołku, są trójkątnymi kaktusami. Oprócz tego, że są grafami kaktusowymi, trójkątne kaktusy są również grafami blokowymi i grafami lokalnie liniowymi .
Kaktusy trójkątne mają tę właściwość, że pozostają połączone, jeśli usunie się z nich jakiekolwiek dopasowanie ; dla danej liczby wierzchołków mają najmniejszą możliwą liczbę krawędzi z tą właściwością. Każde drzewo o nieparzystej liczbie wierzchołków może być augmentowane do trójkątnego kaktusa poprzez dodanie do niego krawędzi, dając minimalną augmentację z właściwością pozostania połączonym po usunięciu dopasowania.
Największy trójkątny kaktus na dowolnym wykresie można znaleźć w czasie wielomianowym przy użyciu algorytmu problemu parzystości matroidalnej . Ponieważ trójkątne grafy kaktusowe są grafami planarnymi , największy trójkątny kaktus może być używany jako przybliżenie największego płaskiego podgrafu, co jest ważnym podproblemem w planaryzacji . Jako algorytm aproksymacyjny , metoda ta ma współczynnik aproksymacji 4/9, najlepiej znany z problemu podgrafu maksymalnego płaskiego.
Algorytm znajdowania największego trójkątnego kaktusa jest powiązany z twierdzeniem Lovásza i Plummera, które charakteryzuje liczbę trójkątów w tym największym kaktusie. Lovász i Plummer rozważają pary podziałów wierzchołków i krawędzi danego grafu na podzbiory, z tą właściwością, że każdy trójkąt grafu ma albo dwa wierzchołki w jednej klasie podziału wierzchołków, albo wszystkie trzy krawędzie w jednej klasie przegroda krawędziowa; nazywają parę partycji z tą właściwością valid . Wtedy liczba trójkątów w największym trójkątnym kaktusie jest równa maksimum, w parach prawidłowych przegród i , z
- ,
gdzie jest liczbą wierzchołków w danym grafie i jest liczbą klas wierzchołków spełnianych przez klasę krawędzi .
Ostatnio udowodniono ścisłe ograniczenie ekstremalne, które wykazało, że przy dowolnym wykresie płaskim zawsze istnieje podgraf kaktusowy zawierający przynajmniej ułamek trójkątnych ścian . Wynik ten implikuje bezpośrednią analizę algorytmu 4/9 - aproksymacji dla problemu maksymalnego podgrafu płaskiego bez użycia powyższego wzoru min-max.
Przypuszczenie Rosy
Ważną hipotezą związaną z trójkątnym kaktusem jest Hipoteza Rosy , nazwana na cześć Aleksandra Rosy , która mówi, że wszystkie trójkątne kaktusy są pełne wdzięku lub prawie pełne wdzięku. Dokładniej
Wszystkie trójkątne kaktusy z blokami t ≡ 0, 1 mod 4 są pełne wdzięku, a te z t ≡ 2, 3 mod 4 są bliskie wdzięku.
Algorytmy i aplikacje
Niektóre problemy z lokalizacją obiektu, które są NP-trudne dla grafów ogólnych, a także inne problemy z grafami, można rozwiązać w czasie wielomianowym dla kaktusów.
Ponieważ kaktusy są szczególnymi przypadkami grafów zewnętrznych , wiele problemów optymalizacji kombinatorycznej na grafach można dla nich rozwiązać w czasie wielomianowym .
Kaktusy reprezentują obwody elektryczne, które mają użyteczne właściwości. Wczesne zastosowanie kaktusów wiązało się z reprezentacją wzmacniaczy operacyjnych.
Kaktusy są również ostatnio wykorzystywane w genomice porównawczej jako sposób przedstawiania relacji między różnymi genomami lub częściami genomów.
Jeśli kaktus jest połączony, a każdy z jego wierzchołków należy do co najwyżej dwóch bloków, nazywa się go kaktusem bożonarodzeniowym . Każdy graf wielościenny ma podgraf kaktusa bożonarodzeniowego, który zawiera wszystkie jego wierzchołki, co odgrywa istotną rolę w dowodzie Leightona i Moitry (2010), że każdy graf wielościenny ma zachłanne osadzenie w płaszczyźnie euklidesowej , przypisanie współrzędnych do wierzchołki, dla których zachłanne przekazywanie udaje się kierować wiadomościami między wszystkimi parami wierzchołków.
W topologicznej teorii grafów grafy, których osadzenia komórkowe są wszystkie płaskie, są dokładnie podrodziną grafów kaktusowych z dodatkową właściwością, do której każdy wierzchołek należy co najwyżej w jednym cyklu. Te wykresy mają dwa zakazane niepełne, wykres diamentowy i wykres przyjaźni z pięcioma wierzchołkami .
Historia
Kaktusy były po raz pierwszy badane pod nazwą drzew Husimi , nadaną im przez Franka Harary'ego i George'a Eugene'a Uhlenbecka na cześć wcześniejszej pracy nad tymi wykresami przez Kôdiego Husimi . Ten sam artykuł Harary'ego-Uhlenbecka zastrzega sobie nazwę „kaktus” dla wykresów tego typu, w których każdy cykl jest trójkątem, ale teraz dopuszczanie cykli o dowolnej długości jest standardem.
Tymczasem nazwa drzewo Husimi powszechnie odnosiła się do grafów, w których każdy blok jest grafem kompletnym (odpowiednik grafów przecięcia bloków w innym grafie). To użycie miało niewiele wspólnego z pracą Husimi, a bardziej trafny wykres blokowy terminów jest teraz używany dla tej rodziny; jednak z powodu tej niejednoznaczności wyrażenie to stało się rzadziej używane w odniesieniu do wykresów kaktusowych.










