Rektyfikowane 24-ogniwowe - Rectified 24-cell

Rektyfikowana 24-komorowa
Schemat Schlegela 8 z 24 pokazanymi komórkami sześciennymi
Rodzaj	Jednolity 4-polytope
Symbole Schläfliego	r {3,4,3} = rr {3,3,4} = r {3 1,1,1 } = ${\ Displaystyle \ lewo \ {{\ początek {tablica} {l} 3 \\ 4,3 \ koniec {tablica}} \ prawo \}}$ ${\ Displaystyle r \ lewo \ {{\ początek {tablica} {l} 3 \\ 3,4 \ koniec {tablica}} \ prawo \}}$ ${\ Displaystyle r \ lewo \ {{\ początek {tablica} {l} 3 \\ 3 \\ 3 \ koniec {tablica}} \ prawo \}}$
Diagramy Coxetera	lub
Komórki	48	24 3.4.3.4 24 4.4.4
Twarze	240	96 {3} 144 {4}
Krawędzie	288
Wierzchołki	96
Figura wierzchołka	Trójkątny pryzmat
Grupy symetrii	F 4 [3,4,3], rząd 1152 B 4 [3,3,4], rząd 384 D 4 [3 1,1,1 ], rząd 192
Nieruchomości	wypukłe , przechodnie od krawędzi
Jednolity indeks	22 23 24

W geometrii The usunięte 24-komórka lub naprawione icositetrachoron jest jednolity Polytope 4-wymiarową (lub jednolite 4-Polytope ), który jest ograniczony przez 48 komórek : 24 kostki i 24 cuboctahedra . Można go uzyskać poprzez rektyfikację 24-ogniwowego, redukując jego oktaedryczne komórki do kostek i kuboktaedrów.

EL Elte zidentyfikował go w 1912 roku jako półregularny polytop, oznaczając go jako tC ₂₄ .

Można go również uznać za kantelowany 16-ogniwowy o niższych symetriach B ₄ = [3,3,4]. B ₄ doprowadziłyby do bicoloring z cuboctahedral komórek do 8 i 16 każdy. Nazywa się go również runcicantellated demitesseract w symetrii D ₄ , co daje 3 kolory komórek, po 8 dla każdego.

Budowa

Rektyfikowane 24-ogniwa można uzyskać z 24-ogniwowego procesu rektyfikacji : 24-ogniwowe jest obcięte w środkowych punktach. Wierzchołki stają się sześcianami , podczas gdy ośmiościany stają się kuboktaedrami .

współrzędne kartezjańskie

Prostowana 24-komórkowa komórka o długości krawędzi √ 2 ma wierzchołki określone przez wszystkie permutacje i permutacje znaku następujących współrzędnych kartezjańskich :

(0,1,1,2) [4! / 2! × 2 ³ = 96 wierzchołków]

Konfiguracja podwójna z długością krawędzi 2 ma wszystkie permutacje współrzędnych i znaków:

(0,2,2,2) [4 × 2 ³ = 32 wierzchołki]

(1,1,1,3) [4 × 2 ⁴ = 64 wierzchołki]

Obrazy

rzuty ortograficzne

Samolot Coxetera	F 4
Wykres
Symetria dwuścienna	[12]
Samolot Coxetera	B 3 / A 2 (a)	B 3 / A 2 (b)
Wykres
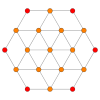
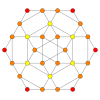
Symetria dwuścienna	[6]	[6]
Samolot Coxetera	B 4	B 2 / A 3
Wykres
Symetria dwuścienna	[8]	[4]

Projekcja stereograficzna
Środek projekcji stereograficznej z 96 trójkątnymi ścianami w kolorze niebieskim

Konstrukcje symetryczne

Istnieją trzy różne konstrukcje symetrii tego polytope'a. Najniższą konstrukcję można podwoić , dodając lustro, które odwzorowuje wzajemnie rozwidlające się węzły. można odwzorować do symetrii, dodając dwa lustra, które odwzorowują wszystkie trzy węzły końcowe razem. ${\ displaystyle {D} _ {4}}$${\ displaystyle {C} _ {4}}$${\ displaystyle {D} _ {4}}$${\ displaystyle {F} _ {4}}$

Postać wierzchołek jest trójkątny graniastosłupa , składający się z dwóch modułów, a trzy cuboctahedra. Te trzy symetrie można zobaczyć z 3 kolorowymi kuboktaedrami w najniższej konstrukcji i dwoma kolorami (stosunek 1: 2) w , a wszystkie identyczne kuboktaedry w . ${\ displaystyle {D} _ {4}}$${\ displaystyle {C} _ {4}}$${\ displaystyle {F} _ {4}}$

Grupa Coxetera	${\ displaystyle {F} _ {4}}$ = [3,4,3]	${\ displaystyle {C} _ {4}}$ = [4,3,3]	${\ displaystyle {D} _ {4}}$ = [3,3 1,1 ]
Zamówienie	1152	384	192
Pełna grupa symetrii	[3,4,3]	[4,3,3]	<[3,3 1,1 ]> = [4,3,3] [3 [3 1,1,1 ]] = [3,4,3]
Diagram Coxetera
Aspekty	3: 2:	2,2: 2:	1,1,1: 2:
Figura wierzchołka

Nazwy alternatywne

• Rektyfikowane 24-ogniwowe, Cantellated 16-ogniwowe ( Norman Johnson )
• Rectified icositetrachoron (akronim rico) (George Olshevsky, Jonathan Bowers)
  • Cantellated hexadecachoron
• Disicositetrachoron
• Amboicositetrachoron ( Neil Sloane & John Horton Conway )

Powiązane polytopy

Wypukły kadłub rektyfikowanej 24-ogniwowej komórki i jej podwójny (zakładając, że są przystające) jest niejednorodnym polichoronem złożonym z 192 komórek: 48 sześcianów , 144 kwadratowych antypryzmatów i 192 wierzchołków. Jego kształt wierzchołkowy to trójkątny bifrustum .

Powiązane jednolite polytopy

D 4 jednolita polichora
{3,3 1,1 } h {4,3,3}	2r {3,3 1,1 } h 3 {4,3,3}	t {3,3 1,1 } h 2 {4,3,3}	2t {3,3 1,1 } h 2,3 {4,3,3}	r {3,3 1,1 } {3 1,1,1 } = {3,4,3}	rr {3,3 1,1 } r {3 1,1,1 } = r {3,4,3}	tr {3,3 1,1 } t {3 1,1,1 } = t {3,4,3}	sr {3,3 1,1 } s {3 1,1,1 } = s {3,4,3}

24-komórkowe polytopy rodzinne
Nazwa	24 ogniwa	obcięty 24-komorowy	snub 24-ogniwowy	rektyfikowane 24-ogniwowe	kantelowany 24-komorowy	bitruncated 24 komórki	cantitruncated 24-komorowy	runcynowany 24-komorowy	runcitruncated 24-komorowy	omnitruncated 24-komorowy
Symbol Schläfli	{3,4,3}	t 0,1 {3,4,3} t {3,4,3}	s {3,4,3}	t 1 {3,4,3} r {3,4,3}	t 0,2 {3,4,3} rr {3,4,3}	t 1,2 {3,4,3} 2t {3,4,3}	t 0,1,2 {3,4,3} tr {3,4,3}	t 0,3 {3,4,3}	t 0,1,3 {3,4,3}	t 0,1,2,3 {3,4,3}
Diagram Coxetera
Diagram Schlegla
F 4
B 4
B 3 (a)
B 3 b)
B 2

Usunięte 24 komórek można również otrzymać jako cantellated 16 komórek :

Polytopy symetrii B4
Nazwa	tesseract	rektyfikowany tesserakt	obcięty tesseract	kantelowany tesserakt	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Diagram Coxetera		=				=
Symbol Schläfli	{4,3,3}	t 1 {4,3,3} r {4,3,3}	t 0,1 {4,3,3} t {4,3,3}	t 0,2 {4,3,3} rr {4,3,3}	t 0,3 {4,3,3}	t 1,2 {4,3,3} 2t {4,3,3}	t 0,1,2 {4,3,3} tr {4,3,3}	t 0,1,3 {4,3,3}	t 0,1,2,3 {4,3,3}
Diagram Schlegla
B 4
Nazwa	16 ogniw	rektyfikowane 16-ogniwowe	obcięty 16-komorowy	kantelowana 16-komorowa	runcinated 16-komorowy	bitruncated 16 komórek	niecięty 16-komorowy	runcitruncated 16-komorowy	omnitruncated 16-komorowy
Diagram Coxetera	=	=	=	=		=	=
Symbol Schläfli	{3,3,4}	t 1 {3,3,4} r {3,3,4}	t 0,1 {3,3,4} t {3,3,4}	t 0,2 {3,3,4} rr {3,3,4}	t 0,3 {3,3,4}	t 1,2 {3,3,4} 2t {3,3,4}	t 0,1,2 {3,3,4} tr {3,3,4}	t 0,1,3 {3,3,4}	t 0,1,2,3 {3,3,4}
Diagram Schlegla
B 4

Cytaty

Bibliografia

• T. Gosset : On the Regular and Semi-Regular Figures in Space of n Dimensions , Messenger of Mathematics, Macmillan, 1900
• Coxeter, HSM (1973) [1948]. Regular Polytopes (3rd ed.). Nowy Jork: Dover.
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN   978-1-56881-220-5 (Rozdział 26. str. 409: Hemicubes: 1 _n1 )
• Norman Johnson Uniform Polytopes , rękopis (1991)
  • NW Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
• 2. Wypukła jednorodna polichora oparta na tesserakcie (8 komórek) i heksadekachoronie (16 komórek) - Model 23 , George Olshevsky.
  • 3. Wypukła jednorodna polichora oparta na icositetrachoron (24-komorowa) - Model 23 , George Olshevsky.
  • 7. Jednolita polichora pochodząca z czworościanu kłębuszkowego B4 - Model 23 , George Olshevsky.
• Klitzing, Richard. „Jednolite polytopy 4D (polychora) o3x4o3o - rico” .

v t mi Zasadnicze wypukłe regularne i jednolite polytopy o wymiarach 2–10
Rodzina	A n	B n	I 2 (p) / D n	E 6 / E 7 / E 8 / F 4 / G 2	H n
Regularny wielokąt	Trójkąt	Plac	p-gon	Sześciokąt	Pięciokąt
Jednolity wielościan	Czworościan	Ośmiościan • Sześcian	Demicube		Dwunastościan • Icosahedron
Jednolity 4-polytope	5-komorowa	16-ogniwowy • Tesseract	Demitesseract	24 ogniwa	120 ogniw • 600 ogniw
Jednolity 5-polytope	5-simplex	5-ortoplex • 5-kostka	5-demicube
Jednolity 6-polytope	6-simplex	6-ortoplex • 6-cube	6-demicube	1 22 • 2 21
Jednolity 7-polytope	7-simplex	7-ortoplex • 7-kostka	7-demicube	1 32 • 2 31 • 3 21
Jednolity 8-polytope	8-simplex	8-ortoplex • 8-kostka	8-demicube	1 42 • 2 41 • 4 21
Jednolity 9-polytope	9-simplex	9-ortoplex • 9-kostka	9-demicube
Jednolity 10-polytope	10-simplex	10-ortoplex • 10-kostka	10-demicube
Jednolity n - polytope	n - simplex	n - ortopleks • n - sześcian	n - demicube	1 k2 • 2 k1 • k 21	n - pięciokątny polytope
Tematy: Rodziny polytopów • Regularne polytopy • Lista regularnych polytopów i związków