Krata Bravais - Bravais lattice

W geometrii i krystalografii , sieć Bravais , nazwana na cześć Auguste Bravais ( 1850 ), jest nieskończoną tablicą dyskretnych punktów generowanych przez zestaw dyskretnych operacji translacji opisanych w przestrzeni trójwymiarowej przez:

\mathbf {R} =n_{1}\mathbf {a} _{1}+n_{2}\mathbf {a} _{2}+n_{3}\mathbf {a} _{3}

gdzie n _i są dowolnymi liczbami całkowitymi, a a _i są prymitywnymi wektorami translacji lub prymitywnymi wektorami, które leżą w różnych kierunkach (niekoniecznie wzajemnie prostopadłe) i obejmują sieć. Wybór prymitywnych wektorów dla danej sieci Bravaisa nie jest wyjątkowy. Podstawowym aspektem każdej sieci Bravais jest to, że dla każdego wyboru kierunku, sieć będzie wyglądać dokładnie tak samo z każdego z dyskretnych punktów sieci, patrząc w wybranym kierunku.

Koncepcja sieci Bravais służy do formalnego zdefiniowania układu krystalicznego i jego (skończonych) granic. Kryształu składa się z jednego lub więcej atomów, zwany podstawą lub motyw w każdym punkcie sieci krystalicznej. Podstawa może składać się z atomów , cząsteczek lub polimerów ciągów stałych i krata zawiera lokalizacje podłoża.

Dwie sieci Bravais są często uważane za równoważne, jeśli mają izomorficzne grupy symetrii. W tym sensie istnieje 5 możliwych siatek Bravaisa w przestrzeni dwuwymiarowej i 14 możliwych siatek Bravaisa w przestrzeni trójwymiarowej. 14 możliwych grup symetrii sieci Bravais to 14 z 230 grup przestrzennych . W kontekście klasyfikacji grup przestrzennych, kraty Bravaisa nazywane są również klasami Bravais, klasami arytmetycznymi Bravais lub stadami Bravais.

Komórka elementarna

W krystalografii istnieje pojęcie komórki elementarnej, która obejmuje przestrzeń między sąsiednimi punktami sieciowymi, a także dowolne atomy w tej przestrzeni. Komórka elementarna jest zdefiniowana jako przestrzeń, która po przesunięciu przez podzbiór wszystkich wektorów opisanych przez , wypełnia przestrzeń sieci bez nakładania się lub pustych przestrzeni. (Tzn. przestrzeń sieci jest wielokrotnością komórki elementarnej.) Istnieją głównie dwa typy komórek elementarnych: pierwotne komórki elementarne i konwencjonalne komórki elementarne. Pierwotna komórka jest najmniejszym składnikiem sieci (lub kryształu), który po ułożeniu razem z operacjami translacji sieci odtwarza całą sieć (lub kryształ). Zwróć uwagę, że tłumaczenia muszą być operacjami tłumaczenia kraty, które powodują, że krata po tłumaczeniu pojawia się niezmieniona. Gdyby zezwolono na dowolne tłumaczenia, można by na przykład zrobić prymitywną komórkę o połowę mniejszą od prawdziwej i tłumaczyć dwa razy częściej. Innym sposobem zdefiniowania rozmiaru komórki pierwotnej, który pozwala uniknąć wywoływania operacji translacji sieci, jest powiedzenie, że komórka pierwotna jest najmniejszym możliwym składnikiem sieci (lub kryształu), który można powtórzyć, aby odtworzyć całą sieć (lub kryształ). i zawiera dokładnie jeden punkt sieci. W obu definicjach prymitywna komórka charakteryzuje się małym rozmiarem. Istnieje oczywiście wiele możliwości wyboru komórki, która może odtworzyć całą sieć po ułożeniu w stos (na przykład dwie połówki sieci), a wymóg minimalnego rozmiaru odróżnia komórkę pierwotną od wszystkich innych prawidłowych, powtarzających się jednostek. Jeśli sieć lub kryształ są dwuwymiarowe, pierwotna komórka ma minimalną powierzchnię; podobnie w 3 wymiarach komórka prymitywna ma minimalną objętość. Pomimo tego sztywnego wymogu minimalnego rozmiaru, nie ma jednego unikalnego wyboru prymitywnej komórki elementarnej. W rzeczywistości wszystkie komórki, których granice są prymitywnymi wektorami translacji, będą prymitywnymi komórkami jednostkowymi. Fakt, że nie istnieje unikalny wybór prymitywnych wektorów translacji dla danej sieci, prowadzi do mnogości możliwych prymitywnych komórek elementarnych. Z drugiej strony, konwencjonalne komórki elementarne niekoniecznie są komórkami o minimalnym rozmiarze. Są one wybierane wyłącznie dla wygody i często są wykorzystywane do celów ilustracyjnych. Są luźno zdefiniowane. $\mathbf {R} =n_{1}\mathbf {a} _{1}+n_{2}\mathbf {a} _{2}+n_{3}\mathbf {a} _{3}$

Pierwotne komórki elementarne definiuje się jako komórki elementarne o najmniejszej objętości dla danego kryształu. (Kryształ jest siecią i bazą w każdym punkcie sieci.) Aby mieć najmniejszą objętość komórki, prymitywna komórka elementarna musi zawierać (1) tylko jeden punkt sieci i (2) minimalną ilość składników bazowych (np. minimalną liczba atomów w bazie). Dla pierwszego wymagania, liczenie liczby punktów sieci w komórce elementarnej jest takie, że jeśli punkt sieci jest współdzielony przez m sąsiednich komórek elementarnych wokół tego punktu sieci, to punkt jest liczony jako 1/ m . Ten ostatni wymóg jest konieczny, ponieważ istnieją kryształy, które można opisać więcej niż jedną kombinacją sieci i podstawy. Na przykład kryształ, oglądany przez siatkę z jednorodnymi atomami znajdującymi się w każdym punkcie sieci (najprostsza forma bazy), może być również widziany przez inną sieć z bazą dwóch atomów. W tym przypadku prymitywna komórka elementarna jest komórką elementarną mającą tylko jeden punkt sieci w pierwszym sposobie opisu kryształu w celu zapewnienia najmniejszej objętości komórki elementarnej.

Może istnieć więcej niż jeden sposób wybrania komórki pierwotnej dla danego kryształu, a każdy wybór będzie miał inny kształt komórki pierwotnej, ale objętość komórki pierwotnej jest taka sama dla każdego wyboru i każdy wybór będzie miał tę właściwość, że -jedna korespondencja może być ustalona między prymitywnymi komórkami elementarnymi a dyskretnymi punktami sieciowymi nad powiązaną siecią. Wszystkie prymitywne komórki elementarne o różnych kształtach dla danego kryształu mają z definicji tę samą objętość; Dla danego kryształu, jeśli n jest gęstością punktów sieci w sieci zapewniającej minimalną ilość składników bazowych, a v jest objętością wybranej komórki pierwotnej, to nv = 1 daje v = 1/ n , a więc każda komórka pierwotna ma taką samą objętość 1/ n .

Spośród wszystkich możliwych komórek prymitywnych dla danego kryształu, oczywistą komórką prymitywną może być równoległościan utworzony przez wybrany zestaw prymitywnych wektorów translacji. (Ponownie, wektory te muszą tworzyć sieć z minimalną ilością składników bazowych.) To jest zbiór wszystkich punktów, gdzie i jest wybranym wektorem pierwotnym. Ta prymitywna komórka nie zawsze wykazuje wyraźną symetrię danego kryształu. W takim przypadku często stosuje się konwencjonalną komórkę elementarną, która łatwo wyświetla symetrię kryształu. Konwencjonalna objętość komórki elementarnej będzie całkowitą wielokrotnością pierwotnej objętości komórki elementarnej. $\mathbf {r} =x_{1}\mathbf {a} _{1}+x_{2}\mathbf {a} _{2}+x_{3}\mathbf {a} _{3}$ $0\leq x_{i}<1$ ${\ Displaystyle \ mathbf {a} _ {i}}$

Pochodzenie koncepcji

W dwóch wymiarach dowolna sieć może być określona przez długość jej dwóch prymitywnych wektorów translacji i kąt między nimi. Istnieje nieskończona liczba możliwych siatek, które można w ten sposób opisać. Pożądany jest jakiś sposób kategoryzowania różnych typów sieci. Jednym ze sposobów, aby to zrobić, jest rozpoznanie, że niektóre sieci mają wrodzoną symetrię. Można nałożyć warunki na długość prymitywnych wektorów translacji i kąt między nimi, aby uzyskać różne sieci symetryczne. Same symetrie są podzielone na różne typy, takie jak symetrie lustrzane, symetrie inwersyjne, symetrie obrotowe i symetrie translacyjne. Szczególna kombinacja tych symetrii (na przykład dwukrotna symetria obrotowa i symetria lustrzana) nazywana jest grupą punktową . W ten sposób kraty można kategoryzować na podstawie tego, jaka grupa punktowa ma do nich zastosowanie. Najbardziej podstawowa grupa punktowa odpowiada niezmienności obrotowej przy 2π i π, czyli 1- i 2-krotnej symetrii obrotowej. W rzeczywistości dotyczy to automatycznie wszystkich dwuwymiarowych sieci i jest najbardziej ogólną grupą punktową. Kraty zawarte w tej grupie (technicznie wszystkie kraty, ale umownie wszystkie kraty, które nie należą do żadnej z pozostałych grup punktowych) nazywane są kratami ukośnymi . Stamtąd, w dwóch wymiarach, są 4 kolejne grupy punktów (lub równoważnie 4 rodzaje ograniczeń długości/kątów prymitywnych wektorów translacji), które odpowiadają 4 pozostałym kategoriom sieci: kwadratowej, sześciokątnej, prostokątnej i wyśrodkowanej . Tak więc w sumie jest 5 krat Bravais w 2 wymiarach. Podobnie w 3 wymiarach jest 14 krat Bravais: 1 ogólna kategoria „koszyka na śmieci” ( trójkliniczna ) i 13 innych kategorii. Te 14 typów sieci jest dalej pogrupowanych dla wygody w 7 systemów sieci (trójskośny, jednoskośny, rombowy, tetragonalny, sześcienny, trygonalny i sześciokątny).

W 2 wymiarach

W przestrzeni dwuwymiarowej znajduje się 5 siatek Bravaisa, pogrupowanych w cztery rodziny kryształów .

Uwaga: Na diagramach komórek elementarnych w poniższej tabeli punkty sieci są przedstawione za pomocą czarnych kółek, a komórki elementarne są przedstawione za pomocą równoległoboków (które mogą być kwadratami lub prostokątami) obrysowanymi na czarno. Chociaż każdy z czterech rogów każdego równoległoboku łączy się z punktem sieciowym, tylko jeden z czterech punktów sieci technicznie należy do danej komórki elementarnej, a każdy z pozostałych trzech punktów sieci należy do jednej z sąsiednich komórek elementarnych. Można to zaobserwować, wyobrażając sobie przesunięcie równoległoboku komórki elementarnej nieco w lewo i nieco w dół, pozostawiając wszystkie czarne okręgi punktów sieci nieruchome.

Rodzina kryształów	Grupa punktowa ( notacja Schönfliesa )	5 krat Bravais
Rodzina kryształów	Grupa punktowa ( notacja Schönfliesa )	prymitywny (p)	Wyśrodkowany (c)
Jednoskośna (m)	C ₂	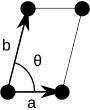Skośny (mp)
rombowy (o)	D ₂	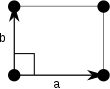Prostokątny (op)	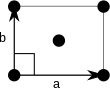Wyśrodkowany prostokątny (oc)
Czworokąt (t)	D ₄	Kwadrat (tp)
Sześciokątny (h)	D ₆	Sześciokątny (KM)

Komórki elementarne są określone w zależności od stosunku długości krawędzi komórek ( i b ), a kąt między nimi ( θ ). Pole powierzchni komórki elementarnej można obliczyć obliczając normę || a × b || , gdzie a i b są wektorami sieciowymi. Poniżej podano właściwości rodzin kryształów:

Rodzina kryształów	Powierzchnia	Odległości osiowe (długości krawędzi)	Kąt osiowy
Jednoskośny	$ab\,\sin \theta$	≠ b	θ ≠ 90°
rombowy	$ab$	≠ b	θ = 90°
Tetragonalny	${\ Displaystyle a ^ {2}}$	a = b	θ = 90°
Sześciokątny	${\frac {\sqrt {3}} {2}} \ a ^ {2}$	a = b	θ = 120°

W 3 wymiarach

2×2×2 komórki elementarne diamentowej sieci sześciennej

W przestrzeni trójwymiarowej znajduje się 14 krat Bravais. Uzyskuje się je poprzez połączenie jednego z siedmiu systemów kratowych z jednym z typów centrowania. Typy centrowania identyfikują lokalizacje punktów sieci w komórce elementarnej w następujący sposób:

Prymitywne (P): punkty sieci tylko na rogach komórki (czasami nazywane prostymi)
Wyśrodkowany względem podstawy (A, B lub C): punkty kratowe na rogach komórki z jednym dodatkowym punktem w środku każdej powierzchni jednej pary równoległych ścian komórki (czasami nazywane wyśrodkowanymi na końcu)
Wyśrodkowany na ciele (I): punkty kratowe na rogach komórki, z jednym dodatkowym punktem w środku komórki
Face-centered (F): punkty kratowe na rogach komórki, z jednym dodatkowym punktem w środku każdej z powierzchni komórki

Nie wszystkie kombinacje systemów kratowych i typów centrowania są potrzebne do opisania wszystkich możliwych krat, ponieważ można wykazać, że kilka z nich jest w rzeczywistości równoważnych sobie. Na przykład, sieć jednoskośną I można opisać siecią jednoskośną C przez inny wybór osi kryształu. Podobnie, wszystkie sieci centrowane A lub B mogą być opisane przez centrowanie C lub P. Zmniejsza to liczbę kombinacji do 14 konwencjonalnych kratek Bravais, pokazanych w poniższej tabeli. Pod każdym diagramem znajduje się symbol Pearsona dla tej sieci Bravais.

Uwaga: Na diagramach komórek elementarnych w poniższej tabeli pokazane są wszystkie punkty sieci na granicy komórki (rogi i powierzchnie); jednak nie wszystkie z tych punktów sieci należą technicznie do danej komórki elementarnej. Można to zobaczyć, wyobrażając sobie lekkie przesunięcie komórki elementarnej w kierunku ujemnym każdej osi, utrzymując stałe punkty sieci. Z grubsza można to traktować jako przesunięcie komórki elementarnej nieco w lewo, nieco w dół i nieco poza ekran. To pokazuje, że tylko jeden z ośmiu narożnych punktów kratownicy (w szczególności przedni, lewy, dolny) należy do danej komórki elementarnej (pozostałe siedem punktów siatki należy do sąsiednich komórek elementarnych). Ponadto tylko jeden z dwóch punktów siatki pokazanych na górnej i dolnej powierzchni w kolumnie wyśrodkowanej na podstawie należy do danej komórki elementarnej . Wreszcie, tylko trzy z sześciu punktów sieci na ścianach w kolumnie Face-centered należą do danej komórki elementarnej .

Rodzina kryształów	System kratowy	Grupa punktowa ( notacja Schönfliesa )	14 krat Bravais
Rodzina kryształów	System kratowy	Grupa punktowa ( notacja Schönfliesa )	prymitywny (P)	Wyśrodkowany na podstawie (S)	Skoncentrowany na ciele (I)	Wyśrodkowany na twarzy (F)
Trójklinika (a)		C _i	aP
Jednoskośna (m)		C _2h	poseł	SM
rombowy (o)		D _2h	oP	oS	mój	z
Czworokąt (t)		D _4h	tP		tI
Sześciokątny (h)	Rhomboedral	D _3d	hR
Sześciokątny (h)	Sześciokątny	D _6h	HP
Sześcienny (c)		O _H	cP		cI	cF

Komórki elementarne są określane zgodnie z sześcioma parametrami sieci, którymi są względne długości krawędzi komórek ( a , b , c ) oraz kąty między nimi ( α , β , γ ). Objętość komórki elementarnej może być obliczona przez ocenę produktu potrójne · ( b x c ) , w którym a , b i c są wektory kraty. Poniżej podano właściwości systemów kratowych:

Rodzina kryształów	System kratowy	Tom	Odległości osiowe (długości krawędzi)	Kąty osiowe	Odpowiednie przykłady
Trójklinika		${\ Displaystyle abc {\ sqrt {1-\ cos ^ {2} \ alfa - \ cos ^ {2} \ beta - \ cos ^ {2} \ gamma +2 \ cos \ alfa \ cos \ beta \ cos \ gamma }}}$	(Wszystkie pozostałe przypadki)		K ₂ Cr ₂ O ₇ , CuSO ₄ · 5 H ₂ O , H ₃ BO ₃
Jednoskośny		$abc\,\sin \beta$	≠ C	α = γ = 90°, β ≠ 90°	Siarka jednoskośna , Na ₂ SO ₄ ·10H ₂ O , PbCrO ₃
rombowy		$abc$	a ≠ b ≠ c	α = β = γ = 90°	Siarka rombowa , KNO ₃ , BaSO ₄
Tetragonalny		$a^{2}c$	a = b ≠ c	α = β = γ = 90°	Biała cyna , SnO ₂ , TiO ₂ , CaSO ₄
Sześciokątny	Rhomboedral	${\ Displaystyle a ^ {3} {\ sqrt {1-3 \ cos ^ {2} \ alfa +2 \ cos ^ {3} \ alfa }}}$	a = b = c	α = β = γ ≠ 90°	Kalcyt (CaCO ₃ ), cynober (HgS)
Sześciokątny	Sześciokątny	${\frac {\sqrt {3}}{2}}\,a^{2}c$	a = b	α = β = 90°, γ = 120°	grafit , ZnO , CdS
Sześcienny		${\ Displaystyle a ^ {3}}$	a = b = c	α = β = γ = 90°	NaCl , mieszanka cynku , miedź metaliczna , KCl , diament , srebro

W 4 wymiarach

W czterech wymiarach znajdują się 64 kraty Bravais. Spośród nich 23 jest prymitywnych, a 41 jest wyśrodkowanych. Dziesięć siatek Bravaisa podzieliło się na pary enancjomorficzne .

Zobacz też

Bibliografia

Dalsza lektura

Bravais, A. (1850). „Mémoire sur les systèmes formés par les points distribués régulièrement sur un plan ou dans l'espace” [Pamiętnik na temat systemów utworzonych przez punkty regularnie rozmieszczone na płaszczyźnie lub w przestrzeni]. J. Ecole Polytech . 19 : 1-128. (Angielski: Memoir 1, Crystallographic Society of America, 1949.)
Hahn, Theo, wyd. (2002). Międzynarodowe Tabele Krystalografii, Tom A: Symetria Grup Przestrzennych . Międzynarodowe Tabele Krystalografii. A (wyd. 5). Berlin, Nowy Jork: Springer-Verlag . doi : 10.1107/97809553602060000100 . Numer ISBN 978-0-7923-6590-7.

Zewnętrzne linki

Katalog krat (autorstwa Nebe i Sloane)
Smith, Walter Fox (2002). „Pieśń Bravais Kraty” .

Languages

In other projects