Współrzędne krzywoliniowe - Curvilinear coordinates

Współrzędne krzywoliniowe (u góry), afiniczne (po prawej) i kartezjańskie (po lewej) w przestrzeni dwuwymiarowej

W geometrii , krzywoliniowe współrzędne są Układ współrzędnych dla przestrzeni euklidesowej , w którym linie współrzędnych może być zakrzywiona. Te współrzędne mogą pochodzić z zestawu współrzędnych kartezjańskich przy użyciu przekształcenia, które jest lokalnie odwracalne (mapa jeden do jednego) w każdym punkcie. Oznacza to, że można przekonwertować punkt podany w kartezjańskim układzie współrzędnych na jego współrzędne krzywoliniowe iz powrotem. Nazwa współrzędne krzywoliniowe , wymyślona przez francuskiego matematyka Lamé , wywodzi się z faktu, że powierzchnie współrzędnych układów krzywoliniowych są zakrzywione.

Dobrze znanymi przykładami krzywoliniowych układów współrzędnych w trójwymiarowej przestrzeni euklidesowej ( R ³ ) są współrzędne cylindryczne i sferyczne . Powierzchnia współrzędnych kartezjańskich w tej przestrzeni jest płaszczyzną współrzędnych ; na przykład z = 0 definiuje płaszczyznę x - y . W tej samej przestrzeni powierzchnia współrzędnych r = 1 we współrzędnych sferycznych jest powierzchnią jednostki sfery , która jest zakrzywiona. Formalizm współrzędnych krzywoliniowych zapewnia ujednolicony i ogólny opis standardowych układów współrzędnych.

Współrzędne krzywoliniowe są często używane do określenia położenia lub rozkładu wielkości fizycznych, którymi mogą być na przykład skalary , wektory lub tensory . Wyrażenia matematyczne obejmujące te wielkości w rachunku wektorowym i analizie tensorowej (takie jak gradient , dywergencja , zwijanie i Laplacian ) można przekształcać z jednego układu współrzędnych do drugiego, zgodnie z regułami transformacji dla skalarów, wektorów i tensorów. Takie wyrażenia stają się wtedy poprawne dla dowolnego krzywoliniowego układu współrzędnych.

W niektórych zastosowaniach krzywoliniowy układ współrzędnych może być prostszy w użyciu niż układ kartezjański. Ruch cząstek pod wpływem sił centralnych jest zwykle łatwiejszy do rozwiązania we współrzędnych sferycznych niż we współrzędnych kartezjańskich; dotyczy to wielu fizycznych problemów z symetrią sferyczną zdefiniowaną w R ³ . Równania z warunkami brzegowymi, które następują po powierzchniach współrzędnych dla określonego krzywoliniowego układu współrzędnych, mogą być łatwiejsze do rozwiązania w tym układzie. Podczas gdy można opisać ruch cząstki w prostokątnym pudełku za pomocą współrzędnych kartezjańskich, ruch w sferze jest łatwiejszy w przypadku współrzędnych sferycznych. Współrzędne sferyczne są najpowszechniejszymi układami współrzędnych krzywoliniowych i są używane w naukach o Ziemi , kartografii , mechanice kwantowej , teoriach względności i inżynierii .

Ortogonalne współrzędne krzywoliniowe w 3 wymiarach

Współrzędne, baza i wektory

Rys. 1 - Powierzchnie współrzędnych, linie współrzędnych i osie współrzędnych ogólnych współrzędnych krzywoliniowych.

Rys. 2 - Powierzchnie współrzędnych, linie współrzędnych i osie współrzędnych sferycznych. Powierzchnie: r - kule, θ - stożki, φ - półpłaszczyzny; Linie: r - belki proste, θ - półkola pionowe, φ - koła poziome; Osie: r - belki proste, θ - styczne do półokręgów pionowych, φ - styczne do okręgów poziomych

Na razie rozważ przestrzeń 3D . Punkt P w przestrzeni 3d (lub jego wektor położenia r ) można zdefiniować za pomocą współrzędnych kartezjańskich ( x , y , z ) [odpowiednio zapisane ( x ¹ , x ² , x ³ )], przez , gdzie e _x , e _y , e _oo są standardową podstawę wektorów . ${\ Displaystyle \ mathbf {r} = x \ mathbf {e} _ {x} + r \ mathbf {e} _ {y} + z \ mathbf {e} _ {z}}$

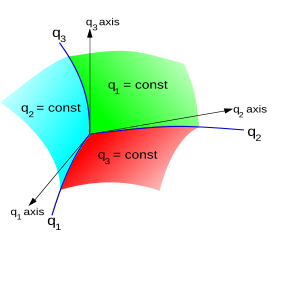
Może być również zdefiniowany przez jego współrzędne krzywoliniowe ( q ¹ , q ² , q ³ ), jeśli ta trójka liczb definiuje pojedynczy punkt w sposób jednoznaczny. Zależność między współrzędnymi jest wtedy podana przez funkcje transformacji odwracalnej:

${\ Displaystyle x = f ^ {1} (q ^ {1}, q ^ {2}, q ^ {3}), \ y = f ^ {2} (q ^ {1}, q ^ {2} },q^{3}),\,z=f^{3}(q^{1},q^{2},q^{3})}$

${\displaystyle q^{1}=g^{1}(x,y,z),\q^{2}=g^{2}(x,y,z),\,q^{3} =g^{3}(x,y,z)}$

Powierzchnie q ¹ = stała, q ² = stała, q ³ = stała są nazywane powierzchniami współrzędnych ; a krzywe przestrzenne utworzone przez ich przecięcie parami nazywane są krzywymi współrzędnych . Na osi współrzędnych są określone przez styczne do krzywej przecięcia współrzędnych na trzech powierzchniach. Nie są one ogólnie stałymi kierunkami w przestrzeni, co zdarza się w przypadku prostych współrzędnych kartezjańskich, a zatem ogólnie nie ma naturalnej globalnej podstawy dla współrzędnych krzywoliniowych.

W układzie kartezjańskim standardowe wektory bazowe można wyprowadzić z pochodnej położenia punktu P względem lokalnej współrzędnej

${\ Displaystyle \ mathbf {e} _ {x} = {\ dfrac {\ częściowy \ mathbf {r}} {\ częściowy x}}; \; \ mathbf {e} _ {y} = {\ dfrac {\ częściowy \mathbf {r} }{\częściowy r}};\;\mathbf {e} _{z}={\dfrac {\częściowy \mathbf {r} }{\częściowy z}}.}$

Zastosowanie tych samych pochodnych do układu krzywoliniowego lokalnie w punkcie P definiuje naturalne wektory bazowe:

${\ Displaystyle \ mathbf {h} _ {1} = {\ dfrac {\ częściowy \ mathbf {r}} {\ częściowy q ^ {1}}}; \; \ mathbf {h} _ {2} = {\ dfrac {\częściowy \mathbf {r} }{\częściowy q^{2}}};\;\mathbf {h} _{3}={\dfrac {\częściowy \mathbf {r} }{\częściowy q^ {3}}}.}$

Taką bazę, której wektory zmieniają kierunek i/lub wielkość z punktu do punktu nazywamy bazą lokalną . Wszystkie podstawy związane ze współrzędnymi krzywoliniowymi są z konieczności lokalne. Wektory bazowe , które są takie same we wszystkich punktach, są bazami globalnymi i mogą być powiązane tylko z liniowymi lub afinicznymi układami współrzędnych .

W tym artykule e jest zarezerwowane dla bazy standardowej (kartezjańskiej), a h lub b dla bazy krzywoliniowej.

Mogą one nie mieć długości jednostkowej, a także mogą nie być ortogonalne. W przypadku, gdy są one ortogonalne we wszystkich punktach, w których pochodne są dobrze zdefiniowane, definiujemy współczynniki Lamé(za Gabrielem Lamé ) autorstwa

${\displaystyle h_{1}=|\mathbf {h}_{1}|;\;h_{2}=|\mathbf {h}_{2}|;\;h_{3}=|\mathbf { h} _{3}|}$

a krzywoliniowe wektory bazy ortonormalnej przez

${\ Displaystyle \ mathbf {b} _ {1} = {\ dfrac {\ mathbf {h} _ {1}} {h_ {1}}}; \; \ mathbf {b} _ {2} = {\ dfrac {\mathbf {h} _{2}}{h_{2}}};\;\mathbf {b} _{3}={\dfrac {\mathbf {h} _{3}}{h_{3} }}.}$

Te wektory bazowe mogą zależeć od pozycji P ; dlatego konieczne jest, aby nie zakładać, że są stałe w regionie. (Z technicznego punktu widzenia tworzą one podstawę dla wiązki stycznej z w P , a więc są lokalne dla P .) ${\ Displaystyle \ mathbb {R} ^ {3}}$

Ogólnie rzecz biorąc, współrzędne krzywoliniowe pozwalają, aby wektory bazy naturalnej h _i nie wszystkie były wzajemnie prostopadłe do siebie i nie muszą mieć jednostki długości: mogą mieć dowolną wielkość i kierunek. Zastosowanie bazy ortogonalnej sprawia, że ​​manipulacje wektorami są prostsze niż w przypadku nieortogonalnych. Jednak niektóre dziedziny fizyki i inżynierii , w szczególności mechanika płynów i mechanika ośrodków ciągłych , wymagają nieortogonalnych podstaw do opisu deformacji i transportu płynów, aby uwzględnić skomplikowane zależności kierunkowe wielkości fizycznych. Omówienie ogólnej sprawy pojawi się później na tej stronie.

Rachunek wektorowy

Elementy różnicowe

W ortogonalnych współrzędnych krzywoliniowych, ponieważ całkowita zmiana różniczkowa w r wynosi

${\ Displaystyle d \ mathbf {r} = {\ dfrac {\ częściowy \ mathbf {r}} {\ częściowy q ^ {1}}} dq ^ {1} + {\ dfrac {\ częściowy \ mathbf {r}} {\częściowe q^{2}}}dq^{2}+{\dfrac {\częściowe \mathbf {r} }{\częściowe q^{3}}}dq^{3}=h_{1}dq^ {1}\mathbf {b} _{1}+h_{2}dq^{2}\mathbf {b} _{2}+h_{3}dq^{3}\mathbf {b} _{3} }$

więc współczynniki skali są ${\ Displaystyle h_ {i} = \ lewo | {\ Frac {\ częściowy \ mathbf {r}} {\ częściowy q ^ {i}}} \ prawej |}$

We współrzędnych nieortogonalnych długość jest dodatnim pierwiastkiem kwadratowym z (z konwencją sumowania Einsteina ). Sześć niezależnych iloczynów skalarnych g _ij = h _i . H _J naturalnych wektorów bazowych uogólnić trzy współczynniki skali zdefiniowano powyżej dla współrzędnych prostokątnych. Dziewięć g _ij to składowe tensora metrycznego , który ma tylko trzy niezerowe składowe we współrzędnych ortogonalnych: g ₁₁ = h ₁ h ₁ , g ₂₂ = h ₂ h ₂ , g ₃₃ = h ₃ h ₃ . ${\ Displaystyle d \ mathbf {r} = dq ^ {1} \ mathbf {h} _ {1} + dq ^ {2} \ mathbf {h} _ {2} + dq ^ {3} \ mathbf {h} _{3}}$${\ Displaystyle d \ mathbf {r} \ cdot d \ mathbf {r} = dq ^ {i} dq ^ {j} \ mathbf {h} _ {i} \ cdot \ mathbf {h} _ {j}}$

Bazy kowariantne i kontrawariantne

Wektor v ( czerwony ) reprezentowany przez • bazę wektora ( żółty , lewy : e ₁ , e ₂ , e ₃ ), wektory styczne do współrzędnych krzywych ( czarny ) oraz • bazę kowektorową lub cobasis ( niebieski , prawy: e ¹ , e ² , e ³ , wektory normalne do koordynowania powierzchni ( szary ) w ogólnych (niekoniecznie ortogonalnych ) współrzędnych krzywoliniowych ( q ¹ , q ² , q ³ ). Podstawa i kobaza nie pokrywają się, chyba że układ współrzędnych jest ortogonalny.

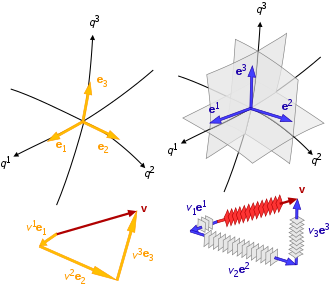
Gradienty przestrzenne, odległości, pochodne czasowe i współczynniki skali są powiązane w układzie współrzędnych dwiema grupami wektorów bazowych:

W konsekwencji ogólny krzywoliniowy układ współrzędnych ma dwa zestawy wektorów bazowych dla każdego punktu: { b ₁ , b ₂ , b ₃ } jest bazą kowariantną, a { b ¹ , b ² , b ³ } jest kontrawariantną (inaczej odwrotnością) podstawa. Kowariantne i kontrawariantne typy wektorów bazowych mają identyczny kierunek dla ortogonalnych krzywoliniowych układów współrzędnych, ale jak zwykle mają odwrócone jednostki względem siebie.

Zwróć uwagę na następującą ważną równość:

${\ Displaystyle \ mathbf {b} ^ {i} \ cdot \ mathbf {b} _ {j} = \ delta _ {j} ^ {i}}$

gdzie oznacza uogólnioną deltę Kroneckera . ${\ Displaystyle \ delta _ {j} ^ {i}}$

Dowód

W kartezjańskim układzie współrzędnych możemy zapisać iloczyn skalarny jako: ${\ Displaystyle (\ mathbf {e} _ {x}, \ mathbf {e} _ {y}, \ mathbf {e} _ {z})}$ ${\ Displaystyle \ mathbf {b} _ {i} \ cdot \ mathbf {b} ^ {j} = ({\ dfrac {\ częściowy x} {\ częściowy q_ {i}}}, {\ dfrac {\ częściowy y }{\częściowe q_{i}}},{\dfrac {\częściowe z}{\częściowe q_{i}}})\cdot ({\dfrac {\częściowe q_{j}}{\częściowe x}}, {\dfrac {\częściowy q_{j}}{\częściowy y}},{\dfrac {\częściowy q_{j}}{\częściowy z}})={\dfrac {\częściowy x}{\częściowy q_{ i}}}{\dfrac {\częściowe q_{j}}{\częściowe x}}+{\dfrac {\częściowe y}{\częściowe q_{i}}}{\dfrac {\częściowe q_{j}} {\częściowy y}}+{\dfrac {\częściowy z}{\częściowy q_{i}}}{\dfrac {\częściowy q_{j}}{\częściowy z}}}$ Rozważ nieskończenie małe przemieszczenie . Niech dq 1 , dq 2 i dq 3 oznaczają odpowiednio nieskończenie małe zmiany współrzędnych krzywoliniowych q 1 , q 2 i q 3 . ${\ Displaystyle d \ mathbf {r} = dx \ cdot \ mathbf {e} _ {x} + dy \ cdot \ mathbf {e} _ {y} + dz \ cdot \ mathbf {e} _ {z}}$ Zgodnie z regułą łańcucha dq 1 można wyrazić jako: ${\ Displaystyle dq_ {1} = {\ dfrac {\ częściowy q_ {1}}{\ częściowy x}} dx + {\ dfrac {\ częściowy q_ {1}} {\ częściowy y}} dy + {\ dfrac {\ częściowy q_{1}}{\częściowy z}}dz={\dfrac {\częściowy q_{1}}{\częściowy x}}dx+{\dfrac {\częściowy q_{1}}{\częściowy y}}({ \dfrac {\częściowy y}{\częściowy q_{1}}}dq_{1}+{\dfrac {\częściowy y}{\częściowy q_{2}}}dq_{2}+{\dfrac {\częściowy y }{\częściowe q_{3}}}dq_{3})+{\dfrac {\częściowe q_{1}}{\częściowe z}}({\dfrac {\częściowe z}{\częściowe q_{1}} }dq_{1}+{\dfrac {\partial z}{\partial q_{2}}}dq_{2}+{\dfrac {\partial z}{\partial q_{3}}}dq_{3}) }$ Jeżeli przemieszczenie dr jest takie, że dq 2 = dq 3 = 0, tj. wektor położenia r przesuwa się o nieskończenie małą wartość wzdłuż osi współrzędnych q 2 = const i q 3 = const, to: ${\displaystyle dq_{1}={\dfrac {\częściowy q_{1}}{\częściowy x}}dx+{\dfrac {\częściowy q_{1}}{\częściowy y}}{\dfrac {\częściowy y }{\partial q_{1}}}dq_{1}+{\dfrac {\partial q_{1}}{\partial z}}{\dfrac {\partial z}{\partial q_{1}}}dq_ {1}}$ Dzieląc przez dq 1 i biorąc granicę dq 1 → 0: ${\ Displaystyle 1 = {\ dfrac {\ częściowy q_ {1}}{\ częściowy x}} {\ dfrac {\ częściowy x} {\ częściowy q_ {1}}} + {\ dfrac {\ częściowy q_ {1} }{\częściowy r}}{\dfrac {\częściowy r}{\częściowy r_{1}}}+{\dfrac {\częściowy r_{1}}{\częściowy z}}{\dfrac {\częściowy z} {\partial q_{1}}}={\dfrac {\częściowy x}{\częściowy q_{1}}}{\dfrac {\częściowy q_{1}}{\częściowy x}}+{\dfrac {\ częściowe r}{\częściowe q_{1}}}{\dfrac {\częściowe q_{1}}{\częściowe q_}}+{\dfrac {\częściowe z}{\częściowe q_{1}}}{\dfrac {\częściowe q_{1}}{\częściowe z}}}$ lub równoważnie: ${\ Displaystyle \ mathbf {b} _ {1} \ cdot \ mathbf {b} ^ {1} = 1}$ Teraz, jeśli przemieszczenie dr jest takie, że dq 1 =dq 3 =0, tj. wektor położenia r przesuwa się o nieskończenie małą wartość wzdłuż osi współrzędnych q 1 =const i q 3 =const, wtedy: ${\ Displaystyle 0 = {\ dfrac {\ częściowy q_ {1}}{\ częściowy x}} dx + {\ dfrac {\ częściowy q_ {1}}{\ częściowy y}}{\ dfrac {\ częściowy y}{\ częściowe q_{2}}}dq_{2}+{\dfrac {\częściowe q_{1}}{\partial z}}{\dfrac {\partial z}{\częściowe q_{2}}}dq_{2} }$ Dzieląc przez dq 2 i biorąc granicę dq 2 → 0: ${\ Displaystyle 0 = {\ dfrac {\ częściowy q_ {1}}{\ częściowy x}} {\ dfrac {\ częściowy x} {\ częściowy q_ {2}}} + {\ dfrac {\ częściowy q_ {1} }{\częściowy r}}{\dfrac {\częściowy r}{\częściowy r_{2}}}+{\dfrac {\częściowy r_{1}}{\częściowy z}}{\dfrac {\częściowy z} {\częściowy q_{2}}}={\dfrac {\częściowy x}{\częściowy q_{2}}}{\dfrac {\częściowy q_{1}}{\częściowy x}}+{\dfrac {\ częściowy rok}{\częściowy kwartał_{2}}}{\dfrac {\częściowy kwartał_{1}}{\częściowy rok}}+{\dfrac {\częściowy z}{\częściowy kwartał_{2}}}{\dfrac {\częściowe q_{1}}{\częściowe z}}}$ lub równoważnie: ${\ Displaystyle \ mathbf {b} _ {2} \ cdot \ mathbf {b} ^ {1} = 0}$ I tak dalej w przypadku innych produktów kropkowych. Dowód alternatywny: ${\ Displaystyle \ delta _ {j} ^ {i} dq ^ {j} = dq ^ {i} = \ nabla q ^ {i} \ cdot d \ mathbf {r} = \ mathbf {b} ^ {i} \cdot {\dfrac {\częściowy \mathbf {r} }{\częściowy q^{j}}}dq^{j}=\mathbf {b} ^{i}\cdot \mathbf {b} _{j} dq^{j}}$ i zakłada się konwencję sumowania Einsteina .

Wektor v może być określony jako podstawa, tj.

${\ Displaystyle \ mathbf {v} = v ^ {1} \ mathbf {b} _ {1} + v ^ {2} \ mathbf {b} _ {2} + v ^ {3} \ mathbf {b} _ {3}=v_{1}\mathbf {b} ^{1}+v_{2}\mathbf {b} ^{2}+v_{3}\mathbf {b} ^{3}}$

Korzystając z konwencji sumowania Einsteina, wektory bazowe odnoszą się do składowych przez

${\ Displaystyle \ mathbf {v} \ cdot \ mathbf {b} ^ {i} = v ^ {k} \ mathbf {b} _ {k} \ cdot \ mathbf {b} ^ {i} = v ^ {k }\delta _{k}^{i}=v^{i}}$

${\ Displaystyle \ mathbf {v} \ cdot \ mathbf {b} _ {i} = v_ {k} \ mathbf {b} ^ {k} \ cdot \ mathbf {b} _ {i} = v_ {k} \ delta _{i}^{k}=v_{i}}$

i

${\ Displaystyle \ mathbf {v} \ cdot \ mathbf {b} _ {i} = v ^ {k} \ mathbf {b} _ {k} \ cdot \ mathbf {b} _ {i} = g_ {ki} v^{k}}$

${\ Displaystyle \ mathbf {v} \ cdot \ mathbf {b} ^ {i} = v_ {k} \ mathbf {b} ^ {k} \ cdot \ mathbf {b} ^ {i} = g ^ {ki} v_{k}}$

gdzie g jest tensorem metrycznym (patrz poniżej).

Wektor można określić za pomocą współrzędnych kowariantnych (wskaźniki obniżone, zapisane v _k ) lub współrzędne kontrawariantne (wskaźniki podwyższone, zapisane v ^k ). Z powyższych sum wektorowych widać, że współrzędne kontrawariantne są związane z kowariantnymi wektorami bazowymi, a kowariantne współrzędne są związane z kontrawariantnymi wektorami bazowymi.

Kluczową cechą reprezentacji wektorów i tensorów w kategoriach składowych indeksowanych i wektorów bazowych jest niezmienność w tym sensie, że składowe wektorów transformujące się w sposób kowariantny (lub kontrawariantny) są sparowane z wektorami bazowymi transformującymi się w sposób kontrawariantny (lub kontrawariantny). sposób kowariantny).

Integracja

Konstruowanie bazy kowariantnej w jednym wymiarze

Rys. 3 – Transformacja lokalnej bazy kowariantnej w przypadku ogólnych współrzędnych krzywoliniowych

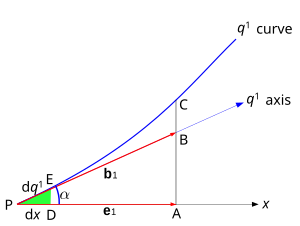
Rozważmy krzywą jednowymiarową pokazaną na Rys. 3. W punkcie P , przyjętym jako początek , x jest jedną ze współrzędnych kartezjańskich, a q ¹ jest jedną ze współrzędnych krzywoliniowych. Lokalny (niejednostkowy) wektor bazowy to b ₁ (oznaczony jako h ₁ powyżej, z b zarezerwowanym dla wektorów jednostkowych) i jest zbudowany na osi q ^{1 ,} która jest styczną do tej linii współrzędnych w punkcie P . Oś q ¹ i tym samym wektor b ₁ tworzą kąt z kartezjańską osią x i kartezjańskim wektorem bazowym e ₁ . ${\ Displaystyle \ alfa}$

Z trójkąta PAB widać, że

${\ Displaystyle \ cos \ alfa = {\ cfrac {| \ mathbf {e} _ {1} |} {| \ mathbf {b} _ {1} |}} \ quad \ prawostrzałka \ quad | \ mathbf {e} _{1}|=|\mathbf {b} _{1}|\cos \alpha }$

gdzie | e ₁ |, | b ₁ | są wielkościami dwóch wektorów bazowych, tj. przecięcia skalarne PB i PA . PA jest również rzutem b ₁ na oś x .

Jednak ta metoda transformacji wektorów bazowych przy użyciu kierunkowych cosinusów nie ma zastosowania do współrzędnych krzywoliniowych z następujących powodów:

1. Zwiększając odległość od P , kąt między linią krzywą q ¹ a osią kartezjańską x coraz bardziej odbiega od .${\ Displaystyle \ alfa}$
2. W odległości PB prawdziwy kąt to ten, który tworzy styczna w punkcie C z osią x, a ten ostatni kąt jest wyraźnie różny od .${\ Displaystyle \ alfa}$

Kąty, że Q ¹ line, które tworzą z osią X osi, zbliżyć się do wartości im bliżej przemieszcza się w kierunku punktu P i stają się dokładnie równe w P .

Niech punkt E będzie położony bardzo blisko P , tak blisko, aby odległość PE była nieskończenie mała. Następnie PE zmierzona na Q ¹ osi prawie zbieżny z PE , mierzone Q ¹ linii. Jednocześnie stosunek PD/PE ( PD jest rzutem PE na oś x ) staje się prawie dokładnie równy . ${\ Displaystyle \ cos \ alfa}$

Nieskończenie małe punkty przecięcia PD i PE oznaczymy odpowiednio jako dx i d q ¹ . Następnie

${\ Displaystyle \ cos \ alfa = {\ cfrac {dx} {dq ^ {1}}} = {\ Frac {| \ mathbf {e} _ {1} |} {| \ mathbf {b} _ {1} |}}}$.

Zatem kierunkowe cosinusy mogą być podstawiane w transformacjach z dokładniejszymi stosunkami między nieskończenie małymi punktami przecięcia współrzędnych. Wynika z tego, że składowa (rzut) b ₁ na osi x to

${\ Displaystyle p ^ {1} = \ mathbf {b} _ {1} \ cdot {\ cfrac {\ mathbf {e} _ {1}} {| \ mathbf {e} _ {1} |}} = | \mathbf {b} _{1}|{\cfrac {|\mathbf {e} _{1}|}{|\mathbf {e} _{1}|}}\cos \alpha =|\mathbf {b } _{1}|{\cfrac {dx}{dq^{1}}}\quad \Rightarrow \quad {\cfrac {p^{1}}{|\mathbf {b} _{1}|}} ={\cfrac {dx}{dq^{1}}}}$.

Jeśli q ⁱ = q ⁱ ( x ₁ , x ₂ , x ₃ ) oraz x _i = x _i ( q ¹ , q ² , q ³ ) są funkcjami gładkimi (w sposób ciągły różniczkowalne), to współczynniki transformacji można zapisać jako i . Oznacza to, że stosunki te są pochodnymi cząstkowymi współrzędnych należących do jednego układu względem współrzędnych należących do drugiego układu. ${\ Displaystyle {\ cfrac {\ częściowy q ^ {i}} {\ częściowy x_ {j}}}}$${\ Displaystyle {\ cfrac {\ częściowy x_ {i}} {\ częściowy q ^ {j}}}}$

Konstruowanie bazy kowariantnej w trzech wymiarach

Robiąc to samo dla współrzędnych w pozostałych 2 wymiarach, b ₁ można wyrazić jako:

${\ Displaystyle \ mathbf {b} _ {1} = p ^ {1} \ mathbf {e} _ {1} + p ^ {2} \ mathbf {e} _ {2} + p ^ {3} \ mathbf {e} _{3}={\cfrac {\częściowy x_{1}}{\częściowy q^{1}}}\mathbf {e} _{1}+{\cfrac {\częściowy x_{2}} {\częściowe q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\częściowe q^{1}}}\mathbf {e} _{3} }$

Podobne równania obowiązują dla b ₂ i b _{3 ,} więc standardowa baza { e ₁ , e ₂ , e ₃ } jest przekształcana w lokalną (uporządkowaną i znormalizowaną ) bazę { b ₁ , b ₂ , b ₃ } przez następujący układ równania:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {b} _ {1} i = {\ cfrac {\ częściowy x_ {1}} {\ częściowy q ^ {1}}} \ mathbf {e} _ {1} +{\cfrac {\partial x_{2}}{\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1 }}}\mathbf {e} _{3}\\\mathbf {b} _{2}&={\cfrac {\partial x_{1}}{\partial q^{2}}}\mathbf {e } _{1}+{\cfrac {\częściowy x_{2}}{\częściowy q^{2}}}\mathbf {e} _{2}+{\cfrac {\częściowy x_{3}}{\ częściowe q^{2}}}\mathbf {e} _{3}\\\mathbf {b} _{3}&={\cfrac {\partial x_{1}}{\częściowe q^{3}} }\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{3}}}\mathbf {e} _{2}+{\cfrac {\partial x_{ 3}}{\częściowe q^{3}}}\mathbf {e} _{3}\end{wyrównane}}}$

Poprzez analogiczne rozumowanie można uzyskać odwrotną transformację bazy lokalnej do bazy standardowej:

${\ Displaystyle {\ zacząć {wyrównany} \ mathbf {e} _ {1} i = {\ cfrac {\ częściowy q ^ {1}} {\ częściowy x_ {1}}} \ mathbf {b} _ {1} +{\cfrac {\partial q^{2}}{\partial x_{1}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{1 }}}\mathbf {b} _{3}\\\mathbf {e} _{2}&={\cfrac {\częściowe q^{1}}{\częściowe x_{2}}}\mathbf {b } _{1}+{\cfrac {\częściowe q^{2}}{\częściowe x_{2}}}\mathbf {b} _{2}+{\cfrac {\częściowe q^{3}}{ \partial x_{2}}}\mathbf {b} _{3}\\\mathbf {e} _{3}&={\cfrac {\partial q^{1}}{\partial x_{3}} }\mathbf {b} _{1}+{\cfrac {\częściowy q^{2}}{\częściowy x_{3}}}\mathbf {b} _{2}+{\cfrac {\częściowy q^ {3}}{\częściowy x_{3}}}\mathbf {b} _{3}\end{wyrównany}}}$

Jakobian transformacji

Powyższe układy równań liniowych można zapisać w postaci macierzowej stosując konwencję sumowania Einsteina jako

${\ Displaystyle {\ cfrac {\ częściowy x_ {i}} {\ częściowy q ^ {k}}} \ mathbf {e} _ {i} = \ mathbf {b} _ {k}, \ quad {\ cfrac { \partial q^{i}}{\partial x_{k}}}\mathbf {b} _{i}=\mathbf {e} _{k}}$.

Ta macierz współczynników układu liniowego jest macierzą Jakobianu (i jego odwrotnością) transformacji. Są to równania, których można użyć do przekształcenia bazy kartezjańskiej w bazę krzywoliniową i odwrotnie.

W trzech wymiarach rozwinięte formy tych macierzy są

${\ Displaystyle \ mathbf {J} = {\ zacząć {bmatrix} {\ cfrac {\ częściowy x_ {1}} {\ częściowy q ^ {1}}} i {\ cfrac {\ częściowy x_ {1}} {\ częściowe q^{2}}}&{\cfrac {\partial x_{1}}{\partial q^{3}}}\\{\cfrac {\partial x_{2}}{\partial q^{1 }}}&{\cfrac {\partial x_{2}}{\partial q^{2}}}&{\cfrac {\partial x_{2}}{\partial q^{3}}}\\{ \cfrac {\partial x_{3}}{\partial q^{1}}}&{\cfrac {\partial x_{3}}{\partial q^{2}}}&{\cfrac {\partial x_ {3}}{\częściowa q^{3}}}\\\end{bmacierz}},\quad \mathbf {J} ^{-1}={\begin{bmacierz}{\cfrac {\częściowa q^ {1}}{\partial x_{1}}}&{\cfrac {\partial q^{1}}{\partial x_{2}}}&{\cfrac {\partial q^{1}}{\ częściowe x_{3}}}\\{\cfrac {\partial q^{2}}{\partial x_{1}}}&{\cfrac {\partial q^{2}}{\partial x_{2} }}&{\cfrac {\częściowy q^{2}}{\częściowy x_{3}}}\\{\cfrac {\częściowy q^{3}}{\częściowy x_{1}}}&{\ cfrac {\częściowy q^{3}}{\częściowy x_{2}}}&{\cfrac {\częściowy q^{3}}{\częściowy x_{3}}}\\\end{bmacierz}}}$

W transformacji odwrotnej (układ drugiego równania) niewiadomymi są krzywoliniowe wektory bazowe. Dla każdej określonej lokalizacji może istnieć tylko jeden i tylko jeden zbiór wektorów bazowych (w przeciwnym razie baza nie jest dobrze zdefiniowana w tym punkcie). Warunek ten jest spełniony wtedy i tylko wtedy, gdy układ równań ma jedno rozwiązanie. W algebrze liniowej układ równań liniowych ma jedno rozwiązanie (nietrywialne) tylko wtedy, gdy wyznacznik jego macierzy układu jest niezerowy:

${\ Displaystyle \ det (\ mathbf {J} ^ {-1}) \ neq 0}$

co pokazuje uzasadnienie powyższego wymogu dotyczącego odwrotnego wyznacznika jakobianu.

Uogólnienie do n wymiarów

Formalizm rozciąga się na dowolny skończony wymiar w następujący sposób.

Rozważmy rzeczywistego euklidesowej n wymiarową przestrzeń, to R ⁿ = R x R x ... x R ( n razy), w którym R jest zestaw z liczb rzeczywistych , a x oznacza iloczyn , która jest przestrzenią liniową .

W współrzędnych tej przestrzeni może być oznaczona: x = ( x ₁ , x ₂ , ..., x _n ). Ponieważ jest to wektor (element przestrzeni wektorowej), można go zapisać jako:

${\ Displaystyle \ mathbf {x} = \ suma _ {i = 1} ^ {n} x_ {i} \ mathbf {e} ^ {i}}$

gdzie e ¹ = (1,0,0...,0), e ² = (0,1,0...,0), e ³ = (0,0,1...,0),. .., e ⁿ = (0,0,0...,1) jest standardowym zbiorem bazowym wektorów dla przestrzeni R ⁿ , a i = 1, 2,... n jest składowymi etykietowania indeksu. Każdy wektor ma dokładnie jedną składową w każdym wymiarze (lub "osi") i są one wzajemnie ortogonalne ( prostopadłe ) i znormalizowane (ma jednostkę wielkości ).

Mówiąc bardziej ogólnie, możemy zdefiniować wektory bazowe b _i tak, że zależą od q = ( q ₁ , q ₂ ,..., q _n ), tj. zmieniają się od punktu do punktu: b _i = b _i ( q ). W takim przypadku zdefiniować ten sam punkt x w kategoriach tej alternatywnej bazy: współrzędne w odniesieniu do tej bazy v _i również koniecznie zależą od x , to znaczy v _i = v _i ( x ). Wtedy wektor v w tej przestrzeni, z uwzględnieniem tych alternatywnych współrzędnych i wektorów bazowych, można rozwinąć jako kombinację liniową w tej bazie (co oznacza po prostu pomnożenie każdego wektora bazowego e _i przez liczbę v _i – mnożenie przez skalar ):

${\ Displaystyle \ mathbf {v} = \ suma _ {j = 1} ^ {n} {\ bar {v}} ^ {j} \ mathbf {b} _ {j} = \ suma _ {j = 1} ^{n}{\bar {v}}^{j}(\mathbf {q} )\mathbf {b} _{j}(\mathbf {q} )}$

Suma wektorowa opisująca v w nowej bazie składa się z różnych wektorów, chociaż sama suma pozostaje taka sama.

Transformacja współrzędnych

Z bardziej ogólnej i abstrakcyjnej perspektywy, krzywoliniowy układ współrzędnych jest po prostu łatą współrzędnych na rozmaitości różniczkowej E ⁿ (n-wymiarowa przestrzeń euklidesowa ), która jest dyfeomorficzna z kartezjańską łatą na rozmaitości. Dwie dyfeomorficzne łatki współrzędnych na rozmaitości różniczkowej nie muszą nakładać się w sposób zróżnicowany. Przy tej prostej definicji krzywoliniowego układu współrzędnych wszystkie poniższe wyniki są po prostu zastosowaniami standardowych twierdzeń w topologii różniczkowej .

Funkcje transformacji są takie, że istnieje relacja jeden-do-jednego między punktami w "starych" i "nowych" współrzędnych, to znaczy, że te funkcje są bijekcje i spełniają następujące wymagania w swoich dziedzinach :

Algebra wektorów i tensorów w trójwymiarowych współrzędnych krzywoliniowych

Uwaga: poniżej zastosowano konwencję sumowania Einsteina dotyczącą sumowania na powtarzających się indeksach.

Elementarna algebra wektorów i tensorów we współrzędnych krzywoliniowych jest używana w starszej literaturze naukowej z zakresu mechaniki i fizyki i może być niezbędna do zrozumienia prac z początku i połowy XX wieku, na przykład tekstu Greena i Zerny. W tej sekcji podano kilka przydatnych relacji w algebrze wektorów i tensorów drugiego rzędu we współrzędnych krzywoliniowych. Notacja i treść pochodzą głównie od Ogdena, Naghdi, Simmondsa, Greena i Zerny, Basara i Weicherta oraz Ciarleta.

Tensory we współrzędnych krzywoliniowych

Tensor drugiego rzędu można wyrazić jako

${\ Displaystyle {\ boldsymbol {S}} = S ^ {ij} \ mathbf {b} _ {i} \ otimes \ mathbf {b} _ {j} = S ^ {i} _ {j} \ mathbf {b} _{i}\otimes \mathbf {b} ^{j}=S_{i}{}^{j}\mathbf {b} ^{i}\otimes \mathbf {b} _{j}= S_{ij}\mathbf {b} ^{i}\otimes \mathbf {b} ^{j}}$

gdzie oznacza iloczyn tensorowy . Komponenty S ^ij nazywamy składowymi kontrawariantnymi , S ⁱ _j – mieszanymi składowymi prawostronnie kowariantnymi , S _i ^j – mieszanymi składowymi lewostronnie kowariantnymi , a S _ij – składowymi kowariantnymi tensora drugiego rzędu. Składniki tensora drugiego rzędu są powiązane przez ${\ Displaystyle \ scriptstyle \ czasami}$

${\ Displaystyle S ^ {ij} = g ^ {ik} S_ {k} ^ {j} = g ^ {jk} S ^ {i} {} _ {k} = g ^ {ik} g ^ { j\ell }S_{k\ell }}$

Tensor metryczny w ortogonalnych współrzędnych krzywoliniowych

Na każdym etapie można skonstruować niewielką część linii d x , zatem kwadratowy długości elementu liniowego jest iloczyn skalarny d x • d x i jest nazywana metryką w przestrzeni , ze wzoru:

${\ Displaystyle d \ mathbf {x} \ cdot d \ mathbf {x} = {\ cfrac {\ częściowy x_ {i}} {\ częściowy q ^ {j}}} {\ cfrac {\ częściowy x_ {i}} {\częściowe q^{k}}}dq^{j}dq^{k}}$.

Następna część powyższego równania

${\ Displaystyle {\ cfrac {\ częściowy x_ {k}} {\ częściowy q ^ {i}}} {\ cfrac {\ częściowy x_ {k}} {\ częściowy q ^ {j}}} = g_ {ij} (q^{i},q^{j})=\mathbf {b} _{i}\cdot \mathbf {b} _{j}}$

jest symetryczny tensor nazywany podstawowym (lub metryczny) tensor w przestrzeni euklidesowej w krzywoliniowych współrzędnych.

Indeksy można podnosić i obniżać za pomocą metryki:

${\ Displaystyle v ^ {i} = g ^ {ik} v_ {k}}$

Związek ze współczynnikami Lamé

Definiowanie współczynników skali h _i przez

${\ Displaystyle h_ {i} h_ {j} = g_ {ij} = \ mathbf {b} _ {i} \ cdot \ mathbf {b} _ {j} \ quad \ Rightarrow \ quad h_ {i} = {\ sqrt {g_{ii}}}=\left|\mathbf {b} _{i}\right|=\left|{\cfrac {\częściowy \mathbf {x} }{\częściowy q^{i}}} \prawo|}$

daje związek między tensorem metrycznym a współczynnikami Lamé, a

${\ Displaystyle g_ {ij} = {\ cfrac {\ częściowy \ mathbf {x}} {\ częściowy q ^ {i}}} \ cdot {\ cfrac {\ częściowy \ mathbf {x}} {\ częściowy q ^ { j}}}=\left(h_{ki}\mathbf {e} _{k}\right)\cdot \left(h_{mj}\mathbf {e} _{m}\right)=h_{ki} h_{kj}}$

gdzie h _ij są współczynnikami Lamé. Dla bazy ortogonalnej mamy również:

${\ Displaystyle g = g_ {11} g_ {22} g_ {33} = h_ {1} ^ {2} h_ {2} {2} h_ {3} ^ {2} \ quad \ Rightarrow \ quad {\ sqrt {g}}=h_{1}h_{2}h_{3}=J}$

Przykład: współrzędne biegunowe

Jeśli weźmiemy pod uwagę współrzędne biegunowe dla R ² ,

${\displaystyle (x,y)=(r\cos\theta,r\sin \theta)}$

(r, θ) to współrzędne krzywoliniowe, a jakobian wyznacznik przekształcenia ( r ,θ) → ( r cos θ, r sin θ) to r .

W ortogonalne wektory bazowe są b _R = (cos θ sin θ) b _θ = (R sin θ r cos θ). Współczynnikami skali są h _r = 1 i h _θ = r . Podstawowym tensorem jest g ₁₁ =1, g ₂₂ = r ² , g ₁₂ = g ₂₁ =0.

Tensor naprzemienny

W ortonormalnej prawoskrętnej podstawie tensor przemienny trzeciego rzędu jest zdefiniowany jako

${\ Displaystyle {\ boldsymbol {\ mathcal {e}}} = \ varepsilon _ {ijk} \ mathbf {e} ^ {i} \ otimes \ mathbf {e} ^ {j} \ otimes \ mathbf {e} ^ { k}}$

W ogólnej bazie krzywoliniowej ten sam tensor można wyrazić jako

${\ Displaystyle {\ boldsymbol {\ mathcal {e}}} = {\ mathcal {e}} _ {ijk} \ mathbf {b} ^ {i} \ otimes \ mathbf {b} ^ {j} \ otimes \ mathbf {b} ^{k}={\mathcal {E}}^{ijk}\mathbf {b} _{i}\otimes \mathbf {b} _{j}\otimes \mathbf {b} _{k} }$

Można też wykazać, że

${\ Displaystyle {\ mathcal {E}} ^ {ijk} = {\ cfrac {1} {J}} \ varepsilon _ {ijk} = {\ cfrac {1} {+ {\ sqrt {g}}}}} varepsilon _{ijk}}$

Symbole Christoffela

Symbole Christoffel pierwszego rodzaju${\ Displaystyle \ Gamma _ {kij}}$

${\ Displaystyle \ mathbf {b} _ {i, j} = {\ Frac {\ częściowy \ mathbf {b} _ {i}} {\ częściowy q ^ {j}}} = \ mathbf {b} ^ {k }\Gamma _{kij}\quad \Rightarrow \quad \mathbf {b} _{k}\cdot \mathbf {b} _{i,j}=\Gamma _{kij}}$

gdzie przecinek oznacza pochodną cząstkową (patrz rachunek Ricciego ). Aby wyrazić Γ _kij w postaci g _ij ,

${\ Displaystyle {\ zacząć {wyrównany} g_ {ij, k} & = (\ mathbf {b} _ {i} \ cdot \ mathbf {b} _ {j}) _ {, k} = \ mathbf {b} _{i,k}\cdot \mathbf {b} _{j}+\mathbf {b} _{i}\cdot \mathbf {b} _{j,k}=\Gamma _{jik}+\Gamma _{ijk}\\g_{ik,j}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}=\mathbf {b} _{i ,j}\cdot \mathbf {b} _{k}+\mathbf {b} _{i}\cdot \mathbf {b} _{k,j}=\Gamma _{kij}+\Gamma _{ikj }\\g_{jk,i}&=(\mathbf {b} _{j}\cdot \mathbf {b} _{k})_{,i}=\mathbf {b} _{j,i} \cdot \mathbf {b} _{k}+\mathbf {b} _{j}\cdot \mathbf {b} _{k,i}=\Gamma _{kji}+\Gamma _{jki}\end {wyrównany}}}$

Od

${\ Displaystyle \ mathbf {b} _ {i, j} = \ mathbf {b} _ {j, i} \ quad \ Rightarrow \ quad \ Gamma _ {kij} = \ Gamma _ {kji}}$

użycie ich do zmiany powyższych relacji daje

${\ Displaystyle \ Gamma _ {kij} = {\ Frac {1} {2}} (g_ {ik, j} + g_ {jk, i} - g_ {ij, k}) = {\ Frac {1} { 2}}[(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}+(\mathbf {b} _{j}\cdot \mathbf {b} _ {k})_{,i}-(\mathbf {b} _{i}\cdot \mathbf {b} _{j})_{,k}]}$

Symbole Christoffel drugiego rodzaju${\ Displaystyle \ Gamma ^ {k} {} _ {ji}}$

${\ Displaystyle \ Gamma ^ {k} {} _ {ij} = g ^ {kl} \ Gamma _ {lij} = \ Gamma ^ {k} {} _ {ji} \ quad {\ cfrac {\ częściowy \ mathbf {b} _{i}}{\częściowy q^{j}}}=\mathbf {b} _{k}\Gamma ^{k}{}_{ij}}$

To daje do zrozumienia ze

${\ Displaystyle \ Gamma ^ {k} {} _ {ij} = {\ cfrac {\ częściowy \ mathbf {b} _ {i}} {\ częściowy q ^ {j}}} \ cdot \ mathbf {b} ^ {k}=-\mathbf {b} _{i}\cdot {\cfrac {\częściowy \mathbf {b} ^{k}}{\częściowy q^{j}}}\quad }$od .${\ Displaystyle \ quad {\ cfrac {\ częściowy} {\ częściowy q ^ {j}}} (\ mathbf {b} _ {i} \ cdot \ mathbf {b} ^ {k}) = 0}$

Inne relacje, które następują, to:

${\ Displaystyle {\ cfrac {\ częściowy \ mathbf {b} ^ {i}} \ częściowy q ^ {j}}} = - \ Gamma ^ {i} {} _ {jk} \ mathbf {b} ^ { k},\quad {\boldsymbol {\nabla }}\mathbf {b} _{i}=\Gamma ^{k}{}_{ij}\mathbf {b} _{k}\otimes \mathbf {b } ^{j},\quad {\boldsymbol {\nabla }}\mathbf {b} ^{i}=-\Gamma ^{i}{}_{jk}\mathbf {b} ^{k}\otimes \mathbf {b} ^{j}}$

Operacje na wektorach

Rachunek wektorowy i tensorowy w trójwymiarowych współrzędnych krzywoliniowych

Uwaga: poniżej zastosowano konwencję sumowania Einsteina dotyczącą sumowania na powtarzających się indeksach.

W obliczeniach całek liniowych , powierzchniowych i objętościowych należy wprowadzić poprawki . Dla uproszczenia, poniższe ogranicza się do trzech wymiarów i ortogonalnych współrzędnych krzywoliniowych. Jednak te same argumenty dotyczą przestrzeni n- wymiarowych. Gdy układ współrzędnych nie jest ortogonalny, w wyrażeniach występują dodatkowe terminy.

Simmonds w swojej książce o analizie tensorowej cytuje wypowiedź Alberta Einsteina :

Magia tej teorii z pewnością narzuci się każdemu, kto naprawdę ją zrozumiał; reprezentuje prawdziwy triumf metody absolutnego rachunku różniczkowego, stworzonej przez Gaussa, Riemanna, Ricciego i Levi-Civita.

Rachunek wektorowy i tensorowy w ogólnych współrzędnych krzywoliniowych jest używany w analizie tensorowej na czterowymiarowych rozmaitościach krzywoliniowych w ogólnej teorii względności , w mechanice zakrzywionych powłok , w badaniu właściwości niezmienniczych równań Maxwella, które są przedmiotem zainteresowania metamateriałów i wielu innych dziedzin .

W tej sekcji podano kilka przydatnych relacji w rachunku wektorów i tensorów drugiego rzędu we współrzędnych krzywoliniowych. Notacja i treść pochodzą głównie od Ogdena, Simmondsa, Greena i Zerny, Basara i Weicherta oraz Ciarleta.

Niech φ = φ( x ) będzie dobrze zdefiniowanym polem skalarnym i v = v ( x ) dobrze zdefiniowanym polem wektorowym, a λ ₁ , λ ₂ ... będą parametrami współrzędnych

Elementy geometryczne

Integracja

Operator	Pole skalarne	Pole wektorowe
Całka liniowa	${\ Displaystyle \ int _ {C} \ varphi (\ mathbf {x}) ds = \ int _ {a} ^ {b} \ varphi (\ mathbf {x} (\ lambda)) \ lewo | {\ częściowy \ mathbf {x} \over \częściowa \lambda}\right|d\lambda }$	${\ Displaystyle \ int _ {C} \ mathbf {v} (\ mathbf {x}) \ cdot d \ mathbf {s} = \ int _ {a} ^ {b} \ mathbf {v} (\ mathbf {x } (\lambda ))\cdot \left({\partial \mathbf {x} \over \partial \lambda }\right)d\lambda }$
Całka powierzchniowa	${\ Displaystyle \ int _ {S} \ varphi (\ mathbf {x} ) dS = \ iint _ {T} \ varphi (\ mathbf {x} (\ lambda _ {1}, \ lambda _ {2})) \left|{\partial \mathbf {x} \over \partial \lambda _{1}}\times {\partial \mathbf {x} \over \partial \lambda _{2}}\right|d\lambda _ {1}d\lambda _{2}}$	${\ Displaystyle \ int _ {S} \ mathbf {v} (\ mathbf {x}) \ cdot ds = \ iint _ {T} \ mathbf {v} (\ mathbf {x} (\ lambda _ {1}, \lambda _{2}))\cdot \left({\partial \mathbf {x} \over \partial \lambda _{1}}\times {\partial \mathbf {x} \over \partial \lambda _{ 2}}\right)d\lambda _{1}d\lambda _{2}}$
Całka objętości	${\ Displaystyle \ iint _ {V} \ varphi (x, y, z) dV = \ iint _ {V} \ chi (q_ {1}, q_ {2}, q_ {3}) Jdq_ {1} dq_ { 2}dq_{3}}$	${\ Displaystyle \ iint _ {V} \ mathbf {u} (x, y, z) dV = \ iint _ {V} \ mathbf {v} (q_ {1}, q_ {2}, q_ {3}) Jdq_{1}dq_{2}dq_{3}}$

Różnicowanie

Wyrażenia dla gradientu, dywergencji i Laplace'a można bezpośrednio rozszerzyć do n- wymiarów, jednak rotacja jest zdefiniowana tylko w 3D.

Pole wektorowe b _i jest styczne do krzywej współrzędnych q ⁱ i tworzy naturalną podstawę w każdym punkcie krzywej. Ta podstawa, jak omówiono na początku tego artykułu, jest również nazywana kowariantną podstawą krzywoliniową. Możemy również zdefiniować bazę odwrotną lub kontrawariantną bazę krzywoliniową, b ⁱ . Wszystkie relacje algebraiczne między wektorami bazy, omówione w rozdziale o algebrze tensorów, dotyczą bazy naturalnej i jej odwrotności w każdym punkcie x .

Operator	Pole skalarne	Pole wektorowe	Pole tensora drugiego rzędu
Gradient	${\ Displaystyle \ nabla \ varphi = {\ cfrac {1} {h_ {i}}} {\ częściowy \ varphi \ nad \ częściowy q ^ {i}} \ mathbf {b} ^ {i}}$	${\ Displaystyle \ nabla \ mathbf {v} = {\ cfrac {1} {h_ {i} ^ {2}}} {\ częściowy \ mathbf {v} \ ponad \ częściowy q ^ {i}} \ otimes \ mathbf {b} _{i}}$	${\ Displaystyle {\ boldsymbol {\ nabla}} {\ boldsymbol {S}} = {\ cfrac {\ częściowy {\ boldsymbol {S}}} {\ częściowy q ^ {i}}} \ czasami \ mathbf {b} ^{i}}$
Rozbieżność	Nie dotyczy	${\ Displaystyle \ nabla \ cdot \ mathbf {v} = {\ cfrac {1} {\ prod _ {j} h_ {j}}} {\ Frac {\ częściowy} {\ częściowy q ^ {i}}} ( v^{i}\prod _{j\neq i}h_{j})}$	${\ Displaystyle ({\ pogrubienie {\ nabla}} \ cdot {\ pogrubienie {S}}) \ cdot \ mathbf {a} = {\ pogrubienie {\ nabla}} \ cdot ({\ pogrubienie {S}} \ cdot \mathbf {a} )}$ gdzie a jest dowolnym stałym wektorem. We współrzędnych krzywoliniowych ${\ Displaystyle {\ boldsymbol {\ nabla}} \ cdot {\ boldsymbol {S}} = \ lewo [{\ cfrac {\ częściowy S_ {ij}} {\ częściowy q ^ {k}}} - \ Gamma _ { ki}^{l}S_{lj}-\Gamma _{kj}^{l}S_{il}\right]g^{ik}\mathbf {b} ^{j}}$
Laplace'a	${\ Displaystyle \ nabla ^ {2} \ varphi = {\ cfrac {1} {\ prod _ {j} h_ {j}}} {\ Frac {\ częściowy} {\ częściowy q ^ {i}}} \ lewo ({\cfrac {\prod _{j}h_{j}}{h_{i}^{2}}}{\frac {\częściowy \varphi }{\częściowy q^{i}}}\right)}$
Kędzior	Nie dotyczy	Tylko dla pól wektorowych w 3D, ${\ Displaystyle \ nabla \ razy \ mathbf {v} = {\ Frac {1} {h_ {1} h_ {2} h_ {3}}} \ mathbf {e} _ {i} \ epsilon _ {ijk} h_ {i}{\frac {\częściowy (h_{k}v_{k})}{\częściowy q^{j}}}}$ gdzie jest symbol Levi-Civita . ${\ Displaystyle \ epsilon _ {ijk}}$	Zobacz Zawinięcie pola tensorowego