Dwuścienna symetria w trzech wymiarach - Dihedral symmetry in three dimensions

Grupy punktów w trzech wymiarach

Symetria inwolucyjna C s , (*) [] =	Cykliczna symetria C nv , (* nn) [n] =	Symetria dwuścienna D nh , (* n22) [n, 2] =
Grupa wielościenna , [n, 3], (* n32)
Symetria czworościenna T d , (* 332) [3,3] =	Symetria ośmiościenna O h , (* 432) [4,3] =	Symetria ikozaedryczna I h , (* 532) [5,3] =

W geometrii , dwuścienny symetrii w trzech wymiarach, jest jednym z trzech nieskończonych sekwencji grup punktów w trzech wymiarach , które mają grupę symetrii że streszczenie grupa jest dwuściennej grupy Dih _n (dla n  ≥ 2).

Rodzaje

Są 3 typy dwuściennej symetrii w trzech wymiarach, co przedstawiono poniżej w 3 postaciach: notacji Schönflies , notacja Coxeter i notacji Orbifold .

Chiralny

• D _n , [ n , 2] ⁺ , (22 n ) rzędu 2 n - symetria dwuścienna lub grupa para-n-gonalna (grupa abstrakcyjna: Dih _n ).

Achiral

• D _nh , [ n , 2], (* 22 n ) rzędu 4 n - symetria pryzmatyczna lub pełna grupa ortogonalna (grupa abstrakcyjna: Dih _n × Z ₂ ).
• D _nd (lub D _nv ), [2 n , 2 ⁺ ], (2 * n ) rzędu 4 n - symetria antypryzmatyczna lub pełna grupa żyroskopowo-gonalna (grupa abstrakcyjna: Dih _{2 n} ).

Dla danego n , wszystkie trzy n -krotnie symetrię obrotową wokół osi ( obrót o kąt 360 ° / n nie zmienia obiektu) i 2-krotną symetrią obrotową wokół osi pionowej, a tym samym o n z nich. Dla n = ∞ odpowiadają one trzem grupom Frieze . Stosowana jest notacja Schönflies , z notacją Coxetera w nawiasach i notacją orbifold w nawiasach. Termin pozioma (h) jest używany w odniesieniu do pionowej osi obrotu.

W 2D grupa symetrii D _n obejmuje odbicia w liniach. Gdy płaszczyzna 2D jest osadzona poziomo w przestrzeni 3D, takie odbicie można postrzegać albo jako ograniczenie do tej płaszczyzny odbicia przez płaszczyznę pionową, albo jako ograniczenie do płaszczyzny obrotu wokół linii odbicia o 180 °. °. W 3D rozróżnia się dwie operacje: grupa D _n zawiera tylko obroty, a nie odbicia. Druga grupa to symetria piramidalna C _nv tego samego rzędu, 2 n .

Przy symetrii odbicia w płaszczyźnie prostopadłej do n- krotnej osi obrotu otrzymujemy D _nh , [n], (* 22 n ).

D _nd (lub D _nv ), [2 n , 2 ⁺ ], (2 * n ) ma pionowe lustrzane płaszczyzny między poziomymi osiami obrotu, a nie przez nie. W wyniku tego, oś pionowa jest 2- n -krotnie rotoreflection osi.

D _NH jest grupa symetrii regularnych n -sided graniastosłupa , jak również regularną n jednostronne podwójnej piramidy . D _II jest grupa symetrii regularnych n -sided antygraniastosłup , a także o regularnej n jednostronne trapezohedron . D _n jest grupą symetrii częściowo obróconego pryzmatu.

n  = 1 nie jest uwzględniane, ponieważ trzy symetrie są równe innym:

• D ₁ i C ₂ : grupa rzędu 2 z jednym obrotem o 180 °.
• D _{1 h} i C _{2 v} : grupa rzędu 4 z odbiciem w płaszczyźnie i obróceniem o 180 ° wokół linii w tej płaszczyźnie.
• D _{1 d} i C _{2 h} : grupa rzędu 4 z odbiciem w płaszczyźnie i obróceniem o 180 ° wokół linii prostopadłej do tej płaszczyzny.

Dla n  = 2 nie ma jednej osi głównej i dwóch dodatkowych osi, ale są trzy równoważne.

• D ₂ , [2,2] ⁺ , (222) rzędu 4 jest jednym z trzech typów grup symetrii z czterema grupami Kleina jako grupą abstrakcyjną. Posiada trzy prostopadłe 2-krotne osie obrotu. Jest to grupa symetrii prostopadłościanu z literą S na dwóch przeciwległych ścianach, w tej samej orientacji.
• D _{2 h} , [2,2], (* 222) rzędu 8 jest grupą symetrii prostopadłościanu.
• D _{2 d} , [4,2 ⁺ ], (2 * 2) rzędu 8 to grupa symetrii np .:
  • Kwadratowy prostopadłościan z przekątną narysowaną na jednej kwadratowej powierzchni i prostopadłą przekątną na drugiej.
  • Regularny czworościan przeskalowany w kierunku linii łączącej punkty środkowe dwóch przeciwległych krawędzi ( D _{2 d} jest podgrupą T _d ; skalując zmniejszamy symetrię).

Podgrupy

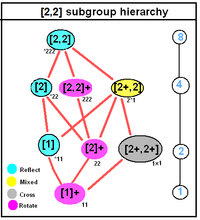D 2h , [2,2], (* 222)

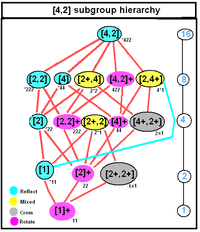D 4h , [4,2], (* 224)

Dla D _nh , [n, 2], (* 22n), zamów 4n

• C _nh , [n ⁺ , 2], (n *), rząd 2n
• C _nv , [n, 1], (* nn), zamówienie 2n
• D _n , [n, 2] ⁺ , (22n), rząd 2n

Dla D _nd , [2n, 2 ⁺ ], (2 * n), zamów 4n

• S _{2 n} , [2n ⁺ , 2 ⁺ ], (n ×), rząd 2n
• C _nv , [n ⁺ , 2], (n *), rząd 2n
• D _n , [n, 2] ⁺ , (22n), rząd 2n

D _nd jest również podgrupą D _{2 nh} .

Przykłady

D 2h , [2,2], (* 222) Zamówienie 8	D 2d , [4,2 + ], (2 * 2) Rząd 8	D 3h , [3,2], (* 223) Zarządzenie 12
ścieżki do koszykówki	ścieżki szwów baseballowych (ignorowanie kierunkowości szwu)	Piłka plażowa (ignorowanie kolorów)

D _nh , [ n ], (* 22 n ):

pryzmaty

D _{5 h} , [5], (* 225):

Pryzmat pentagramowy

Pentagramowy antypryzmat

D _{4 d} , [8,2 ⁺ ], (2 * 4):

Snub kwadratowy antypryzmat

D _{5 d} , [10,2 ⁺ ], (2 * 5):

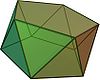Pięciokątny antypryzmat

Pentagrammic cross-antiprism

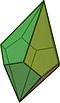pięciokątny trapez

D _{17 d} , [34,2 ⁺ ], (2 * 17):

Sześciokątny antypryzmat

Zobacz też

• Lista sferycznych grup symetrii
• Grupy punktów w trzech wymiarach
• Cykliczna symetria w trzech wymiarach

Bibliografia

• Coxeter , HSM i Moser, WOJ (1980). Generatory i relacje dla grup dyskretnych . Nowy Jork: Springer-Verlag. ISBN   0-387-09212-9 . CS1 maint: wiele nazw: lista autorów ( link )
• NW Johnson : Geometries and Transformations , (2018) ISBN   978-1-107-10340-5 Rozdział 11: Skończone grupy symetrii , 11.5 Sferyczne grupy Coxetera
• Conway, John Horton ; Huson, Daniel H. (2002), „The Orbifold Notation for Two-Dimensional Groups”, Structural Chemistry , Springer Netherlands, 13 (3): 247–257, doi : 10.1023 / A: 1015851621002

Linki zewnętrzne

• Graficzny przegląd 32 krystalograficznych grup punktów - tworzą pierwsze części (poza pominięciem n = 5) 7 nieskończonych serii i 5 z 7 oddzielnych grup punktów 3D