Twierdzenie o wartości pośredniej - Intermediate value theorem

Twierdzenie o wartości pośredniej: Niech f będzie funkcją ciągłą określoną na [ a , b ] i niech s będzie liczbą z f ( a ) < s < f ( b ). Wtedy istnieje jakieś x między a i b takie, że f ( x ) = s .

W analizy matematycznej The wartości pośredniej twierdzenie , że jeśli f jest ciągłą funkcję których domena zawiera interwał [ , b ] , a następnie przybiera danej wartości pomiędzy f ( ) i f ( b ) w pewnym momencie w przedziale .

Ma to dwa ważne następstwa :

1. Jeśli funkcja ciągła ma wartości przeciwnego znaku wewnątrz przedziału, to ma pierwiastek w tym przedziale ( twierdzenie Bolzano ).
2. Obraz funkcji ciągłej nad przerwą jest sam odstęp.

Motywacja

Twierdzenie o wartości pośredniej

Przechwytuje to intuicyjną własność funkcji ciągłych po liczbach rzeczywistych : przy danej f ciągłej na [1, 2] ze znanymi wartościami f (1) = 3 i f (2) = 5, a następnie wykres y = f ( x ) musi przechodzić przez poziomą linię y  = 4, podczas gdy x przechodzi od 1 do 2. Przedstawia to ideę, że wykres funkcji ciągłej na przedziale domkniętym można narysować bez podnoszenia ołówka z kartki.

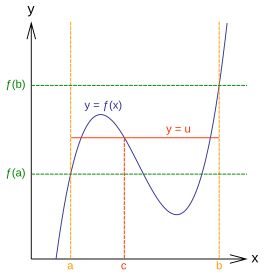
Twierdzenie

Twierdzenie o wartości pośredniej brzmi następująco:

Rozważmy przedział liczb rzeczywistych i funkcję ciągłą . Następnie ${\ Displaystyle I = [a, b]}$${\ Displaystyle \ mathbb {R}}$${\ Displaystyle f \ dwukropek I \ do \ mathbb {R}}$

• Wersja I. if jest liczbą pomiędzy a , czyli${\ Displaystyle u}$${\displaystyle f(a)}$${\ Displaystyle f (b)}$
  $${\displaystyle \min(f(a),f(b))<u<\max(f(a),f(b)),}$$

  
  to jest taki, że .${\displaystyle c\in (a,b)}$${\ Displaystyle f (c) = u}$
• Wersja II. zestaw obraz jest również przerwa i zawiera ,${\ Displaystyle f (I)}$${\ Displaystyle {\ bigl [} \ min (f (a), f (b)), \ max (f (a), f (b)) {\ duży ]}}$

Uwaga: Wersja II stwierdza, że zbiór wartości funkcji nie ma przerw. Dla dowolnych dwóch wartości funkcji , nawet jeśli znajdują się poza przedziałem między a , wszystkie punkty w przedziale są również wartościami funkcji, ${\displaystyle c<d}$${\displaystyle f(a)}$${\ Displaystyle f (b)}$${\displaystyle {\bigl [}c,d{\duży ]}}$

${\displaystyle {\bigl [}c,d{\duży]}\subseteq f(I)}$.

Podzbiór liczb rzeczywistych bez wewnętrznej przerwy to przedział. Wersja I jest naturalnie zawarta w wersji II .

Stosunek do kompletności

Twierdzenie zależy od zupełności liczb rzeczywistych i jest jej równoważne . Twierdzenie o wartości pośredniej nie ma zastosowania do liczb wymiernych Q, ponieważ między liczbami wymiernymi istnieją przerwy; Liczby niewymierne wypełniają te luki. Na przykład, funkcja dla spełnia i . Jednak nie ma takiej liczby wymiernej , że , ponieważ jest liczbą niewymierną. ${\ Displaystyle f (x) = x ^ {2}-2}$${\ Displaystyle x \ w \ mathbb {Q}}$${\ Displaystyle f (0) = -2}$${\ Displaystyle f(2) = 2}$${\displaystyle x}$${\ Displaystyle f (x) = 0}$${\displaystyle {\sqrt {2}}}$

Dowód

Twierdzenie to można udowodnić jako konsekwencję własności zupełności liczb rzeczywistych w następujący sposób:

Udowodnimy pierwszy przypadek, . Drugi przypadek jest podobny. ${\displaystyle f(a)<u<f(b)}$

Niech będzie zbiorem wszystkich takich, które . Wtedy jest niepuste, ponieważ jest elementem . Ponieważ jest niepuste i ograniczone powyżej przez , przez zupełność, supremum istnieje. Oznacza to, że jest to najmniejsza liczba, która jest większa lub równa każdemu członkowi . Twierdzimy, że . ${\displaystyle S}$${\displaystyle x\in [a,b]}$${\displaystyle f(x)\leq u}$${\displaystyle S}$${\displaystyle a}$${\displaystyle S}$${\displaystyle S}$${\displaystyle b}$ ${\displaystyle c=\sup S}$${\displaystyle c}$${\displaystyle S}$${\ Displaystyle f (c) = u}$

Napraw trochę . Ponieważ jest ciągły, istnieje taki, że kiedykolwiek . To znaczy że ${\ Displaystyle \ varepsilon > 0}$${\displaystyle f}$${\ Displaystyle \ delta > 0}$${\ Displaystyle | f (x)-f (c) | <\ varepsilon }$${\displaystyle |xc|<\delta}$

${\displaystyle f(x)-\varepsilon <f(c)<f(x)+\varepsilon}$

dla wszystkich . Dzięki właściwościom supremum istnieje coś, co jest zawarte w , a więc ${\displaystyle x\in (c-\delta,c+\delta)}$${\ Displaystyle a ^ {*} \ w (c-\ delta, c]}$${\displaystyle S}$

${\ Displaystyle f (c) < f (a ^ {*}) + \ varepsilon \ leq u + \ varepsilon }$.

Zbieranie , wiemy o tym , ponieważ jest supremum . To znaczy że ${\ Displaystyle a ^ {**} \ w (c, c + \ delta)}$${\ Displaystyle a ^ {**} \ nie \ w S}$${\displaystyle c}$${\displaystyle S}$

${\ Displaystyle f (c)> f (a ^ {**}) - \ varepsilon \ > u- \ varepsilon}$.

Obie nierówności

${\displaystyle u-\varepsilon <f(c)<u+\varepsilon}$

są ważne dla wszystkich , z których dedukujemy jako jedyną możliwą wartość, jak stwierdzono. ${\ Displaystyle \ varepsilon > 0}$${\ Displaystyle f (c) = u}$

Uwaga: Twierdzenie o wartości pośredniej można również udowodnić za pomocą metod analizy niestandardowej , która stawia „intuicyjne” argumenty dotyczące nieskończenie małych na rygorystycznej podstawie.

Historia

Twierdzenie to zostało po raz pierwszy udowodnione przez Bernarda Bolzano w 1817 roku. Bolzano użył następującego sformułowania twierdzenia:

Niech będą funkcjami ciągłymi na przedziale między i takim, że i . Potem jest między i takie, że . ${\displaystyle f,\phi}$${\ Displaystyle \ alfa}$${\ Displaystyle \ beta}$${\displaystyle f(\alfa )<\phi (\alfa)}$${\displaystyle f(\beta)>\phi (\beta)}$${\displaystyle x}$${\ Displaystyle \ alfa}$${\ Displaystyle \ beta}$${\ Displaystyle f (x) = \ phi (x)}$

Równoważność między tym sformułowaniem a współczesnym można wykazać, ustawiając odpowiednią funkcję stałą. Augustin-Louis Cauchy dostarczył nowoczesnego sformułowania i dowodu w 1821 roku. Obaj inspirowali się celem sformalizowania analizy funkcji i pracą Josepha-Louisa Lagrange'a . Pomysł, że funkcje ciągłe posiadają właściwość wartości pośredniej, ma wcześniejsze pochodzenie. Simon Stevin udowodnił twierdzenie o wartości pośredniej dla wielomianów ( na przykładzie liczby sześciennej ), dostarczając algorytm do konstruowania rozwinięcia dziesiętnego rozwiązania. Algorytm iteracyjnie dzieli interwał na 10 części, tworząc dodatkową cyfrę dziesiętną na każdym kroku iteracji. Zanim podano formalną definicję ciągłości, w definicji funkcji ciągłej podano właściwość wartości pośredniej. Zwolennikami jest Louis Arbogast , który założył, że funkcje nie mają skoków, spełniają właściwość wartości pośredniej i mają przyrosty, których rozmiary odpowiadają rozmiarom przyrostów zmiennej. Wcześniejsi autorzy utrzymywali, że wynik jest intuicyjnie oczywisty i nie wymaga dowodu. Intuicja Bolzano i Cauchy'ego polegała na zdefiniowaniu ogólnego pojęcia ciągłości (w kategoriach nieskończenie małych w przypadku Cauchy'ego i wykorzystaniu rzeczywistych nierówności w przypadku Bolzano) oraz dostarczeniu dowodu opartego na takich definicjach. ${\displaystyle \phi}$

Uogólnienia

Twierdzenie o wartości pośredniej jest ściśle związane z topologicznym pojęciem spójności i wynika z podstawowych własności zbiorów spójnych w przestrzeniach metrycznych, a w szczególności spójnych podzbiorów R :

• Jeśli i są przestrzeniami metrycznymi , jest mapą ciągłą i jest połączonym podzbiorem, to jest połączony. (*)${\ Displaystyle X}$${\ Displaystyle Y}$${\ Displaystyle f \ dwukropek X \ do Y}$${\ Displaystyle E \ podzbiór X}$${\ Displaystyle f (E)}$
• Podzbiór jest połączony wtedy i tylko wtedy, gdy spełnia następującą właściwość: . (**)${\ Displaystyle E \ podzbiór \ mathbb {R}}$${\displaystyle x,y\w e,\ x<r<y\implikuje r\w e}$

W rzeczywistości powiązanie jest właściwością topologiczną i (*) uogólnia na przestrzenie topologiczne : Jeśli i są przestrzeniami topologicznymi, jest ciągłą mapą i jest przestrzenią spójną , to jest połączone. ${\ Displaystyle X}$${\ Displaystyle Y}$${\ Displaystyle f \ dwukropek X \ do Y}$${\ Displaystyle X}$${\displaystyle f(X)}$ Zachowanie powiązań przy odwzorowaniach ciągłych można traktować jako uogólnienie twierdzenia o wartości pośredniej, własności funkcji o wartościach rzeczywistych zmiennej rzeczywistej, na funkcje ciągłe w przestrzeniach ogólnych.

Przypomnijmy pierwszą wersję twierdzenia o wartości pośredniej, opisaną wcześniej:

Twierdzenie o wartości pośredniej jest bezpośrednią konsekwencją tych dwóch właściwości powiązania:

Twierdzenie o wartości pośredniej uogólnia się w naturalny sposób: Załóżmy, że X jest spójną przestrzenią topologiczną, a ( Y , <) jest całkowicie uporządkowanym zbiorem wyposażonym w topologię porządku i niech f  : X → Y będzie odwzorowaniem ciągłym. Jeśli i b są dwa punkty X i U jest punktem T leży między f ( ) i f ( b ) w odniesieniu do <, to istnieje C w X takich, że f ( c ) =  u . Oryginalne twierdzenie jest odzyskiwane przez zauważenie, że R jest połączone i że jego naturalną topologią jest topologia porządku.

Twierdzenie Brouwera o punkcie stałym jest pokrewnym twierdzeniem, które w jednym wymiarze daje szczególny przypadek twierdzenia o wartości pośredniej.

Converse to fałsz

Funkcja Darboux jest funkcją o wartościach rzeczywistych f, która ma „właściwość wartości pośredniej”, tj. spełnia wniosek twierdzenia o wartości pośredniej: dla dowolnych dwóch wartości a i b w dziedzinie f i dowolnej y pomiędzy f ( a ) i f ( b ) jest trochę c między a i b , gdzie f ( c ) = y . Twierdzenie o wartości pośredniej mówi, że każda funkcja ciągła jest funkcją Darboux. Jednak nie każda funkcja Darboux jest ciągła; tzn. odwrotność twierdzenia o wartości pośredniej jest fałszywa.

Jako przykład weźmy funkcję f  : [0, ∞) → [−1, 1] zdefiniowaną przez f ( x ) = sin(1/ x ) dla x  > 0 i f (0) = 0. Ta funkcja nie jest ciągła w x  = 0, ponieważ ograniczenie stanowi f ( x ), a x ma tendencję do 0 ° C, nie istnieje; jednak funkcja ma właściwość wartości pośredniej. Inny, bardziej skomplikowany przykład podaje funkcja Conway'a o podstawie 13 .

W rzeczywistości twierdzenie Darboux mówi, że wszystkie funkcje, które wynikają z różniczkowania jakiejś innej funkcji na pewnym przedziale, mają właściwość wartości pośredniej (chociaż nie muszą być ciągłe).

Historycznie rzecz biorąc, ta właściwość wartości pośredniej była sugerowana jako definicja ciągłości funkcji o wartościach rzeczywistych; definicja ta nie została przyjęta.

Praktyczne zastosowania

Podobnym wynikiem jest twierdzenie Borsuka-Ulama , które mówi, że ciągła mapa od -sfery do -przestrzeni euklidesowej zawsze odwzorowuje parę antypodów na to samo miejsce. ${\ Displaystyle n}$${\ Displaystyle n}$

Na ogół dla każdej funkcji ciągłej, której domena jest zamknięty wypukłą część wymiarową kształt i każda litera wewnątrz kształtki (niekoniecznie jego centrum), istnieją dwa punkty antypodyczne w odniesieniu do danego punktu, którego wartość funkcjonalna jest taka sama. ${\ Displaystyle n}$

Twierdzenie to również stanowi podstawę wyjaśnienia, dlaczego obracanie chwiejnego stołu spowoduje jego stabilność (z zastrzeżeniem pewnych łatwych do spełnienia ograniczeń).

Zobacz też

• Twierdzenie o wartości średniej  – O istnieniu stycznej do łuku równoległego do prostej przechodzącej przez jej punkty końcowe
• Miara nieatomowa
• Twierdzenie o włochatej kuli  – sfery parzystowymiarowe nie mają niezerowych ciągłych pól wektorowych stycznych

Bibliografia

Zewnętrzne linki

• Twierdzenie o wartości pośredniej w ProofWiki
• Twierdzenie o wartości pośredniej - Twierdzenie Bolzano przy przecięciu węzła
• Twierdzenie Bolzano autorstwa Julio Cesar de la Yncera, Wolfram Demonstrations Project .
• Weisstein, Eric W. „Twierdzenie o wartości pośredniej” . MatematykaŚwiat .
• Belk, Jim (2 stycznia 2012). „Dwuwymiarowa wersja twierdzenia o wartości pośredniej” . Wymiana stosu .
• Dowód systemu Mizar : http://mizar.org/version/current/html/topreal5.html#T4