Matematyczne modelowanie chorób zakaźnych - Mathematical modelling of infectious disease

Modele matematyczne mogą rzutować postęp chorób zakaźnych, aby pokazać prawdopodobny wynik epidemii i pomóc w informowaniu o interwencjach w zakresie zdrowia publicznego . Modele wykorzystują podstawowe założenia lub zebrane statystyki wraz z matematyką, aby znaleźć parametry dla różnych chorób zakaźnych i wykorzystują te parametry do obliczania skutków różnych interwencji, takich jak programy masowych szczepień . Modelowanie może pomóc w podjęciu decyzji, których interwencji unikać, a których wypróbować, lub może przewidzieć przyszłe wzorce wzrostu itp.

Historia

Modelowanie chorób zakaźnych jest narzędziem wykorzystywanym do badania mechanizmów rozprzestrzeniania się chorób, przewidywania przyszłego przebiegu epidemii i oceny strategii kontrolowania epidemii.

Pierwszym naukowcem, który systematycznie próbował określić przyczyny zgonów, był John Graunt w swojej książce Natural and Political Observations dokonanych na temat rachunków za śmiertelność w 1662 roku. Rachunki, które badał, były wykazami liczb i przyczyn zgonów publikowanymi co tydzień. Analiza przyczyn zgonów dokonana przez Graunta jest uważana za początek „teorii rywalizujących zagrożeń”, która według Daleya i Ganiego jest „teorią, która jest obecnie dobrze ugruntowana wśród współczesnych epidemiologów”.

Najwcześniejsze sprawozdanie z matematycznego modelowania rozprzestrzeniania się choroby przeprowadził w 1760 r. Daniel Bernoulli . Z wykształcenia lekarz, Bernoulli stworzył model matematyczny do obrony praktyki szczepienia przeciwko ospie . Obliczenia z tego modelu wykazały, że uniwersalne szczepienie przeciwko ospie wydłużyłoby oczekiwaną długość życia z 26 lat 7 miesięcy do 29 lat 9 miesięcy. Prace Daniela Bernoulliego poprzedziły współczesne rozumienie teorii zarazków .

Na początku XX wieku William Hamer i Ronald Ross zastosowali prawo masowego działania w celu wyjaśnienia zachowań epidemicznych.

W latach dwudziestych pojawiły się modele przedziałowe. Modelu Kermacka-McKendrick epidemia (1927) oraz modelu epidemia Reed-Frost (1928) opisują relacje między podatnych , zakażonych i immunologicznych osobników w populacji. Model epidemii Kermacka-McKendricka był skuteczny w przewidywaniu zachowania epidemii bardzo podobnego do obserwowanego w wielu zarejestrowanych epidemiach.

Ostatnio modele oparte na agentach (ABM) są używane w zamian za prostsze modele przedziałowe . Na przykład epidemiologiczne ABM są wykorzystywane do informowania o interwencjach w zakresie zdrowia publicznego (niefarmaceutycznych) przeciwko rozprzestrzenianiu się SARS-CoV-2 . Epidemiologiczne ABM, mimo swojej złożoności i wymagające dużej mocy obliczeniowej, były krytykowane za upraszczanie i nierealistyczne założenia. Mimo to mogą być przydatne w podejmowaniu decyzji dotyczących środków łagodzących i tłumiących w przypadkach, gdy ABM są dokładnie skalibrowane.

Założenia

Modele są tak dobre, jak założenia, na których są oparte. Jeśli model dokonuje prognoz, które są niezgodne z obserwowanymi wynikami, a matematyka jest poprawna, początkowe założenia muszą się zmienić, aby model był użyteczny.

• Rozkład wieku prostokątny i stacjonarny , tzn. wszyscy w populacji dożywają wieku L, a następnie umierają, a dla każdego wieku (do L ) jest taka sama liczba osób w populacji. Jest to często dobrze uzasadnione w krajach rozwiniętych, w których śmiertelność niemowląt jest niska, a znaczna część populacji dożywa średniej długości życia.
• Jednorodne mieszanie się populacji, tj. osobniki badanej populacji dobierają się i nawiązują losowo kontakt, a nie mieszają się przeważnie w mniejszej podgrupie. Założenie to rzadko jest uzasadnione, ponieważ struktura społeczna jest powszechna. Na przykład większość ludzi w Londynie kontaktuje się tylko z innymi londyńczykami. Co więcej, w Londynie istnieją mniejsze podgrupy, takie jak społeczność turecka lub nastolatki (żeby podać tylko dwa przykłady), które mieszają się ze sobą bardziej niż osoby spoza grupy. Jednak mieszanie homogeniczne jest standardowym założeniem, aby matematyka była wykonalna.

Rodzaje modeli epidemii

Stochastyczny

„Stochastyczny” oznacza bycie lub posiadanie zmiennej losowej. Model stochastyczny to narzędzie do szacowania rozkładów prawdopodobieństwa potencjalnych wyników poprzez umożliwienie losowej zmienności jednego lub większej liczby danych wejściowych w czasie. Modele stochastyczne zależą od prawdopodobnych zmian ryzyka ekspozycji, chorób i innych chorób. Statystyczne rozprzestrzenianie się choroby na poziomie czynnika w małych lub dużych populacjach można określić metodami stochastycznymi.

Deterministyczny

W przypadku dużych populacji, jak w przypadku gruźlicy, często stosuje się deterministyczne lub przedziałowe modele matematyczne. W modelu deterministycznym osobniki w populacji są przypisywane do różnych podgrup lub przedziałów, z których każdy reprezentuje określony etap epidemii.

Szybkości przejścia z jednej klasy do drugiej są matematycznie wyrażone jako pochodne, stąd model formułuje się za pomocą równań różniczkowych. Budując takie modele, należy założyć, że liczebność w przedziale jest zróżnicowana w czasie, a proces epidemii jest deterministyczny. Innymi słowy, zmiany w zaludnieniu przedziału można obliczyć tylko na podstawie historii, która została wykorzystana do opracowania modelu.

Numer reprodukcji

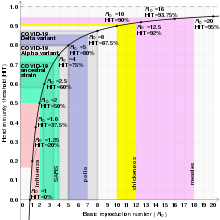
Podstawowe reprodukcją (oznaczonej przez R ₀ ) jest miarą tego, jak choroba jest przenoszona. Jest to średnia liczba osób, które jedna osoba zakaźna zarazi w trakcie swojej infekcji. Ta ilość określa, czy infekcja będzie się rozprzestrzeniać wykładniczo, wymierać, czy też pozostać na stałym poziomie: jeśli R ₀ > 1, to każda osoba zaraża średnio więcej niż jedną inną osobę, więc choroba się rozprzestrzeni; jeśli R ₀ < 1, to każda osoba zaraża średnio mniej niż jedną osobę, więc choroba wygaśnie; a jeśli R ₀ = 1, to każda osoba zakaże średnio dokładnie jedną osobę, więc choroba stanie się endemiczna: będzie się rozprzestrzeniać w całej populacji, ale nie będzie się zwiększać ani zmniejszać.

Endemiczny stan stacjonarny

Mówi się, że choroba zakaźna jest endemiczna, gdy może się utrzymywać w populacji bez konieczności angażowania środków zewnętrznych. Oznacza to, że średnio każda zarażona osoba zaraża dokładnie jedną inną osobę (im więcej, a liczba zarażonych będzie rosła wykładniczo i będzie epidemia , a jeszcze mniej i choroba umrze). W ujęciu matematycznym to jest:

${\ Displaystyle \ R_ {0}S \ =1.}$

Podstawowy numer reprodukcji ( R ₀ ) choroby, zakładając, że każdy jest podatny, pomnożonej przez część populacji, która jest faktycznie wrażliwe ( S ) musi być jeden (od tych, którzy nie są podatne nie funkcji w naszych obliczeń, ponieważ nie można zarazić się chorobą). Zauważ, że ta zależność oznacza, że ​​aby choroba była w endemicznym stanie stacjonarnym , im wyższa podstawowa liczba reprodukcji, tym mniejszy musi być odsetek populacji podatnej i odwrotnie. Wyrażenie to ma ograniczenia dotyczące proporcji podatności, np. R ₀ równe 0,5 implikuje S musi wynosić 2, jednak proporcja ta przekracza wielkość populacji.

Załóżmy prostokątny stacjonarny rozkład wieku i niech również wieki infekcji mają taki sam rozkład dla każdego roku urodzenia. Niech średni wiek infekcji wynosi A , na przykład gdy osoby młodsze niż A są podatne, a starsze niż A są odporne (lub zakaźne). Wtedy prostym argumentem można wykazać, że proporcja populacji, która jest podatna, wyraża się wzorem:

${\ Displaystyle S = {\ Frac {A} {L}}.}$

Powtarzamy, że L to wiek, w którym w tym modelu zakłada się, że umiera każda osoba. Ale matematyczną definicję endemicznego stanu ustalonego można zmienić, aby uzyskać:

${\ Displaystyle S = {\ Frac {1} {R_ {0}}}.}$

Dlatego ze względu na właściwość przechodnią :

${\ Displaystyle {\ Frac {1} {R_{0}}} = {\ Frac {A} {L}} \ Strzałka w prawo R_ {0} = {\ Frac {L} {A}}.}$

Zapewnia to prosty sposób oszacowania parametru R ₀ przy użyciu łatwo dostępnych danych.

Dla populacji o wykładniczym rozkładzie wieku ,

${\ Displaystyle R_ {0}=1+ {\ Frac {L} {A}}.}$

Pozwala to na określenie podstawowej liczby reprodukcji choroby podanej A i L w obu typach rozmieszczenia populacji.

Modele kompartmentowe w epidemiologii

Modele kompartmentowe są formułowane jako łańcuchy Markowa . Klasycznym modelem kompartmentowym w epidemiologii jest model SIR, który można wykorzystać jako prosty model do modelowania epidemii. Stosuje się również wiele innych typów modeli przedziałowych.

Model SIR

Schemat modelu SIR z wartościami początkowymi oraz współczynnikami infekcji i wyzdrowienia${\textstyle S(0)=997,I(0)=3,R(0)=0}$${\textstyle \beta =0.4}$${\textstyle \gamma =0,04}$

Animacja modelu SIR z wartościami początkowymi i wskaźnikiem odzysku . Animacja przedstawia efekt zmniejszenia wskaźnika infekcji z do . Jeśli nie są dostępne żadne lekarstwa lub szczepienia, możliwe jest zmniejszenie wskaźnika infekcji (często określanego jako „ spłaszczenie krzywej ”) poprzez odpowiednie środki, takie jak dystans społeczny.${\textstyle S(0)=997,I(0)=3,R(0)=0}$${\textstyle \gamma =0,04}$${\textstyle \beta =0.5}$${\textstyle \beta =0.12}$

W 1927 r. WO Kermack i AG McKendrick stworzyli model, w którym rozważali populację stałą z tylko trzema przedziałami: podatną, ; zainfekowany, ; i odzyskane, . Przegrody zastosowane w tym modelu składają się z trzech klas: ${\ Displaystyle S (t)}$${\ Displaystyle I (t)}$${\ Displaystyle R (t)}$

• ${\ Displaystyle S (t)}$ jest używany do reprezentowania osobników jeszcze niezakażonych chorobą w czasie t lub osobników podatnych na tę chorobę w populacji.
• ${\ Displaystyle I (t)}$ oznacza osobniki populacji, które zostały zakażone chorobą i są zdolne do rozprzestrzeniania choroby na osoby z kategorii podatnej.
• ${\ Displaystyle R (t)}$to przedział stosowany dla osobników populacji, którzy zostali zakażeni, a następnie usunięci z choroby, albo z powodu immunizacji, albo z powodu śmierci. Osoby należące do tej kategorii nie są w stanie ponownie zostać zainfekowane ani przenieść infekcji na inne osoby.

Inne modele komorowe

Istnieje wiele modyfikacji modelu SIR, w tym takie, które obejmują urodzenia i zgony, gdzie po wyzdrowieniu nie ma odporności (model SIS), gdzie odporność trwa tylko przez krótki okres czasu (SIRS), gdzie występuje okres utajony choroba, w której dana osoba nie jest zakaźna ( SEIS i SEIR ), i w której niemowlęta mogą urodzić się z odpornością (MSIR). W celu oceny progu epidemii w modelu SIS w sieciach patrz Parshani i in.

Dynamika choroby zakaźnej

Modele matematyczne muszą integrować rosnącą ilość danych generowanych na temat interakcji gospodarz - patogen . Wiele teoretyczne badania nad dynamiką populacji , struktury i ewolucji chorób zakaźnych z roślin i zwierząt, w tym ludzi, zajmują się tym problemem. Model do oceny prawdopodobieństwa rozprzestrzenienia się na całym świecie i ogłoszenia pandemii został niedawno opracowany przez Valdez et al. Tematy badawcze obejmują:

• Pandemia
• przenoszenie , rozprzestrzenianie się i kontrola infekcji
• sieci epidemiologiczne
• epidemiologia przestrzenna
• utrzymywanie się patogenów u gospodarzy
• dynamika wewnątrz hosta
• immuno -epidemiology
• zjadliwość
• Struktura szczepu (biologia) i interakcje
• przesunięcie antygenowe
• filodynamika
• genetyka populacji patogenów
• ewolucja i rozprzestrzenianie się oporu
• rola czynników genetycznych gospodarza
• narzędzia i innowacje statystyczne i matematyczne
• rola i identyfikacja rezerwuarów infekcji

Matematyka masowych szczepień

Jeżeli odsetek populacji, która jest uodporniona, przekracza poziom odporności stada na chorobę, choroba nie może dłużej utrzymywać się w populacji. Tak więc, jeśli ten poziom może zostać przekroczony przez szczepienie, choroba może zostać wyeliminowana. Przykładem udanego osiągnięcia tego na całym świecie jest globalna eradykacja ospy prawdziwej , z ostatnim dzikim przypadkiem w 1977 roku. WHO prowadzi podobną kampanię szczepień w celu wyeliminowania polio .

Poziom odporności stada będzie oznaczony q . Przypomnijmy, dla stabilnego stanu:

${\ Displaystyle R_ {0}\ cdot S = 1.}$

Z kolei,

${\ Displaystyle R_ {0}= {\ Frac {N} {S}} = {\ Frac {\ mu N \ nazwa operatora {E} (T_ {L})} {\ mu N \ nazwa operatora {E} [\ min (T_{L},T_{S})]}}={\frac {\nazwa operatora {E} (T_{L})}{\nazwa operatora {E} [\min(T_{L},T_{S} )]}},}$

czyli w przybliżeniu:

${\ Displaystyle {\ Frac {\ Operator {\ Operator {E} } (T_ {L})} {\ Operator {\ Operator {E}} (T_ {S})}} = 1 + {\ Frac {\ Lambda }{\mu }}={\frac {\beta N}{v}}.}$

Wykres progu odporności stada w funkcji podstawowej liczebności rozrodu z wybranymi chorobami

S będzie wynosić (1 −  q ), ponieważ q to odsetek populacji, która jest odporna, a q  +  S musi być równe jeden (ponieważ w tym uproszczonym modelu wszyscy są albo podatni, albo uodpornieni). Następnie:

${\ Displaystyle {\ zacząć {wyrównane} i R_ {0} \ cdot (1-q) = 1 \ \ [6pt] i 1-q = {\ Frac {1} {R_ {0}}} \ \ [6pt ]&q=1-{\frac {1}{R_{0}}}.\end{wyrównany}}}$

Pamiętaj, że to jest poziom progowy. Jeśli odsetek osób odpornych przekroczy ten poziom z powodu programu masowych szczepień, choroba wyginie.

Właśnie obliczyliśmy krytyczny próg immunizacji (oznaczony jako q _c ). Jest to minimalny odsetek populacji, który należy zaszczepić po urodzeniu (lub tuż przed narodzinami), aby zakażenie wymarło w populacji.

${\ Displaystyle q_ {c} = 1- {\ Frac {1} {R_ {0}}}.}$

Ponieważ ułamek ostatecznego rozmiaru populacji p, który nigdy nie jest zarażony, można zdefiniować jako:

${\ Displaystyle \ lim _ {t \ do \ infty} S (t) = e ^ {- \ int _ {0} ^ {\ infty} \ lambda (t) \ dt} = 1 p.}$

Stąd,

${\ Displaystyle p = 1-e ^ {- \ int _ {0} ^ {\ infty} \ beta I (t) \ dt} = 1-e ^ {-R_ {0} p}.}$

Rozwiązując dla , otrzymujemy: ${\displaystyle R_{0}}$

${\ Displaystyle R_ {0}= {\ Frac {- \ ln (1-p)} {p}}.}$

Kiedy masowe szczepienia nie mogą przekroczyć odporności stada

Jeśli zastosowana szczepionka jest niewystarczająco skuteczna lub nie można osiągnąć wymaganego pokrycia (np. z powodu popularnej oporności ), program może nie przekroczyć q _c . Taki program może jednak zaburzyć równowagę infekcji, nie eliminując jej, często powodując nieprzewidziane problemy.

Załóżmy, że część populacji q (gdzie q < q _c ) jest szczepiona zaraz po urodzeniu przeciwko infekcji R ₀  > 1. Program szczepień zmienia R ₀ na R _{q ,} gdzie

${\ Displaystyle R_ {q} = R_ {0}(1-q)}$

Ta zmiana następuje po prostu dlatego, że obecnie w populacji jest mniej podatnych na zakażenie. R _q to po prostu R ₀ minus te, które normalnie byłyby zakażone, ale teraz tak nie jest, ponieważ są odporne.

W konsekwencji tej niższej podstawowej liczby rozrodczości , średni wiek zarażenia A również zmieni się na pewną nową wartość A _q u tych, którzy nie zostali zaszczepieni.

Przypomnij sobie relację łączącą R ₀ , A i L . Zakładając, że średnia długość życia się nie zmieniła, teraz:

${\ Displaystyle R_ {q} = {\ Frac {L} {A_ {q}}}}$

${\ Displaystyle A_ {q} = {\ Frac {L} {R_ {q}}} = {\ Frac {L} {R_ {0}(1-q)}}.}$

Ale R ₀ = L / A więc:

${\ Displaystyle A_ {q} = {\ Frac {L} {(L/A) (1-q)}} = {\ Frac {AL} {L (1-q)}} = {\ Frac {A} {1-k}}.}$

W ten sposób program szczepień podniesie średni wiek infekcji, kolejne matematyczne uzasadnienie wyniku, który mógł być intuicyjnie oczywisty. Osoby nieszczepione doświadczają teraz zmniejszonej siły infekcji ze względu na obecność grupy zaszczepionej.

Jednak ważne jest, aby wziąć pod uwagę ten efekt podczas szczepienia przeciwko chorobom, które są cięższe u osób starszych. Program szczepień przeciwko takiej chorobie, który nie przekracza q _c, może spowodować więcej zgonów i powikłań niż było przed wprowadzeniem programu w życie, ponieważ ludzie będą zachorować na tę chorobę w późniejszym życiu. Te nieprzewidziane skutki programu szczepień nazywane są skutkami perwersyjnymi .

Kiedy masowe szczepienia przekraczają odporność stada

Jeśli program szczepień spowoduje, że odsetek odpornych osobników w populacji przekroczy próg krytyczny przez dłuższy czas, przenoszenie choroby zakaźnej w tej populacji zostanie zatrzymane. Jest to znane jako eliminacja infekcji i różni się od eradykacji .

Eliminacja

Przerwanie endemicznego przenoszenia choroby zakaźnej, które ma miejsce, gdy każdy zarażony osobnik zakaże mniej niż jednego drugiego, osiąga się poprzez utrzymanie zasięgu szczepień, aby utrzymać odsetek osób odpornych powyżej krytycznego progu immunizacji.

Likwidacja

Redukcja organizmów zakaźnych w środowisku naturalnym na całym świecie do zera. Do tej pory osiągnięto to tylko w przypadku ospy i księgosuszu . Aby dojść do wykorzenienia, należy osiągnąć eliminację we wszystkich regionach świata.

Niezawodność

Modele mają tę zaletę, że badają wiele wyników jednocześnie, zamiast tworzyć jedną prognozę. Modele wykazały szeroki stopień niezawodności w poprzednich pandemach, takich jak SARS , świńska grypa , MERS i Ebola .

Zobacz też

Bibliografia

Dalsza lektura

Zewnętrzne linki

Oprogramowanie

• Model-Builder : Interaktywne (oparte na GUI) oprogramowanie do budowania, symulacji i analizy modeli ODE.
• Symulator GLEaMviz : umożliwia symulację pojawiających się chorób zakaźnych rozprzestrzeniających się na całym świecie.
• STEM : Platforma open source do modelowania epidemiologicznego dostępna za pośrednictwem Eclipse Foundation.
• Nadzór nad pakietem R : Modelowanie czasowe i przestrzenno-czasowe oraz monitorowanie zjawisk epidemicznych