Liczba Pi - Pi

Liczba $π$ ( / p aɪ / ; napisana jako „ pi ”) jest stałą matematyczną , w przybliżeniu równą 3,14159. Jest ona zdefiniowana w geometrii euklidesowej jako wskaźnik z koła „S obwodu do jego średnicy , a także ma wiele równoważnych definicji. Liczba ta pojawia się w wielu wzorach we wszystkich dziedzinach matematyki i fizyki . Najwcześniejsze znane użycie greckiej litery π do oznaczenia stosunku obwodu koła do jego średnicy zostało użyte przez walijskiego matematyka Williama Jonesa w 1706 roku. Jest ona również określana jako stała Archimedesa .

Będąc liczbą niewymierną , $π$ nie może być wyrażona jako ułamek wspólny , chociaż ułamki takie jak22/7są powszechnie używane do przybliżania tego . Równoważnie jego reprezentacja dziesiętna nigdy się nie kończy i nigdy nie osadza się w stale powtarzającym się wzorze . Jego cyfry dziesiętne (lub inne podstawowe ) wydają się być rozmieszczone losowo i są przypuszczalnie spełniały określony rodzaj statystycznej losowości .

Wiadomo, że $π$ jest liczbą przestępną : nie jest pierwiastkiem żadnego wielomianu o współczynnikach wymiernych . Transcendencja $π$ oznacza, że nie da się rozwiązać starożytnego wyzwania kwadratury koła za pomocą cyrkla i linijki .

Starożytne cywilizacje, w tym Egipcjanie i Babilończycy , wymagały dość dokładnych przybliżeń $π$ do praktycznych obliczeń. Około 250 rpne grecki matematyk Archimedes stworzył algorytm przybliżający $π$ z arbitralną dokładnością. W 5 wieku naszej ery, chińskie matematyka przybliżeniu $π$ do siedmiu cyfr, a indyjskie matematyka popełnił pięciocyfrowy zbliżenia, zarówno przy użyciu technik geometrycznych. Pierwszy wzór obliczeniowy na $π$ , oparty na szeregach nieskończonych , został odkryty tysiąc lat później, kiedy szkołę astronomii i matematyki w Kerali odkryła serię Madhava-Leibniz , udokumentowaną w Yuktibhāṣā , napisanym około 1530 roku.

Wynalezienie rachunku różniczkowego wkrótce doprowadziło do obliczenia setek cyfr $π$ , co wystarczy do wszystkich praktycznych obliczeń naukowych. Niemniej jednak w XX i XXI wieku matematycy i informatycy zastosowali nowe podejścia, które w połączeniu ze wzrostem mocy obliczeniowej rozszerzyły dziesiętną reprezentację $π$ do wielu bilionów cyfr. Główną motywacją do tych obliczeń jest stworzenie przypadku testowego do opracowania wydajnych algorytmów do obliczania szeregów liczbowych, a także dążenie do bicia rekordów. Obszerne obliczenia wykorzystano również do testowania superkomputerów i bardzo precyzyjnych algorytmów mnożenia .

Ponieważ jego najbardziej elementarna definicja odnosi się do okręgu, $π$ występuje w wielu wzorach trygonometrii i geometrii , zwłaszcza tych dotyczących okręgów, elips i sfer. W bardziej nowoczesnej analizie matematycznej liczba jest zamiast tego definiowana przy użyciu właściwości spektralnych systemu liczb rzeczywistych , jako wartość własna lub okres , bez odniesienia do geometrii. Pojawia się zatem w dziedzinach matematyki i nauk ścisłych mających niewiele wspólnego z geometrią okręgów, takich jak teoria liczb i statystyka , a także w prawie wszystkich dziedzinach fizyki . Wszechobecność $π$ sprawia, że jest to jedna z najbardziej znanych stałych matematycznych — zarówno w środowisku naukowym, jak i poza nim. Opublikowano kilka książek poświęconych $π$ , a rekordowe obliczenia cyfr $π$ często skutkują nagłówkami prasowymi.

Podstawy

Nazwa

Symbolem używanym przez matematyków do przedstawienia stosunku obwodu koła do jego średnicy jest mała grecka litera $π$ , czasami zapisywana jako pi i wywodząca się z pierwszej litery greckiego słowa perimetros, oznaczającego obwód. W języku angielskim, $π$ jest wymawiane jako "pie" ( / p aɪ / PY ). W zastosowaniach matematycznych mała litera $π$ różni się od jej dużego i powiększonego odpowiednika $Π$ , który oznacza iloczyn ciągu , analogicznie do tego, jak $Σ$ oznacza sumowanie .

Wybór symbolu $π$ omówiono w rozdziale Przyjęcie symbolu $π$ .

Definicja

Obwód koła jest nieco ponad trzykrotnie dłuższy niż jego średnica. Dokładny stosunek nazywa się

π

.

$π$ jest powszechnie definiowany jako stosunek z koła jest obwód $C$ do jej średnicy $D$ :

{\ Displaystyle \ pi = {\ Frac {C} {d}}.}

Stosunek $C / d$ jest stały, niezależnie od wielkości koła. Na przykład, jeśli okrąg ma dwukrotnie większą średnicę niż inny okrąg, będzie również miał dwa razy większy obwód, zachowując stosunek $C / d$ . Ta definicja $π$ domyślnie wykorzystuje geometrię płaską (euklidesową) ; chociaż pojęcie okręgu można rozszerzyć na dowolną krzywą (nieeuklidesową) geometrię , te nowe okręgi nie będą już spełniać formuły $π = C / d$ .

Tutaj obwód koła jest długością łuku wokół obwodu koła, wielkością, którą można formalnie określić niezależnie od geometrii za pomocą granic — pojęcie w rachunku różniczkowym . Na przykład, można bezpośrednio obliczyć długość łuku górnej połowy okręgu jednostkowego, podaną we współrzędnych kartezjańskich równaniem $x 2 + y 2 = 1$ , jako całkę :

{\ Displaystyle \ pi = \ int _ {-1} ^ {1} {\ Frac {dx} {\ sqrt {1-x ^ {2}}}}}.

Całka taka jak ta została przyjęta jako definicja $π$ przez Karla Weierstrassa , który zdefiniował ją bezpośrednio jako całkę w 1841 roku.

Integracja nie jest już powszechnie stosowana w pierwszej definicji analitycznej, ponieważ, jak wyjaśnia Remmert 2012 , rachunek różniczkowy zwykle poprzedza rachunek całkowy w programie nauczania uniwersyteckiego, dlatego pożądane jest posiadanie definicji $π$ , która nie opiera się na tym ostatnim. Jedna z takich definicji, za sprawą Richarda Baltzera i spopularyzowana przez Edmunda Landaua , brzmi: $π$ to dwukrotność najmniejszej liczby dodatniej, przy której funkcja cosinus jest równa 0. Cosinus można zdefiniować niezależnie od geometrii jako szereg potęgowy lub jako rozwiązanie z równania różniczkowego .

W podobny ducha $π$ można określić na podstawie właściwości wykładniczą o wartościach zespolonych , $exp Z$ , o złożonej zmiennej $Z$ . Podobnie jak cosinus, wykładnik zespolony można zdefiniować na kilka sposobów. Zbiór liczb zespolonych, dla których $exp z$ jest równy jeden, jest więc (urojonym) ciągiem arytmetycznym postaci:

{\ Displaystyle \ {\ kropki, -2 \ pi ja, 0,2 \ pi ja, 4 \ pi ja, \ kropki \} = \ {2 \ pi ki \ średni k \ w \ mathbb {Z} \}}

i istnieje unikalna dodatnia liczba rzeczywista $π$ z tą własnością.

Bardziej abstrakcyjną odmianą tego samego pomysłu, wykorzystującą wyrafinowane matematyczne pojęcia topologii i algebry , jest następujące twierdzenie: istnieje unikalny ( aż do automorfizmu ) ciągły izomorfizm z grupy R / Z liczb rzeczywistych przy dodawaniu liczb całkowitych modulo ( grupa koła ), na przykład multiplikatywna grupa liczb zespolonych o bezwzględną wartość jeden. Liczba $π$ jest wtedy definiowana jako połowa wielkości pochodnej tego homomorfizmu.

Irracjonalność i normalność

$π$ jest liczbą niewymierną , co oznacza, że nie można jej zapisać jako ilorazu dwóch liczb całkowitych . Ułamki takie jak $22 / 7$ oraz $355 / 113$ są powszechnie używane do przybliżania $π$ , ale żaden wspólny ułamek (stosunek liczb całkowitych) nie może być jego dokładną wartością. Ponieważ $π$ jest irracjonalne, ma nieskończoną liczbę cyfr w reprezentacji dziesiętnej i nie układa się w nieskończenie powtarzający się wzór cyfr. Istnieje kilka dowodów na to, że $π$ jest irracjonalne ; na ogół wymagają rachunku różniczkowego i opierają się na technice reductio ad absurdum . Stopień, w jakim $π$ można aproksymować liczbami wymiernymi (zwanymi miarą irracjonalności ) nie jest dokładnie znany; Szacunki wykazały, że miara irracjonalności jest większa niż miara $e$ lub $ln 2,$ ale mniejsza niż miara liczb Liouville .

Cyfry $π$ nie mają widocznego wzoru i przeszły testy losowości statystycznej , w tym testy normalności ; liczba o nieskończonej długości nazywana jest normalną, gdy wszystkie możliwe ciągi cyfr (o dowolnej długości) pojawiają się równie często. Przypuszczenie, że $π$ jest normalne , nie zostało udowodnione ani obalone.

Od czasu pojawienia się komputerów dostępna jest duża liczba cyfr $π$ , na których można przeprowadzić analizę statystyczną. Yasumasa Kanada przeprowadził szczegółowe analizy statystyczne na cyfrach dziesiętnych $π$ i stwierdził, że są one zgodne z normalnością; na przykład częstości dziesięciu cyfr od 0 do 9 poddano testom istotności statystycznej i nie znaleziono dowodów na prawidłowość. Każdy losowy ciąg cyfr zawiera dowolnie długie podciągi, które wydają się nielosowe, zgodnie z twierdzeniem o nieskończonej małpie . Tak więc, ponieważ sekwencja cyfr $π$ przechodzi testy statystyczne na losowość, zawiera pewne sekwencje cyfr, które mogą wydawać się nielosowe, takie jak sekwencja sześciu kolejnych dziewiątek, która zaczyna się od 762. miejsca dziesiętnego reprezentacji $π$ . Jest to również nazywane „punktem Feynmana” w folklorze matematycznym , od nazwiska Richarda Feynmana , chociaż nie jest znany żaden związek z Feynmanem.

Transcendencja

Ponieważ

π

jest liczbą przestępną , kwadratura koła nie jest możliwa w skończonej liczbie kroków przy użyciu klasycznych narzędzi cyrkla i linijki .

Oprócz tego, że jest irracjonalna, $π$ jest również liczbą przestępną , co oznacza, że nie jest rozwiązaniem żadnego niestałego równania wielomianowego o współczynnikach wymiernych , takich jak $x 5 / 120 - x 3 / 6 + x = 0$ .

Transcendencja $π$ ma dwie ważne konsekwencje: Po pierwsze, $π$ nie można wyrazić za pomocą skończonej kombinacji liczb wymiernych i pierwiastków kwadratowych lub n -tych pierwiastków (takich jak $3 \sqrt 31$ lub $\sqrt 10$ ). Po drugie, ponieważ żadna liczba transcendentalna nie może być skonstruowana za pomocą kompasu i liniału mierniczego , nie jest możliwe „ podnieść do kwadratu okrąg ”. Innymi słowy, nie da się skonstruować za pomocą samego cyrkla i linijki kwadratu, którego pole jest dokładnie równe polu danego okręgu. Kwadratura koła była jednym z ważnych problemów geometrycznych klasycznej starożytności . Współcześni matematycy-amatorzy czasami próbowali kwadratury koła i twierdzić, że odniosą sukces — pomimo faktu, że jest to matematycznie niemożliwe.

Ułamki ciągłe

Zdjęcie greckiej litery pi, stworzonej jako duża kamienna mozaika zatopiona w ziemi.

Stała

π

jest reprezentowana na tej mozaice na zewnątrz budynku Matematyki na Politechnice Berlińskiej .

Podobnie jak wszystkie liczby niewymierne, $π$ nie może być reprezentowana jako ułamek pospolity (znany również jako ułamek prosty lub wulgarny ), z samej definicji liczby niewymiernej (tj. nie liczby wymiernej). Ale każda liczba niewymierna, w tym $π$ , może być reprezentowana przez nieskończoną serię zagnieżdżonych ułamków, zwaną ułamkiem ciągłym :

\pi=3+\textstyle {\cfrac{1}{7+\textstyle {\cfrac{1}{15+\textstyle {\cfrac{1}{1+\textstyle {\cfrac{1}{ 292+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{1+\ddots }}}}}}}}}}}} }

Obcięcie ułamka łańcuchowego w dowolnym punkcie daje racjonalne przybliżenie dla $π$ ; pierwsze cztery z nich to 3, 22/7, 333/106 i 355/113. Liczby te należą do najbardziej znanych i najczęściej używanych historycznych przybliżeń stałej. Każde przybliżenie wygenerowane w ten sposób jest najlepszym przybliżeniem racjonalnym; oznacza to, że każdy jest bliższy $π$ niż jakikolwiek inny ułamek o tym samym lub mniejszym mianowniku. Ponieważ wiadomo, że $π$ jest transcendentalne, z definicji nie jest algebraiczne, a więc nie może być kwadratowe irracjonalne . Dlatego $π$ nie może mieć okresowego ułamka łańcuchowego . Chociaż prosty ułamek ciągły dla $π$ (pokazany powyżej) również nie wykazuje żadnego innego oczywistego wzorca, matematycy odkryli kilka uogólnionych ułamków ciągłych, które mają, takie jak:

{\ Displaystyle {\ zacząć {wyrównany} \ pi & = \ textstyle {\ cfrac {4} {1 + \ textstyle {\ cfrac {1 ^ {2}} {2 + \ textstyle {\ cfrac {3 ^ {2} }{2+\textstyle {\cfrac {5^{2}}{2+\textstyle {\cfrac {7^{2}}{2+\textstyle {\cfrac {9^{2}}{2+\ ddots }}}}}}}}}}}=3+\textstyle {\cfrac {1^{2}}{6+\textstyle {\cfrac {3^{2}}{6+\textstyle {\ cfrac {5^{2}}{6+\textstyle {\cfrac {7^{2}}{6+\textstyle {\cfrac {9^{2}}{6+\ddots }}}}}}} }}}\\[8pt]&=\textstyle {\cfrac {4}{1+\textstyle {\cfrac {1^{2}}{3+\textstyle {\cfrac {2^{2}}{5 +\textstyle {\cfrac {3^{2}}{7+\textstyle {\cfrac {4^{2}}{9+\ddots }}}}}}}}}\end{wyrównany}}}

Przybliżona wartość i cyfry

Niektóre przybliżenia liczby pi obejmują:

Liczby całkowite : 3
Ułamki : przybliżone ułamki obejmują (w kolejności rosnącej dokładności)22/7, 333/106, 355/113, 52163/16604, 103993/33102, 104348/33215, oraz 245850922/78256779. (Lista jest wybranymi terminami z OEIS : A063674 i OEIS : A063673 .)
Cyfry : Pierwsze 50 cyfr dziesiętnych to 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510... (patrz OEIS : A000796 )

Cyfry w innych systemach liczbowych

Pierwsze 48 cyfr binarnych ( podstawa 2) (zwanych bitami ) to 11.0010 0100 0011 1111 0110 1010 1000 1000 1000 0101 1010 0011... (patrz OEIS : A004601 )
Pierwsze 20 cyfr w systemie szesnastkowym (podstawa 16) to 3.243F 6A88 85A3 08D3 1319... (patrz OEIS : A062964 )
Pierwsze pięć cyfr sześćdziesiętnych (podstawa 60) to 3;8,29,44,0,47 (patrz OEIS : A060707 )
Pierwsze 38 cyfr w trójskładnikowym systemie liczbowym to 10.010 211 0122 220 102 110 021 111 102 212 222 201... (patrz OEIS : A004602 )

Liczby zespolone i tożsamość Eulera

Związek między potęgami urojonymi liczby

e

a punktami na okręgu jednostkowym, którego środek znajduje się w punkcie początkowym na płaszczyźnie zespolonej określonej wzorem Eulera

Dowolną liczbę zespoloną , powiedzmy $z$ , można wyrazić za pomocą pary liczb rzeczywistych . W układzie współrzędnych biegunowych , numer jeden ( promień lub R ) stosuje się do oznaczenia $Z$ „S odległości od pochodzenia w płaszczyźnie zespolonej , a drugi kąt (lub $cp$ ) z lewoskrętnym obrót z dodatniej prostej:

{\ Displaystyle Z = r \ cdot (\ cos \ varphi + ja \ sin \ varphi ),}

gdzie $i$ jest jednostką urojoną spełniającą $i 2$ = -1. Częste występowanie $π$ w analizie zespolonej może być związane z zachowaniem funkcji wykładniczej zmiennej zespolonej, opisanej wzorem Eulera :

{\ Displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi,}

gdzie stała $e$ jest podstawą logarytmu naturalnego . Ta formuła ustala zgodność między urojonymi potęgami $e$ i punktami na okręgu jednostkowym, którego środek znajduje się na początku płaszczyzny zespolonej. Ustawienie $φ$ = $π$ we wzorze Eulera skutkuje tożsamością Eulera , celebrowaną w matematyce ze względu na to, że zawiera pięć najważniejszych stałych matematycznych:

{\ Displaystyle e ^ {i \ pi} +1 = 0.}

Istnieje $n$ różne liczby zespolone $z$ spełniających $z n = 1$ , a te są nazywane „ $n$ -tego korzenie jedności ” i oblicza się według wzoru:

{\ Displaystyle e ^ {2 \ pi IK / n} \ qquad (k = 0,1, 2, \ kropki, n-1).}

Historia

Antyk

Najbardziej znane przybliżenia datowania $π$ przed naszą erą były z dokładnością do dwóch miejsc po przecinku; poprawiono to w chińskiej matematyce, zwłaszcza w połowie pierwszego tysiąclecia, z dokładnością do siedmiu miejsc po przecinku. Od tego czasu nie poczyniono dalszych postępów aż do okresu późnego średniowiecza.

Na podstawie pomiarów Wielkiej Piramidy w Gizie (ok. 2560 pne) niektórzy egiptolodzy twierdzili, że starożytni Egipcjanie używali przybliżenia $π$ jako22/7już od Starego Państwa . Twierdzenie to spotkało się ze sceptycyzmem. Najwcześniejsze pisemne przybliżenia $π$ znajdują się w Babilonie i Egipcie, oba w zakresie jednego procenta prawdziwej wartości. W Babilonie gliniana tabliczka datowana na lata 1900–1600 p.n.e. zawiera geometryczne stwierdzenie, które w domyśle traktuje $π$ jako25/8 = 3,125. W Egipcie papirus Rhinda , datowany na około 1650 pne, ale skopiowany z dokumentu datowanego na 1850 pne, zawiera wzór na pole powierzchni koła, który traktuje $π$ jako (16/9) ² ≈ 3.16.

Obliczenia astronomiczne w Shatapatha Brahmana (ok. IV wpne) wykorzystują przybliżenie ułamkowe339/108 ≈ 3,139 (dokładność 9× ^10-4 ). Inne źródła indyjskie z około 150 rpne traktują $π$ jako $\sqrt 10$ ≈ 3,1622.

Epoka aproksymacji wielokątów

π

można oszacować, obliczając obwody opisanych i wpisanych wielokątów.

Pierwszym zarejestrowanym algorytmem rygorystycznego obliczania wartości $π$ było podejście geometryczne z użyciem wielokątów, opracowane około 250 rpne przez greckiego matematyka Archimedesa . Ten wielokątny algorytm dominował przez ponad 1000 lat, w wyniku czego $π$ jest czasami określany jako „stała Archimedesa”. Archimedes obliczył górną i dolną granicę $π$ , rysując sześciokąt foremny wewnątrz i na zewnątrz okręgu, a następnie podwajając liczbę boków, aż do osiągnięcia 96-bocznego wielokąta foremnego. Obliczając obwody tych wielokątów, udowodnił, że $223 / 71 < π < 22 / 7$ (czyli $3,1408 < π < 3,1429$ ). Górna granica Archimedesa z $22 / 7$ mogło doprowadzić do powszechnego przekonania, że $π$ jest równe $22 / 7$ . Około 150 rne grecko-rzymski naukowiec Ptolemeusz w swoim Almagest podał wartość $π$ 3,1416, którą mógł uzyskać od Archimedesa lub od Apoloniusza z Pergi . Matematycy używający algorytmów wielokątnych osiągnęli 39 cyfr $π$ w 1630 r., rekord pobity dopiero w 1699 r., kiedy użyto nieskończonych serii do osiągnięcia 71 cyfr.

Archimedes opracował wielokątne podejście do aproksymacji

π

.

W starożytnych Chinach wartości $π$ obejmowały 3,1547 (około 1 rne), $\sqrt 10$ (100 rne, około 3,1623) i $142 / 45$ (III wiek, około 3.1556). Około roku 265 ne matematyk Liu Hui z Wei Kingdom stworzył iteracyjny algorytm oparty na wielokątach i użył go z wielokątem o 3072 bokach, aby uzyskać wartość $π$ wynoszącą 3,1416. Później Liu wynalazł szybszą metodę obliczania $π$ i uzyskał wartość 3,14 dla wielokąta 96-bocznego, wykorzystując fakt, że różnice w polu kolejnych wielokątów tworzą szereg geometryczny o współczynniku 4. Chiński matematyk Zu Chongzhi około 480 rne obliczył, że $3,1415926 <$ $π$ $< 3,1415927$ i zasugerował przybliżenia $π$ $\approx$ $355 / 113$ = 3,14159292035... i $π \approx 22 / 7$ = 3,142857142857..., który nazwał odpowiednio Milü ("współczynnik bliskości") i Yuelü ("współczynnik przybliżony"), używając algorytmu Liu Hui zastosowanego do wielokąta o 12,288 bokach. Z prawidłową wartością dla jego siedmiu pierwszych miejsc po przecinku cyfr, ta wartość pozostała najdokładniejszym przybliżeniem $π$ dostępnym przez następne 800 lat.

Indyjski astronom Aryabhata w swojej Aryabhaṭiya (499 ne) użył wartości 3,1416 . Fibonacciego w ok. 1220 obliczono 3,1418 metodą wielokątną, niezależną od Archimedesa. Włoski autor Dante najwyraźniej zastosował wartość $3+ \sqrt 2 / 10 \approx 3.14142$ .

Perski astronom Jamshīd al-Kāshī wyprodukował 9 cyfr sześćdziesiętnych , mniej więcej odpowiednik 16 cyfr dziesiętnych, w 1424 roku, używając wielokąta o 3 x 2 ²⁸ bokach, co było rekordem świata przez około 180 lat. Francuski matematyk François Viète w 1579 roku uzyskał 9 cyfr z wielokątem o wymiarach 3×2 ¹⁷ boków. Flamandzki matematyk Adriaan van Roomen dotarł do 15 miejsc po przecinku w 1593 r. W 1596 r. holenderski matematyk Ludolph van Ceulen osiągnął 20 cyfr, rekord, który później zwiększył do 35 cyfr (w rezultacie $π$ nazywano w Niemczech „liczbą Ludolfia” do początek 20 wieku). Holenderski naukowiec Willebrord Snellius osiągnął 34 cyfry w 1621 roku, a austriacki astronom Christoph Grienberger osiągnął 38 cyfr w 1630 roku używając 10 ⁴⁰ boków. Christiaan Huygens był w stanie dotrzeć do 10 miejsc po przecinku w 1654 roku, używając nieco innej metody, odpowiadającej ekstrapolacji Richardsona .

Nieskończone serie

Porównanie zbieżności kilku historycznych nieskończonych szeregów dla

π

. S _n jest przybliżeniem po wzięciu n wyrazów. Każdy kolejny wykres podrzędny powiększa zacieniony obszar w poziomie 10 razy. (kliknij po szczegóły)

Obliczanie $π$ zostało zrewolucjonizowane przez rozwój technik serii nieskończonych w XVI i XVII wieku. Nieskończona seria jest sumą warunków nieskończonej sekwencji . Szeregi nieskończone pozwoliły matematykom obliczyć $π$ ze znacznie większą precyzją niż Archimedes i inni, którzy używali technik geometrycznych. Chociaż nieskończone serie były wykorzystywane do $π w$ szczególności przez europejskich matematyków, takich jak James Gregory i Gottfried Wilhelm Leibniz , podejście to zostało po raz pierwszy odkryte w Indiach między 1400 a 1500 rokiem n.e. Pierwszy pisemny opis nieskończonej serii, którą można wykorzystać do obliczenia $π,$ został przedstawiony w wersecie sanskryckim przez indyjskiego astronoma Nilakantha Somayaji w jego Tantrasamgraha , około 1500 roku n.e. Serie są prezentowane bez dowodów, ale dowody są przedstawione w późniejszym indyjskim dziele Yuktibhāṣā z około 1530 r. n.e. Nilakantha przypisuje serię wcześniejszemu indyjskiemu matematykowi, Madhavie z Sangamagmamy , który żył ok. 1930 roku. 1350 – ok. 1425. Opisano kilka nieskończonych szeregów, w tym szeregi dla sinusa, tangensa i cosinusa, które są obecnie określane jako szereg Madhavy lub szereg Gregory'ego-Leibniza . Madhava użył nieskończonych szeregów do oszacowania liczby $π$ do 11 cyfr około 1400, ale ta wartość została poprawiona do około 1430 przez perskiego matematyka Jamshīda al-Kāshī , używając algorytmu wielokątnego.

Oficjalny portret mężczyzny z długimi włosami

Isaac Newton użył nieskończonych szeregów do obliczenia

π

do 15 cyfr, później pisząc: „Wstyd mi powiedzieć, ile liczb przeprowadziłem te obliczenia”.

Pierwszy nieskończony ciąg odkryta w Europie był to produkt nieskończony (raczej niż nieskończona suma , która jest częściej używany w $gatunku$ obliczeń) znaleziony przez francuskiego matematyka François Viète w 1593 roku:

{\frac {2}{\pi}}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}} 2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots

Sekund nieskończony ciąg znaleźć w Europie , przez John Wallis w 1655 roku, była również produktem nieskończone:

{\frac {\pi}{2}}={\duży (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\duży)}\cdot { \Duża (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\duża )}\cdot {\duża (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\duża )}\cdot {\duża (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\duża )}\ cdoty

Odkrycie rachunku różniczkowego przez angielskiego naukowca Isaaca Newtona i niemieckiego matematyka Gottfrieda Wilhelma Leibniza w latach 60. XVII wieku doprowadziło do opracowania wielu nieskończonych szeregów do aproksymacji $π$ . Sam Newton użył szeregu arcsin do obliczenia 15-cyfrowego przybliżenia $π$ w 1665 lub 1666 roku, później pisząc: „Wstyd mi powiedzieć, ile cyfr wykonałem te obliczenia, nie mając w tym czasie żadnych innych spraw”.

W Europie formuła Madhavy została ponownie odkryta przez szkockiego matematyka Jamesa Gregory'ego w 1671 roku i przez Leibniza w 1674 roku:

{\ Displaystyle \ arctan z = z-{\ Frac {z ^ {3}} {3}} + {\ Frac {z ^ {5}} {5}} - {\ Frac {z ^ {7}} { 7}}+\cdots }

Ta formuła, seria Gregory'ego-Leibniza, równa się $π/4$ przy ocenie $z$ = 1. W 1699 roku angielski matematyk Abraham Sharp użył serii Gregory'ego-Leibniza do obliczenia $π$ do 71 cyfr, łamiąc poprzedni rekord 39 cyfr, co został ustawiony algorytmem wielokątnym. Reguła Gregory'ego-Leibniza dla szeregów jest prosta, ale zbiega się bardzo powoli (to znaczy stopniowo zbliża się do odpowiedzi), więc nie jest używana we współczesnych obliczeniach $π$ . ${\textstyle z={\frac {1}{\sqrt {3}}}}$ $z=1$

W 1706 John Machin użył serii Gregory'ego-Leibniza do stworzenia algorytmu, który zbiegał się znacznie szybciej:

{\frac {\pi}{4}}=4\arctan {\frac{1}{5}}-\arctan {\frac{1}{239}}.

Dzięki tej formule Machin osiągnął 100 cyfr $π$ . Inni matematycy stworzyli warianty, znane obecnie jako formuły podobne do Machin , które służyły do ustanawiania kilku kolejnych rekordów do obliczania cyfr $π$ . Formuły maszynopodobne pozostały najbardziej znaną metodą obliczania $π$ w epoce komputerów i były używane do ustanawiania rekordów przez 250 lat, których kulminacją było przybliżenie 620 cyfr w 1946 roku przez Daniela Fergusona – najlepsze przybliżenie osiągnięte bez pomocy urządzenia liczącego.

Rekord został ustanowiony przez cudownego wyrachowania Zachariasa Dase'a , który w 1844 r. na polecenie niemieckiego matematyka Carla Friedricha Gaussa wyliczył w swojej głowie formułę podobną do Machina, aby obliczyć 200 miejsc po przecinku $π$ w swojej głowie . Brytyjski matematyk William Shanks zajęło 15 lat, aby obliczyć od $π$ do 707 cyfr, ale popełnił błąd w 528. cyfrze, czyniąc wszystkie kolejne cyfry niepoprawnymi.

Wskaźnik konwergencji

Niektóre nieskończone szeregi dla $π$ zbiegają się szybciej niż inne. Mając do wyboru dwie nieskończone serie dla $π$ , matematycy będą na ogół używać tej, która zbiega szybciej, ponieważ szybsza zbieżność zmniejsza ilość obliczeń potrzebnych do obliczenia $π$ z dowolną określoną dokładnością. Prosty szereg nieskończony dla $π$ to szereg Gregory'ego-Leibniza :

{\ Displaystyle \ pi = {\ Frac {4}{1}} - {\ Frac {4} {3}} + {\ Frac {4} {5}} - {\ Frac {4} {7}} + {\frac {4}{9}}-{\frac {4}{11}}+{\frac {4}{13}}-\cdots }

Gdy poszczególne wyrazy tego nieskończonego szeregu są dodawane do sumy, suma stopniowo zbliża się do $π$ i – przy wystarczającej liczbie wyrazów – może zbliżyć się do $π,$ zgodnie z potrzebami. Zbiega się jednak dość powoli – po 500 000 wyrazów daje tylko pięć poprawnych cyfr dziesiętnych $π$ .

Nieskończony szereg dla $π$ (opublikowany przez Nilakantha w XV wieku), który zbiega się szybciej niż szereg Gregory'ego-Leibniza, to: Zauważ, że ( n − 1) n ( n + 1) = n ³ − n .

{\ Displaystyle \ pi = 3 + {\ Frac {4} {2 \ razy 3 \ razy 4}} - {\ Frac {4} {4 \ razy 5 \ razy 6}} + {\ Frac {4} {6 \times 7\times 8}}-{\frac {4}{8\times 9\times 10}}+\cdots }

W poniższej tabeli porównano współczynniki konwergencji tych dwóch szeregów:

Szeregi nieskończone dla $π$	Po I kadencji	Po II semestrze	Po III kadencji	Po 4 semestrze	Po 5 semestrze	Zbiega się do:
${\ Displaystyle \ pi = {\ Frac {4}{1}} - {\ Frac {4} {3}} + {\ Frac {4} {5}} - {\ Frac {4} {7}} + {\frac {4}{9}}-{\frac {4}{11}}+{\frac {4}{13}}+\cdots }$	4.0000	2,6666 ...	3.4666 ...	2.8952 ...	3.3396 ...	$π$ = 3,1415 ...
${\ Displaystyle \ pi = {3}+ {\ Frac {4}{2 \ razy 3 \ razy 4}} - {\ Frac {4} {4 \ razy 5 \ razy 6}} + {\ Frac {4} {6\times 7\times 8}}+\cdots }$	3.0000	3.1666 ...	3.1333 ...	3.1452 ...	3.1396 ...	$π$ = 3,1415 ...

Po pięciu kategoriach suma szeregu Gregory'ego-Leibniza mieści się w zakresie 0,2 prawidłowej wartości $π$ , podczas gdy suma szeregu Nilakantha mieści się w zakresie 0,002 prawidłowej wartości $π$ . Szereg Nilakanthy zbiega się szybciej i jest bardziej przydatny do obliczania cyfr $π$ . Szeregi, które zbiegają się jeszcze szybciej, obejmują szeregi Macina i Chudnovsky'ego , przy czym ten ostatni daje 14 poprawnych cyfr dziesiętnych na wyraz.

Irracjonalność i transcendencja

Nie wszystkie postępy matematyczne dotyczące $π$ miały na celu zwiększenie dokładności przybliżeń. Kiedy Euler rozwiązał problem bazylejski w 1735 r., znajdując dokładną wartość sumy odwrotnych kwadratów, ustalił związek między $π$ a liczbami pierwszymi, które później przyczyniły się do rozwoju i badania funkcji zeta Riemanna :

{\ Displaystyle {\ Frac {\ pi ^ {2}} {6}} = {\ Frac {1} {1 ^ {2}}} + {\ Frac {1} {2 ^ {2}}} + { \frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }

Szwajcarski naukowiec Johann Heinrich Lambert w 1761 udowodnił, że $π$ jest niewymierne , co oznacza, że nie jest równe ilorazowi dowolnych dwóch liczb całkowitych. Dowód Lamberta wykorzystywał ułamkową reprezentację funkcji stycznej. Francuski matematyk Adrien-Marie Legendre udowodnił w 1794 roku, że $π$ ² jest również nieracjonalne. W 1882 r. niemiecki matematyk Ferdinand von Lindemann udowodnił, że $π$ jest transcendentalne , potwierdzając przypuszczenie zarówno Legendre'a, jak i Eulera. Hardy i Wright stwierdzają, że „dowody zostały następnie zmodyfikowane i uproszczone przez Hilberta, Hurwitza i innych pisarzy”.

Przyjęcie symbolu $π$

Najwcześniejsze znane użycie greckiej litery $π$ do oznaczenia stosunku obwodu koła do jego średnicy zostało przez walijskiego matematyka Williama Jonesa w 1706 r.

Leonhard Euler spopularyzował użycie greckiej litery

π

w pracach opublikowanych w 1736 i 1748 roku.

W najwcześniejszych zastosowaniach grecka litera $π$ była skrótem od greckiego słowa oznaczającego peryferie ( περιφέρεια ) i była łączona w stosunkach z δ ( średnica ) lub ρ ( promień ) w celu utworzenia stałych okręgu. (Wcześniej matematycy używali zamiast tego liter takich jak c lub p .) Pierwszym odnotowanym użyciem jest „ ” Oughtreda , aby wyrazić stosunek obwodu i średnicy w 1647 i późniejszych wydaniach Clavis Mathematicae . Barrow również użył " " do reprezentowania stałej 3,14..., podczas gdy Gregory zamiast tego użył " " do reprezentowania 6,28... . $\delta.\pi$ ${\textstyle {\frac {\pi }{\delta }}}$ ${\textstyle {\frac {\pi }{\rho }}}$

Najwcześniejsze znane użycie samej greckiej litery $π$ do przedstawienia stosunku obwodu koła do jego średnicy zostało dokonane przez walijskiego matematyka Williama Jonesa w jego pracy z 1706 roku Synopsis Palmariorum Matheseos ; lub Nowe Wprowadzenie do Matematyki . Grecka litera pojawia się tam po raz pierwszy w wyrażeniu „1/2 peryferii ( $π$ )” w omówieniu koła o promieniu jeden. Pisze jednak, że jego równania na $π$ pochodzą z „gotowego pióra naprawdę genialnego pana Johna Machina ”, co prowadzi do spekulacji, że Machin mógł posługiwać się grecką literą przed Jonesem. Notacja Jonesa nie została natychmiast przyjęta przez innych matematyków, a notacja ułamkowa wciąż była używana dopiero w 1767 roku.

Euler zaczął używać jednoliterowej formy, zaczynając od swojego eseju wyjaśniającego właściwości powietrza z 1727 r. , chociaż w tym i kilku późniejszych pismach używał $π$ = 6,28... , stosunku obwodu do promienia. Euler po raz pierwszy użył $π$ = 3,14... w swojej pracy Mechanica z 1736 r. , a następnie kontynuował w swojej poczytnej pracy z 1748 r. Introductio in analysin infinitorum (pisał: „ze względu na zwięzłość zapiszemy tę liczbę jako $π$ ; stąd $π$ jest równe do połowy obwodu koła o promieniu 1”). Ponieważ Euler korespondował intensywnie z innymi matematykami w Europie, użycie greckiej litery szybko się rozprzestrzeniło, a praktyka ta została następnie powszechnie przyjęta w świecie zachodnim , chociaż definicja wciąż wahała się od 3,14... do 6,28... aż do 1761 r. .

Nowoczesne poszukiwanie większej liczby cyfr

Era komputerów i algorytmy iteracyjne

Oficjalne zdjęcie łysiejącego mężczyzny w garniturze

John von Neumann był członkiem zespołu, który jako pierwszy użył komputera cyfrowego ENIAC do obliczenia

π

.

Gaussa-Legendre'a iteracyjny algorytm :
Inicjalizacja

${\ Displaystyle \ scriptstyle a_ {0} = 1 \ quad b_ {0} = {\ Frac {1} {\ sqrt {2}}} \ quad t_ {0} = {\ Frac {1} {4} },\quad p_{0}=1.}$

Powtarzać

${\ Displaystyle \ scriptstyle a_ {n + 1} = {\ Frac {a_ {n} + b_ {n}} {2}}, \ quad \ quad b_ {n + 1} = {\ sqrt {a_ {n} b_{n}}},}$

${\ Displaystyle \ scriptstyle t_ {n + 1} = t_ {n}-p_ {n} (a_ {n}-a_ {n + 1}) ^ {2}, \ quad \ quad p_ {n + 1} = 2p_{n}.}$

Wtedy oszacowanie $π$ jest podane przez

${\ Displaystyle \ scriptstyle \ pi \ około {\ Frac {(a_ {n} + b_ {n}) ^ {2} {4t_ {n}}}.}$

Rozwój komputerów w połowie XX wieku ponownie zrewolucjonizował polowanie na cyfry $π$ . Matematycy John Wrench i Levi Smith osiągnęli 1120 cyfr w 1949 roku, używając kalkulatora biurkowego. Korzystając z nieskończonego szeregu odwrotnego tangensa (arctan), zespół kierowany przez George'a Reitwiesnera i Johna von Neumanna w tym samym roku osiągnął 2037 cyfr przy obliczeniach, które zajęły 70 godzin czasu pracy komputera na komputerze ENIAC . Rekord, zawsze oparty na serii arctan, był wielokrotnie łamany (7480 cyfr w 1957; 10 000 cyfr w 1958; 100 000 cyfr w 1961) aż do osiągnięcia 1 miliona cyfr w 1973 roku.

Dwa dodatkowe wydarzenia około 1980 roku po raz kolejny przyspieszyły zdolność do obliczania $π$ . Po pierwsze, odkrycie nowych algorytmów iteracyjnych do obliczania $π$ , które były znacznie szybsze niż nieskończone szeregi; a po drugie, wynalezienie algorytmów szybkiego mnożenia, które mogą bardzo szybko mnożyć duże liczby. Takie algorytmy są szczególnie ważne we współczesnych obliczeniach $π,$ ponieważ większość czasu komputera poświęca się na mnożenie. Obejmują one algorytm Karatsuby , mnożenie Toom-Cook i metody oparte na transformacji Fouriera .

Algorytmy iteracyjne zostały niezależnie opublikowane w latach 1975-1976 przez fizyka Eugene'a Salamina i naukowca Richarda Brenta . Unikają one polegania na nieskończonych seriach. Algorytm iteracyjny powtarza określone obliczenia, każda iteracja wykorzystuje dane wyjściowe z poprzednich kroków jako dane wejściowe i generuje wynik w każdym kroku, który jest zbieżny do pożądanej wartości. Podejście to zostało faktycznie wymyślone ponad 160 lat wcześniej przez Carla Friedricha Gaussa , w tym, co obecnie nazywa się metodą średniej arytmetyczno-geometrycznej (metoda AGM) lub algorytmem Gaussa-Legendre'a . Zmodyfikowany przez Salamina i Brenta, jest również określany jako algorytm Brenta-Salamina.

Algorytmy iteracyjne były szeroko stosowane po 1980 r., ponieważ są szybsze niż algorytmy nieskończonych szeregów: podczas gdy nieskończone szeregi zwykle zwiększają liczbę poprawnych cyfr w sposób addytywny w kolejnych terminach, algorytmy iteracyjne zazwyczaj mnożą liczbę poprawnych cyfr na każdym kroku. Na przykład algorytm Brenta-Salamina podwaja liczbę cyfr w każdej iteracji. W 1984 roku bracia John i Peter Borwein stworzyli algorytm iteracyjny, który czterokrotnie zwiększa liczbę cyfr w każdym kroku; aw 1987 r. zwiększa liczbę cyfr pięciokrotnie w każdym kroku. Metody iteracyjne zostały wykorzystane przez japońskiego matematyka Yasumasę Kanada do ustanowienia kilku rekordów w obliczeniach $π w$ latach 1995-2002. Ta szybka zbieżność ma swoją cenę: algorytmy iteracyjne wymagają znacznie więcej pamięci niż szeregi nieskończone.

Motywy obliczania $π$

Gdy matematycy odkryli nowe algorytmy i komputery stały się dostępne, liczba znanych cyfr dziesiętnych

π

dramatycznie wzrosła. Skala pionowa jest logarytmiczna .

W przypadku większości obliczeń numerycznych obejmujących $π$ kilka cyfr zapewnia wystarczającą precyzję. Według Jörga Arndta i Christopha Haenela trzydzieści dziewięć cyfr wystarcza do wykonania większości obliczeń kosmologicznych , ponieważ jest to dokładność niezbędna do obliczenia obwodu obserwowalnego wszechświata z dokładnością do jednego atomu. Uwzględniając dodatkowe cyfry potrzebne do skompensowania błędów zaokrągleń obliczeniowych , Arndt dochodzi do wniosku, że kilkaset cyfr wystarczyłoby do dowolnego zastosowania naukowego. Mimo to ludzie ciężko pracowali, aby obliczyć $π$ na tysiące i miliony cyfr. Ten wysiłek można częściowo przypisać ludzkiemu przymusowi bicia rekordów, a takie osiągnięcia z $π$ często $trafiają na$ pierwsze strony gazet na całym świecie. Mają też praktyczne korzyści, takie jak testowanie superkomputerów , testowanie algorytmów analizy numerycznej (w tym wysoce precyzyjnych algorytmów mnożenia ); oraz w samej matematyce, dostarczając dane do oceny losowości cyfr $π$ .

Szybko zbieżne szeregi

Srinivasa Ramanujan , pracując w odosobnieniu w Indiach, wyprodukował wiele innowacyjnych serii do obliczania

π

.

Nowoczesne kalkulatory $π$ nie wykorzystują wyłącznie algorytmów iteracyjnych. W latach 80. i 90. odkryto nowe nieskończone serie, które są tak szybkie jak algorytmy iteracyjne, ale są prostsze i zużywają mniej pamięci. Szybkie algorytmy iteracyjne oczekiwano w 1914 roku, kiedy indyjski matematyk Srinivasa Ramanujan opublikował dziesiątki innowacyjnych nowych formuł dla $π$ , wyróżniających się elegancją, matematyczną głębią i szybką konwergencją. Jednym z jego wzorów, opartych na równaniach modularnych , jest

{\ Displaystyle {\ Frac {1} {\ pi}} = {\ Frac {2 {\ sqrt {2}}} {9801}} \ suma _ {k = 0} ^ {\ infty} {\ Frac {( 4k)!(1103+26390k)}{k!^{4}\lewo(396^{4k}\prawo)}}.}

Ta seria zbiega się znacznie szybciej niż większość serii arctan, w tym formuła Machin. Bill Gosper jako pierwszy użył go do postępów w obliczaniu $π$ , ustanawiając rekord 17 milionów cyfr w 1985 roku. Wzory Ramanujana antycypowały nowoczesne algorytmy opracowane przez braci Borwein ( Jonathan i Peter ) oraz braci Chudnovsky . Wzór Chudnovsky opracowany w 1987 ma

{\ Displaystyle {\ Frac {1} {\ pi}} = {\ Frac {12} {640320 ^ {3/2}}} \ suma _ {k = 0} ^ {\ infty} {\ Frac {(6k )!(13591409+545140134k)}{(3k)!\,k!^{3}(-640320)^{3k}}}.}

Daje około 14 cyfr $π$ na termin i był używany do kilku rekordowych obliczeń $π$ , w tym pierwszego, który przekroczył 1 miliard (10 ⁹ ) cyfr w 1989 przez braci Chudnovsky, 10 bilionów (10 ¹³ ) cyfr w 2011 Alexander Yee i Shigeru Kondo, ponad 22 biliony cyfr w 2016 roku autorstwa Petera Trueba i 50 bilionów cyfr autorstwa Timothy Mullican w 2020 roku. Aby uzyskać podobne wzory, zobacz także serię Ramanujan-Sato .

W 2006 roku matematyk Simon Plouffe użył algorytmu relacji liczb całkowitych PSLQ do wygenerowania kilku nowych formuł na $π$ , zgodnych z następującym szablonem:

{\ Displaystyle \ pi ^ {k} = \ suma _ {n = 1} ^ {\ infty} {\ Frac {1} {n ^ {k}}} \ lewo ({\ Frac {a} {q ^ { n}-1}}+{\frac {b}{q^{2n}-1}}+{\frac {c}{q^{4n}-1}}\right),}

gdzie $q$ to $e π$ (stała Gelfonda), $k$ jest liczbą nieparzystą , a $a, b, c$ są pewnymi liczbami wymiernymi obliczonymi przez Plouffe'a.

Metody Monte Carlo

Igła Buffona . Igły a i b są upuszczane losowo.

Na ćwiartce kwadratu z wpisanym kołem umieszcza się losowe kropki.

Metody Monte Carlo , oparte na losowych próbach, mogą być użyte do przybliżenia

π

.

Metody Monte Carlo , które oceniają wyniki wielokrotnych prób losowych, mogą być użyte do stworzenia przybliżeń $π$ . Igła Buffona jest jedną z takich technik: jeśli igła o długości $ℓ$ zostanie upuszczona $n$ razy na powierzchnię, na której równoległe linie są narysowane $t$ jednostek od siebie, a jeśli $x$ tych czasów zatrzyma się przecinając linię ( $x$ > 0), to można przybliżyć $π$ na podstawie liczb:

{\ Displaystyle \ pi \ około {\ Frac {2n \ ell} {xt}}.}

Inną metodą Monte Carlo obliczania $π$ jest narysowanie koła wpisanego w kwadrat i losowe umieszczenie w nim kropek. Stosunek kropek wewnątrz okręgu do całkowitej liczby kropek będzie w przybliżeniu równy $π/4$ .

Pięć przypadkowych spacerów z 200 krokami. Średnia próbki

| W 200 |

wynosi

μ = 56/5

, a więc

2(200)μ -2 \approx 3,19

mieści się w zakresie

0,05

od

π

.

Innym sposobem obliczenia $π$ przy użyciu prawdopodobieństwa jest rozpoczęcie od losowego błądzenia , wygenerowanego przez ciąg (uczciwych) rzutów monetą: niezależne zmienne losowe $X k$ takie, że $X k \in {-1,1}$ z równym prawdopodobieństwem. Powiązane błądzenie losowe to

{\ Displaystyle W_ {n} = \ suma _ {k = 1} ^ {n} X_ {k}}

tak, że dla każdego $n$ , $W n$ jest wyciągane z przesuniętego i skalowanego rozkładu dwumianowego . Ponieważ $n$ zmienia się, $W n$ definiuje (dyskretny) proces stochastyczny . Wtedy $π$ można obliczyć ze wzoru

{\ Displaystyle \ pi = \ lim _ {n \ do \ infty} {\ Frac {2n} {E [| W_ {n} |] ^ {2}}}.}

Ta metoda Monte Carlo jest niezależna od jakiegokolwiek związku z okręgami i jest konsekwencją centralnego twierdzenia granicznego , omówionego poniżej .

Te metody Monte Carlo do aproksymacji $π$ są bardzo powolne w porównaniu z innymi metodami i nie dostarczają żadnych informacji na temat dokładnej liczby uzyskanych cyfr. Dlatego nigdy nie są używane do przybliżania $π,$ gdy pożądana jest prędkość lub dokładność.

Algorytmy czopowe

W 1995 roku odkryto dwa algorytmy, które otworzyły nowe możliwości badań nad $π$ . Nazywa się je algorytmami czopowymi, ponieważ, podobnie jak woda kapiąca z czopa , tworzą pojedyncze cyfry $π$ , które nie są ponownie wykorzystywane po obliczeniu. Jest to w przeciwieństwie do nieskończonych szeregów lub algorytmów iteracyjnych, które zachowują i wykorzystują wszystkie cyfry pośrednie, aż do uzyskania ostatecznego wyniku.

Matematycy Stan Wagon i Stanley Rabinowitz stworzyli prosty algorytm czopowy w 1995 roku. Jego szybkość jest porównywalna z algorytmami arctan, ale nie tak szybka jak algorytmy iteracyjne.

Inny algorytm czopowy, algorytm ekstrakcji cyfr BBP , został odkryty w 1995 roku przez Simona Plouffe'a:

{\ Displaystyle \ pi = \ suma _ {k = 0} ^ {\ infty} {\ Frac {1} {16 ^ {k}}} \ lewo ({\ Frac {4} {8k + 1}} - { \frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right).}

Ta formuła, w przeciwieństwie do innych wcześniej, może wytworzyć dowolną indywidualną cyfrę szesnastkową $π$ bez obliczania wszystkich poprzednich cyfr. Poszczególne cyfry binarne można wyodrębnić z pojedynczych cyfr szesnastkowych, a cyfry ósemkowe z jednej lub dwóch cyfr szesnastkowych. Odkryto odmiany tego algorytmu, ale nie znaleziono jeszcze algorytmu wyodrębniania cyfr, który szybko tworzy cyfry dziesiętne. Ważnym zastosowaniem algorytmów wyodrębniania cyfr jest walidacja nowych twierdzeń obliczeń rekordu $π$ : po zajęciu nowego rekordu wynik dziesiętny jest konwertowany na szesnastkowy, a następnie algorytm wyodrębniania cyfr jest używany do obliczenia kilku losowych cyfr szesnastkowych pod koniec; jeśli są zgodne, zapewnia to miarę pewności, że całe obliczenie jest poprawne.

W latach 1998-2000 projekt obliczeń rozproszonych PiHex wykorzystywał formułę Bellarda (modyfikację algorytmu BBP) do obliczenia biliardowego ( ^10-15 ) bitu $π$ , który okazał się być równy 0. We wrześniu 2010 r. Yahoo! pracownik wykorzystywane firmy Hadoop aplikację na tysiąc komputerów w ciągu 23 dni, aby obliczyć 256 bitów z $Õ$ na dwóch quadrillionth (2 × 10 ¹⁵ th) Bit, który okazuje się być zero.

Rola i charakterystyka w matematyce

Ponieważ $π$ jest blisko spokrewnione z kołem, występuje w wielu wzorach z dziedziny geometrii i trygonometrii, szczególnie tych dotyczących okręgów, kul czy elips. Inne gałęzie nauki, takie jak statystyka, fizyka, analiza Fouriera i teoria liczb, również zawierają $π$ w niektórych ważnych formułach.

Geometria i trygonometria

Pole koła jest równe

π

razy zacienionej powierzchni. Powierzchnia okręgu jednostkowego wynosi

π

.

$π$ pojawia się we wzorach dla obszarów i objętości kształtów geometrycznych opartych na okręgach, takich jak elipsy , kule , stożki i tori . Poniżej znajdują się niektóre z bardziej powszechnych formuł, w których występuje $π$ .

Obwód koła o promieniu $r$ wynosi $2π r$ .
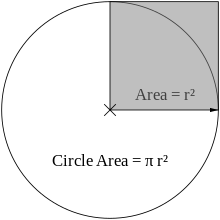
Pole okręgu o promieniu $r$ wynosi $π r 2$ .
Objętość kuli o promieniu $r$ wynosi $4 / 3 π r 3$ .
Pole powierzchni kuli o promieniu $r$ wynosi $4π r 2$ .

Powyższe wzory są szczególnymi przypadkami objętości n- wymiarowej kuli i pola powierzchni jej granicy, ( n −1)-wymiarowej kuli , podanej poniżej .

Pomiar szerokości trójkąta Reuleaux jako odległości między równoległymi liniami pomocniczymi . Ponieważ odległość ta nie zależy od kierunku linii, trójkąt Reuleaux jest krzywą o stałej szerokości.

Oprócz okręgów istnieją inne krzywe o stałej szerokości (orbiformy). Według twierdzenia Barbiera każda krzywa o stałej szerokości ma obwód $π$ razy jej szerokość. Reulaux trójkąt (utworzone przez przecięcie się trzech kół, z których każdy na środku, gdzie pozostałe dwa koła krzyżują) ma najmniejszy możliwy obszar, a jej szerokość koła największych. Istnieją również niekołowe gładkie krzywe o stałej szerokości.

Całki oznaczone, które opisują obwód, pole lub objętość kształtów generowanych przez okręgi, zazwyczaj mają wartości, które obejmują $π$ . Na przykład całka określająca połowę pola koła o promieniu jeden jest dana wzorem:

{\ Displaystyle \ int _ {-1} ^ {1} {\ sqrt {1-x ^ {2}}} \ dx = {\ Frac {\ pi} {2}}.}

W tej całce funkcja $\sqrt 1 - x 2$ reprezentuje górną połowę koła ( pierwiastek kwadratowy jest konsekwencją twierdzenia Pitagorasa ), a całka $\int 1 -1$ oblicza obszar między tą połową okręgu a osią $x$ .

Funkcje sinus i cosinus powtarzają się z okresem 2

π

.

Funkcje trygonometryczne opierają się na kątach, a matematycy zazwyczaj używają radianów jako jednostek miary. $π$ odgrywa ważną rolę w kątach mierzonych w radianach , które są zdefiniowane tak, że pełne koło obejmuje kąt 2 $π$ radianów. Miara kąta 180° jest równa $π$ radianom, a 1° = $π$ /180 radianów.

Wspólne funkcje trygonometryczne mają okresy będące wielokrotnościami $π$ ; na przykład, sinus i cosinus mają okres 2 $π$ , więc dla dowolnego kąta $θ$ i dowolnej liczby całkowitej $k$ ,

{\ Displaystyle \ sin \ theta = \ sin \ po lewej (\ theta +2 \ pi k \ prawej) {\ tekst {i}} \ cos \ theta = \ cos \ po lewej (\ theta +2 \ pi k \ po prawej) .}

Wartości własne

W harmoniczne wibracyjnej łańcuchowe są funkcje własne drugiej pochodnej i tworzą harmoniczny przebieg . Powiązane wartości własne tworzą ciąg arytmetyczny liczb całkowitych wielokrotności

π

.

Wiele wystąpień $π$ we wzorach matematyki i nauk ścisłych ma związek z jego bliskim związkiem z geometrią. Jednak $π$ pojawia się również w wielu naturalnych sytuacjach, które najwyraźniej nie mają nic wspólnego z geometrią.

W wielu zastosowaniach odgrywa znaczącą rolę jako wartość własna . Na przykład wyidealizowany wibrujący struna może być modelowany jako wykres funkcji $f$ na przedziale jednostkowym $[0,1]$ , ze stałymi końcami $f (0) = f (1) = 0$ . Tryby drgań struny są rozwiązaniami równania różniczkowego lub . Zatem $λ$ jest wartością własną drugiego operatora pochodnej i jest ograniczone przez teorię Sturma-Liouville'a do przyjmowania tylko pewnych określonych wartości. Musi być dodatnia, ponieważ operator jest ujemny , więc wygodnie jest napisać $λ = ν$ $2$ , gdzie $ν > 0$ nazywamy liczbą falową . Wtedy $f$ $($ $x$ $) = sin(π$ $x$ $)$ spełnia warunki brzegowe i równanie różniczkowe z $ν = π$ . ${\ Displaystyle f ''(x) + \ lambda f (x) = 0}$ ${\ Displaystyle f ''(t) = - \ lambda f (x)}$ $f\mapsto f''$

Wartość $π$ jest w rzeczywistości najmniejszą taką wartością liczby falowej i jest związana z podstawowym sposobem drgań struny. Jednym ze sposobów wykazania tego jest oszacowanie energii , która spełnia nierówność Wirtingera : dla funkcji ${\ Displaystyle \ mathbb {C}}$ gdzie $f (0) = f (1) = 0$ i $f$ , $f'$ oba są całkowalne do kwadratu , mamy :

{\ Displaystyle \ pi ^ {2} \ int _ {0} ^ {1} | f (x) | ^ {2} \ dx \ leq \ int _ {0} ^ {1} | f '(x) |^{2}\,dx,}

z równością dokładnie wtedy, gdy $f$ jest wielokrotnością $sin(π x)$ . Tutaj $π$ pojawia się jako optymalna stała w nierówności Wirtingera i wynika z tego, że jest to najmniejsza liczba falowa, wykorzystująca charakterystykę wariacyjną wartości własnej. W konsekwencji $π$ jest najmniejszą wartością osobliwą operatora pochodnego na przestrzeni funkcji na $[0,1]$ zanikających w obu punktach końcowych ( przestrzeń Sobolewa ). $H_{0}^{1}[0,1]$

Nierówności

Starożytnego miasta Kartaginy było rozwiązanie do isoperimetric problemu, według legendy, relacjonowanych przez Lorda Kelvina ( Thompson 1894 ): tych ziem położonych nad morzem, że Królowa Dydona mogła zamykania w na wszystkich innych stronach w obrębie jednej danej oxhide, pokroić w paski.

Liczba $π$ służy w podobnych problemach z wartościami własnymi w analizie wysokowymiarowej. Jak wspomniano powyżej , można ją scharakteryzować poprzez swoją rolę najlepszej stałej w nierówności izoperymetrycznej : obszar $A$ zamknięty przez płaszczyznę krzywa Jordana obwodu $P$ spełnia nierówność

{\ Displaystyle 4 \ pi A \ leq P ^ {2},}

a równość jest wyraźnie osiągnięta dla koła, ponieważ w tym przypadku $A = π r 2$ i $P = 2π r$ .

Ostatecznie, jako konsekwencja nierówności izoperymetrycznej, $π$ pojawia się w optymalnej stałej krytycznej nierówności Sobolewa w n wymiarach, co tym samym charakteryzuje rolę $π również$ w wielu zjawiskach fizycznych, na przykład w klasycznej teorii potencjału . W dwóch wymiarach krytyczna nierówność Sobolewa to:

{\ Displaystyle 2 \ pi \ | f \ | _ {2} \ leq \ | \ nabla f \ | _ {1}}

dla C gładkiej funkcji o zwartym nośniku w $R 2$ , jest nachylenie o f i i odnoszą się odpowiednio do $L$ $2$ i $L$ $1$ -norm . Nierówność Sobolewa jest równoważna nierówności izoperimetrycznej (w dowolnym wymiarze), z tymi samymi najlepszymi stałymi. ${\ Displaystyle \ nabla f}$ $\|f\|_{2}$ $\|\nabla f\|_{1}$

Nierówność Wirtinger za uogólnia również do wyższych wymiarów nierówności Poincaré , które zapewniają najlepsze stałe dla energii Dirichleta od An n błony wymiarowej. W szczególności $π$ jest największą stałą taką, że

{\ Displaystyle \ pi \ leq {\ Frac {\ lewo (\ int _ {G} | \ nabla u | ^ {2} \ po prawej) ^ {1/2} {\ po lewej (\ int _ {G} | u|^{2}\right)^{1/2}}}}

dla wszystkich podzbiorów wypukłych $G$ z $R n$ o średnicy 1 i funkcji całkowalnych z kwadratem u na $G$ o średniej zerowej. Tak jak nierówność Wirtingera jest wariacyjną formą problemu wartości własnej Dirichleta w jednym wymiarze, nierówność Poincarégo jest wariacyjną formą problemu wartości własnej Neumanna w dowolnym wymiarze.

Transformata Fouriera i zasada nieoznaczoności Heisenberga

Animacja geodezji w grupie Heisenberga , ukazująca ścisły związek między grupą Heisenberga, izoperymetrią i stałą

π

. Skumulowana wysokość geodezji jest równa powierzchni zacienionej części okręgu jednostkowego, podczas gdy długość łuku (w metryce Carnota-Carathéodory'ego ) jest równa obwodowi.

Stała $π$ pojawia się również jako krytyczny parametr widmowy w transformacji Fouriera . Jest to transformata całkowa , która bierze całkowalną funkcję o wartościach zespolonych $f$ na linii rzeczywistej do funkcji zdefiniowanej jako:

{\ Displaystyle {\ kapelusz {f}} (\ xi ) = \ int _ {- \ infty} ^ {\ infty} f (x) e ^ {-2 \ pi ix \ xi} \ dx.}

Chociaż istnieje kilka różnych konwencji transformaty Fouriera i jej odwrotności, każda taka konwencja musi zawierać gdzieś $π$ . Powyższe jest najbardziej kanoniczną definicją, jednak dającą unikalny operator unitarny na $L$ $2 ,$ który jest również homomorfizmem algebry $L$ $1$ do $L$ $\infty$ .

Zasada nieoznaczoności Heisenberga zawiera również numer $gatunku$ . Zasada nieoznaczoności daje ostrą dolną granicę stopnia, w jakim możliwe jest zlokalizowanie funkcji zarówno w przestrzeni, jak i częstotliwości: z naszymi konwencjami dla transformaty Fouriera,

{\ Displaystyle \ lewo (\ inft _ {- \ infty} ^ {\ infty} x ^ {2} | f (x) | ^ {2} \ dx \ po prawej) \ po lewej (\ inft _ {- \ infty }^{\infty }\xi ^{2}|{\hat {f}}(\xi )|^{2}\,d\xi \right)\geq \left({\frac {1}{4 \pi }}\int _{-\infty }^{\infty }|f(x)|^{2}\,dx\right)^{2}.}

Fizyczne konsekwencje niepewności w jednoczesnych obserwacjach położenia i pędu układu mechaniki kwantowej omówiono poniżej . Pojawienie $Õ$ we wzorach analizy Fouriera jest ostatecznie konsekwencją twierdzenia Kamień-von Neumanna , twierdząc wyjątkowość reprezentacji Schrödingera z grupy Heisenberga .

Całki Gaussa

Wykres funkcji Gaussa

ƒ (x) = e - x 2

. Kolorowy obszar pomiędzy funkcją a osią x ma obszar

\sqrt π

.

Pola prawdopodobieństwa i statystyki często wykorzystują rozkład normalny jako prosty model dla złożonych zjawisk; na przykład naukowcy ogólnie zakładają, że błąd obserwacji w większości eksperymentów ma rozkład normalny. Funkcja Gaussa , która jest funkcją gęstości prawdopodobieństwa rozkładu normalnego ze średnią $μ$ i odchyleniem standardowym $σ$ , zawiera naturalnie $π$ :

{\ Displaystyle f (x) = {1 \ nad \ sigma {\ sqrt {2 \ pi}}} \ e ^ {- (x- \ mu) ^ {2} / (2 \ sigma ^ {2}) }.}

Współczynnik o powoduje, że obszar pod wykresem $f jest$ równy jeden, co jest wymagane dla rozkładu prawdopodobieństwa. Wynika to ze zmiany zmiennych w całce Gaussa : ${\tfrac {1}{\sqrt {2\pi}}}$

{\ Displaystyle \ int _ {- \ infty} ^ {\ infty} e ^ {-u ^ {2}} \ du = {\ sqrt {\ pi}}}

co mówi, że obszar pod podstawową krzywą dzwonową na rysunku jest równy pierwiastkowi kwadratowemu z $π$ .

π

można obliczyć z rozkładu zer jednowymiarowego procesu Wienera

Centralne twierdzenie graniczne wyjaśnia centralną rolę rozkładów normalnych, a tym samym $Õ$ , prawdopodobieństwa i statystyki. Twierdzenie to jest ostatecznie związany z spektralnej charakteryzacji z $Õ$ jako wartości własnej związanej z zasadą nieoznaczoności Heisenberga, oraz fakt, że równość w zasadzie nieoznaczoności tylko dla funkcji Gaussa. Równoważnie, $π$ jest unikalną stałą, która powoduje, że rozkład normalny Gaussa $e -π x 2 jest$ równy jego własnej transformacji Fouriera. Rzeczywiście, według Howe'a (1980) , „cała sprawa” ustanowienia podstawowych twierdzeń analizy Fouriera sprowadza się do całki Gaussa.

Geometria rzutowa

Niech $V$ będzie zbiorem wszystkich podwójnie różniczkowalnych funkcji rzeczywistych spełniających równanie różniczkowe zwyczajne . Wtedy $V$ jest dwuwymiarową rzeczywistą przestrzenią wektorów , z dwoma parametrami odpowiadającymi parze warunków początkowych równania różniczkowego. Dla any niech będzie funkcjonał oceny, który przyporządkuje każdemu wartość funkcji $f$ w rzeczywistym punkcie $t$ . Następnie, dla każdego t The ziaren od jest jednowymiarowym liniowym podprzestrzeń $V$ . Stąd określa funkcję od linii rzeczywistej do rzeczywistej linii rzutowej . Funkcja ta jest okresowa, a wielkość $π$ można scharakteryzować jako okres tego odwzorowania. ${\ Displaystyle f: \ mathbb {R} \ do \ mathbb {R}}$ ${\ Displaystyle f''(x)+f(x)=0}$ ${\ Displaystyle t \ w \ mathbb {R} }$ ${\ Displaystyle e_ {t}: V \ do \ mathbb {R}}$ ${\ Displaystyle f \ w V}$ ${\ Displaystyle e_ {t} (f) = f (t)}$ $e_{t}$ ${\ Displaystyle t \ mapsto \ ker e_ {t}}$ ${\ Displaystyle \ mathbb {R} \ do \ mathbb {P} (V)}$

Topologia

Uniformizacji z Quartic Klein , powierzchnia rodzaju trzy i charakterystyki Eulera -4, a iloraz hiperbolicznej płaszczyźnie przez grupa symetrii PSL (2,7) na płaszczyźnie Fano . Obszar hiperboliczny domeny podstawowej to

8π

, według Gaussa-Bonneta.

Stała $π$ pojawia się we wzorze Gaussa-Bonneta, który odnosi różniczkową geometrię powierzchni do ich topologii . W szczególności, jeśli zwarta powierzchnia $Σ$ ma krzywiznę Gaussa K , to

{\ Displaystyle \ int _ {\ Sigma} K \, dA = 2 \ pi \ chi (\ Sigma)}

gdzie $χ (Σ)$ jest cechą Eulera , która jest liczbą całkowitą. Przykładem jest pole powierzchni kuli S o krzywiźnie 1 (tak, że jej promień krzywizny , który pokrywa się z jej promieniem, również wynosi 1.). Cechę Eulera kuli można obliczyć z jej grup homologii i okazuje się, że równa się dwóm. Tak więc mamy

{\ Displaystyle A (S) = \ int _ {S} 1 \ dA = 2 \ pi \ cdot 2 = 4 \ pi}

odwzorowując wzór na pole powierzchni kuli o promieniu 1.

Stała pojawia się w wielu innych formułach całkowych w topologii, w szczególności tych obejmujących charakterystyczne klasy poprzez homomorfizm Cherna-Weila .

Rachunek wektorowy

Techniki rachunku wektorowego można rozumieć w kategoriach dekompozycji na harmoniki sferyczne (pokazano)

Rachunek wektorowy jest gałęzią rachunku różniczkowego, która zajmuje się właściwościami pól wektorowych i ma wiele zastosowań fizycznych, takich jak elektryczność i magnetyzm . Newtona potencjał dla punktowego źródła $Q$ usytuowanego u źródła trójwymiarowego układu współrzędnych kartezjańskich

{\ Displaystyle V (\ mathbf {x} ) = - {\ Frac {kQ} {| \ mathbf {x} |}}}

która reprezentuje energię potencjalną jednostki masy (lub ładunku) umieszczonej w odległości $| x |$ od źródła, a $k$ jest stałą wymiarową. Pole, oznaczane tutaj przez $E$ , które może być (newtonowskim) polem grawitacyjnym lub (kulombowskim) polem elektrycznym , jest ujemnym gradientem potencjału:

{\ Displaystyle \ mathbf {E} = - \ Nabla V.}

Przypadki specjalne obejmują prawo Coulomba i prawo powszechnego ciążenia Newtona . Prawo Gaussa mówi, że zewnętrzny strumień pola przez dowolną gładką, prostą, zamkniętą, orientowalną powierzchnię $S$ zawierającą początek jest równy $4 π kQ$ :

{\ Displaystyle 4 \ pi kQ =}

$\oiint$

{\scriptstyle S}

{\ Displaystyle \ mathbf {E} \ cdot d \ mathbf {A}.}

Standardem jest wchłonięcie tego współczynnika $4π$ do stałej $k$ , ale ten argument pokazuje , dlaczego musi on gdzieś się pojawić . Ponadto $4π$ to pole powierzchni sfery jednostkowej, ale nie założyliśmy, że $S$ jest sferą. Jednak w konsekwencji twierdzenia o dywergencji , ponieważ obszar oddalony od początku jest próżnią (bez źródła), tylko klasa homologii powierzchni $S$ w $R 3 \{0} ma$ znaczenie przy obliczaniu całki, więc można zastąpić dowolną dogodną powierzchnią w tej samej klasie homologii, w szczególności sferą, w której do obliczenia całki można wykorzystać współrzędne sferyczne.

Konsekwencją prawa Gaussa jest to, że ujemny Laplace'a potencjału $V$ jest równy $4π kQ$ razy delta Diraca :

{\ Displaystyle \ Delta V (\ mathbf {x} ) = -4 \ pi kQ \ delta (\ mathbf {x}).}

Bardziej ogólne rozkłady materii (lub ładunku) uzyskuje się z tego przez splot , dając równanie Poissona

{\ Displaystyle \ Delta V (\ mathbf {x} ) = -4 \ pi k \ rho (\ mathbf {x})}

gdzie $ρ$ jest funkcją dystrybucji.

Równanie Einsteina mówi, że krzywizna czasoprzestrzeni jest spowodowana zawartością materii i energii.

Stała $π$ odgrywa analogiczną rolę potencjałów czterowymiarowych związanych z równań Einsteina , podstawowej formuły, która stanowi podstawę do ogólnej teorii względność i opisuje oddziaływania podstawowe z grawitacji , w wyniku czasoprzestrzeni jest zakrzywiona od materii i energii :

{\ Displaystyle R_ {\ mu \ nu} - {\ Frac {1} {2}} Rg_ {\ mu \ nu} + \ Lambda g_ {\ mu \ nu} = {\ Frac {8 \ pi G} {c ^{4}}}T_{\mu \nu },}

gdzie $R μν$ to tensor krzywizny Ricciego , $R$ to krzywizna skalarna , $g μν$ to tensor metryczny , $Λ$ to stała kosmologiczna , $G$ to stała grawitacyjna Newtona , $c$ to prędkość światła w próżni, a $T μν$ to naprężenie– tensor energii . Lewa strona równania Einsteina jest nieliniowym odpowiednikiem Laplace'a tensora metrycznego i sprowadza się do granicy słabego pola, gdzie termin pełni rolę mnożnika Lagrange'a , a prawa strona jest analog funkcji dystrybucji, razy $8π$ . ${\ Displaystyle \ Lambda g}$

Całka Cauchy'ego

Złożone funkcje analityczne można wizualizować jako zbiór linii prądu i ekwipotencjałów, czyli układy krzywych przecinających się pod kątem prostym. Tutaj zilustrowany jest złożony logarytm funkcji Gamma.

Jednym z kluczowych narzędzi w analizie złożonej jest całkowanie konturowe funkcji na dodatnio zorientowanej ( prostowalnej ) krzywej Jordana $γ$ . Forma całki Cauchy'ego mówi, że jeśli punkt $z 0$ jest wewnątrz $γ$ , to

{\ Displaystyle \ oint _ {\ gamma} {\ Frac {dz} {z-z_ {0}}} = 2 \ pi ja.}

Chociaż krzywa $γ$ nie jest kołem, a więc nie ma żadnego oczywistego związku ze stałą $π$ , standardowy dowód tego wyniku wykorzystuje twierdzenie Morery , z którego wynika, że całka jest niezmienna w homotopii krzywej, tak że może być zdeformowany do okręgu, a następnie wyraźnie zintegrowany we współrzędnych biegunowych. Mówiąc ogólniej, prawdą jest, że jeśli prostowalna krzywa zamknięta $γ$ nie zawiera $z 0$ , to powyższa całka jest $2π i$ razy liczba uzwojeń krzywej.

Ogólna postać integralnego wzorze Cauchy'ego ustanawia zależność między wartościami złożonego analitycznej funkcji $f (oo)$ na krzywej Jordan $y$ a wartość $f (Z),$ w dowolnym punkcie wewnętrznym $Z 0$ o $y$ :

{\ Displaystyle \ oint _ {\ gamma} {f (z) \ nad z-z_ {0}} \ dz = 2 \ pi jeśli (z_ {0})}

pod warunkiem, że $f (z)$ jest analityczne w obszarze zamkniętym przez $γ$ i rozciąga się w sposób ciągły do $γ$ . Całkowa formuła Cauchy'ego jest szczególnym przypadkiem twierdzenia o resztach , że jeśli $g (z)$ jest funkcją meromorficzną obszar otoczony przez $γ$ i jest ciągły w sąsiedztwie $γ$ , to

{\ Displaystyle \ oint _ {\ gamma} g (z) \ dz = 2 \ pi ja \ suma \ operatorname {Res} (g, a_ {k})}

gdzie suma z reszt w tych biegunów o $g (oo)$ .

Funkcja gamma i przybliżenie Stirlinga

Hopf fibration z 3-kuli przez koła Villarceau , na złożonym rzutowej zgodnie z jego metryka Fubiniego-Study (przedstawiono trzy Podobieństwa). Konsekwencją jest tożsamość

S 3 (1)/ S 2 (1) = π/2

.

Funkcja silni $n!$ jest iloczynem wszystkich dodatnich liczb całkowitych przez $n$ . Funkcja gamma rozszerza pojęcie silni (zwykle definiowanej tylko dla nieujemnych liczb całkowitych) na wszystkie liczby zespolone, z wyjątkiem ujemnych liczb całkowitych. Gdy funkcja gamma jest obliczana na liczbach połówkowych, wynik zawiera $π$ ; na przykład i . ${\ Displaystyle \ Gamma (1/2) = {\ sqrt {\ pi}}}$ ${\textstyle \Gamma (5/2)={\frac {3{\sqrt {\pi }}}{4}}}$

Funkcja gamma jest zdefiniowana przez rozwój produktu Weierstrass :

{\ Displaystyle \ Gamma (z) = {\ Frac {e ^ {-\ gamma z}} {z}} \ prod _ {n = 1} ^ {\ infty} {\ Frac {e ^ {z / n} }{1+z/n}}}

gdzie $γ$ jest stałą Eulera-Mascheroni . Obliczone przy $z = 1/2$ i podniesione do kwadratu, równanie $Γ(1/2) 2 = π$ redukuje się do wzoru iloczynu Wallisa. Funkcja gamma jest również powiązana z funkcją zeta Riemanna i tożsamościami wyznacznika funkcjonalnego , w którym ważną rolę odgrywa stała $π$ .

Funkcja y jest wykorzystywana do obliczenia objętości $V n (R)$ w n -wymiarowej kuli o promieniu R w euklidesowej n -wymiarowej przestrzeni i powierzchnia $S n -1 (R)$ na jego brzegu, ( n -1 )-wymiarowa kula :

{\ Displaystyle V_ {n} (r) = {\ Frac {\ pi ^ {n/2}} {\ Gamma \ lewo ({\ Frac {n} {2}} + 1 \ po prawej)}} R ^ { n},}

{\ Displaystyle S_ {n-1} (r) = {\ Frac {n \ pi ^ {n/2}} {\ Gamma \ lewo ({\ Frac {n} {2}} + 1 \ prawej)}} r^{n-1}.}

Ponadto z równania funkcyjnego wynika, że

{\ Displaystyle 2 \ pi r = {\ Frac {S_ {n + 1} (r)} {V_ {n} (r)}}.}

Funkcja gamma może być użyta do stworzenia prostego przybliżenia do funkcji silni $n!$ dla dużego $n$ : co jest znane jako przybliżenie Stirlinga . Równoważnie, ${\textstyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}}$

{\ Displaystyle \ pi = \ lim _ {n \ do \ infty} {\ Frac {e ^ {2 n} n! ^ {2}} {2 n ^ {2 n + 1}}}.}

Jako geometryczne zastosowanie przybliżenia Stirlinga, niech $Δ n$ oznacza standardowy simpleks w n- wymiarowej przestrzeni euklidesowej, a $(n + 1)Δ n$ oznacza simpleks, którego wszystkie boki są powiększone o współczynnik $n + 1$ . Następnie

{\ Displaystyle \ Operatorname {Vol} ((n + 1) \ Delta _ {n}) = {\ Frac {(n + 1) ^ {n}} {n!}} \ SIM {\ Frac {e ^ { n+1}}{\sqrt {2\pi n}}}.}

Hipoteza Ehrharta dotycząca objętości jest taka, że jest to (optymalna) górna granica objętości ciała wypukłego zawierającego tylko jeden punkt sieci .

Teoria liczb i funkcja zeta Riemanna

Każda liczba pierwsza ma powiązaną grupę Prüfera , które są arytmetycznymi lokalizacjami koła. Do L-funkcje analitycznej teorii numer zlokalizowane są w każdym głównego p .

Rozwiązanie problemu bazylejskiego z wykorzystaniem hipotezy Weila : wartość

ζ (2)

jest hiperbolicznym obszarem fundamentalnej dziedziny grupy modułowej , razy

π /2

.

Funkcja zeta Riemanna $ζ (s)$ jest używana w wielu dziedzinach matematyki. Przy ocenie przy $s = 2$ można to zapisać jako

{\ Displaystyle \ zeta (2) = {\ Frac {1} {1 ^ {2}}} + {\ Frac {1} {2 ^ {2}}} + {\ Frac {1} {3 ^ {2} }}}+\cdots }

Znalezienie prostego rozwiązania dla tego nieskończonego szeregu było słynnym problemem matematycznym zwanym problemem bazylejskiego . Leonhard Euler rozwiązał go w 1735 r., kiedy wykazał, że jest ono równe $π 2 /6$ . Wynik Eulera prowadzi do wniosku z teorii liczb, że prawdopodobieństwo, że dwie liczby losowe będą względnie pierwsze (to znaczy nie będą miały wspólnych czynników) jest równe $6/π 2$ . Prawdopodobieństwo to opiera się na obserwacji, że prawdopodobieństwo, że dowolna liczba jest podzielna przez liczbę pierwszą $p$ wynosi $1/ p$ (na przykład każda 7 liczba całkowita jest podzielna przez 7.) Stąd prawdopodobieństwo, że obie liczby są podzielne przez tę liczbę pierwszą wynosi $1 / p 2$ , a prawdopodobieństwo, że przynajmniej jeden z nich nie jest, wynosi $1 - 1/ p 2$ . Dla różnych liczb pierwszych te zdarzenia podzielności są od siebie niezależne; więc prawdopodobieństwo, że dwie liczby są względnie pierwsze, jest podane przez iloczyn wszystkich liczb pierwszych:

{\ Displaystyle {\ zacząć {wyrównany} \ prod _ {p} ^ {\ infty} \ lewo (1-{\ Frac {1} {p ^ {2}}} \ po prawej) = \ po lewej (\ prod _ {p}^{\infty }{\frac {1}{1-p^{-2}}}\right)^{-1}\\[4pt]&={\frac {1}{1+{ \frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots }}\\[4pt]&={\frac {1}{\zeta ( 2)}}={\frac {6}{\pi ^{2}}}\ok 61\%.\end{wyrównane}}}

Prawdopodobieństwo to można wykorzystać w połączeniu z generatorem liczb losowych do przybliżenia $π$ przy użyciu podejścia Monte Carlo.

Z rozwiązania problemu bazylejskiego wynika, że geometrycznie wyprowadzona wielkość $π$ jest głęboko związana z rozkładem liczb pierwszych. Jest to szczególny przypadek hipotezy Weila o liczbach Tamagawy , która zapewnia równość podobnych takich nieskończonych iloczynów wielkości arytmetycznych , zlokalizowanych przy każdej liczbie pierwszej p , i wielkości geometrycznej : odwrotności objętości pewnej lokalnie symetrycznej przestrzeni . W przypadku problemu Basel, to hiperboliczny 3-kolektor $SL 2 (R) / SL 2 (Z)$ .

Funkcja zeta spełnia również równanie funkcyjne Riemanna, które obejmuje $π$ oraz funkcję gamma:

{\ Displaystyle \ zeta (s) = 2 ^ {s} \ pi ^ {s-1} \ \ sin \ lewo ({\ Frac {\ pi s} {2}} \ po prawej) \ \ Gamma (1-s )\ \zeta (1-s).}

Ponadto pochodna funkcji zeta spełnia

{\ Displaystyle \ exp (- \ zeta '(0)) = {\ sqrt {2 \ pi}}.}

Konsekwencją jest to, że $π$ można otrzymać z funkcjonalną determinantę z oscylatora harmonicznego . Ten wyznacznik funkcjonalny można obliczyć poprzez rozwinięcie iloczynu i jest on równoważny ze wzorem iloczynu Wallisa. Obliczenia można przetworzyć w mechanice kwantowej , a konkretnie w wariacyjnym podejściu do widma atomu wodoru .

Szeregi Fouriera

π

pojawia się w znakach liczb p-adycznych (pokazanych), które są elementami grupy Prüfera . Teza Tate'a intensywnie wykorzystuje tę maszynerię.

Stała $π$ występuje również naturalnie w szeregu Fouriera z funkcji okresowych . Funkcje okresowe to funkcje na grupie $T = R / Z$ części ułamkowych liczb rzeczywistych. Fouriera wskazuje rozkładu że funkcja zespolona $C$ na $T$ może być zapisany jako nieskończona liniowego nakładania jednostkowych postaci o $T$ . To znaczy homomorfizmy grup ciągłych od $T$ do grupy kołowej $U (1)$ liczb zespolonych modułowych. Jest to twierdzenie, że każdy znak $T$ jest jednym ze złożonych wykładników . ${\ Displaystyle e_ {n} (x) = e ^ {2 \ pi inx}}$

Istnieje unikalny charakter na $T$ , aż do złożonej koniugacji, czyli izomorfizmu grupowego. Stosując miarę Haara na grupie kołowej, stała $π$ jest połową wielkości pochodnej Radona-Nikodyma tego znaku. Pozostałe znaki mają pochodne, których wielkości są dodatnimi całkowitymi wielokrotnościami 2 $π$ . W rezultacie stała $π$ jest unikatową liczbą taką, że grupa T , wyposażona w miarę Haara, jest dwoistością Pontrjagin do sieci całkowitych wielokrotności 2 $π$ . Jest to wersja jednowymiarowej formuły sumowania Poissona .

Formy modułowe i funkcje theta

Funkcje Theta przekształcają się pod siatką okresów krzywej eliptycznej.

Stała $π$ związana jest głęboko z teorią form modularnych i funkcji theta . Na przykład, algorytm Chudnovsky wiąże się w istotny sposób do Niezmiennik J danego krzywej eliptycznej .

Formy modularne to funkcje holomorficzne w górnej połowie płaszczyzny charakteryzujące się ich właściwościami przekształcenia pod grupę modularną (lub jej różne podgrupy), sieć w grupie . Przykładem jest funkcja Jacobi theta ${\ Displaystyle \ operatorname {SL} _ {2} (\ mathbb {Z})}$ ${\ Displaystyle \ operatorname {SL} _ {2} (\ mathbb {R})}$

{\ Displaystyle \ theta (z \ tau) = \ suma _ {n = - \ infty} ^ {\ infty} e ^ {2 \ pi inz + i \ pi n ^ {2} \ tau}}

który jest rodzajem formy modułowej zwanej formą Jacobiego . Czasami jest to pisane w formie nome . $q=e^{\pi ja\tau}$

Stała $π$ jest unikalną stałą , która sprawia, że funkcja theta Jacobiego ma postać automorficzną , co oznacza, że przekształca się w określony sposób. Pewne tożsamości obowiązują dla wszystkich form automorficznych. Przykładem jest

{\ Displaystyle \ theta (z + \ tau \ tau ) = e ^ {- \ pi ja \ tau -2 \ pi iz} \ theta (z \ tau)}

co oznacza, że $θ$ przekształca się jako reprezentacja w ramach dyskretnej grupy Heisenberga . Ogólne formy modularne i inne funkcje teta również obejmują $π$ , ponownie z powodu twierdzenia Stone-von Neumann .

Rozkład Cauchy'ego i teoria potencjału

Lok Agnesi , nazwana Maria Agnesi (1718-1799), to konstrukcji geometrycznej wykresu rozkładu Cauchy'ego.

Rozkład Cauchyego

{\ Displaystyle g (x) = {\ Frac {1} {\ pi}} \ cdot {\ Frac {1} {x ^ {2} + 1}}}

jest funkcją gęstości prawdopodobieństwa . Całkowite prawdopodobieństwo jest równe jeden dzięki całce:

{\ Displaystyle \ int _ {- \ infty} ^ {\ infty} {\ Frac {1} {x ^ {2} + 1}} \ dx = \ pi.}

Shannon entropia rozkładu Cauchy'ego wynosi $ln (4π)$ , który obejmuje również $π$ .

Rozkład Cauchy'ego reguluje przechodzenie cząstek Browna przez błonę.

Rozkład Cauchy'ego odgrywa ważną rolę w teorii potencjału, ponieważ jest to najprostsza miara Furstenberga , klasyczne jądro Poissona związane z ruchem Browna w półpłaszczyźnie. Sprzężone funkcje harmoniczne, a więc także transformata Hilberta, są związane z asymptotykami jądra Poissona. Transformaty Hilberta H jest integralną transformacji podana przez Cauchy'ego Nadrzędną wartością w pojedynczej całki

{\ Displaystyle Hf (t) = {\ Frac {1} {\ pi}} \ int _ {- \ infty} ^ {\ infty} {\ Frac {f (x) \, dx} {xt}}.}

Stała $π$ jest unikalnym (dodatnim) czynnikiem normalizującym, takim, że H definiuje liniową strukturę złożoną w przestrzeni Hilberta całkowalnych do kwadratu funkcji o wartościach rzeczywistych na prostej. Transformata Hilberta, podobnie jak transformata Fouriera, może być scharakteryzowana wyłącznie w kategoriach jej właściwości transformacji w przestrzeni Hilberta $L 2 (R)$ : aż do współczynnika normalizacji jest to unikalny ograniczony operator liniowy, który komutuje z dodatnimi dylatacjami i anty- dojeżdża ze wszystkimi odbiciami rzeczywistej linii. Stała $π$ jest unikalnym czynnikiem normalizującym, który czyni tę transformację jednostkową.

Złożona dynamika

π

można obliczyć ze zbioru Mandelbrota , licząc liczbę iteracji wymaganych przed rozbieżnością punktu

(-0.75, ε)

.

Zdarzenie z $Õ$ w zbiorze Mandelbrota fraktala została odkryta przez Davida Boll w 1991 roku badał zachowanie zbioru Mandelbrota w pobliżu „na karku” $(-0.75, 0)$ . Jeśli brane są pod uwagę punkty o współrzędnych $(-0.75, ε)$ , ponieważ $ε$ dąży do zera, liczba iteracji aż do rozbieżności dla punktu pomnożona przez $ε$ zbiega się do $π$ . Podobnie zachowuje się punkt $(0,25 + ε, 0)$ na wierzchołku dużej „doliny” po prawej stronie zbioru Mandelbrota: liczba iteracji aż do dywergencji pomnożona przez pierwiastek kwadratowy z $ε$ dąży do $π$ .

Matematyka poza matematyką

Opisywanie zjawisk fizycznych

Chociaż nie jest stałą fizyczną , $π$ pojawia się rutynowo w równaniach opisujących podstawowe zasady wszechświata, często ze względu na stosunek $π$ do okręgu i sferycznych układów współrzędnych . Prosty wzór z dziedziny mechaniki klasycznej podaje przybliżony okres $T$ wahadła prostego o długości $L$ , kołyszącego się z niewielką amplitudą ( $g$ jest przyspieszeniem ziemskim ):

{\ Displaystyle T \ około 2 \ pi {\ sqrt {\ Frac {L} {g}}}.}

Jednym z kluczowych wzorów mechaniki kwantowej jest zasada nieoznaczoności Heisenberga , która pokazuje, że niepewność pomiaru położenia cząstki (Δ $x$ ) i pędu (Δ $p$ ) nie może być jednocześnie arbitralnie mała (gdzie $h$ jest stałą Plancka ):

{\ Displaystyle \ Delta x \ \ Delta p \ geq {\ Frac {h} {4 \ pi}}.}

Fakt, że $π$ jest w przybliżeniu równe 3, odgrywa rolę w stosunkowo długim okresie życia ortopozytronium . Odwrotny czas życia do najniższego rzędu w stałej struktury subtelnej $α$ wynosi

{\ Displaystyle {\ Frac {1} {\ tau}} = 2 {\ Frac {\ pi ^ {2}-9} {9 \ pi}} m \ alfa ^ {6}}

gdzie $m$ jest masą elektronu.

$π$ występuje w niektórych wzorach inżynierii budowlanej, takich jak wzór na wyboczenie wyprowadzony przez Eulera, który podaje maksymalne obciążenie osiowe $F,$ jakie długi, smukły słup o długości $L$ , module sprężystości $E$ , i powierzchniowym momencie bezwładności $I$ może przenieść bez wyboczenia :

{\ Displaystyle F = {\ Frac {\ pi ^ {2} EI} {L ^ {2}}}.}

Pole dynamiki płynów zawiera $π$ w prawie Stokesa , które przybliża siłę tarcia $F$ wywieraną na małe, kuliste obiekty o promieniu $R$ , poruszające się z prędkością $v$ w płynie o lepkości dynamicznej $η$ :

{\ Displaystyle F = 6 \ pi \ eta Rv.}

W elektromagnetyce stała przepuszczalności próżni μ ₀ występuje w równaniach Maxwella , które opisują właściwości pól elektrycznych i magnetycznych oraz promieniowania elektromagnetycznego . Przed 20 maja 2019 r. był określany jako dokładnie

{\ Displaystyle \ mu _ {0}= 4 \ pi \ razy 10 ^ {-7} \ tekst { H / m}} \ około 1.2566370614 \ ldots \ razy 10 ^ {-6} {\ tekst { nie dotyczy }}^{2}.}

Zależność prędkości światła w próżni $c$ można wyprowadzić z równań Maxwella w ośrodku klasycznej próżni, wykorzystując zależność między μ ₀ a stałą elektryczną (przenikalność próżniową) , $ε 0$ w jednostkach SI:

{\ Displaystyle c = {1 \ ponad {\ sqrt {\ mu _ {0} \ varepsilon _ {0}}}}.}

W idealnych warunkach (jednolity łagodnym zboczu na jednorodnie erodującego podłoża), to zakręt o meandrującej rzeki zbliża $gatunku$ . Falistość to stosunek między rzeczywistą długością a odległością w linii prostej od źródła do ujścia. Szybsze prądy wzdłuż zewnętrznych krawędzi zakoli rzeki powodują większą erozję niż wzdłuż krawędzi wewnętrznych, tym samym wypychając zakola jeszcze dalej i zwiększając ogólną pętlę rzeki. Jednak, że loopiness ostatecznie powoduje rzekę podwoić powrotem na siebie w miejscach i „zwarcia”, tworząc jezioro Ox-Bow w tym procesie. Równowaga między tymi dwoma przeciwstawnymi czynnikami prowadzi do średniego stosunku $π$ między rzeczywistą długością a bezpośrednią odległością między źródłem a ustami.

Zapamiętywanie cyfr

Pifilologia to praktyka zapamiętywania dużej liczby cyfr $π$ , a światowe rekordy są przechowywane w Księgach Rekordów Guinnessa . Rekord zapamiętywania cyfr $π$ , poświadczony przez Guinness World Records, wynosi 70 000 cyfr, wyrecytowany w Indiach przez Rajveera Meenę w ciągu 9 godzin i 27 minut w dniu 21 marca 2015 r. W 2006 r. Akira Haraguchi , emerytowany japoński inżynier, twierdził, że recytował 100 000 miejsc po przecinku, ale twierdzenie nie zostało zweryfikowane przez Księgi Rekordów Guinnessa.

Jedną z powszechnych technik jest zapamiętywanie opowiadania lub wiersza, w którym długość słowa reprezentuje cyfry $π$ : pierwsze słowo ma trzy litery, drugie słowo ma jedną, trzecie ma cztery, czwarte ma jedną, piąte ma pięć i wkrótce. Takie pomoce do zapamiętywania nazywane są mnemonikami . Wczesnym przykładem mnemonika oznaczającego pi, pierwotnie wymyślonego przez angielskiego naukowca Jamesa Jeansa , jest „Jak chcę drinka, oczywiście alkoholika, po ciężkich wykładach dotyczących mechaniki kwantowej”. Kiedy używa się wiersza, czasami określa się go jako piem . Wiersze do zapamiętywania $π$ zostały skomponowane w kilku językach oprócz angielskiego. Rekordowe pamięci $π$ zwykle nie opierają się na wierszach, ale zamiast tego używają metod, takich jak zapamiętywanie wzorców liczbowych i metoda loci .

Kilku autorów użyło cyfr $π$ do ustanowienia nowej formy pisania z ograniczeniami , w której długości słów są wymagane do reprezentowania cyfr $π$ . Cadaeic Cadenza zawiera pierwsze 3835 cyfr $Õ$ w ten sposób, a książka pełnometrażowy Nie Wake zawiera 10.000 słowy, każdy reprezentujący jedną cyfrę $Õ$ .

W kulturze popularnej

Ciasto pi. Ciasta są okrągłe, a „pie” i

π

to homofony , co sprawia, że ciasto jest częstym tematem pi kalamburów .

Być może ze względu na prostotę definicji i wszechobecność we wzorach $π$ jest reprezentowane w kulturze popularnej bardziej niż inne konstrukcje matematyczne.

W koprodukcji dokumentalnej Open University i BBC , The Story of Maths , wyemitowanej w październiku 2008 r. w BBC Four , brytyjski matematyk Marcus du Sautoy pokazuje wizualizację – historycznie pierwszego dokładnego – wzoru obliczania liczby $π$ podczas wizyty w Indiach i odkrywania ich wkład do trygonometrii.

W Palais de la Découverte (muzeum nauki w Paryżu) znajduje się okrągła sala znana jako sala pi . Na jego ściance wpisane jest 707 cyfr $π$ . Cyfry to duże drewniane znaki przymocowane do sufitu przypominającego kopułę. Cyfry zostały oparte na obliczeniach z 1874 r. dokonanych przez angielskiego matematyka Williama Shanksa , które zawierały błąd rozpoczynający się od 528. cyfry. Błąd został wykryty w 1946 roku i poprawiony w 1949 roku.

W powieści Carla Sagana Kontakt sugeruje się, że twórca wszechświata ukrył wiadomość głęboko w cyfrach $π$ . Cyfry $Õ$ również zostały włączone do tekstu do piosenki „PI” z albumu Aerial przez Kate Bush .

W Star Trek epizod Wolf in the Fold , komputer z out-of-kontroli jest zawarty jest polecenie „Compute do ostatniej cyfry wartość $Õ$ ”, choć „ $π$ jest postacią transcendentalna bez rezolucji”.

W Stanach Zjednoczonych Dzień Pi przypada na 14 marca (napisany 14 marca w stylu amerykańskim) i jest popularny wśród studentów. $π$ i jego cyfrowa reprezentacja są często używane przez samozwańczych „ maniaków matematycznych ” do żartów w grupach myślących matematycznie i technologicznie. Kilka okrzyków na uczelni w Massachusetts Institute of Technology to „3.14159”. Dzień Pi w 2015 roku był szczególnie istotny, ponieważ data i godzina 14.03.15 9:26:53 odzwierciedlały znacznie więcej cyfr liczby pi. W niektórych częściach świata, gdzie daty są powszechnie zapisywane w formacie dzień/miesiąc/rok, 22 lipca reprezentuje „dzień aproksymacji liczby pi”, ponieważ 22/7 = 3,142857.

Podczas aukcji w 2011 r. dotyczącej portfela cennych patentów technologicznych firmy Nortel , Google złożył serię niezwykle szczegółowych ofert opartych na stałych matematycznych i naukowych, w tym $π$ .

W 1958 roku Albert Eagle zaproponował zastąpienie $π$ przez $τ$ ( tau ), gdzie $τ = π /2$ , aby uprościć formuły. Jednak żaden inny autor nie używał $τ$ w ten sposób. Niektórzy używają innej wartości, $τ = 2 π = 6,28318...$ , twierdząc, że $τ$ , jako liczba radianów w jednym obrocie , lub jako stosunek obwodu koła do jego promienia, a nie jego średnicy, jest bardziej naturalne niż $π$ i upraszcza wiele formuł. Obchody tej liczby, bo wynosi ona w przybliżeniu 6,28, poprzez uczynienie 28 czerwca „Dniem Tau” i zjedzenie „dwukrotnego tortu”, donosiły media. Jednak to użycie $τ$ nie przeniknęło do matematyki głównego nurtu. Tau zostało dodane do języka programowania Python (jako math.tau) w wersji 3.6

W 1897 roku matematyk-amator próbował przekonać legislaturę Indiany do uchwalenia ustawy Indiana Pi , która opisywała metodę do kwadratu koła i zawierała tekst, który implikował różne nieprawidłowe wartości dla $π$ , w tym 3.2. Projekt ustawy jest znany jako próba ustalenia wartości stałej naukowej poprzez dekret legislacyjny. Ustawa została uchwalona przez Izbę Reprezentantów Indiany, ale odrzucona przez Senat, co oznacza, że nie stała się prawem.

W kulturze komputerowej

We współczesnej kulturze internetowej osoby i organizacje często oddają hołd liczbie $π$ . Na przykład informatyk Donald Knuth pozwolił, by numery wersji jego programu TeX zbliżyły się do $π$ . Wersje to 3, 3.1, 3.14 i tak dalej.

Zobacz też

Bibliografia

Uwagi

Cytaty

Źródła

Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Funkcje specjalne . Cambridge: Wydawnictwo Uniwersyteckie. Numer ISBN 978-0-521-78988-2.
Arndta, Jörga; Haenel, Christoph (2006). Pi uwolnione . Springer-Verlag. Numer ISBN 978-3-540-66572-4. Źródło 5 czerwca 2013 . Tłumaczenie na język angielski autorstwa Catriony i Davida Lischki.
Ayers, Frank (1964). Rachunek . McGraw-Hill. Numer ISBN 978-0-07-002653-7.
Bailey, David H.; Plouff, Szymon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). „Poszukiwanie PI”. Inteligencja matematyczna . 19 (1): 50–56. CiteSeerX 10.1.1.138.7085 . doi : 10.1007/BF03024340 . ISSN 0343-6993 . S2CID 14318695 .
Beckmann, Peter (1989) (1974). Historia Pi . Prasa św. Numer ISBN 978-0-88029-418-8.
Berggren, Lennart; Borwein, Jonathan ; Borwein, Piotr (1997). Pi: Księga Źródłowa . Springer-Verlag. Numer ISBN 978-0-387-20571-7.
Boeing, Niels (14 marca 2016). „Die Welt ist Pi” [Świat to Pi]. Zeit Online (w języku niemieckim). Zarchiwizowane z oryginału w dniu 17 marca 2016 r. Die Ludolphsche Zahl oder Kreiszahl erhielt nun auch das Symbol, unter dem wir es heute kennen: William Jones schlug 1706 den griechischen Buchstaben π vor, in Anlehnung an perimetros, griechisch für Umfang Leonhard Euler etablierte π schließlich in seinen mathematischen Schriften. [Liczba ludolfijska lub liczba okręgu otrzymała teraz także symbol, pod którym znamy ją dzisiaj: William Jones zaproponował w 1706 grecką literę π, opartą na perimetros [περίμετρος], po grecku oznaczającą obwód. Leonhard Euler mocno ustanowił π w swoich pismach matematycznych.]
Borwein, Jonathan; Borwein, Piotr (1987). Pi i AGM: studium teorii liczb analitycznych i złożoności obliczeniowej . Wileya. Numer ISBN 978-0-471-31515-5.
Boyer, Carl B.; Merzbach, Uta C. (1991). Historia matematyki (2 wyd.). Wileya. Numer ISBN 978-0-471-54397-8.
Bronshteĭn, Ilia; Semendiajew, KA (1971). Przewodnik po matematyce . Verlag Harri Deutsch . Numer ISBN 978-3-87144-095-3.
Eymard, Pierre; Lafon, Jean Pierre (1999). Liczba Pi . Amerykańskie Towarzystwo Matematyczne. Numer ISBN 978-0-8218-3246-2., tłumaczenie na język angielski przez Stephena Wilsona.
Gupta, RC (1992). „Na pozostałym terminie w serii Madhava-Leibniza” . Ganitę Bharati . 14 (1–4): 68–71.
Howe, Roger (1980), „O roli grupy Heisenberga w analizie harmonicznej”, Biuletyn Amerykańskiego Towarzystwa Matematycznego , 3 (2): 821-844, doi : 10.1090/S0273-0979-1980-14825-9 , MR 0578375.
Józef, George Gheverghese (1991). Herb pawia: pozaeuropejskie korzenie matematyki . Wydawnictwo Uniwersytetu Princeton. Numer ISBN 978-0-691-13526-7. Źródło 5 czerwca 2013 .
Posamentier, Alfred S.; Lehmann, Ingmar (2004). Pi: Biografia najbardziej tajemniczego numeru na świecie . Księgi Prometeusza. Numer ISBN 978-1-59102-200-8.
Reitwiesner, George (1950). „An ENIAC Oznaczanie pi i e do 2000 miejsc dziesiętnych”. Tabele matematyczne i inne pomoce do obliczeń . 4 (29): 11–15. doi : 10.2307/2002695 . JSTOR 2002695 .
Remmert, Reinhold (2012). „Rozdz. 5 Co to jest π?” . W Heinz-Dieter Ebbinghaus; Hansa Hermesa; Friedricha Hirzebrucha; Maxa Koechera; Klausa Mainzera; Jürgen Neukirch; Aleksander Prestel; Reinhold Remmert (red.). Liczby . Skoczek. Numer ISBN 978-1-4612-1005-4.
Rossi, Corinna (2004). Architektura i matematyka w starożytnym Egipcie . Cambridge: Wydawnictwo Uniwersyteckie. Numer ISBN 978-1-107-32051-2.
Roy, Ranjan (1990). „Odkrycie Formuły serii dla pi przez Leibniza, Gregory'ego i Nilakantha”. Magazyn Matematyka . 63 (5): 291–306. doi : 10.2307/2690896 . JSTOR 2690896 .
Schepler, HC (1950). „Chronologia Pi”. Magazyn Matematyka . 23 (3): 165–170 (sty/luty), 216–228 (mar/kwiecień) i 279–283 (maj/czerwiec). doi : 10.2307/3029284 . JSTOR 3029284 .. numer 3 styczeń/luty , numer 4 marzec/kwiecień , numer 5 maj/czerwiec
Thompson, William (1894), "Problemy izoperimetryczne", Nature Series: Popularne wykłady i adresy , II : 571-592

Dalsza lektura

Blatner, David (1999). Radość Pi . Walker i firma. Numer ISBN 978-0-8027-7562-7.
Borwein, Jonathan ; Borwein, Piotr (1984). „Średnia arytmetyczno-geometryczna i szybkie obliczanie funkcji elementarnych” (PDF) . Przegląd SIAM . 26 (3): 351–365. CiteSeerX 10.1.1.218.8260 . doi : 10.1137/1026073 .
Borwein, Jonathan; Borwein, Piotr; Bailey, David H. (1989). „Ramanujan, równania modułowe i przybliżenia do liczby Pi lub jak obliczyć miliard cyfr liczby Pi”. American Mathematical Monthly (Przesłany rękopis). 96 (3): 201–219. doi : 10.2307/2325206 . JSTOR 2325206 .
Chudnovsky, David V. i Chudnovsky, Gregory V. , „Aproksymacje i mnożenie złożone według Ramanujan”, w Ramanujana Revisited (GE Andrews i in. Eds), Academic Press, 1988, s. 375-396, 468-472
Cox, David A. (1984). „Średnia arytmetyczno-geometryczna Gaussa”. L'Enseignement Mathématique . 30 : 275–330.
Delahaye, Jean-Paul (1997). Le Fascinant Nombre Pi . Paryż: Bibliothèque Pour la Science. Numer ISBN 2-902918-25-9.
Engels, Hermann (1977). „Kwadratura koła w starożytnym Egipcie” . Historia Matematyka . 4 (2): 137–140. doi : 10.1016/0315-0860(77)90104-5 .
Euler, Leonhard , „O wykorzystaniu odkrytych ułamków do sumowania serii nieskończonych”, we Wstępie do analizy nieskończoności. Księga I , przekład z łaciny JD Blanton, Springer-Verlag, 1964, s. 137–153
Hardy, GH; Wright, EM (2000). Wprowadzenie do teorii liczb (wyd. piąte). Oksford, Wielka Brytania: Clarendon Press.
Heath, TL, Dzieła Archimedesa , Cambridge, 1897; przedrukowane w The Works of Archimedes with The Method of Archimedes , Dover, 1953, s. 91-98
Huygens, Christiaan , "De Circuli Magnitudine Inventa", Christiani Hugenii Opera Varia I , Leiden 1724, s. 384-388
Lay-Yong, Lam ; Tian-Se, Ang (1986). „Pomiary kołowe w starożytnych Chinach” . Historia Matematyka . 13 (4): 325–340. doi : 10.1016/0315-0860(86)90055-8 .
Lindemann, Ferdynand (1882). „Ueber die Zahl pi” . Matematyka Annalen . 20 (2): 213–225. doi : 10.1007/bf01446522 . S2CID 120469397 . Zarchiwizowane od oryginału w dniu 22 stycznia 2015 r.
Matar, K. Mukunda; Rajagonal, C. (1944). „On the Hindu Quadrature of the Circle” (dodatek K. Balagangadharan)” Journal of Bombay Branch of the Royal Asiatic Society . 20 : 77-82.
Niwen, Iwan (lipiec 1947). „Prosty dowód, że pi jest irracjonalne” . Biuletyn Amerykańskiego Towarzystwa Matematycznego . 53 (7): 507. doi : 10.1090/S0002-9904-1947-08821-2 .
Ramanujan, Srinivasa (1914). „Równania modułowe i przybliżenia do π”. Kwartalnik Matematyki Czystej i Stosowanej . XLV : 350-372.Przedruk w Ramanujan, Srinivasa (2015) [1927]. Hardy, GH; Seshu Aiyar, PV; Wilson, BM (red.). Srinivasa Ramanujan: Zebrane dokumenty . Wydawnictwo Uniwersytetu Cambridge. s. 23–29. Numer ISBN 978-1-107-53651-7.
Shanks, William , Składki do matematyki zawierające głównie sprostowanie koła do 607 miejsc dziesiętnych , 1853, s. i-xvi, 10
Shanks, Daniel ; Klucz, John William (1962). „Obliczanie liczby pi do 100 000 dziesiętnych” . Matematyka Obliczeń . 16 (77): 76–99. doi : 10.1090/s0025-5718-1962-0136051-9 .
Tropfke, Johannes (1906). Geschichte Der Elementar-Mathematik in Systematischer Darstellung [ Historia matematyki elementarnej ] (w języku niemieckim). Lipsk: Verlag Von Veit.
Viete, Francois , Variorum de Rebus Mathematicis Reponsorum Liber VII. F. Viete, Opera Mathematica (przedruk), Georg Olms Verlag, 1970, s. 398-401, 436-446
Wagon, Stan (1985). „Czy Pi jest normalne?”. Inteligencja matematyczna . 7 (3): 65-67. doi : 10.1007/BF03025811 . S2CID 189884448 .
Wallis, Jan (1655-1656). Arithmetica Infinitorum, sive Nova Methodus Inquirendi in Curvilineorum Quadratum, aliaque difficiliora Matheseos Problemata (po łacinie). Oksford.Przedruk w Opera Mathematica . 1 . Oksford: E Theatro Sheldoniano. 1695. s. 357-478.
Żebrowski, Ernest (1999). Historia koła: rozumowanie matematyczne i wszechświat fizyczny . Wydawnictwo Uniwersytetu Rutgersa. Numer ISBN 978-0-8135-2898-4.

Zewnętrzne linki

10 milionów miejsc po przecinku
„Pi” w Wolfram Mathworld
Reprezentacje Pi w Wolfram Alpha
Wykazanie przez Lamberta (1761) irracjonalności $π$ , online i analizowane BibNum (PDF).
Wyszukiwarka $π$ 2 miliardy możliwych do przeszukiwania cyfr $π$ , $e$ oraz √ 2

Languages

In other projects