Wielokąt foremny — Regular polygon

Zestaw wypukłych regularnych n-gonów
Wielokąty regularne
Krawędzie i wierzchołki	n
Symbol Schläfli	{ n }
Wykres Coxetera-Dynkina
Grupa symetrii	D n , rząd 2n
Podwójny wielokąt	Samodzielność
Powierzchnia (z długością boku, s )	${\ Displaystyle A = {\ tfrac {1} {4}} ns ^ {2} \ łóżeczko \ po lewej ({\ Frac {\ pi {n}} \ po prawej)}$
Kąt wewnętrzny	${\ Displaystyle (n-2) \ razy {\ Frac {180 ^ {\ circ}} {n}}}$
Suma kątów wewnętrznych	${\ Displaystyle \ lewo (n-2 \ prawo) \ razy 180 ^ {\ circ}}$
Wpisana średnica koła	${\ Displaystyle d_ {\ tekst {IC}} = s \ łóżeczko \ lewo ({\ Frac {\ pi} {n}} \ prawej)}$
Średnica okręgu opisanego	${\ Displaystyle d_ {\ tekst {OC}} = s \ csc \ lewo ({\ Frac {\ pi} {n}} \ po prawej)}$
Nieruchomości	Wypukły , cykliczny , równoboczny , izogonalny , izotoksal

W geometrii euklidesowej , o wielokąt foremny to wielokąt czyli równokątny (wszystkie kąty są równe miary) oraz równoboczny (wszystkie boki mają taką samą długość). Wielokąty regularne mogą być wypukłe lub gwiaździste . W granicy ciąg wielokątów foremnych o rosnącej liczbie boków przybliża okrąg , jeśli obwód lub obszar jest stały, lub apeirogon foremny (efektywnie linia prosta ), jeśli długość krawędzi jest stała.

Właściwości ogólne

Regularne wielokąty wypukłe i gwiaździste z 3 do 12 wierzchołkami oznaczonymi symbolami Schläfliego

Te właściwości dotyczą wszystkich regularnych wielokątów, zarówno wypukłych, jak i gwiaździstych .

Regularne n -sided wielokąt ma symetrii obrotowej o uporządkowaniu n .

Wszystkie wierzchołki wielokąta foremnego leżą na wspólnym okręgu ( okrąg opisanym ); tj. są to punkty koncykliczne . Oznacza to, że wielokąt foremny jest wielokątem cyklicznym .

Wraz z majątku równa długości boków, oznacza to, że każdy wielokąt foremny ma również koła wpisanego lub incircle , która jest styczna do każdej strony w punkcie środkowym. Tak więc wielokąt foremny jest wielokątem stycznym .

Regularne n -sided wielokąta może być wykonana z kompasu i liniału wtedy i tylko wtedy, gdy nieparzyste głównymi czynnikami n są różnymi liczbami pierwszymi Fermat . Zobacz wielokąt możliwy do zbudowania .

Symetria

Grupa symetrii o n -sided regularny wielokąt dwuściennej grupy D _N (rzędu 2 N ): R ₂ , D ₃ , D ₄ , ... składają się z obrotami w C _n , wraz z symetria osiowa w n osiach które przechodzą przez centrum. Jeśli n jest parzyste, to połowa tych osi przechodzi przez dwa przeciwległe wierzchołki, a druga połowa przez środek przeciwległych boków. Jeśli n jest nieparzyste, wszystkie osie przechodzą przez wierzchołek i środek przeciwnej strony.

Regularne wielokąty wypukłe

Wszystkie regularne proste wielokąty ( wielokąt prosty to taki, który nigdzie się nie przecina) są wypukłe. Te, które mają taką samą liczbę boków, są również podobne .

N -sided wypukłego wielokąta foremnego jest oznaczona jej symbol schläfliego { n }. Dla n < 3 mamy dwa przypadki zdegenerowane :

Monogon {1}

Zwyrodniać w zwykłej przestrzeni . (Większość autorytetów nie uważa monogonu za prawdziwy wielokąt, częściowo z tego powodu, a także dlatego, że poniższe formuły nie działają, a jego struktura nie przypomina żadnego abstrakcyjnego wielokąta .)

Digon {2}; „podwójny segment linii”

Zwyrodniać w zwykłej przestrzeni . (Niektóre autorytety z tego powodu nie uważają digonu za prawdziwy wielokąt).

W pewnych kontekstach wszystkie rozważane wielokąty będą regularne. W takich okolicznościach zwyczajowo opuszcza się przedrostek regularny. Na przykład wszystkie ściany jednostajnych wielościanów muszą być regularne, a ściany będą opisywane po prostu jako trójkąt, kwadrat, pięciokąt itp.

Kąty

Dla regularnego wypukłego n- kąta każdy kąt wewnętrzny ma miarę:

${\ Displaystyle {\ Frac {180 (n-2)} {n}}}$ stopnie;

${\displaystyle {\frac {(n-2)\pi}{n}}}$radiany; lub

${\ Displaystyle {\ Frac {(n-2)} {2n}}}$pełne obroty ,

a każdy kąt zewnętrzny (tj. uzupełniający do kąta wewnętrznego) ma miarę stopni, z sumą kątów zewnętrznych równą 360 stopni lub 2π radianów lub jeden pełny obrót. ${\ Displaystyle {\ tfrac {360} {n}}}$

Gdy n zbliża się do nieskończoności, kąt wewnętrzny zbliża się do 180 stopni. Dla wielokąta foremnego o 10 000 bokach ( miriagon ) kąt wewnętrzny wynosi 179,964°. Wraz ze wzrostem liczby boków kąt wewnętrzny może zbliżyć się do 180°, a kształt wielokąta zbliża się do koła. Jednak wielokąt nigdy nie może stać się okręgiem. Wartość kąta wewnętrznego nigdy nie może być dokładnie równa 180°, ponieważ obwód w rzeczywistości stałby się linią prostą. Z tego powodu okrąg nie jest wielokątem o nieskończonej liczbie boków.

Przekątne

Dla n > 2 liczba przekątnych wynosi ; tj. 0, 2, 5, 9, ..., dla trójkąta, kwadratu, pięciokąta, sześciokąta, ... . Przekątne dzielą wielokąt na 1, 4, 11, 24, ... części OEIS :  A007678 . ${\displaystyle {\tfrac {1}{2}}n(n-3)}$

Dla regularnego n- kąta wpisanego w okrąg o jednostkowym promieniu iloczyn odległości od danego wierzchołka do wszystkich innych wierzchołków (w tym wierzchołków sąsiednich i wierzchołków połączonych przekątną) wynosi n .

Punkty w samolocie

Dla zwykłego prostego n -gonu o promieniu okręgu R i odległościach d _i od dowolnego punktu na płaszczyźnie do wierzchołków mamy

${\ Displaystyle {\ Frac {1} {n}} \ suma _ {i = 1} ^ {n} d_ {i} ^ {4} + 3R ^ {4} = \ lewo ({\ Frac {1} { n}}\sum _{i=1}^{n}d_{i}^{2}+R^{2}\right)^{2}.}$

Dla większych potęg odległości od dowolnego punktu na płaszczyźnie do wierzchołków regularnego -gonu, jeśli ${\displaystyle d_{i}}$${\ Displaystyle n}$

${\ Displaystyle S_ {n} ^ {(2 m)} = {\ Frac {1} {n}} \ suma _ {i = 1} ^ {n} d_ {i} ^ {2 m}}$,

następnie

${\ Displaystyle S_ {n} ^ {(2m)} = \ lewo (S_ {n} ^ {(2)} \ prawej) ^ {m} + \ suma _ {k = 1} ^ {\ lewo \ l piętro { \frac {m}{2}}\right\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R^{2k}\left(S_{n}^{(2 )}-R^{2}\right)^{k}\left(S_{n}^{(2)}\right)^{m-2k}}$,

oraz

${\ Displaystyle S_ {n} ^ {(2m)} = \ lewo (S_ {n} ^ {(2)} \ prawo) ^ {m} + \ suma _ {k = 1} ^ {\ lewo \ l piętro { \frac {m}{2}}\right\rfloor }{\frac {1}{2^{k}}}{\binom {m}{2k}}{\binom {2k}{k}}\left (S_{n}^{(4)}-\left(S_{n}^{(2)}\right)^{2}\right)^{k}\left(S_{n}^{(2 )}\right)^{m-2k}}$,

gdzie jest dodatnią liczbą całkowitą mniejszą niż . ${\ Displaystyle m}$${\ Displaystyle n}$

Jeśli jest odległością od dowolnego punktu na płaszczyźnie do środka ciężkości regularnego gonu o promieniu okręgu , to ${\ Displaystyle L}$${\ Displaystyle n}$${\ Displaystyle R}$

${\ Displaystyle \ suma _ {i = 1} ^ {n} d_ {i} ^ {2 m} = n \ lewo (\ lewo (R ^ {2} + L ^ {2} \ po prawej) ^ {m} + \sum _{k=1}^{\left\lfloor {\frac {m}{2}}\right\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R ^{2k}L^{2k}\left(R^{2}+L^{2}\right)^{m-2k}\right)}$,

gdzie = 1, 2, …, . ${\ Displaystyle m}$${\displaystyle n-1}$

Punkty wewnętrzne

Dla regularnego n- kąta suma odległości prostopadłych od dowolnego punktu wewnętrznego do n boków jest n razy apotem (apotem jest odległością od środka do dowolnego boku). Jest to uogólnienie twierdzenia Vivianiego dla przypadku n = 3.

Circumpromień

Regularnego pięciokąta ( n = 5) z boku s , circumradius R i apotema

Wykresy boczne ,  s ; apotem ,  a ; i obszar ,  z regularnych wielokątów o n bokach i circumradius 1, z podstawy ,  b z prostokąta o tej samej powierzchni . Zielona linia pokazuje przypadek n = 6 .

Circumradius R od środka regularnego wielokąta do jednego z wierzchołków jest uzależniona od długości boku a lub w apotema a przez

${\ Displaystyle R = {\ Frac {s} {2 \ sin \ lewo ({\ Frac {\ pi}} \ prawej)}} = {\ Frac {a} {\ cos \ lewo ({\ Frac {\pi }{n}}\prawo)}}}$

Dla konstruowalnych wielokątów , algebraicznymi wyrażenia dla tych relacji istnieje; zobacz Wielokąt dwucentryczny#Wielokąty regularne .

Suma prostopadłych od wierzchołków n- kąta foremnego do dowolnej prostej stycznej do okręgu opisanego jest równa n- krotności promienia okręgu.

Suma kwadratów odległości od wierzchołków regularnego n- kąta do dowolnego punktu na jego okręgu wynosi 2 nR ^2, gdzie R jest promieniem okręgu.

Suma kwadratów odległości od punktów środkowych boków regularnego n- kąta do dowolnego punktu na okręgu wynosi 2 nR ² −1/4ns ² , gdzie s to długość boku, a R to promień okręgu.

Jeśli są odległościami od wierzchołków kąta foremnego do dowolnego punktu na jego okręgu, to ${\displaystyle d_{i}}$${\ Displaystyle n}$

${\ Displaystyle 3 \ lewo (\ suma _ {i = 1} ^ {n} d_ {i} ^ {2} \ prawej) ^ {2} = 2 n \ suma _ {i = 1} ^ {n} d_ { ja}^{4}}$.

Sekcje

Coxeter stwierdza, że ​​każdy zonogon (2 m -gon, którego przeciwległe boki są równoległe i równej długości) może być rozcięty na lub${\displaystyle {\tbinom {n}{2}}}$1/2m ( m − 1) równoległoboki. Te kafelki są zawarte jako podzbiory wierzchołków, krawędzi i ścian w rzutach ortogonalnych m -sześciany . W szczególności dotyczy to regularnych wielokątów o równomiernie wielu bokach, w którym to przypadku wszystkie równoległoboki są rombami. Lista OEIS :  A006245 podaje liczbę rozwiązań dla mniejszych wielokątów.

Przykładowe przekroje dla wybranych równobocznych wielokątów foremnych

2 mln	6	8	10	12	14	16	18	20	24	30	40	50
Obraz
Romby	3	6	10	15	21	28	36	45	66	105	190	300

Powierzchnia

Pole A wypukłego wielokąta n- bocznego foremnego mającego boki s , obwód promienia R , apotem a i obwód p jest określone wzorem

${\ Displaystyle A = {\ tfrac {1} {2}} nsa = {\ tfrac {1} {2}} pa = {\ tfrac {1} {4}} ns ^ {2} \ łóżeczko \ lewo ({{ \tfrac {\pi }{n}}\right)=na^{2}\tan \left({\tfrac {\pi }{n}}\right)={\tfrac {1}{2}}nR ^{2}\sin \left({\tfrac {2\pi }{n}}\right)}$

W przypadku regularnych wielokątów z boku a = 1, circumradius R = 1 lub apotema = 1, to wytwarza się w poniższej tabeli: (Należy zauważyć, że ponieważ jako obszar, gdy dąży się do jak rośnie duży). ${\ Displaystyle \ łóżeczko x \ rightarrow 1/x}$${\displaystyle x\rightarrow 0}$${\displaystyle s=1}$${\ Displaystyle n ^ {2}/4 \ pi}$${\ Displaystyle n}$

Liczba boków	Powierzchnia, gdy bok s = 1		Pole, w którym obwód promienia R = 1			Pole, gdy apotem a = 1
	Dokładny	Przybliżenie	Dokładny	Przybliżenie	W stosunku do obszaru wokół okręgu	Dokładny	Przybliżenie	W stosunku do obszaru otaczającego
n	${\ Displaystyle {\ tfrac {n} {4}} \ łóżeczko \ po lewej ({\ tfrac {\ pi} {n}} \ po prawej)}$		${\ Displaystyle {\ tfrac {n} {2}} \ grzech \ po lewej ({\ tfrac {2 \ pi} {n}} \ po prawej)}$		${\ Displaystyle {\ tfrac {n} {2 \ pi}} \ grzech \ po lewej ({\ tfrac {2 \ pi} {n}} \ po prawej)}$	${\ Displaystyle n \ tan \ po lewej ({\ tfrac {\ pi} {n}} \ po prawej)}$		${\ Displaystyle {\ tfrac {n} {\ pi}} \ tan \ po lewej ({\ tfrac {\ pi} {n}} \ po prawej)}$
3	${\displaystyle {\tfrac {\sqrt {3}}{4}}}$	0,433012702	${\displaystyle {\tfrac {3{\sqrt {3}}}{4}}}$	1.299038105	0,4134966714	${\displaystyle 3{\sqrt {3}}}$	5.196152424	1,653986686
4	1	1.0000000000	2	2.00000000	0,6366197722	4	4.000000000	1,273239544
5	${\displaystyle {\tfrac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}}$	1.720477401	${\ Displaystyle {\ tfrac {5} {4}}{\ sqrt {{\ tfrac {1} {2}} \ lewo (5 + {\ sqrt {5}} \ po prawej)}}}$	2.377641291	0.7568267288	${\displaystyle 5{\sqrt {5-2{\sqrt {5}}}}}$	3.632712640	1.156328347
6	${\displaystyle {\tfrac {3{\sqrt {3}}}{2}}}$	2.598076211	${\displaystyle {\tfrac {3{\sqrt {3}}}{2}}}$	2.598076211	0,8269933428	${\displaystyle 2{\sqrt {3}}}$	3.464101616	1.102657791
7		3.633912444		2.736410189	0,8710264157		3.371022333	1.073029735
8	${\displaystyle 2+2{\sqrt {2}}}$	4.828427125	${\displaystyle 2{\sqrt {2}}}$	2.828427125	0.9003163160	${\ Displaystyle 8 \ lewo ({\ sqrt {2}}-1 \ po prawej)}$	3,313708500	1.054786175
9		6.181824194		2.892544244	0,9207254290		3,275732109	1.042697914
10	${\ Displaystyle {\ tfrac {5} {2}} {\ sqrt {5 + 2 {\ sqrt {5}}}}}$	7.694208843	${\displaystyle {\tfrac {5}{2}}{\sqrt {{\tfrac {1}{2}} \ lewo (5-{\ sqrt {5}} \ prawej)}}}$	2,938926262	0,9354892840	${\displaystyle 2{\sqrt {25-10{\sqrt {5}}}}}$	3.249196963	1.034251515
11		9.365639907		2.973524496	0,9465022440		3.229891423	1.028106371
12	${\displaystyle 6+3{\sqrt {3}}}$	11.19615242	3	3.0000000000	0,9549296586	${\ Displaystyle 12 \ lewo (2-{\ sqrt {3}} \ po prawej)}$	3.215390309	1.023490523
13		13.18576833		3.020700617	0.9615188694		3.204212220	1.019932427
14		15.33450194		3.037186175	0,9667663859		3.195408642	1.017130161
15		17.64236291		3.050524822	0.9710122088		3.188348426	1.014882824
16		20.10935797	${\ Displaystyle 4 {\ sqrt {2-{\ sqrt {2}}}}}$	3.061467460	0.9744953584		3.182597878	1.013052368
17		22.73549190		3.070554163	0.9773877456		3.177850752	1.011541311
18		25.52076819		3.078181290	0.9798155361		3.173885653	1.010279181
19		28.46518943		3.084644958	0.9818729854		3.170539238	1.009213984
20		31.56875757		3.090169944	0,9836316430		3.167688806	1.008306663
100		795.5128988		3.139525977	0,9993421565		3.142626605	1,000329117
1000		79577,20975		3.141571983	0.9999934200		3.141602989	1,000003290
10 000		7957746.893		3.141592448	0.9999999345		3.141592757	1.00000033
1 000 000		79577471545		3.141592654	1.0000000000		3.141592654	1.0000000000

Porównanie rozmiarów wielokątów foremnych o tej samej długości krawędzi, od trzech do sześćdziesięciu boków. Rozmiar rośnie bez ograniczeń, gdy liczba boków zbliża się do nieskończoności.

Ze wszystkich n- gonów o danym obwodzie, ten o największej powierzchni jest regularny.

Konstruowany wielokąt

Niektóre regularne wielokąty są łatwe do skonstruowania za pomocą kompasu i linijki ; inne regularne wielokąty nie są w ogóle możliwe do zbudowania. W starożytnych greckich matematyków umiał zbudować regularny wielobok z 3, 4 lub 5 stron, a oni wiedzieli, jak skonstruować wielokąt foremny z podwójną liczbą stronach danego wielokąta foremnego. Doprowadziło to do postawienia pytania: czy za pomocą kompasu i linijki można skonstruować wszystkie regularne n- gony? Jeśli nie, to które n- gony są możliwe do zbudowania, a które nie?

Carl Friedrich Gauss dowiódł możliwości budowy regularnego 17-gonu w 1796 roku. Pięć lat później rozwinął teorię okresów Gaussa w swoich Disquisitiones Arithmeticae . Teoria ta pozwoliła mu sformułować warunek wystarczający dla konstruowalności wielokątów foremnych:

Regularny n- gon może być skonstruowany za pomocą kompasu i liniału pomiarowego, jeśli n jest iloczynem potęgi 2 i dowolnej liczby różnych liczb pierwszych Fermata (w tym żadnej).

(Liczba pierwsza Fermata jest liczbą pierwszą w postaci ) Gauss stwierdził bez dowodu, że ten warunek jest również konieczny , ale nigdy nie opublikował swojego dowodu. Pełny dowód konieczności podał Pierre Wantzel w 1837 roku. Wynik ten znany jest jako twierdzenie Gaussa-Wantzela . ${\ Displaystyle 2 ^ {(2 ^ {n})} + 1.}$

Równoważnie, regularny n- gon jest konstruowalny wtedy i tylko wtedy, gdy cosinus jego wspólnego kąta jest liczbą konstruktywną — to znaczy może być zapisany w kategoriach czterech podstawowych operacji arytmetycznych i wyciągania pierwiastków kwadratowych.

Regularne wielokąty skośne

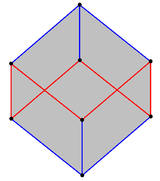Kostka zawiera pochylać regularny sześciokąt , postrzegane jako 6 czerwonych krawędziach zygzakiem między dwóch płaszczyznach prostopadłych do osi przekątnej sześcianu.

Zygzakowate krawędzie boczne n - antypryzmaty reprezentują regularny skos 2 n- kąt, jak pokazano na tym 17-kątnym antypryzmacie.

Regularny wielokąt skośny w przestrzeni 3-wymiarowej może być postrzegane jako nie płaskie ścieżki zygzakiem dwóch równoległych płaszczyznach, zdefiniowane jako bocznych krawędziach jednolitej antygraniastosłup . Wszystkie krawędzie i kąty wewnętrzne są równe.

W Platońskie ciało stałe (the Tetrahedron , sześcian , ośmiościan , dwunastościan i dwudziestościanu ) mają wielokątów Petriego, widoczne na czerwony tutaj, z boków 4, 6, 6, 10 i 10, odpowiednio.

Bardziej ogólnie regularne wielokąty skośne można zdefiniować w n -przestrzeni. Przykłady obejmują wieloboki Petriego wielokątny ścieżki krawędzi, które dzielą się regularne Polytope na dwie połowy, i uważanych za regularnego wielokąta w rzucie prostokątnym.

W nieskończonej granicy skośne wielokąty regularne stają się skośnymi apeirogonami .

Regularne wielokąty gwiazdy

Regularne wielokąty gwiazdy

2 < 2q < p, gcd (p, q) = 1 {5/2} {7/2} {7/3} ...
Symbol Schläfli	{p/k}
Wierzchołki i krawędzie	P
Gęstość	Q
Schemat Coxetera
Grupa symetrii	Dwuścienny (D p )
Podwójny wielokąt	Samodzielność
Kąt wewnętrzny ( stopnie )	${\displaystyle {\frac {180(p-2q)}{p}}}$

Niewypukły wielokąt foremny to wielokąt foremny gwiazdy . Najczęstszym przykładem jest pentagram , który ma te same wierzchołki co pięciokąt , ale łączy naprzemienne wierzchołki.

W przypadku n- bocznego wielokąta gwiazdy, symbol Schläfliego jest modyfikowany, aby wskazać gęstość lub „gwiaździstość” m wielokąta, jako { n / m }. Jeśli na przykład m wynosi 2, to co drugi punkt jest łączony. Jeśli m wynosi 3, to co trzeci punkt jest łączony. Granica wielokąta wije się wokół środka m razy.

(niezdegenerowane) regularne gwiazdy o maksymalnie 12 bokach to:

• Pentagram – {5/2}
• Heptagram – {7/2} i {7/3}
• Oktagram – {8/3}
• Enneagram – {9/2} i {9/4}
• Dekagram – {10/3}
• Hendekagram – {11/2}, {11/3}, {11/4} i {11/5}
• Dodekagram – {12/5}

m i n musi być względnie pierwsze , a liczba ta degeneracji.

Zdegenerowane regularne gwiazdy o maksymalnie 12 bokach to:

• Czworokąt – {4/2}
• Sześciokąty – {6/2}, {6/3}
• Ośmiokąty – {8/2}, {8/4}
• Enneagon – {9/3}
• Dziesięciokąty — {10/2}, {10/4} i {10/5}
• Dwunastokąty – {12/2}, {12/3}, {12/4} i {12/6}

Dwie interpretacje {6/2}

Grünbaum {6/2} lub 2{3}	Coxeter 2 {3} lub {6}[2{3}]{6}
Sześciokąt podwójnie nawinięty	Heksagram jako związek dwóch trójkątów

W zależności od dokładnego wyprowadzenia symbolu Schläfli, opinie co do charakteru zdegenerowanej postaci są różne. Na przykład {6/2} można traktować na dwa sposoby:

• Przez większą część XX wieku (patrz na przykład Coxeter (1948) ) powszechnie przyjmowaliśmy /2, aby wskazać łączenie każdego wierzchołka wypukłego {6} z jego najbliższymi sąsiadami dwa kroki dalej, aby uzyskać regularny związek dwóch trójkątów lub heksagram .
  Coxeter wyjaśnia ten regularny związek za pomocą notacji {kp}[k{p}]{kp} dla związku {p/k}, więc heksagram jest reprezentowany jako {6}[2{3}]{6}. W bardziej zwięzły sposób Coxeter pisze również 2 {n/2}, jak 2 {3} dla heksagramu jako złożonego jako naprzemian regularnych wielokątów parzystych, z kursywą na wiodącym czynniku, aby odróżnić go od zbieżnej interpretacji.
• Wielu współczesnych geometrów, takich jak Grünbaum (2003), uważa to za błędne. Przyjmują /2, aby wskazać przesuwanie dwóch miejsc wokół {6} na każdym kroku, uzyskując trójkąt „podwójnie nawinięty”, który ma dwa wierzchołki nałożone na każdy punkt narożny i dwie krawędzie wzdłuż każdego odcinka linii. Nie tylko lepiej pasuje to do współczesnych teorii abstrakcyjnych wielokątów , ale także dokładniej odwzorowuje sposób, w jaki Poinsot (1809) stworzył swoje wielokąty gwiaździste – biorąc pojedynczy odcinek drutu i zginając go w kolejnych punktach pod tym samym kątem. aż postać się zamknie.

Dualizm regularnych wielokątów

Wszystkie regularne wielokąty są self-dualny do spójnością, a dla nieparzystych n są self-dualny do tożsamości.

Ponadto regularne figury gwiazd (związki), składające się z regularnych wielokątów, są również samo-dwójne.

Wielokąty regularne jako ściany wielościanów

Jednolity wielościan ma regularne wielokąty jak twarze, takie, że dla każdych dwóch wierzchołków istnieje izometria jeden mapowanie do drugiego (tak jak nie ma dla wielokąta foremnego).

Quasiregular wielościan jest jednolity wielościan, który ma tylko dwa rodzaje twarzy na przemian wokół każdego wierzchołka.

Regularne wielościan jest jednolity wielościan, który ma tylko jeden rodzaj twarzy.

Pozostałe (niejednolite) wypukłe wielościany o regularnych ścianach są znane jako bryły Johnsona .

Wielościan posiadający regularne trójkąty jako twarze nazywa się deltahedron .

Zobacz też

• Dachówki euklidesowe przez wypukłe wielokąty regularne
• Bryła platońska
• Apeirogon – Wielokąt o nieskończonych bokach może być również regularny, {∞}.
• Lista regularnych politopów i związków
• Wielokąt równoboczny
• Koło Carlyle'a

Uwagi

Bibliografia

• Coxeter, HSM (1948). „Zwykłe Polytopes”. Methuen i spółka Cytowanie dziennika wymaga |journal=( pomoc )
• Grünbauma, B.; Czy twój wielościan jest taki sam jak mój wielościan?, Dyskretny i komputerowy. geom: pismo Goodmana-Pollacka , wyd. Aronov i in., Springer (2003), s. 461–488.
• Poinsot, L .; Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9 (1810), s. 16-48.

Zewnętrzne linki

• Weisstein, Eric W. "Wielokąt regularny" . MatematykaŚwiat .
• Opis wielokąta regularnego Z interaktywną animacją
• Okrąg regularnego wielokąta z interaktywną animacją
• Obszar regularnego wielokąta Trzy różne formuły z interaktywną animacją
• Renesansowe konstrukcje wielokątów foremnych artystów w Convergence