Wielościan regularny - Regular polyhedron

Regularne wielościan jest wielościan , którego symetria grupa działa na jego przechodni flagi . Wielościan foremny jest wysoce symetryczny, ponieważ wszystkie są przechodnie krawędziowe , wierzchołki przechodnie i ścianki przechodnie . W kontekstach klasycznych stosuje się wiele różnych równoważnych definicji; częstym jest to, że ściany są przystającymi regularnymi wielokątami, które są ułożone w ten sam sposób wokół każdego wierzchołka .

Wielościan foremny jest identyfikowany przez jego symbol Schläfliego w postaci { n , m }, gdzie n jest liczbą boków każdej ściany, a m liczbą ścian spotykających się w każdym wierzchołku. Istnieje 5 skończonych wypukłych wielościanów regularnych ( bryła platońska ) i cztery regularne wielościany gwiaździste ( wielościany Keplera-Poinsota ), co daje w sumie dziewięć regularnych wielościanów. Ponadto istnieje pięć regularnych związków wielościanów regularnych.

Wielościany regularne

Istnieje pięć wypukły regularne wielościany, znany jako Platońskich stałych , cztery regularnie wielościanów gwiazdy , na wielościanów Keplera-Poinsot i pięć stałych związków regularnych wielościanów:

Bryły platońskie

Czworościan {3, 3}	Kostka {4, 3}	Oktaedron {3, 4}	Dwunastościan {5, 3}	Dwudziestościan {3, 5}
χ = 2	χ = 2	χ = 2	χ = 2	χ = 2

Wielościany Keplera-Poinsota

Mały dwunastościan gwiaździsty {5/2, 5}	Wielki dwunastościan {5, 5/2}	Wielki dwunastościan gwiaździsty {5/2, 3}	Wielki dwudziestościan {3, 5/2}
χ = -6	χ = -6	χ = 2	χ = 2

Zwykłe związki

Dwie czworościany 2 {3, 3}	Pięć czworościanów 5 {3, 3}	Dziesięć czworościanów 10 {3, 3}	Pięć kostek 5 {4, 3}	Pięć oktaedrów 5 {3, 4}
χ = 4	χ = 10	χ = 0	χ = −10	χ = 10

Charakterystyka

Równoważne właściwości

Właściwość posiadania podobnego układu ścian wokół każdego wierzchołka można zastąpić dowolnym z następujących równoważnych warunków w definicji:

• Wszystkie wierzchołki wypukłego wielościanu foremnego leżą na kuli .
• Wszystkie kąty dwuścienne wielościanu są równe
• Wszystkie figury wierzchołkowe wielościanu są wielokątami foremnymi .
• Wszystkie kąty bryłowe wielościanu są przystające.

Koncentryczne kule

Wypukły wielościan foremny ma wszystkie trzy powiązane ze sobą sfery (inne wielościany nie mają przynajmniej jednego rodzaju), które dzielą jego środek:

• Insphere , styczna do wszystkich twarzach.
• Międzykula lub kula środkowa styczna do wszystkich krawędzi.
• Circumsphere , styczna do wszystkich wierzchołków.

Symetria

Wielościany regularne są najbardziej symetryczne ze wszystkich wielościanów. Leżą one w zaledwie trzech grupach symetrii , których nazwa pochodzi od brył platońskich:

• Czworościenny
• Oktaedryczny (lub sześcienny)
• Dwudziestościan (lub dwunastościan)

Wszelkie kształty z symetrią dwudziestościenną lub oktaedryczną będą również zawierać symetrię czworościenną.

Charakterystyka Eulera

Pięć brył platońskich ma charakterystykę Eulera równą 2. Odzwierciedla to po prostu, że powierzchnia jest topologiczną 2-sferą, a więc jest również prawdą, na przykład, każdego wielościanu, który ma kształt gwiazdy w odniesieniu do jakiegoś punktu wewnętrznego.

Punkty wewnętrzne

Suma odległości od dowolnego punktu we wnętrzu wielościanu foremnego do boków jest niezależna od położenia punktu (jest to rozszerzenie twierdzenia Vivianiego ). Jednak odwrotność nie obowiązuje, nawet dla czworościanów .

Dualizm regularnych wielościanów

W podwójnej parze wielościanów wierzchołki jednego wielościanu odpowiadają ścianom drugiego i na odwrót.

Wielościany regularne pokazują tę dwoistość w następujący sposób:

• Czworościanu jest self-podwójny, to znaczy pary ze sobą.
• Sześcian i ośmiościan są podwójnym siebie.
• Dwudziestościan i dwunastościan są podwójnym siebie.
• Niewielki gwiezdny dwunastościan i wielki dwunastościan są podwójnym siebie.
• Wielki gwiezdny dwunastościan i wielki dwudziestościan to podwójny do siebie.

Symbol Schläfli dla liczby podwójnej jest po prostu oryginałem pisanym od tyłu, na przykład liczba dualna {5, 3} to {3, 5}.

Historia

Pre-historia

Kamienie wyrzeźbione w kształtach przypominających skupiska kulek lub gałek znaleziono w Szkocji i mogą mieć nawet 4000 lat. Niektóre z tych kamieni pokazują nie tylko symetrie pięciu brył platońskich, ale także niektóre relacje dualności między nimi (to znaczy, że środki ścian sześcianu dają wierzchołki ośmiościanu). Przykłady tych kamieni są wystawione w pokoju Johna Evansa Ashmolean Museum na Uniwersytecie Oksfordzkim . Dlaczego powstały te przedmioty lub jak ich twórcy zdobyli dla nich inspirację, pozostaje tajemnicą. Istnieje wątpliwość co do matematycznej interpretacji tych obiektów, ponieważ wiele z nich ma formy nieplatońskie i być może tylko jeden okazał się prawdziwym dwudziestościanem, w przeciwieństwie do reinterpretacji podwójnego dwudziestościanu, dwunastościanu.

Możliwe też, że Etruskowie wyprzedzili Greków w świadomości przynajmniej części wielościanów foremnych, o czym świadczy odkrycie pod Padwą (w północnych Włoszech ) pod koniec XIX wieku dwunastościanu wykonanego ze steatytu , a datowanego na więcej ponad 2500 lat (Lindemann, 1987).

Grecy

Najwcześniejsze znane pisemne wzmianki o regularnych wypukłych bryłach pochodzą z Grecji klasycznej. Kiedy te substancje stałe wszystko odkryte i przez kogo nie jest znana, ale Theaetetus (an ateński ) był pierwszym dać matematyczny opis wszystkich pięciu (Van der Waerden, 1954), (Euclid, książka XIII). HSM Coxeter (Coxeter, 1948, sekcja 1.9) kredyty Plato (400 pne) z konieczności wykonane modele nich, i wspomina, że jeden z wcześniejszych pitagorejczyków , Tymeusza z Locri , wykorzystane wszystkie pięć w korespondencji pomiędzy wielościanów i charakteru z wszechświat tak, jak był wtedy postrzegany – ta korespondencja jest utrwalona w dialogu Platona Timaeus . Odniesienie Euklidesa do Platona doprowadziło do ich wspólnego opisu jako brył platońskich .

Można scharakteryzować grecką definicję w następujący sposób:

• Wielokąt foremny to ( wypukła ) płaska figura o równych wszystkich krawędziach i równych wszystkich rogach.
• Wielościan foremny to bryła (wypukła) ze wszystkimi ścianami będącymi przystającymi wielokątami foremnymi, o tej samej liczbie ułożonej tak samo wokół każdego wierzchołka.

Ta definicja wyklucza na przykład ostrosłup kwadratowy (ponieważ wszystkie ściany są regularne, podstawa kwadratu nie jest przystająca do boków trójkąta) lub kształt utworzony przez połączenie ze sobą dwóch czworościanów (ponieważ wszystkie ściany tej trójkątnej bipiramidy byłyby trójkątami równobocznymi, to znaczy przystającymi i regularnymi, niektóre wierzchołki mają 3 trójkąty, a inne 4).

Ta koncepcja wielościanu foremnego pozostawałaby niekwestionowana przez prawie 2000 lat.

Wielościany regularne gwiazd

Regularne wielokąty gwiaździste, takie jak pentagram (pentagon gwiaździsty), były również znane starożytnym Grekom – pentagram był używany przez Pitagorejczyków jako ich sekretny znak, ale nie używali ich do budowy wielościanów. Dopiero na początku XVII wieku Johannes Kepler zdał sobie sprawę, że pentagramy mogą być używane jako twarze wielościanów regularnych . Niektóre z tych gwiezdnych wielościanów mogły zostać odkryte przez innych przed czasami Keplera, ale Kepler jako pierwszy uznał, że można je uznać za „regularne”, jeśli usunie się ograniczenie, że regularne wielościany są wypukłe. Dwieście lat później Louis Poinsot zezwolił również na figury wierzchołków gwiazdy (obwody wokół każdego rogu), umożliwiając mu odkrycie dwóch nowych wielościanów regularnych wraz z ponownym odkryciem Keplera. Te cztery są jedynymi regularnymi wielościanami gwiaździstymi i stały się znane jako wielościany Keplera-Poinsota . Dopiero w połowie XIX wieku, kilkadziesiąt lat po publikacji Poinsota, Cayley nadał im współczesne angielskie nazwy: (Keplera) mały gwiaździsty dwunastościan i wielki gwiaździsty dwunastościan oraz (Poinsota) wielki dwudziestościan i wielki dwunastościan .

Wielościany Keplera-Poinsota mogą być zbudowane z brył platońskich w procesie zwanym stelacją . Wzajemny proces stellacji nazywa się facetingiem (lub facetingiem ). Każda gwiazda jednego wielościanu jest podwójna lub odwrotna do pewnego fasetowania wielościanu podwójnego. Wielościany regularne gwiaździste można również uzyskać przez fasetowanie brył platońskich. Po raz pierwszy zrobił to Bertrand mniej więcej w tym samym czasie, w którym Cayley ich nazwał.

Pod koniec XIX wieku istniało zatem dziewięć wielościanów foremnych – pięć wypukłych i cztery gwiazdy.

Wielościany regularne w przyrodzie

Każda z brył platońskich występuje naturalnie w takiej czy innej formie.

Czworościan, sześcian i ośmiościan występują jako kryształy . W żadnym wypadku nie wyczerpują one liczby możliwych form kryształów (Smith, 1982, s.212), których jest 48. Wśród nich nie ma ani dwudziestościanu foremnego, ani dwunastościanu foremnego , ale kryształy mogą mieć kształt pirytoedru , co jest wizualnie prawie nie do odróżnienia od regularnego dwunastościanu. Prawdziwie dwudziestościenne kryształy mogą być tworzone z materiałów quasikrystalicznych, które są bardzo rzadkie w przyrodzie, ale można je wytwarzać w laboratorium.

Nowsze odkrycie dotyczy serii nowych typów cząsteczek węgla , znanych jako fulereny (patrz Curl, 1991). Chociaż C ₆₀ , najłatwiejszy do produkcji fuleren, wygląda mniej więcej kuliście, przypuszcza się, że niektóre większe odmiany (takie jak C ₂₄₀ , C ₄₈₀ i C ₉₆₀ ) przybierają postać lekko zaokrąglonych ikosaedrów o średnicy kilku nanometrów.

Wielościany pojawiają się również w biologii. Na początku XX wieku Ernst Haeckel opisał szereg gatunków Radiolaria , których szkielety mają kształt różnych wielościanów foremnych (Haeckel, 1904). Przykłady obejmują Circoporus octahedrus , Circogonia icosahedra , Lithocubus geometricus i Circorrhegma dodecahedra ; kształty tych stworzeń są wskazane przez ich nazwy. Zewnętrzne otoczki białkowe wielu wirusów tworzą wielościany regularne. Na przykład wirus HIV jest zamknięty w regularnym dwudziestościanie.

W starożytności pitagorejczycy wierzyli, że istnieje harmonia między regularnymi wielościanami a orbitami planet . W XVII wieku Johannes Kepler badał dane o ruchu planet zebrane przez Tycho Brahe i przez dekadę próbował ustalić ideał pitagorejski, znajdując dopasowanie między rozmiarami wielościanów a rozmiarami orbit planet. Jego poszukiwania nie powiodły się w pierwotnym celu, ale z tych badań wyszły Keplerowskie odkrycia brył Keplera jako regularnych politopów, uświadomienie sobie, że orbity planet nie są okręgami, oraz prawa ruchu planet, z których jest teraz znany. W czasach Keplera znanych było tylko pięć planet (nie licząc Ziemi), co ładnie odpowiadało liczbie brył platońskich. Praca Keplera i odkrycie od tamtego czasu Urana i Neptuna unieważniły ideę pitagorejską.

Mniej więcej w tym samym czasie co pitagorejczycy, Platon opisał teorię materii, w której każdy z pięciu elementów (ziemia, powietrze, ogień, woda i duch) składał się z maleńkich kopii jednej z pięciu regularnych brył. Z mieszanki tych wielościanów zbudowano materię, przy czym każda substancja ma różne proporcje w mieszance. Dwa tysiące lat później teoria atomowa Daltona wykazała, że ​​idea ta jest właściwa, choć nie ma bezpośredniego związku z regularnymi ciałami stałymi.

Dalsze uogólnienia

W XX wieku nastąpił szereg uogólnień idei wielościanu foremnego, co doprowadziło do powstania kilku nowych klas.

Regularne pochylenie apeirohedra

W pierwszych dekadach Coxeter i Petrie dopuścili „siodłane” wierzchołki z naprzemiennymi grzbietami i dolinami, umożliwiając im skonstruowanie trzech nieskończonych pofałdowanych powierzchni, które nazwali regularnymi wielościanami skośnymi . Coxeter zaoferował zmodyfikowany symbol Schläfliego {l,m|n} dla tych figur, gdzie {l,m} implikuje figurę wierzchołkową , gdzie m regularnych l- gonów wokół wierzchołka. Gdy n definiuje N -gonal otwory . Ich figury wierzchołkowe są regularnymi wielokątami skośnymi , wierzchołkami zygzakowatymi między dwiema płaszczyznami.

Nieskończony regularny wielościan skośny w przestrzeni 3 (częściowo narysowany)
{4,6|4}	{6,4|4}	{6,6|3}

Wielościany regularne skośne

Skończone regularne wielościany skośne istnieją w 4-przestrzeni. Te skończone regularne wielościany skośne w 4-przestrzeni mogą być postrzegane jako podzbiór ścian jednolitych 4-politopów . Mają płaskie powierzchnie wielokątów foremnych , ale figury wierzchołków wielokątów foremnych skośnych .

Dwa podwójne rozwiązania są związane z 5-ogniwami , dwa podwójne rozwiązania są związane z 24-ogniwami , a nieskończony zestaw samopodwójnych duopryzmów generuje regularne skośne wielościany jako {4, 4 | n}. W nieskończonej granicy zbliżają się one do duocylindra i wyglądają jak torus w swoich rzutach stereograficznych w 3-przestrzeń.

Wielościany skończone regularne skośne w 4-przestrzeni

Ortogonalne Coxeter płaskie występy				Projekcja stereograficzna
4		F 4
{4, 6 | 3}	{6, 4 | 3}	{4, 8 | 3}	{8, 4 | 3}	{4, 4 | n}
30 {4} twarze 60 krawędzi 20 wierzchołków	20 {6} twarzy 60 krawędzi 30 wierzchołków	288 {4} twarze 576 krawędzi 144 wierzchołki	144 {8} twarzy 576 krawędzi 288 wierzchołków	n 2 {4} ściany 2 n 2 krawędzie n 2 wierzchołki

Wielościany regularne w przestrzeniach nieeuklidesowych i innych

Badania nad przestrzeniami nieeuklidesowymi ( hiperbolicznymi i eliptycznymi ) oraz innymi przestrzeniami, takimi jak przestrzenie złożone , odkryte w poprzednim stuleciu, doprowadziły do ​​odkrycia nowych wielościanów, takich jak wielościany złożone, które mogły w tych przestrzeniach przyjmować tylko regularną formę geometryczną.

Wielościany regularne w przestrzeni hiperbolicznej

W H ³ hiperbolicznej przestrzeni , parazwartą regularne plastry miodu mają euklidesowe Dachówka aspekty i postacie wierzchołków , które zachowują się jak skończony wielościanów. Takie płytki mają wadę kątową, którą można zamknąć poprzez zginanie w jedną lub drugą stronę. Jeśli kafelkowanie jest odpowiednio wyskalowane, zamknie się jako asymptotyczny limit w jednym idealnym punkcie . Te kafelki euklidesowe są wpisane w horosferę, tak jak wielościany są wpisane w sferę (która zawiera zero punktów idealnych). Sekwencja rozszerza się, gdy same płytki hiperboliczne są używane jako fasety niezwartych teselacji hiperbolicznych, jak w siedmiokątnym kafelkowym plastrze miodu {7,3,3}; są one wpisane w równoodległą powierzchnię (2- hipercykl ), która ma dwa idealne punkty.

Regularne kafelki rzeczywistej płaszczyzny rzutowej

Inną grupę wielościanów foremnych stanowią kafelki rzeczywistej płaszczyzny rzutowej . Należą do nich hemi-sześcian , hemi-oktaedr , hemi-dodecahedron i hemi-cosahedron . Są (globalnie) wielościanami projekcyjnymi i są projekcyjnymi odpowiednikami brył platońskich . Czworościan nie ma odpowiednika rzutowego, ponieważ nie ma par równoległych ścian, które można zidentyfikować, tak jak pozostałe cztery bryły platońskie.

Półsześcian {4,3}

Półoktaedr {3,4}

Półdwunastościan {3,5}

Półścian {5,3}

Występują one jako pary podwójne w taki sam sposób, jak oryginalne bryły platońskie. Wszystkie ich cechy Eulera to 1.

Abstrakcyjne wielościany regularne

Do tej pory wielościany były dobrze rozumiane jako trójwymiarowe przykłady bardziej ogólnych wielościanów w dowolnej liczbie wymiarów. W drugiej połowie wieku rozwinęły się abstrakcyjne idee algebraiczne, takie jak kombinatoryka wielościenna , których kulminacją była idea abstrakcyjnego wielotopu jako częściowo uporządkowanego zbioru (posetu) elementów. Elementami abstrakcyjnego wielościanu są jego ciało (element maksymalny), jego ściany, krawędzie, wierzchołki oraz wielościan zerowy lub zbiór pusty. Te abstrakcyjne elementy można odwzorować w zwykłej przestrzeni lub zrealizować jako figury geometryczne. Niektóre abstrakcyjne wielościany mają dobrze ukształtowane lub wierne realizacje, inne nie. Flaga jest połączony zestaw elementów każdego wymiaru - dla bryły, która jest ciałem, twarz, krawędź twarzy, wierzchołek ostrza i zerowy Polytope. Mówi się, że abstrakcyjny wielotop jest regularny, jeśli jego kombinatoryczne symetrie są przechodnie na jego flagach – to znaczy, że każda flaga może być odwzorowana na dowolną inną pod symetrią wielościanu. Abstrakcyjne politopy regularne pozostają aktywnym obszarem badań.

Pięć takich abstrakcyjnych wielościanów regularnych, których nie można wiernie zrealizować, zidentyfikował HSM Coxeter w jego książce Regular Polytopes (1977) i ponownie JM Wills w pracy „The kombinatorycznie regularne wielościany o indeksie 2” (1987). Wszystkie pięć mają symetrię C ₂ × S _5, ale można je zrealizować tylko z połową symetrii, to jest C ₂ × A ₅ lub symetrią dwudziestościenną. Wszystkie są topologicznie równoważne toroidom . Ich konstrukcja, poprzez rozmieszczenie n ścian wokół każdego wierzchołka, może być powtarzana w nieskończoność jako kafelki płaszczyzny hiperbolicznej . Na poniższych diagramach hiperboliczne obrazy kafelkowe mają kolory odpowiadające kolorom obrazów wielościanów.

Wielościan	Przyśrodkowy rombowy triacontahedron	Dwunastodwunastościan	Przyśrodkowy triambic dwudziestościan	Dwunastokątny dwuspadowy dwunastościan	Odkopany dwunastościan
Rodzaj	Podwójny {5,4} 6	{5,4} 6	Dual {5,6} 4	{5,6} 4	{6,6} 6
( v , e , f )	(24,60,30)	(30,60,24)	(24,60,20)	(20,60,24)	(20,60,20)
Figura wierzchołka	{5}, {5/2}	(5,5/2) 2	{5}, {5/2}	(5,5/3) 3
Twarze	30 rombów	12 pięciokątów 12 pentagramów	20 sześciokątów	12 pięciokątów 12 pentagramów	20 heksagramów
Dekarstwo	{4, 5}	{5, 4}	{6, 5}	{5, 6}	{6, 6}
χ	-6	-6	−16	−16	-20

Petrie dual

Petrie podwójny regularnego wielościanu jest regularne mapa którego wierzchołki i krawędzie odpowiadają wierzchołkach i krawędziach pierwotnego wielościanu, a których twarze są zbiorem skośnych Wielokąt Petriego .

Zwykłe petals

Nazwa	Czworościan Petrialny	Kostka Petrali	Ośmiościan Petrialny	Petrial dwunastościan	dwudziestościan Petrialny
Symbol	{3,3} π	{4,3} π	{3,4} π	{5,3} π	{3,5} π
( v , e , f ), χ	(4,6,3), χ = 1	(8,12,4), χ = 0	(6,12,4), χ = −2	(20,30,6), χ = −4	(12,30,6), χ = −12
Twarze	3 skośne kwadraty	4 skośne sześciokąty		6 skośnych dziesięciokątów
Obraz
Animacja
Powiązane dane	{4,3} 3 = {4,3}/2 = {4,3} (2,0)	{6,3} 3 = {6,3} (2,0)	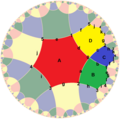{6,4} 3 = {6,4} (4,0)	{10,3} 5	{10,5} 3

Wielościany sferyczne

Zwykłe dziewięć wielościanów regularnych można również przedstawić jako kafelki sferyczne (kafelki kuli ):

Czworościan {3,3}

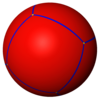Kostka {4,3}

ośmiościan {3,4}

Dwunastościan {5,3}

Dwudziestościan {3,5}

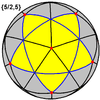Mały dwunastościan gwiaździsty {5/2,5}

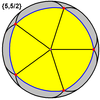wielki dwunastościan {5,5/2}

Wielki dwunastościan gwiaździsty {5/2,3}

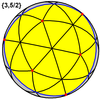Wielki dwudziestościan {3,5/2}

Regularne wielościany, które mogą istnieć tylko jako wielościany sferyczne

Dla wielościanu foremnego, którego symbolem Schläfliego jest { m ,  n }, liczbę ścian wielokątnych można znaleźć przez:

${\ Displaystyle N_ {2} = {\ Frac {4n} {2m + 2n-min}}}$

W Platońskie substancji stałych znane starożytności są tylko całkowitą rozwiązania dla m ≥ 3 i n ≥ 3. ograniczenie m ≥ 3 wymusza że wieloboczne powierzchnie muszą mieć co najmniej z trzech stron.

Rozważając wielościany jako sferyczne płytki , to ograniczenie można złagodzić, ponieważ dwukąty (2-kątne) mogą być reprezentowane jako sferyczne księżyce o niezerowej powierzchni . Dopuszczenie m = 2 dopuszcza nową nieskończoną klasę wielościanów regularnych, którymi są hozoedry . Na powierzchni sferycznej wielościan foremny {2,  n } jest przedstawiony jako n przylegających do siebie księżyców o kątach wewnętrznych 2 π / n . Wszystkie te księżyce mają dwa wspólne wierzchołki.

Dwuścian foremny , { n , 2} (2-ścian) w trójwymiarowej przestrzeni euklidesowej można uznać za zdegenerowany graniastosłup składający się z dwóch (planarnych) n- bocznych wielokątów połączonych "tyłem do siebie", tak że wynikowy obiekt nie ma głębokości, analogicznie do tego, jak można skonstruować dwukąt z dwoma odcinkami linii . Jednak jako kafelek kulisty , dwuścian może istnieć w postaci niezdegenerowanej, z dwiema n- stronnymi ścianami pokrywającymi sferę, przy czym każda ściana jest półkulą i wierzchołkami wokół wielkiego koła . Jest regularny, jeśli wierzchołki są równomiernie rozmieszczone.

Digonal dwuścian {2,2}	Dwuścian trójkątny {3,2}	Dwuścian kwadratowy {4,2}	Dwuścian pięciokątny {5,2}	Sześciokątny dwuścian {6,2}	...	{ n ,2}
Dwuboczny dwuścian {2,2}	Trójścian trójkątny {2,3}	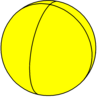Trójkąt kwadratowy {2,4}	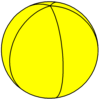Pięciokątny wielościan {2,5}	Sześciościan sześciokątny {2,6}	...	{2, n }

Dwuścian {2, n } jest podwójny do dwuścianu { n ,2}. Zwróć uwagę, że gdy n = 2, otrzymujemy wielościan {2,2}, który jest zarówno wielościanem, jak i dwuścianem. Wszystkie mają charakterystykę Eulera 2.

Zobacz też

• Wielościan kwaziregularny
• Wielościan półregularny
• Jednolity wielościan
• Zwykły polytope

Bibliografia

• Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences , 46 , s. 79–82.
• Haeckel, E. (1904). Kunstformen der Natur . Dostępne jako Haeckel, E. Formy sztuki w przyrodzie , Prestel USA (1998), ISBN  3-7913-1990-6 lub online pod adresem http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/ natur.html
• Smith, JV (1982). Krystalografia geometryczna i strukturalna . John Wiley i Synowie.
• Sommerville, DMY (1930). Wprowadzenie do geometrii n wymiarów. EP Dutton, Nowy Jork. (wydanie z wydawnictwa Dover, 1958). Rozdział X: Regularne Polytopes.
• Coxeter, HSM ; Regularne Polytopes (wydanie trzecie). Dover Publications Inc. ISBN  0-486-61480-8

Zewnętrzne linki

• Weisstein, Eric W. „Regularny wielościan” . MatematykaŚwiat .