Dwunastościan rombowy - Rhombic dodecahedron
| Dwunastościan rombowy | |
|---|---|
 (Kliknij tutaj, aby zobaczyć model obrotowy) |
|
| Rodzaj | kataloński stały |
| Schemat Coxetera |
   
|
| notacja Conway | jC |
| Typ twarzy | V3.4.3.4 romb |
| Twarze | 12 |
| Krawędzie | 24 |
| Wierzchołki | 14 |
| Wierzchołki według typu | 8{3}+6{4} |
| Grupa symetrii | O h , B 3 , [4,3], (*432) |
| Grupa rotacyjna | O, [4,3] + , (432) |
| Kąt dwuścienny | 120° |
| Nieruchomości | wypukły, twarzowo przechodni izohedral , izotoksal , równoległościan |
 Sześcian ( podwójny wielościan ) |
 Internet |
W geometrii , że dwunastościan rombowy jest A wypukły wielościan z 12 przystających rombowe twarze . Ma 24 krawędzie i 14 wierzchołków 2 typów. Jest to kataloński stałe i podwójny wielościan z sześcio-ośmiościan .
Nieruchomości
Dwunastościan rombowy jest zonohedronem . Jej wielościenny dual to sześcian sześcienny . Długość przekątnej ściany długiej jest dokładnie √ 2 razy większa od długości przekątnej ściany krótkiej; w ten sposób kąty ostre na każdej powierzchni mierzą arccos (1/3) lub około 70,53 °.
Będąc dualem wielościanu Archimedesa , dwunastościan rombowy jest przechodni twarzowo , co oznacza, że grupa symetrii bryły działa przechodnie na jej zestaw ścian. W elementarnym ujęciu oznacza to, że dla dowolnych dwóch ścian A i B następuje obrót lub odbicie bryły, które pozostawia ją w tym samym obszarze przestrzeni podczas przesuwania ściany A do ściany B.
Dwunastościan rombowy może być postrzegany jako wypukły kadłub połączenia wierzchołków sześcianu i ośmiościanu. 6 wierzchołków, w których spotykają się 4 romby, odpowiada wierzchołkom ośmiościanu , a 8 wierzchołków, w których spotykają się 3 romby, odpowiada wierzchołkom sześcianu .
Rombowego dwunastościanu jest jednym z dziewięciu krawędzi przechodni wypukłych wielościanów, inne to pięć platońskie ciał stałych , tym sześcio-ośmiościan The icosidodecahedron i trzydziestościan rombowy .
Dwunastościan rombowy może być użyty do teselacji trójwymiarowej przestrzeni: może być ułożony w stos, aby wypełnić przestrzeń, podobnie jak sześciokąty wypełniają płaszczyznę.
Ten wielościan w teselacji wypełniającej przestrzeń może być postrzegany jako teselacja Voronoi sieci sześciennej skoncentrowanej na ścianie . Jest to strefa Brillouina kryształów sześciennych (BCC) skupionych wokół ciała. Niektóre minerały, takie jak granat, tworzą rombowy, dwunastościenny pokrój kryształów . Jak zauważył Johannes Kepler w swojej książce z 1611 r. o płatkach śniegu ( Strena seu de Nive Sexangula ), pszczoły miodne wykorzystują geometrię dwunastościanu rombowego do tworzenia plastrów miodu z teselacji komórek, z których każda jest sześciokątnym pryzmatem zakończonym połową dwunastościanu rombowego. Dwunastościan rombowy pojawia się również w komórkach elementarnych diamentu i diamentoidów . W takich przypadkach nie ma czterech wierzchołków (naprzemiennych potrójnych), ale wiązania chemiczne leżą na pozostałych krawędziach.
Wykres dwunastościanu rombowego jest niehamiltonianem .
Dwunastościan rombowy może być rozcięta na 4 rozwarty trójkątny trapezohedra wokół jego środka. Te romboedry są komórkami trójkątnego trapezoedrycznego plastra miodu . Analogia: Sześciokąt foremny można rozciąć na 3 romby wokół jego środka. Te romby to kafelki rombów .
W zbiorach Luwru znajduje się kostka w kształcie dwunastościanu rombowego, pochodząca z ptolemejskiego Egiptu . Twarze są wyryte greckimi literami reprezentującymi liczby od 1 do 12: Α Β Γ Δ Ε Ζ Ϛ Η Θ Ι ΙΑ ΙΒ. Funkcja matrycy nie jest znana.
Dwunastościan rombowy
Sześciokąt rozcięty rombowo
Granat kryształ
Ta animacja przedstawia konstrukcję dwunastościanu rombowego z sześcianu, poprzez odwrócenie piramid w środkowej ściance sześcianu.
Wymiary
Oznaczając przez o długości krawędzi dwunastościanu rombowego,
- promień jego Kula wpisana ( styczna do każdej twarzach dwunastościan rombowy za) jest
- promień jego kuli środkowej wynosi
- promień kuli przechodzącej przez sześć wierzchołków rzędu 4, ale nie przez osiem wierzchołków rzędu 3, jest
- promień kuli przechodzącej przez wierzchołki ósmego rzędu 3 jest dokładnie równy długości boków
Powierzchnia i objętość
Pole powierzchni A i objętość V dwunastościanu rombowego o długości krawędzi a wynoszą:
Rzuty prostopadłe
Rombowy dwunastościan cztery specjalne występy prostokątne wzdłuż jej osi symetrii , na środku powierzchni czołowej, krawędzi, oraz dwa rodzaje wierzchołków, trzykrotnie, czterokrotnie. Ostatnie dwa odpowiadają samolotom B 2 i A 2 Coxeter .
Symetria projekcyjna |
[4] | [6] | [2] | [2] |
|---|---|---|---|---|
Dwunastościan rombowy |
|
|
|
|
| Sześcian (podwójny) |
|
|
|
|
współrzędne kartezjańskie
 Odmiany pirytoedru między sześcianem a dwunastościanem rombowym |
 Rozbudowa dwunastościanu rombowego |
Osiem wierzchołków, w których trzy twarze spotykają się pod kątem rozwartym, ma współrzędne kartezjańskie :
- (±1, ±1, ±1)
Współrzędne sześciu wierzchołków, w których cztery ściany spotykają się pod ich ostrymi kątami, to:
- (±2, 0, 0), (0, ±2, 0) i (0, 0, ±2)
Dwunastościan rombowy może być postrzegany jako zdegenerowany przypadek graniczny pirytoedru z permutacją współrzędnych (±1, ±1, ±1) i (0, 1 + h , 1 − h 2 ) z parametrem h = 1.
Topologicznie równoważne formy
równoległościan
Dwunastościan rombowy jest parallelohedron , A , wypełniającymi przestrzeń wielościan , dodecahedrille , jako podwójny do tetroctahedrille lub pół sześciennej strukturze plastra miodu , i opisany przez dwóch schematów Coxeter :
oraz 
. Dzięki symetrii D 3d można ją postrzegać jako wydłużony trójkątny trapezohedron .
 Dwunastościan rombowy może teselować przestrzeń przez translacyjne kopie samego siebie , podobnie jak dwunastościan rombowy gwiaździsty . |
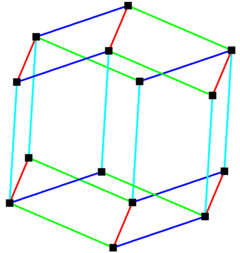 Rombowy dwunastościan może być wykonana z 4 zestawów 6 równoległych krawędziach. |
Dwuścienny rombowy dwunastościan
Inne konstrukcje symetrii dwunastościanu rombowego również wypełniają przestrzeń i jako równoległościany są podobne do odmian ośmiościanu ściętego wypełniającego przestrzeń .
Na przykład, z 4 kwadratowymi ścianami i 60-stopniowymi rombowymi ścianami i dwuścienną symetrią D 4h , rząd 16. Można go zobaczyć jako prostopadłościan z kwadratowymi piramidami powiększonymi na górze i na dole.
|
 Internet |
Współrzędne
|
Dwunastościan Bilińskiego
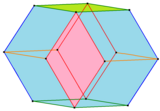 Dwunastościan Bilińskiego o krawędziach i licach pokolorowanych według ich symetrii. |
 Dwunastościan Bilińskiego pokolorowany równoległymi krawędziami |
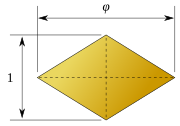
W 1960 roku Stanko Biliński odkrył drugi dwunastościan rombowy z 12 przystającymi ścianami rombowymi, dwunastościan Biliński . Ma tę samą topologię, ale inną geometrię. Twarze rombowe w tej formie mają złoty podział .
| Pierwsza forma | Druga forma |
|---|---|
|
|
|
| √ 2 : 1 | √ 5 + 1/2:1 |
Dwunastościan deltoidalny
.jpg)
Inna topologicznie równoważna odmiana, czasami nazywana dwunastościanem deltoidalnym lub dwunastościanem trapezoidalnym , jest izohedralna z czworościennym porządkiem symetrii 24, zniekształcająca ściany rombowe w latawce (naramienne). Ma 8 wierzchołków regulowanych do środka lub na zewnątrz w naprzemiennych zestawach po 4, z ograniczeniem w czworościennej obwiedni. Wariacje można sparametryzować za pomocą ( a , b ), gdzie b i a zależą od siebie w taki sposób, że czworościan wyznaczony przez cztery wierzchołki ściany ma objętość zerową, czyli jest ścianą płaską. (1,1) jest rozwiązaniem rombowym. W miarę zbliżania się ( a )1/2, ( b ) zbliża się do nieskończoności. Zawsze trzyma1/a + 1/b = 2, gdzie a,b > 1/2.
- (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)
- ( a , a , a ), (− a , − a , a ), (− a , a , − a ), ( a , − a , − a )
- (− b , − b , − b ), (− b , b , b ), ( b , − b , b ), ( b , b , − b )
| (1,1) | (7/8,7/6) | (3/4,3/2) | (2/3,2) | (5/8,5/2) | (9/16,9/2) |
|---|---|---|---|---|---|
|
|
|
|
|
|
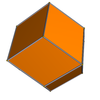
Powiązane wielościany
| Jednolite wielościany ośmiościenne | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symetria : [4,3], (*432) | [4,3] + (432) |
[1 + ,4,3] = [3,3] (*332) |
[3 + ,4] (3*2) |
|||||||
| {4,3} | t{4,3} |
r{4,3} r{3 1,1 } |
t{3,4} t{3 1,1 } |
{3,4} {3 1,1 } |
rr{4,3} s 2 {3,4} |
tr{4,3} | sr{4,3} |
godz.{4,3} {3,3} |
h 2 {4,3} t{3,3} |
s{3,4} s{3 1,1 } |
|
|
|
|
|
|
|
|
|
||
 = 
|
=
|
=
|
|
 = lub 
|
= lub
|
=
|
||||
|
|
 
|
 
|
 
|
 
|
|
|
 
|
 
|
 
|
| Duals do jednolitych wielościanów | ||||||||||
| V4 3 | V3.8 2 | V(3.4) 2 | V4.6 2 | V3 4 | V3.4 3 | Wersja 4.6.8 | V3 4 0,4 | V3 3 | V3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Po rzucie na kulę (patrz po prawej) można zauważyć, że krawędzie tworzą krawędzie dwóch czworościanów ułożonych w swoich podwójnych pozycjach (stella octagula). Tendencja ta jest kontynuowana w przypadku deltoidalnego ikozytościanu i deltoidalnego sześciościanu dla podwójnych par innych regularnych wielościanów (obok trójkątnej dwupiramidy, jeśli wziąć pod uwagę niewłaściwe układanie płytek ), nadając temu kształtowi alternatywną systematyczną nazwę dwunastościanu naramiennego .
| Symetria * n 32 [n,3] |
Kulisty | Euklidesa. | Kompaktowa hiperb. | Parako. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
|
| Rysunek Konfig. |
 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
Ten wielościan jest częścią ciągu wielościanów rombowych i kafelków o symetrii grupy Coxetera [ n , 3] . Sześcian może być postrzegany jako rombowy sześcian, gdzie romb to kwadraty.
| Mutacje symetrii podwójnych płytek quasiregularnych : V(3.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | Kulisty | Euklidesa | Hiperboliczny | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Dekarstwo |
|
|
|
|
|
|
|
||||
| Konf. | V(3.3) 2 | V(3.4) 2 | V(3.5) 2 | V(3.6) 2 | V(3.7) 2 | V(3.8) 2 | V(3.∞) 2 | ||||
| * n 42 mutacje symetrii quasiregularnych podwójnych płytek: V (4.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symetria *4n2 [n,4] |
Kulisty | Euklidesa | Kompaktowy hiperboliczny | Parakompaktowy | Niekompaktowy | ||||||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[iπ/λ,4] |
||||
| Dachówka Konf. |
V4.3.4.3 |
 V4.4.4.4 |
 V4.5.4.5 |
 V4.6.4.6 |
 V4.7.4.7 |
 V4.8.4.8 |
 V4.∞.4.∞ |
V4.∞.4.∞ | |||
Podobnie odnosi się do nieskończonej serii płytek o konfiguracjach ścian V3.2 n .3.2 n , pierwsza w płaszczyźnie euklidesowej, a reszta w płaszczyźnie hiperbolicznej.
 V3.4.3.4 (narysowany jako siatka ) |
 V3.6.3.6 Dachówka z płaszczyzny euklidesowej Dachówka rombowa |
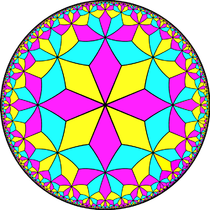 V3.8.3.8 Hiperboliczne kafelki płaszczyzny (narysowane w modelu dysku Poincaré ) |
Stellations
Podobnie jak wiele wielościanów wypukłych, dwunastościan rombowy może być stelated przez wydłużenie ścian lub krawędzi, aż spotkają się, tworząc nowy wielościan. Kilka takich stelacji zostało opisanych przez Dormana Luke'a.
Pierwsza gwiazda, często nazywana po prostu gwiaździstym dwunastościanem rombowym , jest dobrze znana. Może być postrzegany jako dwunastościan rombowy z każdą ścianą powiększoną poprzez przymocowanie do niej piramidy rombowej, o takiej wysokości piramidy, że boki leżą w płaszczyznach ścian sąsiednich ścian:
Pierwsza gwiazda dwunastościanu rombowego
Model 3D rozkładu na 12 piramid i 4 półsześciany
Łukasz opisuje jeszcze cztery gwiazdy: drugą i trzecią (rozszerzające się na zewnątrz), jedną utworzoną przez usunięcie drugiej z trzeciej, a drugą przez dodanie pierwotnego dwunastościanu rombowego z powrotem do poprzedniego.
| druga | Trzeci |
|---|---|
 Dwunastościan rombowy gwiaździsty |
 Świetny rozgwieżdżony dwunastościan rombowy |
Powiązane politopy
Dwunastościan rombowy tworzy kadłub rzutu wierzchołkowego tesseractu na trzy wymiary. Istnieją dokładnie dwa sposoby rozłożenia dwunastościanu rombowego na cztery przystające romboedry , dające osiem możliwych rombohedr jako rzuty teseraktów o 8 komórkach sześciennych. Jeden zestaw wektorów rzutowych to: u =(1,1,-1,-1), v =(-1,1,-1,1), w =(1,-1,-1,1).
Dwunastościan rombowy tworzy maksymalny przekrój 24 komórek , a także tworzy kadłub jego pierwszego wierzchołka w projekcji równoległej w trzech wymiarach. Dwunastościan rombowy można rozłożyć na sześć przystających (ale nieregularnych) dwupiramid kwadratowych spotykających się w jednym wierzchołku w środku; tworzą one obrazy sześciu par komórek oktaedrycznych 24 komórek. Pozostałe 12 komórek oktaedrycznych rzutuje na ściany dwunastościanu rombowego. Nieregularność tych obrazów wynika z zniekształceń projekcyjnych; fasety 24-komórki są regularnymi oktaedrami w 4-przestrzeni.
Ten rozkład daje interesującą metodę konstrukcji dwunastościanu rombowego: pociąć sześcian na sześć przystających ostrosłupów kwadratowych i przymocować je do ścian drugiego sześcianu. Trójkątne ściany każdej pary sąsiednich piramid leżą na tej samej płaszczyźnie, a więc łączą się w romb. 24 komórkę można również skonstruować w analogiczny sposób przy użyciu dwóch teseraktów .
Praktyczne zastosowanie
W układzie koła reakcyjnego statku kosmicznego powszechnie stosuje się konfigurację czworościenną czterech kół. W przypadku kół, które działają jednakowo (z punktu widzenia szczytowego momentu obrotowego i maksymalnego momentu pędu) w obu kierunkach obrotu i na wszystkich czterech kołach, maksymalny moment obrotowy i maksymalne obwiednie pędu dla 3-osiowego systemu kontroli położenia (z uwzględnieniem wyidealizowanych siłowników) są podane przez rzutowanie tesserakt stanowiących ograniczenia momentu każde koło lub pędu do 3D miejsca za pośrednictwem 3 x 4 matrycy osi koła; powstały wielościan 3D jest dwunastościanem rombowym. Taki układ kół reakcyjnych nie jest jedyną możliwą konfiguracją (prostszy układ składa się z trzech kół zamontowanych tak, aby obracały się wokół osi prostopadłych), ale jest korzystny w zapewnieniu nadmiarowości w celu złagodzenia awarii jednego z czterech kół (przy pogorszeniu ogólnej wydajności dostępne z pozostałych trzech aktywnych kół) i zapewniając bardziej wypukłą obwiednię niż sześcian, co prowadzi do mniejszej zależności zwinności w kierunku osi (z punktu widzenia siłownika/rośliny). Właściwości masy statku kosmicznego wpływają na ogólny pęd i zwinność systemu, więc zmniejszona zmienność granicy obwiedni niekoniecznie prowadzi do zwiększenia jednorodności w preferowanych odchyleniach osi (to znaczy, nawet przy idealnie rozłożonym limicie wydajności w podsystemie siłownika, preferowane osie obrotu niekoniecznie są arbitralne na poziomie systemu).
Zobacz też
- Dwunastościan
- rombowy triacontahedron
- Dwunastościan rombowy ścięty
- 24-ogniwowy analog 4D rombowego dwunastościanu
- Systemy konstrukcyjne Archimede
- W pełni ścięty dwunastościan rombowy
Bibliografia
Dalsza lektura
- Williams, Robert (1979). Geometryczne podstawy struktury naturalnej: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X. (Rozdział 3-9)
- Wenninger, Magnus (1983). Modele podwójne . Wydawnictwo Uniwersytetu Cambridge. doi : 10.1017/CBO9780511569371 . Numer ISBN 978-0-521-54325-5. MR 0730208 . (Trzynaście półregularnych wielościanów wypukłych i ich pary podwójne, str. 19, dwunastościan rombowy)
- Symetrie rzeczy 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (rozdział 21, Nazywanie wielościanów Archimedesa i katalońskiego i kafelki, s. 285, dwunastościan rombowy)
Zewnętrzne linki
- Eric W. Weisstein , dwunastościan rombowy ( bryła katalońska ) w MathWorld .
- Wielościany wirtualnej rzeczywistości – encyklopedia wielościanów
Modele komputerowe
- Odnoszące się trzydziestościan rombowy i rombowego dwunastościanu , rombowego dwunastościanu 5 Związek i rombowe dwunastościanu 5-związek Sandor Kabai, The demonstracji Wolfram projektu .
Projekty papierowe
- Kalendarz dwunastościan rombowy – zrób dwunastościan rombowy kalendarza bez kleju
- Kolejny rombowy kalendarz dwunastościanowy – wykonany przez splatanie pasków papieru
Praktyczne zastosowania
- Archimede Institute Przykłady rzeczywistych projektów budownictwa mieszkaniowego wykorzystujących tę geometrię