Funkcja suriektywna - Surjective function

W matematyce , A suriekcją funkcja (znany również jako surjection albo na funkcji ) to funkcja $f$ , który odwzorowuje elementu $x$ do każdego elementu $Y$ ; to znaczy, dla każdego $y$ istnieje $x$ takie, że $f (x) = y$ . Innymi słowy, każdy element funkcji za codomain jest obraz z co najmniej jednego elementu swojej domenie . Nie jest wymagane, aby $x$ było unikatowe ; funkcja $f$ może mapować jeden lub więcej elementów $X$ na ten sam element $Y$ .

Nie-różnowartościową suriekcją funkcji (surjection, nie bijection)
Różnowartościową suriekcją funkcji (bijection)
Injective non-surjective funkcja (wstrzyknięcie, a nie bijekcja)
Non-injective non-surjective funkcja (również nie bijection)

Termin suriektyw i pokrewne terminy — injective i bijjective — zostały wprowadzone przez Nicolasa Bourbakiego , grupę głównie francuskich matematyków XX wieku, którzy pod tym pseudonimem napisali od 1935 roku serię książek prezentujących wykład o nowoczesnej zaawansowanej matematyce. słowo sur oznacza ponad lub powyżej i odnosi się do faktu, że obraz dziedziny funkcji suriektywnej całkowicie pokrywa jej domenę.

Każda funkcja wywołuje odrzucenie, ograniczając swoją kodziedzinę do obrazu swojej domeny. Każda funkcja surjektywna ma prawo odwrotność , a każda funkcja z prawo odwrotnością jest z konieczności sujekcją. Skład funkcji suriekcją jest zawsze suriekcją. Każdą funkcję można rozłożyć na iniekcję i iniekcję.

Definicja

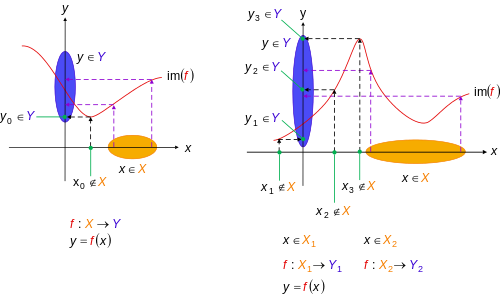
Funkcja surjektywna to funkcja, której obraz jest równy jej przeciwdziedzinie . Równoważnie funkcja z domeną i przeciwdziedziną jest surjektywna, jeśli dla każdego w istnieje co najmniej jeden w z . Surjekcje są czasami oznaczane dwugrotową strzałką w prawo ( U+ 21A0 ↠ DWUGŁOWOWA STRZAŁKA W PRAWO ), jak w . $f$ ${\ Displaystyle X}$ ${\ Displaystyle Y}$ $y$ ${\ Displaystyle Y}$ $x$ ${\ Displaystyle X}$ ${\ Displaystyle f (x) = y}$ $f\colon X\twoheadrightarrow Y$

Symbolicznie,

Jeśli , to jest surjektywna, jeśli

f\okrężnica X\rightarrow Y

f

{\ Displaystyle \ forall y \ w Y \, \ istnieje x \ w X \; \; f (x) = y}

.

Przykłady

Funkcja niesuriektywna od domeny X do przeciwdomeny Y . Mniejszy żółty owal wewnątrz Y to obraz (zwany także zakresem ) f . Ta funkcja nie jest surjektywna, ponieważ obraz nie wypełnia całej przeciwdomeny. Innymi słowy, Y jest pokolorowane w dwuetapowym procesie: Po pierwsze, dla każdego x w X , punkt f ( x ) jest pokolorowany na żółto; Po drugie, wszystkie pozostałe punkty w Y , które nie są żółte, mają kolor niebieski. Funkcja f byłaby surjektywna tylko wtedy, gdyby nie było niebieskich punktów.

Dla dowolnego zbioru X The funkcja tożsamości id _X na X jest suriekcją.
Funkcja $f : Z \to {0, 1}$ zdefiniowana przez f ( n ) = n mod 2 (to znaczy parzyste liczby całkowite są odwzorowywane na 0, a nieparzyste na 1) jest surjektywne.
Funkcja $f : R \to R$ określona przez f ( x ) = 2 x + 1 jest surjektywna (a nawet bijektywna ), ponieważ dla każdej liczby rzeczywistej y mamy x takie, że f ( x ) = y : takie odpowiednie x jest ( y − 1)/2.
Funkcja $f : R \to R$ określona przez f ( x ) = x ³ − 3 x jest surjektywna, ponieważ wstępny obraz dowolnej liczby rzeczywistej y jest zbiorem rozwiązań równania wielomianu sześciennego x ³ − 3 x − y = 0 , a każdy wielomian sześcienny o współczynnikach rzeczywistych ma co najmniej jeden pierwiastek rzeczywisty. Jednak ta funkcja nie jest iniektywna (a zatem nie jest bijektywna ), ponieważ na przykład przedobraz y = 2 to { x = -1, x = 2}. (W rzeczywistości wstępny obraz tej funkcji dla każdego y , -2 ≤ y ≤ 2 ma więcej niż jeden element.)
Funkcja $g : R \to R$ określona przez g ( x ) = x ² nie jest surjektywna, ponieważ nie istnieje liczba rzeczywista x taka, że x ² = −1 . Jednak funkcja $g : R \to R \geq0$ określona przez $g (x) = x 2$ (z ograniczoną przeciwdziedziną) jest surjektywna, ponieważ dla każdego y w nieujemnej rzeczywistej przeciwdziedzinie Y istnieje co najmniej jeden x w rzeczywistej domenie X takie, że x ² = y .
Logarytm naturalny funkcja $ln (0 + \infty) \to R$ jest suriekcją nawet bijective (mapowanie ze zbioru liczb rzeczywistych dodatnich do zbioru liczb rzeczywistych). Jej odwrotność, funkcja wykładnicza , jeśli jest zdefiniowana ze zbiorem liczb rzeczywistych jako dziedziną, nie jest surjektywna (ponieważ jej zakres jest zbiorem dodatnich liczb rzeczywistych).
Wykładniczy matryca nie jest suriekcją widziane jako mapa z przestrzeni wszystkich n x n macierzy do siebie. Definiuje się go jednak zwykle jako odwzorowanie z przestrzeni wszystkich macierzy n × n do ogólnej grupy liniowej stopnia n (czyli grupy wszystkich n × n macierzy odwracalnych ). Zgodnie z tą definicją, macierz wykładnicza jest surjektywna dla macierzy złożonych, choć nadal nie jest surjektywna dla macierzy rzeczywistych.
Występ z iloczyn kartezjański $x$ $B$ do jednego z jego parametrów jest suriekcją, chyba że drugi czynnik jest pusta.
W grze wideo 3D wektory są rzutowane na płaski ekran 2D za pomocą funkcji surjektywnej.

Interpretacja funkcji surjektywnych na płaszczyźnie kartezjańskiej, określonych przez odwzorowanie f : X → Y , gdzie y = f ( x ), X = dziedzina funkcji, Y = zakres funkcji. Każdy element w zakresie jest mapowany z elementu w domenie zgodnie z regułą f . Może istnieć wiele elementów domeny, które są mapowane na ten sam element zakresu. Oznacza to, że każdy y w Y jest mapowany z elementu x w X , więcej niż jeden x może mapować do tego samego y . Po lewej: Pokazana jest tylko jedna domena, co sprawia, że f jest surjektywne. Po prawej: pokazane są dwie możliwe domeny X ₁ i X ₂ .

Funkcje niesuriektywne na płaszczyźnie kartezjańskiej. Chociaż niektóre części funkcji są surjektywne, gdzie elementy y w Y mają wartość x w X taką, że y = f ( x ), niektóre części nie. Po lewej: jest y ₀ w Y , ale nie ma x ₀ w X takie, że y ₀ = f ( x ₀ ). Po prawej: są y ₁ , y ₂ i y ₃ w Y , ale nie ma x ₁ , x ₂ i x ₃ w X takich, że y ₁ = f ( x ₁ ), y ₂ = f ( x ₂ ), i r ₃ = f ( x ₃ ).

Nieruchomości

Funkcja jest bijektywna wtedy i tylko wtedy, gdy jest zarówno surjektywna, jak i iniekcyjna .

Jeśli (jak to często się robi) funkcja jest identyfikowana z jej wykresem , to suriektywność nie jest właściwością samej funkcji, ale raczej właściwością odwzorowania . To jest funkcja wraz z jej domeną. W przeciwieństwie do injektywności, suriektywności nie można odczytać z samego wykresu funkcji.

Surjekcje jako prawidłowe funkcje odwracalne

Funkcja g : Y → X jest odwrotnością funkcji f : X → Y jeśli f ( g ( y )) = y dla każdego y w Y ( g można cofnąć przez f ). Innymi słowy, g jest tuż odwrotną f , gdy kompozycja F O g o g i f w tym celu jest funkcja tożsamości w domenie Y z g . Funkcja g nie musi być kompletna odwrotny z f , gdyż skład się w innej kolejności, g O F , może być funkcja tożsamości w domenie X o F . Innymi słowy, f może cofnąć lub " odwrócić " g , ale niekoniecznie musi być przez nie odwrócone.

Każda funkcja z prawą odwrotnością jest z konieczności odrzuceniem. Twierdzenie, że każda funkcja surjektywna ma prawo odwrotne, jest równoważne aksjomatowi wyboru .

Jeśli f : X → Y jest suriekcją i B jest podzbiorem z Y , a f ( f ^-1 ( B )) = B . W ten sposób B można odzyskać z jego obrazu wstępnego f- ¹ ( B ) .

Na przykład na pierwszej ilustracji powyżej jest jakaś funkcja g taka, że g ( C ) = 4. Istnieje również pewna funkcja f taka , że f (4) = C . Nie ma znaczenia, że g ( C ) również może być równe 3; liczy się tylko to, że f "odwraca" g .

Kompozycja surjektywna: pierwsza funkcja nie musi być surjektywna.
Kolejna funkcja surjektywna. (Ten okazuje się być bijekcją )
Non funkcja -surjective. (To jest zastrzyk )

Surjekcje jako epimorfizmy

Funkcja f : X → Y jest surjektywna wtedy i tylko wtedy , gdy jest prawostronnie anulowana : biorąc pod uwagę dowolne funkcje g , h : Y → Z , zawsze gdy g o f = h o f , wtedy g = h . Ta właściwość jest formułowane w kategoriach funkcji i ich kompozycji i mogą być uogólnione na bardziej ogólnym pojęciu morfizmów o kategorii i ich kompozycji. Morfizmy prawostronne są nazywane epimorfizmami . W szczególności funkcje surjektywne to właśnie epimorfizmy w kategorii zbiorów . Przedrostek epi pochodzi od greckiego przyimka ἐπί oznaczającego ponad , powyżej , na .

Każdy morfizm z prawą odwrotnością jest epimorfizmem, ale odwrotność nie jest generalnie prawdziwa. Prawo odwrotny g z morfizmem f nazywa się odcinek o f . Morfizm z odwrotnością prawostronną nazywany jest epimorfizmem rozszczepionym .

Surjekcje jako relacje binarne

Każda funkcja z domeną X i kodziedziną Y może być postrzegana jako binarna relacja lewo-całkowita i prawa-unikatowa między X i Y , identyfikując ją z jej wykresem funkcji . Funkcja surjektywna z domeną X i kodziedziną Y jest zatem relacją binarną między X i Y, która jest jednoznaczna dla prawej strony oraz zarówno dla lewo-całkowitej, jak i prawo-całkowitej .

Liczność domeny przyrzeczenia

Liczność domeny o suriekcją funkcji jest większa niż lub równa liczności jego codomain: jeśli f : X → Y jest suriekcją funkcji, a X ma co najmniej wielu elementów, jak Y , w sensie liczby stron świata . (Dowód odwołań do pewnik wyboru , aby pokazać, że funkcja g : Y → X spełniających f ( g ( Y )) = y dla wszystkich Y w Y , istnieje g łatwo zauważyć się za pomocą wstrzyknięć, w ten sposób formalny definicji z | Y | ≤ | X | jest spełniony.)

W szczególności, jeśli zarówno X, jak i Y są skończone z tą samą liczbą elementów, wtedy f : X → Y jest surjektywne wtedy i tylko wtedy, gdy f jest injekcyjne .

Mając dwa zbiory X i Y , notacja X ≤ ^* Y jest używana do powiedzenia, że albo X jest puste, albo że istnieje sujekcje z Y na X . Używając aksjomatu wyboru można pokazać, że X ≤ ^* Y i Y ≤ ^* X razem implikują, że | Y | = | X |, wariant twierdzenia Schrödera-Bernsteina .

Skład i rozkład

Skład funkcji suriekcją zawsze suriekcją: jeśli f i g są zarówno suriekcją i codomain z g odpowiada domenie F , a f O g znaczy suriekcją. I odwrotnie, jeśli f o g jest surjektywna, to f jest surjekcyjna (ale g , funkcja zastosowana jako pierwsza, nie musi być). Właściwości te uogólniają się od przyjęć w kategorii zbiorów do dowolnych epimorfizmów w dowolnej kategorii .

Każda funkcja może być rozłożona na surjection i iniekcji : dla każdej funkcji h : X → Z nie istnieć surjection f : X → Y i wtrysku g : Y → Z , tak że H = g O F . Aby to zobaczyć, zdefiniuj Y jako zbiór wstępnych obrazów h ^-1 ( z ), gdzie z jest w h ( X ) . Te obrazy wstępne są rozłączne i podzielone na partycje X . Wtedy f przenosi każdy x do elementu Y, który go zawiera, a g przenosi każdy element Y do punktu w Z, do którego h wysyła swoje punkty. Wtedy f jest surjektywne, ponieważ jest odwzorowaniem projekcyjnym, a g jest z definicji iniektywne.

Indukowana surjekcja i indukowana bijekcja

Każda funkcja indukuje surjekcję, ograniczając swoją kodomenę do swojego zakresu. Każda funkcja surjektywna indukuje bijekcję zdefiniowaną na ilorazie swojej dziedziny przez zbicie wszystkich argumentów mapujących dany nieruchomy obraz. Dokładniej, każda surjekcja f : A → B może być rozłożona jako projekcja, po której następuje bijekcja w następujący sposób. Niech / ~ BE klas równoważności z A na poniższej równoważnikowego stosunku : x ~ y wtedy i tylko wtedy, f ( x ) = f ( T ). Równoważnie A /~ jest zbiorem wszystkich obrazów wstępnych pod f . Niech P (~) : A → A /~ będzie odwzorowaniem, które wysyła każdy x w A do jego klasy równoważności [ x ] _~ , i niech f _P : A /~ → B będzie dobrze zdefiniowaną funkcją podaną przez f _P ([ x ] _~ ) = f ( x ). Wtedy f = f _P o P (~).

Zobacz też

Bibliografia

Dalsza lektura

Bourbaki, N. (2004) [1968]. Teoria zbiorów . Elementy matematyki . 1 . Skoczek. doi : 10.1007/978-3-642-59309-3 . Numer ISBN 978-3-540-22525-6. LCCN 2004110815 .

Languages

In other projects