Sześcian Tetrakis - Tetrakis hexahedron

Sześcian Tetrakis
Tetrakishexahedron.jpg
(Kliknij tutaj, aby wyświetlić model obrotowy)
Rodzaj Katalońskie ciało stałe
Diagram Coxetera Węzeł CDel f1.pngCDel 3.pngWęzeł CDel f1.pngCDel 4.pngCDel node.png
Węzeł CDel f1.pngCDel 3.pngWęzeł CDel f1.pngCDel 3.pngWęzeł CDel f1.png
Notacja Conwaya kC
Typ twarzy V4.6.6
DU08 facets.png

Trójkąt równoramienny
Twarze 24
Krawędzie 36
Wierzchołki 14
Wierzchołki według typu 6 {4} +8 {6}
Grupa symetrii O h , B 3 , [4,3], (* 432)
Grupa rotacyjna O, [4,3] + , (432)
Kąt dwuścienny 143 ° 07′48 ″
arccos (- 4 / 5 )
Nieruchomości wypukłe, przechodnie przez twarz
Obcięty octahedron.png
Ścięty ośmiościan
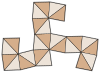( podwójny wielościan ) 		Tetrakis hexahedron Net
Netto
Podwójnego związku z ośmiościan ścięty i tetrakis sześciościenny. Drzeworyt po lewej stronie pochodzi z Perspectiva Corporum Regularium (1568) autorstwa Wenzela Jamnitzera .
Model matrycy i kryształu
Rysunek i model kryształu wariantu o symetrii czworościennej zwanego czworościanem heksakis

W geometrii , A tetrakis sześciokąt (znany również jako tetrahexahedron , sześcian piramidalny , tetrakis kostki i kiscube ) jest kataloński stałej . Jego dwoistość to oktaedr ścięty , bryła archimedesa .

To również może być nazywany pręt sześciokątny disdyakis lub heksakis czworościanu jak podwójny o omnitruncated czworościanu .

współrzędne kartezjańskie

Współrzędne kartezjańskie dla 14 wierzchołków sześcianu tetrakisa wyśrodkowanych na początku to punkty (± 3/2, 0, 0), (0, ± 3/2, 0), (0, 0, ± 3/2) i (± 1, ± 1, ± 1).

Długość krótszych krawędzi tego sześcianu tetrakisa wynosi 3/2, a dłuższych krawędzi równa się 2. Twarze są ostrymi trójkątami równoramiennymi. Większy kąt jest równy, a dwa mniejsze równe .

Rzuty ortogonalne

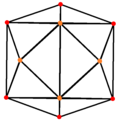
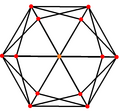
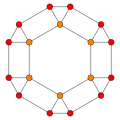
Sześciokąt tetrakis , dwa z ośmiościan ścięty ma 3 pozycji symetrii dwóch umieszczonych na wierzchołkach i jeden połowie krawędzi.

Rzuty ortogonalne
rzutowe
symetria 		[2] [4] [6]

Sześcian Tetrakis 		Podwójna kostka t12 e66.png Podwójna kostka t12 B2.png Podwójna kostka t12.png
Ścięty
ośmiościan 		Cube t12 e66.png 3-cube t12 B2.svg 3-kostka t12.svg

Używa

Naturalnie występujące ( krystaliczne ) formacje tetraheksaedrów obserwuje się w układach miedzianych i fluorytowych .

Wielościenne kości w kształcie sześcianu tetrakisa są czasami używane przez graczy .

24 komórek oglądany w wierzchołek pierwszego perspektywicznym rzucie ma topologii powierzchni sześcianu tetrakis i geometrycznych proporcjach rombowego dwunastościanu , z rombowego powierzchnie podzielone na dwa trójkąty.

Sześcian tetrakis pojawia się jako jeden z najprostszych przykładów w teorii budownictwa . Rozważmy symetryczną przestrzeń riemannowską związaną z grupą SL 4 ( R ) . Jego granica cycki ma strukturę kulistego budynku, którego mieszkania są dwuwymiarowymi kulami. Podział tej sfery na kuliste prostoty (komory) można uzyskać, biorąc rzut promieniowy sześcianu tetrakisa.

Symetria

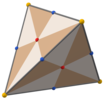
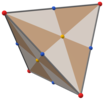
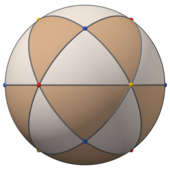
Przy Td , [3,3] (* 332) symetrii czworościennej , trójkątne ściany reprezentują 24 podstawowe domeny symetrii czworościennej. Ten wielościan można zbudować z 6 wielkich okręgów na kuli. Można go również zobaczyć jako sześcian z kwadratowymi ścianami wytyczonymi przez trójkąty wierzchołkami i środkami ścian oraz czworościanem z ścianami podzielonymi wierzchołkami, środkowymi krawędziami i punktem centralnym.

Wielościan wielki romb 4-4 max.png Disdyakis 6 max.png Disdyakis 6 w deltoidal 12.png Disdyakis 6 in rhombic 6 max.png Disdyakis 6 w Platonic 4a max.png Disdyakis 6 w Platonic 4b max.png
obcinane
tetratetrahedron
Sześcian Disdyakis
Dwunastościan naramienny 		Rombowy
sześcian 		Czworościan

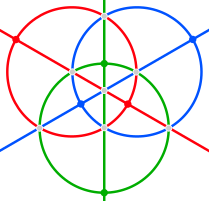
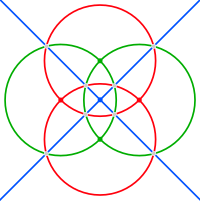
Krawędzie kulistego sześcianu tetrakisa należą do sześciu wielkich okręgów, które odpowiadają lustrzanym płaszczyznom w czworościennej symetrii . Można je pogrupować w trzy pary ortogonalnych okręgów (które zwykle przecinają się na jednej osi współrzędnych). Na poniższych zdjęciach te kwadratowe hosoedry są w kolorze czerwonym, zielonym i niebieskim.

Wymiary

Jeśli oznaczymy długość krawędzi sześcianu podstawy przez a , wysokość każdego szczytu piramidy nad sześcianem wynosi za / 4 . Nachylenie każdej trójkątnej ściany piramidy względem ściany sześcianu jest arctan ( 1 / 2 ), około 26,565 ° (sekwencja A073000 w OEIS ). Jedna krawędź trójkątów równoramiennych ma długość a , pozostałe dwa mają długość 3 a / 4 , co następuje przez zastosowanie twierdzenia Pitagorasa do wysokości i długości podstawy. Daje to wysokość √ 5 a / 4 w trójkącie ( OEIS :  A204188 ). Jego obszar to √ 5 a / 8 , a kąty wewnętrzne to arccos ( 2 / 3 ) (około 48,1897 °) i uzupełniające 180 ° - 2 arccos ( 2 / 3 ) (około 83,6206 °).

Objętość piramidy jest a 3 / 12 ; więc całkowita objętość sześciu piramid i sześcianu w sześcianie wynosi 3 a 3 / 2 .

Kleetope

Można go postrzegać jako sześcian z kwadratowymi piramidami pokrywającymi każdą kwadratową ścianę; to znaczy jest to Kleetope sześcianu.

Sześcienna piramida

Jest bardzo podobny do siatki 3D dla piramidy sześciennej 4D , ponieważ siatka dla kwadratu jest kwadratem z trójkątami przymocowanymi do każdej krawędzi, siatka dla piramidy sześciennej to sześcian z kwadratowymi piramidami przymocowanymi do każdej ściany.

Powiązane wielościany i dachówki

Jest to wielościan w kolejności określonej przez konfigurację ścian V4.6.2 n . Ta grupa jest wyjątkowa, ponieważ ma wszystkie parzyste liczby krawędzi na wierzchołek i tworzy dwusieczne płaszczyzny przez wielościany i nieskończone linie w płaszczyźnie i przechodząc do płaszczyzny hiperbolicznej dla dowolnego n  ≥ 7.

Przy parzystej liczbie ścian w każdym wierzchołku, te wielościany i nachylenia można wyświetlić naprzemiennie w dwóch kolorach, tak aby wszystkie sąsiednie ściany miały różne kolory.

Każda ściana w tych domenach odpowiada również podstawowej domenie grupy symetrii z rzędem 2, 3, n luster w każdym wierzchołku ściany trójkąta.

Zobacz też

Bibliografia

  • Williams, Robert (1979). Geometryczna podstawa struktury naturalnej: książka źródłowa projektowania . ISBN firmy Dover Publications, Inc.   0-486-23729-X . (Rozdział 3-9)
  • Wenninger, Magnus (1983), podwójne modele , Cambridge University Press , doi : 10.1017 / CBO9780511569371 , ISBN   978-0-521-54325-5 , MR   0730208 (Trzynaście półregularnych wypukłych wielościanów i ich podwójnych, Strona 14, Tetrakishexahedron)
  • The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN   978-1-56881-220-5 [1] (Rozdział 21, Nazewnictwo wielościanów Archimedesa i Katalonii oraz tilings, strona 284, Tetrakis hexahedron )

Linki zewnętrzne