Drzewo prymitywnych trójek pitagorejskich - Tree of primitive Pythagorean triples

W matematyce , o drzewo prymitywnych Pitagorasa trójek jest drzewo danych , w której każdy węzeł gałęzie do trzech kolejnych węzłów z nieskończonego zbioru wszystkich węzłów dając wszystko (i jedyny) prymitywne Pitagorasa trójek bez powielania.

Pitagorasa potrójne jest zestaw trzech dodatnich liczb całkowitych a, b, i C mające tę właściwość, że mogą one być, odpowiednio, dwa ramiona i przeciwprostokątną z trójkąta prostokątnego , w ten sposób, spełniające równanie ; potrójne mówi się prymitywny wtedy i tylko wtedy, gdy największy wspólny dzielnik z A, B i C, wynosi jeden. Pierwotne pitagorejskie potrójne a, b i c są również parami względnie pierwsze . Zbiór wszystkich prymitywnych trójek pitagorejskich ma w naturalny sposób strukturę zakorzenionego drzewa , a konkretnie drzewa trójskładnikowego . Po raz pierwszy odkrył to B. Berggren w 1934 roku. ${\ Displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$

FJM Barning pokazał, że gdy którakolwiek z trzech macierzy

${\ displaystyle {\ begin {tablica} {lcr} A = {\ początek {bmatrix} 1 i -2 i 2 \\ 2 i -1 i 2 \\ 2 i -2 i 3 \ koniec {bmatrix}} i B = {\ początek {bmatrix} 1 i 2 i 2 \\ 2 & 1 & 2 \\ 2 & 2 & 3 \ end {bmatrix}} & C = {\ begin {bmatrix} -1 & 2 & 2 \\ - 2 & 1 & 2 \\ - 2 & 2 & 3 \ end {bmatrix}} \ end {array}}}$

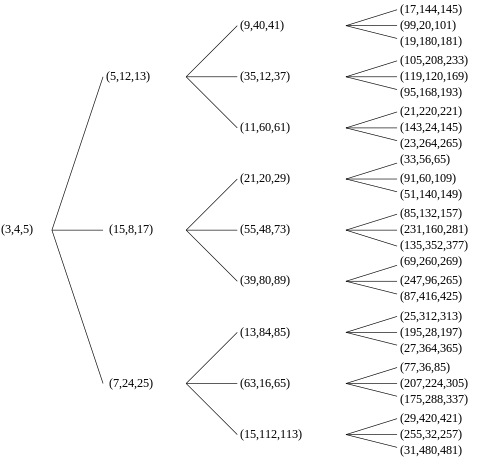
jest mnożony po prawej stronie przez wektor kolumnowy, którego składowe tworzą trójkę pitagorejską, a wynikiem jest inny wektor kolumnowy, którego składowe są inną trójką pitagorejską. Jeśli początkowa trójka jest prymitywna, tak samo jest z wynikiem. Zatem każda prymitywna trójka pitagorejska ma troje „dzieci”. Wszystkie pierwotne trójki pitagorejskie wywodzą się w ten sposób z trójki (3, 4, 5) i żadna pierwotna trójka nie pojawia się więcej niż raz. Wynik można przedstawić graficznie jako nieskończone drzewo trójskładnikowe z (3, 4, 5) w węźle głównym (patrz klasyczne drzewo po prawej). Drzewo to pojawiło się również w pracach A. Halla w 1970 r. I AR Kanga w 1990 r. W 2008 r. VE Firstov wykazał ogólnie, że istnieją tylko trzy takie drzewa trychotomiczne i wyraźnie dają drzewo podobne do drzewa Berggrena, ale zaczynające się od węzła początkowego (4, 3, 5 ).

Dowody

Obecność wyłącznie prymitywnych trójek pitagorejskich

Można wykazać indukcyjnie, że drzewo zawiera prymitywne trójki pitagorejskie i nic więcej, pokazując, że począwszy od prymitywnej trójki pitagorejskiej, takiej jak jest obecna w początkowym węźle z (3, 4, 5), każda wygenerowana trójka jest zarówno pitagorejska, jak i prymitywna .

Zachowanie własności pitagorejskiej

Jeśli którakolwiek z powyższych macierzy, powiedzmy A , zostanie zastosowana do potrójnej ( a , b , c ) ^T mającej właściwość Pitagorasa a ² + b ² = c ^2, aby otrzymać nową trójkę ( d , e , f ) ^T = A ( a , b , c ) ^T , ta nowa trójka jest również pitagorejską. Można to zobaczyć, wypisując każdy z d , e i f jako sumę trzech wyrazów w a , b i c , podnosząc każdy z nich do kwadratu i podstawiając c ² = a ² + b ^2, aby otrzymać f ² = d ² + e ² . Odnosi się to do B i C , jak również dla A .

Zachowanie prymitywności

Wszystkie macierze A , B i C są unimodularne - to znaczy mają tylko wpisy w postaci liczb całkowitych, a ich wyznaczniki wynoszą ± 1. Zatem ich odwrotności są również jednomodułowe i mają w szczególności tylko wpisy w postaci liczb całkowitych. Więc jeśli którykolwiek z nich, na przykład A , zostanie zastosowany do prymitywnej potrójnej pitagorejskiej ( a , b , c ) ^T, aby otrzymać kolejną trójkę ( d , e , f ) ^T , mamy ( d , e , f ) ^T = ( , b , c ) ^{, T} , a więc ( , b , c ) ^{, T} = ^-1 ( d , e , f ) ^T . Gdyby jakikolwiek czynnik pierwszy był wspólny dla dowolnych dwóch (a zatem wszystkich trzech) d , e i f, to według tego ostatniego równania ta liczba pierwsza również podzieliłaby każde z a , b i c . Więc jeśli a , b i c są w rzeczywistości parami względnie pierwsze, to d , e i f również muszą być parami względnie pierwsze. Odnosi się to do B i C , jak również dla A .

Obecność każdej prymitywnej pitagorejskiej trójki dokładnie raz

Aby pokazać, że drzewo zawiera każdą prymitywną trójkę pitagorejską, ale nie więcej niż raz, wystarczy wykazać, że dla każdej takiej trójki istnieje dokładnie jedna ścieżka z powrotem przez drzewo do węzła początkowego (3, 4, 5). Można to zobaczyć, stosując kolejno każdą z unimodularnych macierzy odwrotnych A ⁻¹ , B ⁻¹ i C ⁻¹ do dowolnej prymitywnej potrójnej pitagorejskiej ( d , e , f ), zauważając, że dzięki powyższej prymitywności rozumowania i pitagorejskiej właściwości są zachowane i zauważając, że dla każdego potrójnego większego niż (3, 4, 5) dokładnie jedna z macierzy odwrotnego przejścia daje nową trójkę ze wszystkimi dodatnimi wpisami (i mniejszą przeciwprostokątną). Przez indukcję ta nowa ważna trójka sama prowadzi do dokładnie jednej mniejszej, prawidłowej trójki i tak dalej. Dzięki skończoności liczby mniejszych i mniejszych potencjalnych przeciwprostokątnych ostatecznie osiąga się (3, 4, 5). Dowodzi to, że ( d , e , f ) faktycznie występuje w drzewie, ponieważ można do niego dotrzeć z (3, 4, 5) odwracając kroki; i występuje wyjątkowo, ponieważ istniała tylko jedna ścieżka od ( d , e , f ) do (3, 4, 5).

Nieruchomości

Transformacja wykorzystująca macierz A , jeśli jest wykonywana wielokrotnie od ( a ,  b ,  c ) = (3, 4, 5), zachowuje cechę b  + 1 =  c ; macierz B zachowuje a  -  b  = ± 1 zaczynając od (3, 4, 5); a macierz C zachowuje cechę a  + 2 =  c począwszy od (3, 4, 5).

Interpretacja geometryczna tego drzewa obejmuje excircles obecne w każdym węźle. Troje dzieci dowolnego trójkąta rodzicielskiego „dziedziczy” swoje inradii od rodzica: promienie wykrętu rodzica stają się inradii dla następnego pokolenia. Na przykład rodzic (3, 4, 5) ma zaokrąglone promienie równe 2, 3 i 6. Są to dokładnie inradii trojga dzieci (5, 12, 13), (15, 8, 17) i (21, 20, 29) .

Jeśli jedno z A lub C zostanie zastosowane wielokrotnie z dowolnej potrójnej pitagorejskiej użytej jako warunek początkowy, wówczas dynamikę dowolnego z a , b i c można wyrazić jako dynamikę x w

${\ Displaystyle x_ {n + 3} -3x_ {n + 2} + 3x_ {n + 1} -x_ {n} = 0 \,}$

która jest wzorowana na wspólnym równaniu charakterystycznym macierzy

${\ Displaystyle \ lambda ^ {3} -3 \ lambda ^ {2} +3 \ lambda -1 = 0. \,}$

Jeśli B jest stosowane wielokrotnie, to dynamika dowolnej z a , b i c może być wyrażona jako dynamika x w

${\ Displaystyle x_ {n + 3} -5x_ {n + 2} -5x_ {n + 1} + x_ {n} = 0, \,}$

która jest umieszczona na charakterystycznego równania B .

Ponadto nieskończoność innych równań różnicowych jednowymiarowych trzeciego rzędu można znaleźć, mnożąc dowolną z trzech macierzy razem dowolną liczbę razy w dowolnej kolejności. Na przykład macierz D  =  CB przesuwa jeden krok poza drzewo o dwa węzły (w poprzek, a następnie w dół) w jednym kroku; charakterystyczne równanie D stanowi wzorzec dla dynamiki trzeciego rzędu dowolnego a ,  b, i c w niewyczerpujący drzewa utworzonej przez  D .

Alternatywne metody generowania drzewa

Inne podejście do dynamiki tego drzewa opiera się na standardowej formule generowania wszystkich prymitywnych trójek pitagorejskich:

${\ Displaystyle a = m ^ {2} -n ^ {2}, \,}$

${\ Displaystyle b = 2 mln, \,}$

${\ Displaystyle c = m ^ {2} + n ^ {2}, \,}$

gdzie m  >  n  > 0 i m i n względnie pierwsze io przeciwnej parzystości. Pary ( m ,  n ) można iterować przez wstępne pomnożenie ich (wyrażone jako wektor kolumnowy) przez dowolną z

${\ displaystyle {\ begin {array} {lcr} {\ begin {bmatrix} 2 & -1 \\ 1 & 0 \ end {bmatrix}}, & {\ begin {bmatrix} 2 i 1 \\ 1 & 0 \ end {bmatrix}}, & {\ begin {bmatrix} 1 & 2 \\ 0 & 1 \ end {bmatrix}}, \ end {tablica}}}$

z których każdy zachowuje nierówności, bezpretensjonalność i przeciwny parytet. Wynikowe drzewo trójskładnikowe, zaczynając od (2,1), zawiera każdą taką ( m ,  n ) parę dokładnie raz, a po przeliczeniu na ( a ,  b ,  c ) trójki staje się identyczne z drzewem opisanym powyżej.

Innym sposobem wykorzystania dwóch podstawowych parametrów do wygenerowania drzewa trójek jest alternatywna formuła dla wszystkich pierwotnych trójek:

${\ displaystyle a = uv, \,}$

${\ Displaystyle b = {\ Frac {u ^ {2} -v ^ {2}} {2}},}$

${\ Displaystyle c = {\ Frac {u ^ {2} + v ^ {2}} {2}},}$

przy u  >  v  > 0 i U i V względnie pierwsze i obie nieparzyste . Pary ( u ,  v ) mogą być iterowane przez wstępne pomnożenie ich (wyrażone jako wektor kolumnowy) przez dowolną z powyższych macierzy 2 × 2, z których wszystkie trzy zachowują nierówności, względność i nieparzystą parzystość obu elementów. Kiedy ten proces rozpoczyna się w (3, 1), otrzymane drzewo trójskładnikowe zawiera każdą taką parę ( u ,  v ) dokładnie raz, a po konwersji na ( a ,  b ,  c ) potrójne, staje się identyczne z drzewem opisanym powyżej.

Inne drzewo

Alternatywnie można również użyć 3 różnych macierzy znalezionych przez Price. Te macierze A ', B', C ' i odpowiadające im transformacje liniowe są pokazane poniżej.

${\ Displaystyle {\ overset {{A} '} {\ mathop {\ lewo [{\ początek {macierz} 2 i 1 i -1 \\ - 2 i 2 i 2 \\ - 2 i 1 i 3 \ koniec {macierz}} \ prawej]}}} \ lewo [{\ begin {matrix} a \\ b \\ c \ end {matrix}} \ right] = \ left [{\ begin {matrix} a_ {1} \\ b_ {1} \\ c_ {1} \ end {matrix}} \ right], \ quad {\ text {}} {\ overset {{B} '} {\ mathop {\ left [{\ begin {matrix} 2 i 1 i 1 \\ 2 i -2 i 2 \\ 2 i -1 i 3 \ end {matrix}} \ right]}}} \ left [{\ begin {matrix} a \\ b \\ c \\\ end {matrix}} \ right] = \ left [{\ begin {matrix} a_ {2} \\ b_ {2} \\ c_ {2} \ end {matrix}} \ right], \ quad {\ text {}} {\ overset {{C} '} {\ mathop {\ left [{ \ begin {matrix} 2 & -1 & 1 \\ 2 & 2 & 2 \\ 2 & 1 & 3 \\\ end {matrix}} \ right]}}} \ left [{\ begin {matrix} a \\ b \\ c \\\ end {matrix} }} \ right] = \ left [{\ begin {matrix} a_ {3} \\ b_ {3} \\ c_ {3} \ end {matrix}} \ right]}$

Trzy transformacje liniowe Price'a to

${\ Displaystyle {\ rozpocząć {wyrównane} i {\ rozpocząć {macierz} + 2a + bc = a_ {1} \ quad i -2a + 2b + 2c = b_ {1} \ quad i -2a + b + 3c = c_ {1} & \ quad \ to \ left [{\ text {}} a_ {1}, {\ text {}} b_ {1}, {\ text {}} c_ {1} \ right] \ end {matrix }} \\ & {\ begin {matrix} + 2a + b + c = a_ {2} \ quad & + 2a-2b + 2c = b_ {2} \ quad & + 2a-b + 3c = c_ {2} & \ quad \ to \ left [{\ text {}} a_ {2}, {\ text {}} b_ {2}, {\ text {}} c_ {2} \ right] \ end {matrix}} \ \ & {\ begin {matrix} + 2a-b + c = a_ {3} \ quad & + 2a + 2b + 2c = b_ {3} \ quad & + 2a + b + 3c = c_ {3} & \ quad \ to \ left [{\ text {}} a_ {3}, {\ text {}} b_ {3}, {\ text {}} c_ {3} \ right] \ end {matrix}} \\ & \ koniec {aligned}}}$

Troje elementów potomnych tworzone przez każdy z dwóch zestawów macierzy nie są takie same, ale każdy zestaw osobno tworzy wszystkie pierwotne trójki.

Na przykład używając [5, 12, 13] jako rodzica, otrzymujemy dwa zestawy trojga dzieci:

${\ Displaystyle {\ rozpocząć {tablicę} {CCC} & \ lewo [5,12,13 \ prawo] & \\ A & B & C \\\ lewo [45,28,53 \ prawo] i \ lewo [55,48,73 \ right] & \ left [7,24,25 \ right] \ end {array}} \ quad \ quad \ quad \ quad \ quad \ quad {\ begin {array} {ccc} {} & \ left [5, 12,13 \ right] & {} \\ A '& B' & C '\\\ left [9,40,41 \ right] & \ left [35,12,37 \ right] & \ left [11,60, 61 \ right] \ end {tablica}}}$

Uwagi i odniesienia

Zewnętrzne linki

• Drzewo (-a) trójargumentowe leżące u podstaw prymitywnych pitagorejskich Potrójnych w przecięciu węzła
• Frank R. Bernhart i H. Lee Price, „Pythagoras 'garden, revisited”, Australian Senior Mathematics Journal 01/2012; 26 (1): 29-40. [1]
• Weisstein, Eric W. „Potrójny pitagorejski” . MathWorld .