Krzywa Béziera -Bézier curve

Sześcienna krzywa Béziera z czterema punktami kontrolnymi

Funkcje bazowe w zakresie t w [0,1] dla sześciennych krzywych Béziera: niebieski: y = (1 − t ) ³ , zielony: y = 3(1 − t ) ² t , czerwony: y = 3(1 − t ) t ² , i cyjan: y = t ³ .

Krzywa Béziera ( / b ɛ z . I . eɪ / BEH -zee-ay ) to parametryczna krzywa używana w grafice komputerowej i dziedzinach pokrewnych. Zbiór dyskretnych „punktów kontrolnych” definiuje gładką, ciągłą krzywą za pomocą wzoru. Zwykle krzywa ma na celu przybliżenie rzeczywistego kształtu, który w przeciwnym razie nie ma matematycznej reprezentacji lub którego reprezentacja jest nieznana lub zbyt skomplikowana. Krzywa Béziera została nazwana na cześć francuskiego inżyniera Pierre'a Béziera , który wykorzystał ją w latach 60. do zaprojektowania krzywych dla karoserii Renaultsamochody. Inne zastosowania obejmują projektowanie czcionek komputerowych i animacji. Krzywe Béziera można łączyć, tworząc splajn Béziera , lub uogólniać na większe wymiary, tworząc powierzchnie Béziera . Trójkąt Béziera jest szczególnym przypadkiem tego ostatniego.

W grafice wektorowej krzywe Béziera są używane do modelowania gładkich krzywych, które można skalować w nieskończoność. „Ścieżki”, jak są one powszechnie określane w programach do obróbki obrazu, to kombinacje połączonych krzywych Béziera. Ścieżki nie są ograniczone ograniczeniami zrasteryzowanych obrazów i można je intuicyjnie modyfikować.

Krzywe Béziera są również używane w dziedzinie czasu, szczególnie w animacji , projektowaniu interfejsów użytkownika i wygładzaniu trajektorii kursora w interfejsach kontrolowanych wzrokiem. Na przykład krzywej Béziera można użyć do określenia prędkości obiektu, takiego jak ikona, przemieszczającego się z punktu A do punktu B w czasie, zamiast po prostu poruszać się ze stałą liczbą pikseli na krok. Kiedy animatorzy lub projektanci interfejsów mówią o „fizyce” lub „odczuciu” operacji, mogą odnosić się do konkretnej krzywej Béziera używanej do kontrolowania prędkości danego ruchu w czasie.

Dotyczy to również robotyki, w której ruch np. ramienia spawalniczego powinien być płynny, aby uniknąć niepotrzebnego zużycia.

Wynalazek

Matematyczna podstawa krzywych Béziera - wielomiany Bernsteina - została ustalona w 1912 r., Ale wielomiany zostały zastosowane w grafice dopiero około 50 lat później, kiedy matematyk Paul de Casteljau w 1959 r. Opracował algorytm de Casteljau , numerycznie stabilną metodę oceny krzywych, i jako pierwszy zastosował je do projektowania wspomaganego komputerowo we francuskim producencie samochodów Citroën . Jednak metoda de Casteljau została opatentowana we Francji, ale opublikowana dopiero w latach 80. XX wieku, podczas gdy wielomiany Béziera zostały szeroko nagłośnione w latach 60. XX wieku przez francuskiego inżyniera Pierre'a Béziera , który odkrył je niezależnie i wykorzystał do projektowania karoserii samochodów w Renault .

Konkretne przypadki

Krzywa Béziera jest zdefiniowana przez zbiór punktów kontrolnych od P0 do _Pn , gdzie _n nazywa się rzędem krzywej ( n = 1 dla liniowej, 2 dla kwadratowej, 3 dla sześciennej itd.). Pierwszy i ostatni punkt kontrolny są zawsze punktami końcowymi krzywej; jednakże pośrednie punkty kontrolne (jeśli występują) generalnie nie leżą na krzywej. Sumy w kolejnych sekcjach należy rozumieć jako kombinacje afiniczne – czyli suma współczynników wynosi 1.

Liniowe krzywe Béziera

Biorąc pod uwagę różne punkty P ₀ i P ₁ , liniowa krzywa Béziera jest po prostu linią między tymi dwoma punktami. Krzywa jest dana przez

${\ Displaystyle \ mathbf {B} (t) = \ mathbf {P} _ {0} + t (\ mathbf {P} _ {1} - \ mathbf {P} _ {0}) = (1-t) \mathbf {P} _{0}+t\mathbf {P} _{1},\ 0\równoważnik t\równik 1}$

i jest równoważne z interpolacją liniową .

Kwadratowe krzywe Béziera

Kwadratowe Béziera w sztuce smyczkowej : Punkty końcowe ( • ) i punkt kontrolny ( × ) definiują kwadratową krzywą Béziera ( ⋯ ).

Kwadratowa krzywa Béziera to ścieżka wyznaczona przez funkcję B ( t ), przy danych punktach P ₀ , P ₁ i P ₂ ,

${\ Displaystyle \ mathbf {B} (t) = (1-t) [(1-t) \ mathbf {P} _ {0} + t \ mathbf {P} _ {1}] + t [(1- t)\mathbf {P} _{1}+t\mathbf {P} _{2}],\ 0\równik t\równik 1}$,

co można interpretować jako liniową interpolantę odpowiednich punktów na liniowych krzywych Béziera odpowiednio od P ₀ do P ₁ i od P ₁ do P ₂ . Przekształcenie poprzedniego równania daje:

${\ Displaystyle \ mathbf {B} (t) = (1-t) ^ {2} \ mathbf {P} _ {0} + 2 (1-t) t \ mathbf {P} _ {1} + t ^ {2}\mathbf {P} _{2},\ 0\równik t\równik 1.}$

Można to zapisać w sposób podkreślający symetrię względem P ₁ :

${\ Displaystyle \ mathbf {B} (t) = \ mathbf {P} _ {1} + (1-t) ^ {2} (\ mathbf {P} _ {0} - \ mathbf {P} _ {1 })+t^{2}(\mathbf {P} _{2}-\mathbf {P} _{1}),\ 0\równoważnik t\równik 1.}$

Co natychmiast daje pochodną krzywej Béziera względem t :

${\ Displaystyle \ mathbf {B} '(t) = 2 (1-t) (\ mathbf {P} _ {1} - \ mathbf {P} _ {0}) + 2t (\ mathbf {P} _ { 2}-\mathbf {P} _ {1}),}$

z czego można wywnioskować, że styczne do krzywej w P ₀ i P ₂ przecinają się w P ₁ . Gdy t wzrasta od 0 do 1, krzywa oddala się od _{P0 w} kierunku _P1 , następnie zagina się, aby dojść do P2 z kierunku _P1 .

Druga pochodna krzywej Béziera względem t wynosi

${\ Displaystyle \ mathbf {B} '' (t) = 2 (\ mathbf {P} _ {2} -2 \ mathbf {P} _ {1} + \ mathbf {P} _ {0}).}$

Sześcienne krzywe Béziera

Cztery punkty P ₀ , P ₁ , P ₂ i P ₃ na płaszczyźnie lub w przestrzeni wielowymiarowej definiują sześcienną krzywą Béziera. Krzywa zaczyna się w punkcie P0 i biegnie _w kierunku punktu P1 i dochodzi do punktu _{P3 wychodząc} z kierunku P2 _. Zwykle nie przechodzi przez P ₁ lub P ₂ ; punkty te służą jedynie do dostarczania informacji kierunkowych. Odległość między P1 i P2 określa „jak daleko” i „jak szybko” krzywa przesuwa się w kierunku _P1 przed skrętem _w kierunku _{P2 .}

Zapisując B _{P i , P j , P k} ( t ) dla kwadratowej krzywej Béziera określonej przez punkty P _i , P _j i P _k , sześcienną krzywą Béziera można zdefiniować jako afiniczną kombinację dwóch kwadratowych krzywych Béziera:

${\ Displaystyle \ mathbf {B} (t) = (1-t) \ mathbf {B} _ {\ mathbf {P} _ {0}, \ mathbf {P} _ {1}, \ mathbf {P} _ {2}}(t)+t\mathbf {B} _{\mathbf {P} _{1},\mathbf {P} _{2},\mathbf {P} _{3}}(t), \ 0\równik t\równik 1.}$

Jawna postać krzywej to:

${\ Displaystyle \ mathbf {B} (t) = (1-t) ^ {3} \ mathbf {P} _ {0} + 3 (1-t) ^ {2} t \ mathbf {P} _ {1 }+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3},\ 0\równoważnik t\równik 1.}$

W przypadku niektórych opcji P ₁ i P ₂ krzywa może się przecinać lub zawierać wierzchołek .

Dowolną serię 4 różnych punktów można przekształcić w sześcienną krzywą Béziera, która przechodzi przez wszystkie 4 punkty w kolejności. Biorąc pod uwagę punkt początkowy i końcowy pewnej sześciennej krzywej Béziera oraz punkty wzdłuż krzywej odpowiadające t  = 1/3 i t  = 2/3, można odzyskać punkty kontrolne dla oryginalnej krzywej Béziera.

Pochodna sześciennej krzywej Béziera względem t wynosi

${\ Displaystyle \ mathbf {B} '(t) = 3 (1-t) ^ {2} (\ mathbf {P} _ {1} - \ mathbf {P} _ {0}) + 6 (1-t )t(\mathbf {P} _{2}-\mathbf {P} _{1})+3t^{2}(\mathbf {P} _{3}-\mathbf {P} _{2}) \,.}$

Druga pochodna krzywej Béziera względem t wynosi

${\ Displaystyle \ mathbf {B} '' (t) = 6 (1-t) (\ mathbf {P} _ {2} -2 \ mathbf {P} _ {1} + \ mathbf {P} _ {0 })+6t(\mathbf {P} _{3}-2\mathbf {P} _{2}+\mathbf {P} _{1})\,.}$

Ogólna definicja

Krzywe Béziera można zdefiniować dla dowolnego stopnia n .

Definicja rekurencyjna

Rekurencyjna definicja krzywej Béziera stopnia n wyraża ją jako kombinację liniową punkt-punkt ( interpolacja liniowa ) pary odpowiednich punktów na dwóch krzywych Béziera stopnia n  - 1.

Oznaczmy krzywą Béziera wyznaczoną przez dowolny wybór punktów P ₀ , P ₁ , ...,  P _k . Następnie, aby rozpocząć, ${\ Displaystyle \ mathbf {B} _ {\ mathbf {P} _ {0} \ mathbf {P} _ {1} \ ldots \ mathbf {P} _ {k}}}$

${\ Displaystyle \ mathbf {B} _ {\ mathbf {P} _ {0}} (t) = \ mathbf {P} _ {0} {\ tekst {i}}}$

${\ Displaystyle \ mathbf {B} (t) = \ mathbf {B} _ {\ mathbf {P} _ {0} \ mathbf {P} _ {1} \ ldots \ mathbf {P} _ {n}} ( t)=(1-t)\mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n-1}}(t) +t\mathbf {B} _{\mathbf {P} _{1}\mathbf {P} _{2}\ldots \mathbf {P} _{n}}(t)}$

Ta rekurencja jest wyjaśniona na poniższych animacjach .

Wyraźna definicja

Wzór można wyrazić wprost w następujący sposób (gdzie t ⁰ i (1-t) ⁰ są przedłużane w sposób ciągły do ​​1 przez [0,1]):

${\ Displaystyle {\ rozpocząć {wyrównane} \ mathbf {B} (t) & = \ suma _ {i = 0} ^ {n} {n \ wybierz i} (1-t) ^ {ni} t ^ {i }\mathbf {P} _{i}\\&=(1-t)^{n}\mathbf {P} _{0}+{n \choose 1}(1-t)^{n-1} t\mathbf {P} _{1}+\cdots +{n \choose n-1}(1-t)t^{n-1}\mathbf {P} _{n-1}+t^{n }\mathbf {P} _{n},&&0\leqslant t\leqslant 1\end{wyrównane}}}$

gdzie są współczynniki dwumianowe . ${\ Displaystyle \ scriptstyle {n \ wybierz i}}$

Na przykład, gdy n  = 5:

${\ Displaystyle {\ rozpocząć {wyrównane} \ mathbf {B} (t) & = (1-t) ^ {5} \ mathbf {P} _ {0} + 5t (1-t) ^ {4} \ mathbf {P} _{1}+10t^{2}(1-t)^{3}\mathbf {P} _{2}+10t^{3}(1-t)^{2}\mathbf {P } _{3}+5t^{4}(1-t)\mathbf {P} _{4}+t^{5}\mathbf {P} _{5},&&0\leqslant t\leqslant 1.\ koniec {wyrównany}}}$

Terminologia

Z tymi parametrycznymi krzywymi związana jest pewna terminologia. Mamy

${\ Displaystyle \ mathbf {B} (t) = \ suma _ {i = 0} ^ {n} b_ {i, n} (t) \ mathbf {P} _ {i}, \ \ \ 0 \ równoważnik t \równik 1}$

gdzie wielomiany

${\ Displaystyle b_ {i, n} (t) = {n \ wybierz i} t ^ {i} (1-t) ^ {ni}, \ \ \ i = 0, \ ldots, n}$

są znane jako wielomiany bazowe Bernsteina stopnia n .

Zauważ, że t ⁰  = 1, (1 −  t ) ⁰  = 1 i że współczynnik dwumianowy , , wynosi: ${\ Displaystyle \ scriptstyle {n \ wybierz i}}$

${\ Displaystyle {n \ wybierz i} = {\ Frac {n!} {i! (ni)!}}.}$

Punkty P _i nazywane są punktami kontrolnymi krzywej Béziera. Wielokąt utworzony przez połączenie punktów Béziera liniami , zaczynając od P ₀ i kończąc na P _n , nazywany jest wielokątem Béziera (lub wielokątem kontrolnym ). Wypukły kadłub wielokąta Béziera zawiera krzywą Béziera .

Forma wielomianowa

Czasami pożądane jest wyrażenie krzywej Béziera jako wielomianu zamiast sumy mniej prostych wielomianów Bernsteina . Zastosowanie twierdzenia o dwumianach do definicji krzywej, po którym nastąpi pewne przegrupowanie, przyniesie rezultaty

${\ Displaystyle \ mathbf {B} (t) = \ suma _ {j = 0} ^ {n} {t ^ {j} \ mathbf {C} _ {j}}}$

gdzie

${\ Displaystyle \ mathbf {C} _ {j} = {\ Frac {n!} {(nj)!}} \ suma _ {i = 0} ^ {j} {\ Frac {(-1) ^ {i +j}\mathbf {P} _{i}}{i!(ji)!}}=\prod _{m=0}^{j-1}(nm)\suma _{i=0}^{ j}{\frac {(-1)^{i+j}\mathbf {P} _{i}}{i!(ji)!}}.}$

Może to być praktyczne, jeśli można je obliczyć przed wieloma ocenami ; należy jednak zachować ostrożność, ponieważ krzywe wysokiego rzędu mogą nie być stabilne numerycznie ( w takim przypadku należy zastosować algorytm de Casteljau ). Zauważ, że pustym produktem jest 1. ${\ Displaystyle \ mathbf {C} _ {j}}$${\ Displaystyle \ mathbf {B} (t)}$

Nieruchomości

Sześcienna krzywa Béziera (żółta) może być identyczna z kwadratową (czarną) przez

1. kopiowanie punktów końcowych i

2. umieszczenie jej 2 środkowych punktów kontrolnych (żółte kółka) 2/3 wzdłuż odcinków linii od punktów końcowych do środkowego punktu kontrolnego krzywej kwadratowej (czarny prostokąt).

• Krzywa zaczyna się w P0 _i kończy w _Pn ; jest to tak zwana właściwość interpolacji punktu końcowego .
• Krzywa jest linią wtedy i tylko wtedy, gdy wszystkie punkty kontrolne są współliniowe .
• Początek i koniec krzywej są styczne odpowiednio do pierwszej i ostatniej sekcji wielokąta Béziera.
• Krzywą można podzielić w dowolnym punkcie na dwie krzywe podrzędne lub na dowolną liczbę krzywych podrzędnych, z których każda jest również krzywą Béziera.
• Niektóre krzywe, które wydają się proste, takie jak okrąg , nie mogą być dokładnie opisane za pomocą krzywej Béziera lub częściowej krzywej Béziera; chociaż czteroczęściowa sześcienna krzywa Béziera może przybliżać okrąg (patrz złożona krzywa Béziera ), z maksymalnym błędem promieniowym mniejszym niż jedna część na tysiąc, gdy każdy wewnętrzny punkt kontrolny (lub punkt offline) jest odległością poziomą lub pionową od zewnętrzny punkt kontrolny na okręgu jednostkowym. Mówiąc bardziej ogólnie, n - częściowa sześcienna krzywa Béziera może przybliżać okrąg, gdy każdy wewnętrzny punkt kontrolny jest odległością od zewnętrznego punktu kontrolnego na okręgu jednostkowym, gdzie t wynosi 360/ n stopni, a n > 2.${\ Displaystyle \ textstyle {\ Frac {4 \ lewo ({\ sqrt {2}} -1 \ prawo)} {3}}}$${\ Displaystyle \ textstyle {\ Frac {4} {3}} \ tan (t / 4)}$
• Każda kwadratowa krzywa Béziera jest również sześcienną krzywą Béziera, a bardziej ogólnie, każda krzywa Béziera stopnia n jest również krzywą stopnia m dla dowolnego m > n . Bardziej szczegółowo, krzywa stopnia n z punktami kontrolnymi P ₀ , ..., P _n jest równoważna (włączając parametryzację) krzywej stopnia n + 1 z punktami kontrolnymi P' ₀ , ..., P' _{n + 1} , gdzie .${\ Displaystyle \ mathbf {P} '_ {k} = {\ tfrac {k} {n + 1}} \ mathbf {P} _ {k-1} + \ lewo (1- {\ tfrac {k} n+1}}\right)\mathbf {P} _{k}}$
• Krzywe Béziera mają właściwość zmniejszania zmienności . Intuicyjnie oznacza to, że krzywa Béziera nie „faluje” bardziej niż wielokąt jej punktów kontrolnych i może faktycznie „falować” mniej.
• Nie ma lokalnej kontroli na krzywych Béziera stopnia n - co oznacza, że ​​jakakolwiek zmiana punktu kontrolnego wymaga ponownego obliczenia, a tym samym wpływa na aspekt całej krzywej, „chociaż im dalej jest od punktu kontrolnego, który został zmieniony, tym mniejszy jest zmiana krzywej”.
• Krzywa Béziera rzędu wyższego niż dwa może przecinać się lub mieć wierzchołek dla pewnych wyborów punktów kontrolnych.

Krzywa drugiego rzędu to odcinek paraboliczny

Równoważność kwadratowej krzywej Béziera i odcinka parabolicznego

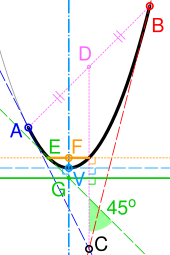
Kwadratowa krzywa Béziera jest również odcinkiem paraboli . Ponieważ parabola jest przekrojem stożkowym , niektóre źródła określają kwadratowy Béziers jako „łuki stożkowe”. W odniesieniu do rysunku po prawej stronie, ważne cechy paraboli można wyprowadzić w następujący sposób:

1. Styczne do paraboli w punktach końcowych krzywej (A i B) przecinają się w jej punkcie kontrolnym (C).
2. Jeśli D jest środkiem AB, styczna do krzywej prostopadłej do CD (przerywana linia cyjanowa) wyznacza jej wierzchołek (V). Jego oś symetrii (kreska-kropka cyjan) przechodzi przez V i jest prostopadła do stycznej.
3. E jest albo punktem na krzywej ze styczną pod kątem 45° do CD (przerywana zielona linia). Jeśli G jest przecięciem tej stycznej i osi, linia przechodząca przez G i prostopadła do CD jest kierownicą (ciągłe zielone).
4. Ognisko (F) znajduje się na przecięciu osi i linii przechodzącej przez E i prostopadłej do CD (żółta kropkowana). Latus rectum to odcinek linii w obrębie krzywej (stały żółty).

Pochodna

Pochodna krzywej rzędu n wynosi

${\ Displaystyle \ mathbf {B} '(t) = n \ suma _ {i = 0} ^ {n-1} b_ {i, n-1} (t) (\ mathbf {P} _ {i + 1 }-\mathbf {P} _ {i}).}$

Konstruowanie krzywych Béziera

Krzywe liniowe

t w funkcji liniowej krzywej Béziera można traktować jako opisujące odległość B ( t ) od P ₀ do P ₁ . Na przykład, gdy t = 0,25, B ( t ) to jedna czwarta drogi od punktu P ₀ do P ₁ . Ponieważ t zmienia się od 0 do 1, _{B (} t ) opisuje linię od P0 do P1 .

Animacja liniowej krzywej Béziera, t w [0,1]

Krzywe kwadratowe

Dla kwadratowych krzywych Béziera można skonstruować punkty pośrednie Q ₀ i Q ₁ takie, że gdy t zmienia się od 0 do 1:

• Punkt Q ₀ ( t ) zmienia się od P ₀ do P ₁ i opisuje liniową krzywą Béziera.
• Punkt Q1 ( _t ) zmienia się od P1 do _P2 i _opisuje liniową krzywą Béziera .
• Punkt B ( t ) jest interpolowany liniowo między Q0 ( t ) a Q1 ₍ t ₎ i opisuje kwadratową krzywą Béziera.

Konstrukcja kwadratowej krzywej Béziera		Animacja kwadratowej krzywej Béziera, t w [0,1]

Krzywe wyższego rzędu

Dla krzywych wyższego rzędu potrzeba odpowiednio więcej punktów pośrednich. Dla krzywych sześciennych można skonstruować punkty pośrednie Q ₀ , Q ₁ i Q ₂ opisujące liniowe krzywe Béziera oraz punkty R ₀ i R ₁ opisujące kwadratowe krzywe Béziera:

Budowa sześciennej krzywej Béziera		Animacja sześciennej krzywej Béziera, t w [0,1]

Dla krzywych czwartego rzędu można skonstruować punkty pośrednie Q ₀ , Q ₁ , Q ₂ i Q ₃ opisujące liniowe krzywe Béziera, punkty R ₀ , R ₁ i R ₂ opisujące kwadratowe krzywe Béziera oraz punkty S ₀ i S ₁ , które opisz sześcienne krzywe Béziera:

Konstrukcja kwartalnej krzywej Béziera		Animacja kwartalnej krzywej Béziera, t w [0,1]

W przypadku krzywych piątego rzędu można skonstruować podobne punkty pośrednie.

Animacja krzywej Béziera piątego rzędu, t w [0,1] na czerwono. Pokazane są również krzywe Béziera dla każdego z niższych rzędów.

Te reprezentacje opierają się na procesie stosowanym w algorytmie De Casteljau do obliczania krzywych Béziera.

Przesunięcia (lub obrysowanie) krzywych Béziera

Krzywa ze stałym przesunięciem od danej krzywej Béziera, zwana w matematyce krzywą przesuniętą lub równoległą (leżąca „równolegle” do pierwotnej krzywej, jak przesunięcie między szynami na torze kolejowym ), nie może być dokładnie utworzona przez krzywą Béziera ( z wyjątkiem kilku błahych przypadków). Ogólnie rzecz biorąc, dwustronna krzywa przesunięcia sześciennej krzywej Béziera jest krzywą algebraiczną 10. rzędu, a bardziej ogólnie dla Béziera stopnia n dwustronna krzywa przesunięcia jest krzywą algebraiczną stopnia 4 n -2. Istnieją jednak metody heurystyczne , które zwykle dają odpowiednie przybliżenie do celów praktycznych.

W dziedzinie grafiki wektorowej malowanie dwóch symetrycznie oddalonych od siebie krzywych offsetowych nazywa się głaskaniem (krzywa Béziera lub ogólnie ścieżka kilku segmentów Béziera). Konwersja z przesuniętych krzywych do wypełnionych konturów Béziera ma praktyczne znaczenie przy konwersji czcionek zdefiniowanych w Metafont , które wymagają obrysowywania krzywych Béziera, na szerzej stosowane czcionki PostScript typu 1 , które wymagają jedynie (ze względu na wydajność) matematycznie prostszej operacji wypełnienie konturu zdefiniowanego przez (nieprzecinające się) krzywe Béziera.

Podniesienie stopnia

Krzywą Béziera stopnia n można przekształcić w krzywą Béziera stopnia n  + 1 o tym samym kształcie . Jest to przydatne, jeśli oprogramowanie obsługuje krzywe Béziera tylko o określonym stopniu. Na przykład systemy, które mogą pracować tylko z sześciennymi krzywymi Béziera, mogą domyślnie pracować z krzywymi kwadratowymi, używając ich równoważnej reprezentacji sześciennej.

Aby wykonać elewację stopnia, używamy równości Każdy składnik jest mnożony przez (1 −  t ) i  t , zwiększając w ten sposób stopień o jeden bez zmiany wartości. Oto przykład zwiększania stopnia od 2 do 3. ${\ Displaystyle \ mathbf {B} (t) = (1-t) \ mathbf {B} (t) + t \ mathbf {B} (t).}$${\ Displaystyle \ mathbf {b} _ {i, n} (t) \ mathbf {P} _ {i}}$

${\ Displaystyle {\ rozpocząć {wyrównane} (1-t) ^ {2} \ mathbf {P} _ {0} + 2 (1-t) t \ mathbf {P} _ {1} + t ^ {2} \mathbf {P} _{2}&=(1-t)^{3}\mathbf {P} _{0}+2(1-t)^{2}t\mathbf {P} _{1} +(1-t)t^{2}\mathbf {P} _{2}+(1-t)^{2}t\mathbf {P} _{0}+2(1-t)t^{ 2}\mathbf {P} _{1}+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+( 1-t)^{2}t\lewo(\mathbf {P} _{0}+2\mathbf {P} _{1}\prawo)+(1-t)t^{2}\lewo(2 \mathbf {P} _{1}+\mathbf {P} _{2}\right)+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3} \mathbf {P} _{0}+3(1-t)^{2}t{\tfrac {1}{3}}\left(\mathbf {P} _{0}+2\mathbf {P} _{1}\right)+3(1-t)t^{2}{\tfrac {1}{3}}\left(2\mathbf {P} _{1}+\mathbf {P} _{ 2}\right)+t^{3}\mathbf {P} _{2}\end{wyrównane}}}$

Dla dowolnego n używamy równości

${\ Displaystyle {\ rozpocząć {przypadki} {n + 1 \ wybierz i} (1-t) \ mathbf {b} _ {i, n} = {n \ wybierz i} \ mathbf {b} _ {i, n +1}\\{n+1 \wybierz i+1}t\mathbf {b} _{i,n}={n \wybierz i}\mathbf {b} _{i+1,n+1}\ end{przypadki}}\quad \implikuje \quad {\begin{przypadki}(1-t)\mathbf {b} _{i,n}={\frac {n+1-i}{n+1}} \mathbf {b} _{i,n+1}\\t\mathbf {b} _{i,n}={\frac {i+1}{n+1}}\mathbf {b} _{i +1,n+1}\end{przypadki}}}$

W związku z tym:

${\ Displaystyle {\ rozpocząć {wyrównane} \ mathbf {B} (t) & = (1-t) \ suma _ {i = 0} ^ {n} \ mathbf {b} _ {i, n} (t) \mathbf {P} _{i}+t\suma _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}\\&= \sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}(t)\mathbf {P} _ {i}+\sum _{i=0}^{n}{\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}(t)\mathbf {P} _{i}\\&=\suma _{i=0}^{n+1}\left({\frac {i}{n+1}}\mathbf {P} _{i-1 }+{\frac {n+1-i}{n+1}}\mathbf {P} _{i}\right)\mathbf {b} _{i,n+1}(t)\\&= \sum _{i=0}^{n+1}\mathbf {b} _{i,n+1}(t)\mathbf {P'} _{i}\end{wyrównane}}}$

wprowadzanie arbitralne i . ${\ Displaystyle \ mathbf {P} _ {-1}}$${\ Displaystyle \ mathbf {P} _ {n + 1}}$

Dlatego nowe punkty kontrolne są

${\ Displaystyle \ mathbf {P '} _ {i} = {\ Frac {i} {n + 1}} \ mathbf {P} _ {i-1} + {\ Frac {n + 1-i} {n +1}}\mathbf {P} _{i},\quad i=0,\ldots,n+1.}$

Powtarzające się podwyższenie stopnia

Koncepcję wysokości stopnia można powtórzyć na wielokącie kontrolnym R , aby uzyskać sekwencję wielokątów kontrolnych R , R ₁ , R ₂ i tak dalej. Po podniesieniu o r stopni wielokąt R _r ma wierzchołki P _{0, r} , P _{1, r} , P _{2, r} , ..., P _{n + r , r} dane przez

${\ Displaystyle \ mathbf {P} _ {i, r} = \ suma _ {j = 0} ^ {n} \ mathbf {P} _ {j} {\ tbinom {n} {j}} {\ frac { \tbinom {r}{ij}}{\tbinom {n+r}{i}}}.}$

Można również pokazać, że dla podstawowej krzywej Béziera B ,

${\ Displaystyle \ mathbf {\ lim _ {r \ do \ infty} R_ {r}} = \ mathbf {B}.}$

Racjonalne krzywe Béziera

Segmenty przekrojów stożkowych reprezentowane dokładnie przez wymierne krzywe Béziera

Racjonalna krzywa Béziera dodaje regulowane wagi, aby zapewnić bliższe przybliżenie dowolnych kształtów. Licznik jest ważoną krzywą Béziera w postaci Bernsteina, a mianownik jest ważoną sumą wielomianów Bernsteina . Wymierne krzywe Béziera mogą, między innymi, służyć do dokładnego przedstawiania segmentów przekrojów stożkowych , w tym łuków kołowych.

Biorąc pod uwagę n  + 1 punktów kontrolnych P ₀ , ..., P _n , wymierną krzywą Béziera można opisać wzorem

${\ Displaystyle \ mathbf {B} (t) = {\ Frac {\ suma _ {i = 0} ^ {n} b_ {i, n} (t) \ mathbf {P} _ {i} w_ {i} }{\suma _{i=0}^{n}b_{i,n}(t)w_{i}}},}$

lub po prostu

${\ Displaystyle \ mathbf {B} (t) = {\ Frac {\ suma _ {i = 0} ^ {n} {n \ wybierz i} t ^ {i} (1-t) ^ {ni} \ mathbf {P} _{i}w_{i}}{\sum _{i=0}^{n}{n \wybierz i}t^{i}(1-t)^{ni}w_{i}} }.}$

Wyrażenie można rozszerzyć, używając systemów liczbowych oprócz liczb rzeczywistych dla wag. Na płaszczyźnie zespolonej punkty {1}, {-1} i {1} o wagach { }, {1} i { } generują pełny okrąg o promieniu jeden. W przypadku krzywych z punktami i wagami na okręgu wagi można skalować bez zmiany kształtu krzywej. Skalowanie centralnej wagi powyższej krzywej o 1,35508 daje bardziej jednolitą parametryzację. ${\ styl wyświetlania ja}$${\ Displaystyle -i}$

Aplikacje

Grafika komputerowa

Ścieżka Béziera w programie Adobe Illustrator

Krzywe Béziera są szeroko stosowane w grafice komputerowej do modelowania gładkich krzywych. Ponieważ krzywa jest całkowicie zawarta w wypukłej otoczce jej punktów kontrolnych , punkty te można wyświetlać graficznie i wykorzystywać do intuicyjnego manipulowania krzywą. Transformacje afiniczne , takie jak translacja i obrót , można zastosować na krzywej, stosując odpowiednią transformację w punktach kontrolnych krzywej.

Najczęściej spotykane są kwadratowe i sześcienne krzywe Béziera. Krzywe wyższego stopnia są bardziej kosztowne obliczeniowo do oceny. Gdy potrzebne są bardziej złożone kształty, krzywe Béziera niższego rzędu są łączone razem, tworząc złożoną krzywą Béziera . Złożona krzywa Béziera jest powszechnie określana jako „ścieżka” w językach grafiki wektorowej (takich jak PostScript ), standardach grafiki wektorowej (takich jak SVG ) i programach do grafiki wektorowej (takich jak Artline , Timeworks Publisher , Adobe Illustrator , CorelDraw , Inkscape i Allegro ) . Aby połączyć krzywe Béziera w złożoną krzywą Béziera bez załamań, właściwość zwaną G1 continuous , wystarczy wymusić, aby punkt kontrolny, w którym spotykają się dwie składowe krzywe Béziera, leżał na linii wyznaczonej przez dwa punkty kontrolne po obu stronach.

Abstrakcyjna kompozycja sześciennych krzywych Béziera ze śledzeniem promieni w 3D. Przecięcie promienia z objętościami przesuniętymi wzdłuż krzywych jest obliczane za pomocą algorytmu Phantom Ray-Hair Intersector.

Najprostszą metodą konwersji skanowania ( rasteryzacji ) krzywej Béziera jest ocena jej w wielu blisko rozmieszczonych punktach i konwersja skanowania przybliżonej sekwencji segmentów linii. Nie gwarantuje to jednak, że zrasteryzowane dane wyjściowe będą wyglądać wystarczająco gładko, ponieważ punkty mogą być rozmieszczone zbyt daleko od siebie. I odwrotnie, może generować zbyt wiele punktów w obszarach, w których krzywa jest zbliżona do liniowej. Powszechną metodą adaptacyjną jest podział rekurencyjny, w którym punkty kontrolne krzywej są sprawdzane, aby zobaczyć, czy krzywa zbliża się do linii z niewielką tolerancją. Jeśli nie, krzywa jest dzielona parametrycznie na dwa segmenty, 0 ≤ t ≤ 0,5 i 0,5 ≤ t ≤ 1, i ta sama procedura jest stosowana rekurencyjnie do każdej połowy. Istnieją również metody różnicowania w przód, ale należy zwrócić szczególną uwagę na analizę propagacji błędów.

Metody analityczne, w których Béziera przecina się z każdą linią skanowania, obejmują znajdowanie pierwiastków wielomianów sześciennych (dla sześciennych Béziera) i radzenie sobie z wieloma pierwiastkami, więc nie są one często używane w praktyce.

Algorytm rasteryzacji zastosowany w Metafont opiera się na dyskretyzacji krzywej, tak że jest ona aproksymowana przez sekwencję „ ruchów wieży ”, które są czysto pionowe lub czysto poziome, wzdłuż granic pikseli. W tym celu płaszczyzna jest najpierw dzielona na osiem sektorów 45 ° (przez osie współrzędnych i dwie linie ), następnie krzywa jest rozkładana na mniejsze segmenty, tak że kierunek segmentu krzywej pozostaje w jednym sektorze; ponieważ prędkość na krzywej jest wielomianem drugiego stopnia, znalezienie wartości, w których jest równoległa do jednej z tych prostych, można wykonać, rozwiązując równania kwadratowe . W każdym segmencie dominuje ruch poziomy lub pionowy, a całkowitą liczbę kroków w dowolnym kierunku można odczytać ze współrzędnych punktu końcowego; na przykład dominuje poziomy ruch sektora 0–45 ° w prawo, więc pozostaje tylko zdecydować, między którymi krokami w prawo krzywa powinna wzrosnąć. ${\ displaystyle y = \ pm x}$${\ Displaystyle t}$

Istnieje również zmodyfikowana postać krzywej algorytmu rysowania linii Bresenhama autorstwa Zingla, która wykonuje tę rasteryzację, dzieląc krzywą na wymierne części i obliczając błąd w każdym położeniu piksela tak, że porusza się on pod kątem 45 ° lub prosto, w zależności od błędu złożonego jako iteruje po krzywej. Zmniejsza to obliczenia następnego kroku do serii dodawania i odejmowania liczb całkowitych .

Animacja

W aplikacjach do animacji, takich jak Adobe Flash i Synfig , krzywe Béziera są używane na przykład do konturowania ruchu. Użytkownicy wyznaczają żądaną ścieżkę na krzywych Béziera, a aplikacja tworzy potrzebne ramki, aby obiekt poruszał się po ścieżce.

W animacji 3D krzywe Béziera są często używane do definiowania ścieżek 3D, a także krzywe 2D do interpolacji klatek kluczowych. Krzywe Béziera są obecnie bardzo często używane do kontrolowania wygładzania animacji w CSS , JavaScript , JavaFx i Flutter SDK .

Czcionki

Czcionki TrueType wykorzystują złożone krzywe Béziera złożone z kwadratowych krzywych Béziera. Inne języki i narzędzia do tworzenia obrazów (takie jak PostScript , Asymptote , Metafont i SVG ) używają złożonych Béziera składających się z sześciennych krzywych Béziera do rysowania zakrzywionych kształtów. Czcionki OpenType mogą wykorzystywać dowolny rodzaj krzywej, w zależności od technologii czcionek leżącej u podstaw opakowania OpenType.

Wewnętrzne renderowanie wszystkich krzywych Béziera w rendererach czcionek lub grafiki wektorowej podzieli je rekurencyjnie do punktu, w którym krzywa jest wystarczająco płaska, aby można ją było narysować jako serię segmentów liniowych lub kołowych. Dokładny algorytm podziału zależy od implementacji, należy przestrzegać jedynie kryteriów płaskości, aby osiągnąć niezbędną precyzję i uniknąć niemonotonicznych lokalnych zmian krzywizny. Funkcja „gładkiej krzywej” wykresów w programie Microsoft Excel również wykorzystuje ten algorytm.

Ponieważ łuki okręgów i elips nie mogą być dokładnie reprezentowane przez krzywe Béziera, są one najpierw przybliżane przez krzywe Béziera, które z kolei są przybliżane przez łuki okręgów. Jest to nieefektywne, ponieważ istnieją również przybliżenia wszystkich krzywych Béziera za pomocą łuków okręgów lub elips, które można renderować przyrostowo z dowolną precyzją. Inne podejście, stosowane przez nowoczesne sprzętowe karty graficzne z przyspieszoną geometrią, może konwertować dokładnie wszystkie krzywe Béziera i stożkowe (lub powierzchnie) na NURBS , które można renderować przyrostowo bez uprzedniego rekurencyjnego dzielenia krzywej w celu osiągnięcia wymaganego warunku płaskości. Takie podejście zachowuje również definicję krzywej we wszystkich liniowych lub perspektywicznych przekształceniach i projekcjach 2D i 3D.

Silniki czcionek, takie jak FreeType , rysują krzywe (i linie) czcionki na pikselowanej powierzchni za pomocą procesu znanego jako rasteryzacja czcionki .

Robotyka

Krzywe Béziera mogą być wykorzystywane w robotyce do tworzenia trajektorii efektora końcowego ze względu na zdolność wielokąta kontrolnego do wyraźnego wskazania, czy ścieżka koliduje z pobliską przeszkodą lub obiektem. Ponadto trajektorie przestrzeni stawowej można dokładnie rozróżnić za pomocą krzywych Béziera. W związku z tym pochodne trajektorii przestrzennych przegubów są wykorzystywane do obliczania dynamiki i wysiłku sterowania (profile momentu obrotowego) manipulatora robota.

Zobacz też

• Powierzchnia Béziera
• B-splajn
• Klejnot/4 i Klejnot/5
• Krzywa Hermite'a
• NURBS
• Sztuka smyczkowa - krzywe Béziera są również tworzone przez wiele popularnych form sztuki smyczkowej, w których struny są zapętlone na ramie z gwoździ.
• Właściwość zmniejszania zmienności krzywych Béziera

Notatki

Bibliografia

Cytaty

Źródła

Dalsza lektura

• A Primer on Bézier Curves  - internetowa książka open source wyjaśniająca krzywe Béziera i powiązane algorytmy graficzne, z interaktywną grafiką
• Cubic Bezier Curves — Under the Hood (wideo)  — wideo pokazujące, jak komputery renderują sześcienną krzywą Béziera, autorstwa Petera Nowella
• Kolumna fabularna Od Béziera do Bernsteina z American Mathematical Society
• „Krzywa Béziera” , Encyklopedia matematyki , EMS Press , 2001 [1994]
• Prautzsch, Hartmut; Boehm, Wolfgang; Paluszny, Marco (2002). Techniki Béziera i B-Spline . Springer Science & Business Media. ISBN 978-3-540-43761-1.
• Gallier, Jean (1999). „Rozdział 5. Krzywe wielomianowe jako krzywe Béziera” . Krzywe i powierzchnie w modelowaniu geometrycznym: teoria i algorytmy . Morgana Kaufmanna.Ta książka jest wyczerpana i dostępna bezpłatnie u autora.
• Farin, Gerald E. (2002). Krzywe i powierzchnie dla CAGD: praktyczny przewodnik (wyd. 5). Morgana Kaufmanna. ISBN 978-1-55860-737-8.
• Weisstein, Eric W. „Krzywa Beziera” . MathWorld .
• Hoffmann, Gernot. „Krzywe Beziera” (PDF) . Zarchiwizowane od oryginału (PDF) w dniu 2006-12-02.(60 stron)
• Ahn, Młody Joon (2004). „Aproksymacja łuków kołowych i krzywych przesuniętych za pomocą krzywych Béziera wysokiego stopnia” . Journal of Computational and Applied Mathematics . 167 (2): 405–416. Bibcode : 2004JCoAM.167..405A . doi : 10.1016/j.cam.2003.10.008 .
• Davies, Jason. „Animowane krzywe Béziera” .
• Hovey, Czad (20 maja 2022). „Geometria Béziera” . GitHub .
• Hovey, Czad (2022). Sformułowanie i implementacja w Pythonie geometrii Béziera i B-splajnu. Piasek2022-7702C . (153 strony)

Zewnętrzne linki

Kod komputerowy

• TinySpline: otwarta biblioteka C dla NURBS, B-splajnów i krzywych Béziera z powiązaniami dla różnych języków
• Biblioteka C++ do generowania funkcji Béziera w czasie kompilacji
• Prosta implementacja krzywej Béziera za pomocą metody rekurencyjnej w Pythonie