Kropka - Cograph

Wykres turan T (13,4), przykładem kograf

W teorii wykres , na kograf lub dopełniacza redukowalnych wykresu lub P ₄ -FREE wykresie , to wykres , który można wytwarzać z jednego wierzchołka wykres K ₁ poprzez komplementację , a suma rozłączna . Oznacza to, że rodzina grafów jest najmniejszą klasą grafów, która zawiera K ₁ i jest zamknięta na komplementację i sumę rozłączną.

Kopografy zostały odkryte niezależnie przez kilku autorów od lat siedemdziesiątych; wczesne odniesienia obejmują Junga (1978) , Lerchsa (1971) , Seinsche (1974) i Sumnera (1974) . Nazywano je również D*-grafami , dziedzicznymi grafami Daceya (od pokrewnej pracy Jamesa C. Daceya Jr. na temat krat ortomodularnych ) i grafami 2-parzystości . Mają prosty rozkład strukturalny obejmujący operacje na grafach sumowania i uzupełniania, które mogą być zwięźle reprezentowane przez drzewo etykietowane i używane algorytmicznie do skutecznego rozwiązywania wielu problemów, takich jak znajdowanie maksymalnej kliki, która jest trudna w bardziej ogólnych klasach grafów.

Szczególne przypadki cographs zawierać graf pełny , kompletny graf dwudzielny , kasetowej wykresy i wykresy progowych . W cographs są z kolei szczególne przypadki wykresów na odległość dziedziczna , wykresy permutacji , wykresy porównywalność i graf doskonały .

Definicja

Konstrukcja rekurencyjna

Każdy wykres może być skonstruowany zgodnie z następującymi zasadami:

1. każdy pojedynczy graf wierzchołkowy jest cograph;
2. if jest cograph, więc jest jego grafem dopełnienia ;${\ Displaystyle G}$ ${\displaystyle {\overline {G}}}$
3. jeśli i są cographs, tak samo ich rozłączny związek .${\ Displaystyle G}$${\ Displaystyle H}$${\ Displaystyle G \ filiżanka H}$

Kografy można zdefiniować jako grafy, które można skonstruować za pomocą tych operacji, zaczynając od grafów jednowierzchołkowych. Alternatywnie, zamiast używać operacji dopełniania, można użyć operacji join, która polega na utworzeniu sumy rozłącznej, a następnie dodaniu krawędzi między każdą parą wierzchołka z i wierzchołka z . ${\ Displaystyle G \ filiżanka H}$${\ Displaystyle G}$${\ Displaystyle H}$

Inne charakterystyki

Można podać kilka alternatywnych charakterystyk wykresów. Pomiędzy nimi:

• Krzywa to wykres, który nie zawiera ścieżki P ₄ na 4 wierzchołkach (a więc o długości 3) jako podgraf indukowany . Oznacza to, że graf jest kografem wtedy i tylko wtedy, gdy dla dowolnych czterech wierzchołków , jeżeli i są krawędziami grafu, to co najmniej jeden z lub jest również krawędzią.${\displaystyle v_{1},v_{2},v_{3},v_{4}}$${\displaystyle \{v_{1},v_{2}\},\{v_{2},v_{3}\}}$${\displaystyle \{v_{3},v_{4}\}}$${\displaystyle \{v_{1},v_{3}\},\{v_{1},v_{4}\}}$${\displaystyle \{v_{2},v_{4}\}}$
• Krzywa jest grafem, którego wszystkie indukowane podgrafy mają tę właściwość, że dowolna maksymalna klika przecina dowolny maksymalny niezależny zbiór w jednym wierzchołku.
• Krzywa to graf, w którym każdy nietrywialny podgraf indukowany ma co najmniej dwa wierzchołki o tym samym sąsiedztwie.
• Krzywa jest grafem, w którym każdy połączony podgraf indukowany ma rozłączne dopełnienie.
• Kopograf to wykres, którego wszystkie połączone indukowane podgrafy mają średnicę co najwyżej 2.
• Krzywa to wykres, w którym każda połączona składowa jest wykresem dziedzicznym odległości o średnicy co najwyżej 2.
• Wykres to wykres o szerokości kliki co najwyżej 2.
• Kograf jest wykresem porównywalność z szeregowo-równoległy porządek częściowy .
• Cograph to wykres permutacji dającej się oddzielić permutacji .
• Kograf to graf, którego minimalne uzupełnienia akordowe są grafami trywialnie doskonałymi .
• Krzywa to dziedzicznie dobrze pokolorowany wykres , taki, w którym każde zachłanne zabarwienie każdego indukowanego podwykresu wykorzystuje optymalną liczbę kolorów.
• Wykres jest kografem wtedy i tylko wtedy, gdy każdy porządek wierzchołków grafu jest porządkiem idealnym , ponieważ brak P ₄ oznacza, że ​​żadna przeszkoda dla porządku idealnego nie będzie istniała w żadnym porządku wierzchołków.

Cotrees

Cotree i odpowiedni kograf. Każda krawędź ( u , v ) w kografie ma kolor pasujący do najmniej wspólnego przodka u i v w cotree.

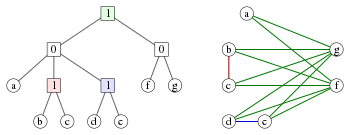
Cotree drzewo w którym węzły wewnętrzne są oznaczone liczbami 0 i 1. Każdy cotree T definiuje kograf G o liści T jako wierzchołki i w którym Poddrzewo zakorzenione w każdym węźle T odpowiada na indukowaną podgrafu w G określonym przez zbiór liści schodzących z tego węzła:

• Poddrzewo składające się z węzła pojedynczego liścia odpowiada indukowanemu podgrafowi z pojedynczym wierzchołkiem.
• Poddrzewo zakorzenione w węźle oznaczonym jako 0 odpowiada połączeniu podgrafów zdefiniowanych przez dzieci tego węzła.
• Poddrzewem zakorzenione w węźle oznaczonego jako 1 odnosi się do przyłączenia z subgraphs określonych przez dzieci tego węzła; to znaczy tworzymy unię i dodajemy krawędź między każdymi dwoma wierzchołkami odpowiadającymi liściom w różnych poddrzewach. Alternatywnie, złączenie zbioru wykresów może być postrzegane jako utworzone przez uzupełnienie każdego wykresu, utworzenie unii uzupełnień, a następnie uzupełnienie powstałej unii.

Równoważnym sposobem opisania kografu utworzonego z cotree jest to, że dwa wierzchołki są połączone krawędzią wtedy i tylko wtedy, gdy najniższy wspólny przodek odpowiednich liści jest oznaczony przez 1. I odwrotnie, każdy kograf może być reprezentowany w ten sposób przez cotree . Jeśli wymagamy, aby etykiety na dowolnej ścieżce liścia głównego tego drzewa zmieniały się między 0 a 1, ta reprezentacja jest unikalna.

Własności obliczeniowe

Wykresy mogą być rozpoznawane w czasie liniowym, a reprezentacja cotree może być skonstruowana przy użyciu dekompozycji modularnej , udoskonalenia podziału , LexBFS lub dekompozycji rozdzielonej . Po zbudowaniu reprezentacji cotree, wiele znanych problemów z wykresami można rozwiązać za pomocą prostych obliczeń oddolnych na cotrees.

Na przykład, aby znaleźć maksymalną klikę w kografie, oblicz w kolejności od dołu do góry maksymalną klikę w każdym podwykresie reprezentowanym przez poddrzewo cotree. Dla węzła oznaczonego jako 0, maksymalna klika jest maksymalną spośród klik obliczonych dla dzieci tego węzła. Dla węzła oznaczonego 1, maksymalna klika jest sumą klik obliczonych dla dzieci tego węzła i ma rozmiar równy sumie rozmiarów kliki dzieci. Tak więc, naprzemiennie maksymalizując i sumując wartości przechowywane w każdym węźle drzewa, możemy obliczyć maksymalny rozmiar kliki, a naprzemiennie maksymalizując i biorąc sumy, możemy skonstruować samą maksymalną klikę. Podobne obliczenia drzewa od dołu do góry pozwalają obliczyć maksymalny niezależny zbiór , liczbę kolorowania wierzchołków , maksymalne pokrycie kliki i hamiltoniczność (czyli istnienie cyklu hamiltonowskiego ) w czasie liniowym na podstawie reprezentacji cotree. Ponieważ kografy mają ograniczoną szerokość kliki, twierdzenie Courcelle'a może być użyte do testowania dowolnej właściwości w monadycznej logice drugiego rzędu grafów (MSO ₁ ) na kografach w czasie liniowym.

Problem sprawdzania, czy dany graf jest oddalony o k wierzchołków i/lub t krawędzi od cographu, jest możliwy do wykonania przy użyciu stałych parametrów . Rozstrzygnięcie, czy graf można usunąć k -krawędziowo do kografu, można rozwiązać w czasie O ^* (2.415 ^k ), a k -edytować krawędziowo do kografu w czasie O ^* (4.612 ^k ). Jeśli największy indukowany podwykres wykresu można znaleźć, usuwając z wykresu k wierzchołków, można go znaleźć w czasie O ^* (3,30 ^k ).

Dwa koparki są izomorficzne wtedy i tylko wtedy, gdy ich cotrees (w formie kanonicznej bez dwóch sąsiednich wierzchołków o tej samej etykiecie) są izomorficzne. Dzięki tej równoważności można określić w czasie liniowym, czy dwa wykresy są izomorficzne, konstruując ich cotrees i stosując test izomorfizmu w czasie liniowym dla drzew oznaczonych.

Jeśli H jest indukowanym podgrafem kopografu G , to samo H jest kografem; cotree dla H może być utworzony przez usunięcie niektórych liści z cotree dla G, a następnie usunięcie węzłów, które mają tylko jedno dziecko. Z twierdzenia Kruskala wynika, że relacja bycia podgrafem indukowanym jest dobrze quasi-uporządkowaniem na kografach. Tak więc, jeśli podrodzina kografów (taka jak kografy planarne ) jest zamknięta w ramach operacji na podgrafach indukowanych, to ma skończoną liczbę podgrafów indukowanych zabronionych . Obliczeniowo oznacza to, że testowanie przynależności do takiej podrodziny można przeprowadzić w czasie liniowym, wykorzystując obliczenia oddolne na drzewie danego grafu w celu sprawdzenia, czy zawiera on którykolwiek z tych zabronionych podgrafów. Jednakże, gdy rozmiary dwóch wykresów są zmienne, testowanie, czy jeden z nich jest indukowanym podgrafem drugiego, jest NP-zupełne .

Kografy odgrywają kluczową rolę w algorytmach rozpoznawania funkcji jednokrotnego odczytu .

Wyliczenie

Liczba połączonych wykresów o n wierzchołkach, dla n = 1, 2, 3, ..., wynosi:

1, 1, 2, 5, 12, 33, 90, 261, 766, 2312, 7068, 21965, 68954, ... (sekwencja A000669 w OEIS )

Dla n > 1 jest taka sama liczba niepołączonych kografów, ponieważ dla każdego kografu połączony jest dokładnie jeden z nich lub jego graf dopełnienia .

Powiązane rodziny wykresów

Podklasy

Każdy kompletny graf K _n jest kografem, którego drzewostan składa się z jednego węzła i n liści. Podobnie każdy kompletny dwudzielny graf K _{a , b} jest kografem. Jego cotree zakorzenione w 1-węzła, który ma dwa dzieci 0-węzła, jeden z a liści dzieci i jeden z b dzieci liści. Turan wykresu mogą być utworzone przez sprzężenie z rodziny równej wielkości niezależne zestawy; w związku z tym jest to również krzywa, z cotree zakorzenionym w 1-węźle, który ma podrzędny 0-węzeł dla każdego niezależnego zestawu.

Każdy wykres progowy jest również wykresem. Wykres progowy można utworzyć przez wielokrotne dodawanie jednego wierzchołka, połączonego ze wszystkimi poprzednimi wierzchołkami lub z żadnym z nich; każda taka operacja jest jedną z operacji rozłącznych lub połączonych, dzięki którym można utworzyć cotree.

Superklasy

Charakteryzacja kografów przez własność, że każda klika i maksymalny zbiór niezależny mają niepuste przecięcie, jest silniejszą wersją własności definiującej grafów silnie doskonałych , w której każdy podgraf indukowany zawiera zbiór niezależny, który przecina wszystkie kliki maksymalne. W kografie każdy maksymalny niezależny zbiór przecina wszystkie maksymalne kliki. Tak więc każdy wykres jest zdecydowanie doskonały.

Fakt, że wykresy są wolne od P ₄ oznacza, że ​​można je doskonale uporządkować . W rzeczywistości, każdy porządek wierzchołków w kografie jest porządkiem idealnym, co dalej implikuje, że maksymalne znajdowanie kliki i minimalne zabarwienie można znaleźć w czasie liniowym z dowolnym zachłannym kolorowaniem i bez potrzeby rozkładu cotree.

Każdy wykres jest wykresem dziedzicznym odległości , co oznacza, że ​​każda indukowana ścieżka w wykresie jest najkrótszą ścieżką . Kografy można scharakteryzować wśród wykresów dziedzicznych odległości jako mające średnicę dwa w każdym połączonym składniku. Każdy kograf również wykres porównywalność z szeregowo-równoległy porządek częściowy , otrzymuje się zastępując związek odłączony i operacji łączenia przez którą kograf był zbudowany przez rozłącznego jedności i porządkowe suma operacjach częściowych zamówień. Ponieważ wykresy silnie doskonałe, wykresy doskonale uporządkowane, wykresy dziedziczne na odległość i wykresy porównywalności są grafami doskonałymi , cographs również są doskonałe.

Uwagi

Bibliografia

Linki zewnętrzne

• „Wykresy z wykresami” , system informacyjny dotyczący włączeń klas na wykresach
• Weisstein, Eric W. "Kograf" . MatematykaŚwiat .