Bilard dynamiczny - Dynamical billiards

Cząstka poruszająca się na stadionie Bunimowicza, znany chaotyczny bilard. Zobacz sekcję Oprogramowanie, aby dowiedzieć się, jak wykonać taką animację.

Dynamiczne bilardowy jest układ dynamiczny , w którym A zmianę cząstek między wolnym tempie (na ogół w postaci linii prostej) i lustrzane odbicia od granicy. Kiedy cząstka uderza w granicę, odbija się od niej bez utraty prędkości (tj. zderzenia sprężyste). Bilard to hamiltonowskie idealizacje gry w bilard , ale obszar zawarty w granicy może mieć kształty inne niż prostokątne, a nawet być wielowymiarowe. Dynamiczny bilard można również badać na geometriach nieeuklidesowych ; rzeczywiście, pierwsze badania bilarda ustaliły ich ruch ergodyczny na powierzchniach o stałej ujemnej krzywiźnie . Badanie bilarda, który jest trzymany poza regionem, a nie jest trzymany w regionie, jest znane jako teoria bilarda zewnętrznego .

Ruch cząstki w bilardzie jest linią prostą o stałej energii pomiędzy odbiciami od granicy ( geodezja, jeśli metryka riemannowska stołu bilardowego nie jest płaska). Wszystkie odbicia są lustrzane : kąt padania tuż przed zderzeniem jest równy kątowi odbicia tuż po zderzeniu. Sekwencji odbić opisano przez mapę bilardowym który całkowicie charakteryzuje ruch cząstki.

Bilard ujmuje całą złożoność układów hamiltonowskich, od całkowalności do ruchu chaotycznego , bez trudności w całkowaniu równań ruchu w celu wyznaczenia jego odwzorowania Poincarégo . Birkhoff wykazał, że system bilardowy ze stołem eliptycznym jest całkowalny.

Równania ruchu

Hamiltona na cząstki o masie m poruszać się swobodnie bez tarcia na powierzchni jest:

${\ Displaystyle H (p, q) = {\ Frac {p ^ {2}} {2 m}} + V (q)}$

gdzie jest potencjałem zaprojektowanym jako zero wewnątrz obszaru, w którym cząsteczka może się poruszać, a nieskończoność w przeciwnym razie: ${\ Displaystyle V (q)}$${\ Displaystyle \ Omega}$

${\ Displaystyle V (q) = {\ zacząć {przypadki} 0 i q \ w \ Omega \ \ \ infty & q \ notin \ Omega \ koniec {przypadki}}}$

Taka forma potencjału gwarantuje lustrzane odbicie na granicy. Termin kinetyczny gwarantuje, że cząstka porusza się po linii prostej, bez zmiany energii. Jeżeli cząstka ma poruszać się po nieeuklidesowej rozmaitości , to hamiltonian otrzymujemy:

${\ Displaystyle H (p, q) = {\ Frac {1} {2 m}} p ^ {i} p ^ {j} g_ {ij} (q) + V (q)}$

gdzie jest tensor metryczny w punkcie . Ze względu na bardzo prostą strukturę tego hamiltonianu, równania ruchu dla cząstki, równania Hamiltona-Jacobiego , są niczym innym jak równaniami geodezyjnymi na rozmaitości: cząstka porusza się wzdłuż geodezji . ${\ Displaystyle g_ {ij} (q)}$${\displaystyle q\;\w \;\omega}$

Wybitne bilardy i klasy bilardowe

Bilard Hadamarda

Bilard Hadamarda dotyczy ruchu punktu swobodnego po powierzchni o stałej ujemnej krzywiźnie, w szczególności najprostszej zwartej powierzchni Riemanna o ujemnej krzywiźnie, powierzchni z rodzaju 2 (pączek z dwoma otworami). Model jest dokładnie rozwiązywalny i wynika z przepływu geodezyjnego na powierzchni. Jest to najwcześniejszy przykład deterministycznego chaosu, jaki kiedykolwiek badano, wprowadzony przez Jacquesa Hadamarda w 1898 roku.

Bilard Artina

Bilard Artina rozważa swobodny ruch cząstki punktowej na powierzchni o stałej ujemnej krzywiźnie, w szczególności najprostszą niezwartą powierzchnię Riemanna , powierzchnię z jednym wierzchołkiem. Wyróżnia się tym, że jest dokładnie rozwiązywalny, a jednocześnie nie tylko ergodyczny, ale także silnie mieszający . Jest to przykład systemu Anosov . Ten system został po raz pierwszy zbadany przez Emila Artina w 1924 roku.

Bilard dyspersyjny i półdyspersyjny

Niech M będzie zupełną gładką rozmaitością Riemanna bez granicy, której maksymalna krzywizna przekroju jest nie większa niż K io promieniu injektywności . Rozważmy zbiór n geodezyjnie wypukłych podzbiorów (ścian) , , tak aby ich granice były gładkimi podrozmaitościami miareczkowej 1. Niech , gdzie oznacza wnętrze zestawu . Zestaw będzie się nazywał stołem bilardowym. Rozważmy teraz cząstkę, która porusza się wewnątrz zbioru B z jednostkową prędkością wzdłuż geodezji, aż dotrze do jednego ze zbiorów B _i (takie zdarzenie nazywa się zderzeniem), gdzie odbija zgodnie z prawem „kąt padania jest równy kąt odbicia” (jeśli osiągnie jeden ze zbiorów , , po tym momencie trajektoria nie jest określona). Taki układ dynamiczny nazywamy bilardem półdyspersyjnym . Jeśli ściany są ściśle wypukłe, to bilard nazywa się rozpraszaniem . Nazewnictwo motywowane jest obserwacją, że lokalnie równoległa wiązka trajektorii rozprasza się po zderzeniu ze ściśle wypukłą częścią ściany, ale pozostaje lokalnie równoległa po zderzeniu z płaskim odcinkiem ściany. ${\ Displaystyle \ rho > 0}$${\ Displaystyle B_ {i} \ podzbiór M}$${\displaystyle i=1,\ldots,n}$${\ Displaystyle B = M \ (\ bigcup _ {i = 1} ^ {n} \ operatorname {int} (B_ {i}))}$${\ Displaystyle \ Operatorname {Int} (B_ {i})}$${\displaystyle B_{i}}$${\displaystyle B\podzbiór M}$${\ Displaystyle B_ {i} \ czapka B_ {j}}$${\displaystyle i\neqj}$

Granica dyspersyjna odgrywa taką samą rolę dla bilarda, jak ujemna krzywizna dla przepływów geodezyjnych, powodując wykładniczą niestabilność dynamiki. To właśnie ten mechanizm dyspergowania nadaje bilardowi dyspersyjnemu najsilniejsze właściwości chaotyczne , jak to ustalił Jakow G. Synaj . Mianowicie, bilard są ergodyczny , mieszanie , Bernoulli , mający pozytywny Kołmogorowa-Sinai entropii oraz rozkład wykładniczy o korelacji .

Chaotyczne właściwości ogólnych bilardów semidyspersyjnych nie są tak dobrze rozumiane, jednak właściwości jednego ważnego typu bilarda semidyspersyjnego, gazu twardej kuli, były szczegółowo badane od 1975 roku (patrz następny rozdział).

Ogólne wyniki Dmitri Burago i Serge Ferleger dotyczące równomiernego oszacowania liczby zderzeń w niezdegenerowanym półdyspersyjnym bilardzie pozwalają ustalić skończoność jego entropii topologicznej i nie więcej niż wykładniczy wzrost trajektorii okresowych. W przeciwieństwie do tego, zdegenerowany bilard z półdyspersją może mieć nieskończoną entropię topologiczną.

Gaz Lorentza, czyli bilard Synaj

Cząstka poruszająca się w bilardzie Synaj, znana również jako gaz Lorentza.

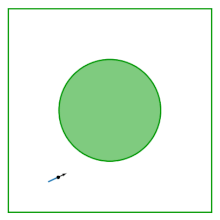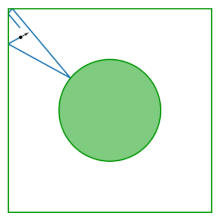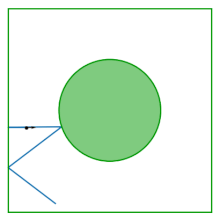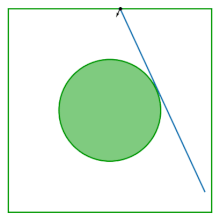
Stół gazu Lorentza (znany również jako bilard Synaj) to kwadrat z dyskiem usuniętym ze środka; stół jest płaski, bez krzywizny. Bilard powstaje w wyniku badania zachowania dwóch oddziałujących ze sobą dysków odbijających się wewnątrz kwadratu, odbijających się od granic kwadratu i od siebie nawzajem. Eliminując środek masy jako zmienną konfiguracyjną, dynamika dwóch współpracujących ze sobą dysków redukuje się do dynamiki w bilardzie Synaj.

Bilard został przedstawiony przez Jakow G. Sinai jako przykład oddziałującego układu hamiltonowskiego, który wykazuje fizyczne właściwości termodynamiczne: prawie wszystkie (aż do zera) jego możliwe trajektorie są ergodyczne i ma dodatni wykładnik Lapunowa .

Wielkim osiągnięciem Synaju z tym modelem było wykazanie, że klasyczny zespół Boltzmanna-Gibbsa dla gazu doskonałego jest w istocie maksymalnie chaotycznym bilardem Hadamarda.

Stadion Bunimowicza

Stół zwany stadionem Bunimowicza to prostokąt zamknięty półokręgami, kształt zwany stadionem . Do czasu wprowadzenia go przez Leonida Bunimowicza uważano , że bilard z dodatnimi wykładnikami Lapunowa wymaga wypukłych rozpraszaczy, takich jak dysk w bilardzie Synaj, aby wytworzyć wykładniczą dywergencję orbit. Bunimovich wykazał, że rozpatrując orbity poza punktem ogniskowania obszaru wklęsłego, można było uzyskać dywergencję wykładniczą.

Bilard magnetyczny

Ruch naładowanej cząstki w bilardzie Synaj z prostopadłym polem magnetycznym.

Bilard magnetyczny reprezentuje bilard, w którym naładowana cząstka rozchodzi się w obecności prostopadłego pola magnetycznego. W rezultacie trajektoria cząstki zmienia się z linii prostej w łuk koła. Promień tego okręgu jest odwrotnie proporcjonalny do natężenia pola magnetycznego. Takie bilardy były przydatne w rzeczywistych zastosowaniach bilarda, zazwyczaj w modelowaniu nanourządzeń (patrz Aplikacje).

Bilard uogólniony

Bilard uogólniony (GB) opisuje ruch punktu masy (cząstki) wewnątrz zamkniętej domeny z gładką odcinkowo granicą . Na granicy prędkość punktu jest przekształcana, gdy cząstka podlega działaniu uogólnionego prawa bilardowego. GB zostały wprowadzone przez Lwa D. Pustyl'nikowa w ogólnym przypadku, aw przypadku gdy jest równoległościanem w związku z uzasadnieniem drugiej zasady termodynamiki . Z fizycznego punktu widzenia GB opisują gaz składający się ze skończonych wielu cząstek poruszających się w naczyniu, podczas gdy ściany naczynia nagrzewają się lub ochładzają. Istota uogólnienia jest następująca. Gdy cząstka uderza w granicę , jej prędkość zmienia się za pomocą danej funkcji , określonej na iloczynie bezpośrednim (gdzie jest linia rzeczywista, jest punktem granicy, a jest czasem), zgodnie z następującym prawem. Załóżmy, że trajektoria cząstki, która porusza się z prędkością , przecina się w momencie . Z czasem cząstka nabiera prędkości , jakby przeszła sprężyste pchnięcie od płaszczyzny nieskończenie ciężkiej , która jest styczna do w punkcie , a czasem porusza się wzdłuż normalnej do w z prędkością . Podkreślamy, że położenie samej granicy jest ustalone, a jej działanie na cząstkę jest określone funkcją . ${\ Displaystyle \ Pi \ \ podzbiór \ \ mathbb {R} ^ {n}}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ Pi}$${\ Displaystyle \ Gamma}$${\displaystyle f(\gamma,\,t)}$${\ Displaystyle \ Gamma \ \ razy \ \ mathbb {R} ^ {1}}$${\ Displaystyle \ mathbb {R} ^ {1}}$${\ Displaystyle \ gamma \ \ w \ \ Gamma}$${\ Displaystyle t \ \ w \ \ mathbb {R} ^ {1}}$${\displaystyle v}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ gamma \ \ w \ \ Gamma}$${\ Displaystyle t ^ {*}}$${\ Displaystyle t ^ {*}}$${\ Displaystyle v ^ {*}}$${\ Displaystyle \ Gamma ^ {*}}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ gamma}$${\ Displaystyle t ^ {*}}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ gamma}$${\ Displaystyle \ textstyle {\ Frac {\ częściowy f} {\ częściowy t}} (\ gamma, \, t ^ {*})}$${\displaystyle f}$

Bierzemy pozytywny kierunek ruchu samolotu się w kierunku wnętrza od . Zatem jeśli pochodna , to po zderzeniu cząstka przyspiesza. ${\ Displaystyle \ Gamma ^ {*}}$${\ Displaystyle \ Pi}$${\displaystyle \textstyle {\frac {\częściowy f}{\częściowy t}}(\gamma,\,t)\;>\;0}$

Jeżeli prędkość , uzyskana przez cząstkę w wyniku powyższego prawa odbicia, zostanie skierowana do wnętrza domeny , wówczas cząstka opuści granicę i będzie się poruszała aż do następnego zderzenia z . Jeśli prędkość jest skierowana na zewnątrz , wtedy cząstka pozostaje w tym punkcie, aż w pewnym momencie oddziaływanie z granicą zmusi cząstkę do jej opuszczenia. ${\ Displaystyle v ^ {*}}$${\ Displaystyle \ Pi}$${\ Displaystyle \ Pi}$${\ Displaystyle \ Gamma}$${\ Displaystyle v ^ {*}}$${\ Displaystyle \ Pi}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ gamma}$${\displaystyle {\tylda {t}}\;>\;t^ {*}}$

Jeśli funkcja nie zależy od czasu ; tj . uogólniony bilard pokrywa się z klasycznym. ${\displaystyle f(\gamma,\,t)}$${\displaystyle t}$${\displaystyle \textstyle {\frac {\częściowy f}{\częściowy t}}\;=\;0}$

To uogólnione prawo refleksji jest bardzo naturalne. Po pierwsze, odzwierciedla oczywisty fakt, że ściany naczynia z gazem są nieruchome. Po drugie, działanie ściany na cząstkę jest nadal klasycznym sprężystym pchnięciem. W istocie rozważamy poruszające się w nieskończoność granice z określonymi prędkościami.

Jest uważany za odbicie od granicy zarówno w ramach mechaniki klasycznej (przypadek Newtona), jak i teorii względności (przypadek relatywistyczny). ${\ Displaystyle \ Gamma}$

Główne wyniki: w przypadku newtonowskim energia cząstki jest ograniczona, entropia Gibbsa jest stałą (w przypisach), a w przypadku relatywistycznym energia cząstki, entropia Gibbsa, entropia względem objętości fazy rośnie do nieskończoności, (w uwagach), odniesienia do uogólnionego bilarda.

Chaos kwantowy

Kwantowa wersja bilarda jest łatwo badana na kilka sposobów. Podany powyżej klasyczny hamiltonian dla bilarda zostaje zastąpiony równaniem Schrödingera w stanie stacjonarnym , a dokładniej: ${\ Displaystyle H \ psi \; = \; E \ psi}$

${\ Displaystyle - {\ Frac {\ hbar ^ {2}} {2 m}} \ nabla ^ {2} \ psi _ {n} (q) = E_ {n} \ psi _ {n} (q)}$

gdzie jest Laplacek . Potencjał, który jest nieskończony poza regionem, ale zero w nim, przekłada się na warunki brzegowe Dirichleta : ${\ Displaystyle \ nabla ^ {2}}$${\ Displaystyle \ Omega}$

${\ Displaystyle \ psi _ {n} (q) = 0 \ quad {\ mbox {dla}} \ quad q \ notin \ Omega}$

Jak zwykle przyjmuje się, że funkcje falowe są ortonormalne :

${\ Displaystyle \ int _ {\ Omega} {\ overline {\ psi _ {m}}} (q) \ psi _ {n} (q) \, dq = \ delta _ {mn}}$

Co ciekawe, równanie Schrödingera w polu swobodnym jest takie samo jak równanie Helmholtza ,

${\ Displaystyle \ lewo (\ nabla ^ {2} + k ^ {2} \ prawo) \ psi = 0}$

z

${\ Displaystyle k ^ {2} = {\ Frac {1} {\ hbar ^ {2}}} 2mE_ {n}}$

Oznacza to, że dwu- i trójwymiarowy bilard kwantowy można modelować klasycznymi modami rezonansowymi wnęki radarowej o określonym kształcie, co otwiera drogę do eksperymentalnej weryfikacji. (Badanie modów wnęki radaru musi być ograniczone do poprzecznych modów magnetycznych (TM), ponieważ są one zgodne z warunkami brzegowymi Dirichleta).

Półklasyczna granica odpowiada której można uznać za równoważną , masa wzrasta tak, że zachowuje się klasycznie. ${\ Displaystyle \ hbar \; \ do \; 0}$${\displaystyle m\;\do \;\infty}$

Ogólnie można powiedzieć, że ilekroć klasyczne równania ruchu są całkowalne (np. prostokątne lub okrągłe stoły bilardowe), to kwantowo-mechaniczna wersja bilarda jest całkowicie rozwiązywalna. Kiedy system klasyczny jest chaotyczny, to system kwantowy jest generalnie nie do końca rozwiązywalny i stwarza liczne trudności w jego kwantyzacji i ocenie. Ogólne badanie chaotycznych systemów kwantowych jest znane jako chaos kwantowy .

Szczególnie uderzający przykład blizn na stole eliptycznym daje obserwacja tak zwanego mirażu kwantowego .

Aplikacje

Bilard, zarówno kwantowy, jak i klasyczny, został zastosowany w kilku dziedzinach fizyki do modelowania całkiem zróżnicowanych systemów świata rzeczywistego. Przykłady obejmują optykę promieniową , lasery , akustykę , światłowody (np. włókna podwójnie płaszczowe ) lub korespondencję klasyczną kwantową. Jednym z ich najczęstszych zastosowań jest modelowanie cząstek poruszających się wewnątrz nanourządzeń, np. kropek kwantowych , połączeń pn , supersieci antidotowych . Powodem tej szeroko rozpowszechnionej skuteczności bilarda jako modeli fizycznych jest fakt, że w sytuacjach z niewielką ilością nieporządku lub szumu ruch np. cząstek, takich jak elektrony czy promienie świetlne, jest bardzo podobny do ruchu punktu. cząstki w bilard. Ponadto, charakter zderzeń cząstek z zachowaniem energii jest bezpośrednim odzwierciedleniem zachowania energii w mechanice hamiltonowskiej.

Oprogramowanie

Oprogramowanie open source do symulacji bilarda istnieje dla różnych języków programowania. Od najnowszego do najstarszego, istniejące oprogramowanie to: DynamicalBilliards.jl (Julia), Bill2D (C++) i Billiard Simulator (Matlab). Animacje prezentowane na tej stronie zostały wykonane za pomocą DynamicalBilliards.jl.

Zobacz też

• Model Fermi-Ulam (bilard z oscylacyjnymi ścianami)
• Algorytm kompresji Lubaczewskiego-Stillingera symuluje twarde kule zderzające się nie tylko z granicami, ale także między sobą podczas wzrostu rozmiarów
• Bilard arytmetyczny

Uwagi

Bibliografia

Bilard Synaj

• Synaj, Ja. G. (1963). „[Na podstawach hipotezy ergodycznej dla dynamicznego układu mechaniki statystycznej]”. Doklady Akademii Nauk SSSR (po rosyjsku). 153 (6): 1261–1264.(w języku angielskim, Sov. Math Dokl. 4 (1963) s. 1818–1822).
• Tak. G. Sinai, "Systemy dynamiczne z odbiciami elastycznymi", Russian Mathematical Surveys , 25 , (1970) s. 137-191.
• VI Arnold i A. Avez, Théorie ergodique des systèms dynamiques , (1967), Gauthier-Villars, Paryż. (Wydanie angielskie: Benjamin-Cummings, Reading, Mass. 1968). (Zawiera dyskusję i odniesienia do bilarda Synaju.)
• D. Heitmann, JP Kotthaus, "Spektroskopia macierzy kropek kwantowych", Physics Today (1993) s. 56-63. (Zawiera przegląd eksperymentalnych testów wersji kwantowych bilarda Synaju zrealizowanych jako struktury w nanoskali (mezoskopowe) na płytkach krzemowych.)
• S. Sridhar i WT Lu, „ Sinai Billiards, Ruelle Zeta-functions and Ruelle Resonances: Microwave Experiments ”, (2002) Journal of Statistical Physics , tom. 108 nr 5/6, s. 755–766.
• Linas Vepstas, Bilard Synaju , (2001). (Zapewnia trójwymiarowe obrazy bilarda Synaju za pomocą śledzenia promieni. Obrazy te zapewniają graficzną, intuicyjną demonstrację silnej ergodyczności systemu.)
• N. Chernov i R. Markarian, „Chaotic Billiards”, 2006, Ankieta matematyczna i monografie nr 127, AMS.

Dziwny bilard

• T. Schürmann i I. Hoffmann, Entropia dziwnych bilardów w n-simpleksach. J. Fiz. A28, strona 5033ff, 1995. Dokument PDF

Stadion Bunimowicza

• LABunimowicz (1979). „Na właściwościach ergodycznych nigdzie rozpraszanie bilard”. Wspólna Matematyka Fizyka . 65 (3): 295-312. Kod Bib : 1979CMaPh..65..295B . doi : 10.1007/BF01197884 .
• LABunimovich i Ja. G. Synaj (1980). „Przegrody Markowa dla rozproszonego bilardu”. Wspólna Matematyka Fizyka . 78 (2): 247–280. Kod Bibcode : 1980CMaPh..78..247B . doi : 10.1007/bf01942372 .
• Animacja flash ilustrująca chaotyczny stadion Bunimowicza

Bilard uogólniony

• MV Deryabin i LD Pustyl'nikov, „Uogólniony bilard relatywistyczny”, Reg. i Chaotyczny Dyn. 8(3), s. 283–296 (2003).
• MV Deryabin i LD Pustyl'nikov, "O uogólnionym relatywistycznym bilardzie w zewnętrznych polach sił", Letters in Mathematical Physics , 63(3), s. 195-207 (2003).
• MV Deryabin i LD Pustyl'nikov, "Wykładnicze atraktory w uogólnionym relatywistycznym bilardzie", Comm. Matematyka. Fiz. 248(3), s. 527-552 (2004).

Linki zewnętrzne

• Weisstein, Eric W. „Bilard” . MatematykaŚwiat .
• Wpis Scholarpedia na temat dynamicznego bilarda (Leonid Bunimovich)
• Wprowadzenie do układów dynamicznych z wykorzystaniem bilarda , Max Planck Institute for the Physics of Complex Systems