Mnożnik Lagrange'a - Lagrange multiplier

W optymalizacji matematycznej The metoda mnożników Lagrange'a to strategia na znalezienie lokalnego minimum i maksimum o funkcji zastrzeżeniem ograniczeń równości (czyli pod warunkiem, że jeden lub więcej równania muszą być spełnione dokładnie przez wybranych wartościach zmiennych ). Jego nazwa pochodzi od matematyka Josepha-Louisa Lagrange'a . Podstawową ideą jest przekształcenie problemu z ograniczeniami do postaci takiej, aby test różniczkowy problemu nieograniczonego nadal mógł być zastosowany. Związek między gradientem funkcji a gradientami więzów raczej naturalnie prowadzi do przeformułowania pierwotnego problemu, znanego jako funkcja Lagrange'a .

Metodę można podsumować w następujący sposób: aby znaleźć maksimum lub minimum funkcji podlegającej ograniczeniu równości , utwórz funkcję Lagrange'a ${\displaystyle f(x)}$${\ Displaystyle g (x) = 0}$

${\ Displaystyle {\ mathcal {L}} (x \ lambda) = f (x) - \ lambda g (x)}$

i znaleźć punkty stacjonarne z uważany jako funkcja i mnożnika Lagrange'a . Rozwiązanie odpowiadające pierwotnego ograniczonym optymalizacji jest zawsze punkt siodłowy z Lagrange'a funkcji, która może być zidentyfikowana pomiędzy stacjonarnymi punktami z konkretności w graniczącym Heskiego matrycy . ${\displaystyle {\mathcal {L}}}$${\displaystyle x}$${\ Displaystyle \ lambda}$

Wielką zaletą tej metody jest to, że umożliwia ona rozwiązanie optymalizacji bez jawnej parametryzacji pod kątem ograniczeń. W rezultacie metoda mnożników Lagrange'a jest szeroko stosowana do rozwiązywania trudnych problemów związanych z ograniczoną optymalizacją. Co więcej, metoda mnożników Lagrange'a jest uogólniona przez warunki Karusha-Kuhna-Tuckera , które mogą również uwzględniać ograniczenia nierównościowe postaci . ${\displaystyle h(\mathbf {x} )\leq c}$

Oświadczenie

Poniższe jest znane jako twierdzenie o mnożniku Lagrange'a.

Niech będzie funkcją celu, będzie funkcją ograniczeń, obie należące do (tj. mające ciągłe pierwsze pochodne). Niech będzie optymalnym rozwiązaniem następującego problemu optymalizacyjnego, takim, że ranga : ${\ Displaystyle f \ dwukropek \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R}}$${\ Displaystyle g \ dwukropek \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {c}}$${\ Displaystyle C ^ {1}}$${\ Displaystyle x ^ {*}}$${\ Displaystyle Dg (x ^ {*}) = c < n}$

${\ Displaystyle {\ tekst {maksymalizacja}} \ f (x)}$

${\ Displaystyle {\ tekst {z zastrzeżeniem:}} \ g (x) = 0}$

(Tutaj oznacza macierz pochodnych cząstkowych, .) ${\ Displaystyle Dg (x ^ {*})}$${\ Displaystyle \ lewo [{\ Frac {\ częściowy g_ {j}} {\ częściowy x_ {k}}} \ po prawej]}$

Istnieją też unikalne mnożniki Lagrange'a takie, że . ${\ Displaystyle \ lambda ^ {*} \ w \ mathbb {R} ^ {c}}$${\ Displaystyle Df (x ^ {*}) = \ lambda ^ {* T} Dg (x ^ {*})}$

Twierdzenie Lagrange'a o mnożniku mówi, że w dowolnym lokalnym maksimach (lub minimach) funkcji ocenianej w warunkach równości, jeśli kwalifikacja ograniczenia ma zastosowanie (wyjaśniono poniżej), wówczas gradient funkcji (w tym punkcie) można wyrazić jako kombinację liniową gradientów ograniczeń (w tym punkcie), przy czym mnożniki Lagrange'a pełnią rolę współczynników . Jest to równoznaczne z stwierdzeniem, że każdy kierunek prostopadły do ​​wszystkich gradientów więzów jest również prostopadły do ​​gradientu funkcji. Albo jeszcze mówiąc, że pochodna kierunkowa funkcji wynosi 0 w każdym możliwym kierunku.

Pojedyncze ograniczenie

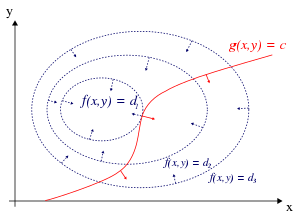
W przypadku tylko jednego ograniczenia i tylko dwóch zmiennych wyboru (jak pokazano na rysunku 1), rozważ problem optymalizacji

${\ Displaystyle {\ tekst {maksymalizacja}} \ f (x, y)}$

${\ Displaystyle {\ tekst {z zastrzeżeniem:}} \ g (x, y) = 0}$

(Czasami stała addytywna jest pokazywana osobno, a nie jest zawarta w , w którym to przypadku więz jest napisany , jak na rysunku 1.) Zakładamy, że obie i mają ciągłe pierwsze pochodne cząstkowe . Wprowadzamy nową zmienną ( ) zwaną mnożnikiem Lagrange'a (lub nieokreślony mnożnik Lagrange'a ) i badamy funkcję Lagrange'a (lub wyrażenie Lagrange'a lub Lagrange'a ) zdefiniowaną przez ${\displaystyle g}$${\ Displaystyle g (x, y) = c}$${\displaystyle f}$${\displaystyle g}$${\ Displaystyle \ lambda}$

${\ Displaystyle {\ mathcal {L}} (x, y, \ lambda ) = f (x, y) - \ lambda g (x, y)}$

gdzie termin może być dodany lub odjęty. Jeżeli jest maksimum dla pierwotnego problemu z ograniczeniami i , to istnieje takie, że ( ) jest punktem stacjonarnym dla funkcji Lagrange'a (punkty stacjonarne to te punkty, w których pierwsze pochodne cząstkowe są równe zeru). Założenie to nazywa się kwalifikacją ograniczenia. Jednak nie wszystkie punkty stacjonarne dają rozwiązanie pierwotnego problemu, ponieważ metoda mnożników Lagrange'a daje tylko warunek konieczny optymalności w problemach z ograniczeniami. Istnieją również warunki dostateczne dla minimum lub maksimum , ale jeśli dane rozwiązanie kandydata spełnia warunki wystarczające, to gwarantuje się tylko, że rozwiązanie to jest najlepsze lokalnie – czyli lepsze niż jakiekolwiek dopuszczalne pobliskie punkty. Globalny optymalne można znaleźć przez porównywanie wartości pierwotnej funkcji celu w punktach spełniających konieczne i wystarczające lokalne warunki. ${\ Displaystyle \ lambda}$${\displaystyle f(x_{0},y_{0})}$${\displaystyle f(x,y)}$${\ Displaystyle \ nabla g (x_ {0}, Y_ {0}) \ neq 0}$${\ Displaystyle \ lambda _ {0}}$${\displaystyle x_{0},y_{0},\lambda_{0}}$${\displaystyle {\mathcal {L}}}$${\ Displaystyle \ nabla g \ neq 0}$

Metoda mnożników Lagrange'a opiera się na intuicji, że w maksimum f ( x , y ) nie może rosnąć w kierunku takiego sąsiedniego punktu, który również ma g = 0 . Gdyby tak było, moglibyśmy iść wzdłuż g = 0, aby dostać się wyżej, co oznacza, że ​​punkt początkowy nie jest w rzeczywistości maksimum. Patrząc w ten sposób, jest to dokładny analog do testowania, czy pochodna funkcji nieograniczonej wynosi 0, to znaczy sprawdzamy, czy pochodna kierunkowa wynosi 0 w dowolnym istotnym (realnym) kierunku.

Można wyobrazić kontury o f podane przez F ( x , y ) = d dla różnych wartości d i kontur g podaje g ( x , y ) = C .

Załóżmy, że idziemy wzdłuż linii konturowej z g = c . Interesuje nas znalezienie punktów, w których f prawie się nie zmienia podczas spaceru, ponieważ te punkty mogą być maksimami.

Mogą się to zdarzyć na dwa sposoby:

1. Moglibyśmy dotknąć konturu f , ponieważ z definicji f nie zmienia się, gdy idziemy wzdłuż jego konturów. Oznaczałoby to, że styczne do warstwic f i g są tutaj równoległe.
2. Osiągnęliśmy „poziomową” część f , co oznacza, że f nie zmienia się w żadnym kierunku.

Aby sprawdzić pierwszą możliwość (dotykamy warstwic f ), zauważ, że ponieważ gradient funkcji jest prostopadły do ​​warstwic, styczne do warstwic f i g są równoległe wtedy i tylko wtedy, gdy gradienty f i g są równoległe. Zatem chcemy punktów ( x , y ) gdzie g ( x , y ) = c i

${\ Displaystyle \ nabla _ {x, y} f = \ lambda \, \ nabla _ {x, y} g}$

dla niektórych ${\ Displaystyle \ lambda}$

gdzie

${\ Displaystyle \ nabla _ {x, y} f = \ lewo ({\ Frac {\ częściowy f} {\ częściowy x}}, {\ Frac {\ częściowy f} {\ częściowy Y}} \ prawej), \ qquad \nabla _{x,y}g=\left({\frac {\częściowy g}{\częściowy x}},{\frac {\częściowy g}{\częściowy y}}\right)}$

są odpowiednie gradienty. Stała jest wymagana, ponieważ chociaż dwa wektory gradientu są równoległe, wielkości wektorów gradientu na ogół nie są równe. Ta stała nazywana jest mnożnikiem Lagrange'a. (W niektórych konwencjach poprzedza znak minus). ${\ Displaystyle \ lambda}$${\ Displaystyle \ lambda}$

Zauważ, że ta metoda rozwiązuje również drugą możliwość, że f jest poziomem: jeśli f jest poziomem, to jego gradient wynosi zero, a ustawienie jest rozwiązaniem niezależnie od . ${\ Displaystyle \ lambda = 0}$${\ Displaystyle \ nabla _ {x, y} g}$

Aby włączyć te warunki do jednego równania, wprowadzamy funkcję pomocniczą

${\ Displaystyle {\ mathcal {L}} (x, y, \ lambda ) = f (x, y) - \ lambda g (x, y)}$

i rozwiąż

${\ Displaystyle \ nabla _ {x, y \ lambda} {\ mathcal {L}} (x, y \ lambda) = 0.}$

Zauważ, że równa się to rozwiązaniu trzech równań w trzech niewiadomych. To jest metoda mnożników Lagrange'a.

Zauważ , że implikuje , jako pochodna cząstkowa względem is , które wyraźnie wynosi zero wtedy i tylko wtedy, gdy . ${\ Displaystyle \ nabla _ {\ lambda} {\ mathcal {L}} (x, y \ lambda) = 0}$${\ Displaystyle g (x, y) = 0}$${\displaystyle {\mathcal {L}}}$${\ Displaystyle \ lambda}$${\displaystyle -g(x,y)}$${\ Displaystyle g (x, y) = 0}$

Podsumowując

${\ Displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0 \ iff {\ zacząć {przypadki} \ nabla _ {x, y} f (x ,y)=\lambda \,\nabla _{x,y}g(x,y)\\g(x,y)=0\end{przypadki}}}$

Metoda łatwo uogólnia funkcje na zmienne ${\ Displaystyle n}$

${\ Displaystyle \ nabla _ {x_ {1}, \ kropki, x_ {n}, \ lambda} {\ mathcal {l}} (x_ {1}, \ kropki, x_ {n}, \ lambda) = 0}$

co sprowadza się do rozwiązania n + 1 równań w n + 1 niewiadomych.

Ograniczonego ekstrema f są krytyczne punkty z Lagrange'a , ale nie koniecznie są lokalne ekstrema z (patrz przykład 2 poniżej). ${\displaystyle {\mathcal {L}}}$${\displaystyle {\mathcal {L}}}$

Można przeformułować lagranżian na hamiltonian , w którym to przypadku rozwiązania są lokalnymi minimami dla hamiltonianu. Odbywa się to w teorii kontroli optymalnej , w formie zasady minimum Pontryagina .

Fakt, że rozwiązania Lagrange'a niekoniecznie są ekstremami, również nastręcza trudności w optymalizacji numerycznej. Można to rozwiązać, obliczając wielkość gradientu, ponieważ zera wielkości są z konieczności lokalnymi minimami, jak zilustrowano w przykładzie optymalizacji numerycznej .

Wiele ograniczeń

Metodę mnożników Lagrange'a można rozszerzyć do rozwiązywania problemów z wieloma ograniczeniami przy użyciu podobnego argumentu. Rozważmy paraboloidę podlegającą ograniczeniom liniowym, które przecinają się w jednym punkcie. Jako jedyne możliwe rozwiązanie, ten punkt jest oczywiście ograniczonym ekstremum. Jednakże zestaw poziom z wyraźnie nie równolegle do obu ograniczeń, w punkcie przecięcia (patrz figura 3); zamiast tego jest to liniowa kombinacja gradientów dwóch ograniczeń. W przypadku więzów wielokrotnych tego właśnie szukamy: metoda Lagrange'a poszukuje punktów, w których gradient nie jest koniecznie wielokrotnością gradientu pojedynczego ograniczenia, ale w którym jest to liniowa kombinacja wszystkich więzów”. gradienty. ${\displaystyle f}$${\displaystyle f}$

Konkretnie załóżmy, że mamy ograniczenia i poruszamy się po zbiorze punktów spełniających wymagania . Każdy punkt na konturze danej funkcji więzów ma przestrzeń dopuszczalnych kierunków: przestrzeń wektorów prostopadłych do . Zbiór kierunków dozwolonych przez wszystkie więzy jest zatem przestrzenią kierunków prostopadłych do wszystkich gradientów więzów. Oznacz tę przestrzeń dopuszczalnych ruchów przez i oznacz rozpiętość gradientów wiązań przez . Wtedy przestrzeń wektorów prostopadłych do każdego elementu . ${\ Displaystyle M}$${\ Displaystyle g_ {i} (\ mathbf {x}) = 0, i = 1, \ kropki, M}$${\displaystyle \mathbf {x}}$${\displaystyle g_{i}}$${\ Displaystyle \ nabla g_ {i} (\ mathbf {x})}$${\ Displaystyle A}$${\displaystyle S}$${\ Displaystyle A = S ^ {\ sprawca}}$${\displaystyle S}$

Nadal jesteśmy zainteresowani znajdowaniem punktów, w których nie zmienia się podczas spaceru, ponieważ te punkty mogą być (ograniczone) ekstremami. Dlatego szukamy takiego, aby każdy dopuszczalny kierunek ruchu od był prostopadły do (w przeciwnym razie moglibyśmy zwiększyć , poruszając się wzdłuż tego dopuszczalnego kierunku). Innymi słowy, . Tak więc istnieją skalary takie, że ${\displaystyle f}$${\displaystyle \mathbf {x}}$${\displaystyle \mathbf {x}}$${\ Displaystyle \ nabla f (\ mathbf {x} )}$${\displaystyle f}$${\ Displaystyle \ nabla f (\ mathbf {x}) \ w A ^ {\ sprawca} = S}$${\ Displaystyle \ lambda _ {1} \ lambda _ {2}, .... \ lambda _ {M}}$

${\ Displaystyle \ nabla f (\ mathbf {x} ) = \ suma _ {k = 1} ^ {M} \ lambda _ {k} \ \ nabla g_ {k} (\ mathbf {x}) \ quad \ iff \quad \nabla f(\mathbf {x} )-\sum _{k=1}^{M}{\lambda _{k}\nabla g_{k}(\mathbf {x} )}=0. }$

Te skalary są mnożnikami Lagrange'a. Mamy ich teraz , po jednym na każde ograniczenie. ${\ Displaystyle M}$

Tak jak poprzednio wprowadzamy funkcję pomocniczą

${\ Displaystyle {\ mathcal {L}} \ lewo (x_ {1}, \ ldots, x_ {n}, \ lambda _ {1}, \ ldots, \ lambda _ {M} \ po prawej) = f \ po lewej ( x_{1},\ldots ,x_{n}\right)-\sum \limits _{k=1}^{M}{\lambda _{k}g_{k}\left(x_{1},\ ldots ,x_{n}\prawo)}}$

i rozwiąż

${\ Displaystyle \ nabla _ {x_ {1}, \ ldots, x_ {n}, \ lambda _ {1}, \ ldots, \ lambda _ {M}} {\ mathcal {L}} (x_ {1}, \ldots ,x_{n},\lambda _{1},\ldots ,\lambda _{M})=0\iff {\begin{przypadki}\nabla f(\mathbf {x} )-\sum _{ k=1}^{M}{\lambda _{k}\,\nabla g_{k}(\mathbf {x} )}=0\\g_{1}(\mathbf {x} )=\cdots = g_{M}(\mathbf {x} )=0\end{przypadki}}}$

co sprowadza się do rozwiązywania równań w niewiadomych. ${\displaystyle n+M}$${\displaystyle n+M}$

Założeniem kwalifikacji ograniczeń, gdy istnieje wiele ograniczeń, jest to, że gradienty ograniczeń w odpowiednim punkcie są liniowo niezależne.

Nowoczesne formułowanie przez rozmaitości różniczkowe

Problem znajdowania lokalnych maksimów i minimów podlegających ograniczeniom można uogólnić na znalezienie lokalnych maksimów i minimów na rozmaitości różniczkowej . W dalszej części nie jest konieczne, aby była to przestrzeń euklidesowa ani nawet rozmaitość riemannowska. Wszystkie wyglądy gradientu (zależne od wyboru metryki riemannowskiej) można zastąpić zewnętrzną pochodną . ${\ Displaystyle M}$${\ Displaystyle M}$${\displaystyle \nabla}$ ${\displaystyle d}$

Pojedyncze ograniczenie

Niech będzie gładką rozmaitością wymiaru . Załóżmy, że chcemy znaleźć punkty stacjonarne funkcji gładkiej ograniczonej do podrozmaitości zdefiniowanej przez gdzie jest funkcją gładką, dla której 0 jest wartością regularną . ${\ Displaystyle M}$${\ Displaystyle m}$${\displaystyle x}$${\ Displaystyle f: M \ do \ mathbb {R} }$${\ Displaystyle N}$${\ Displaystyle g (x) = 0,}$${\ Displaystyle g: M \ do \ mathbb {R} }$

Niech i bądź zewnętrznymi pochodnymi . Stacjonarność dla ograniczenia przy średnich Równoważnie, jądro zawiera Innymi słowy, i są proporcjonalnymi 1-formami. W tym celu konieczne i wystarczające jest, aby następujący układ równań był spełniony: ${\displaystyle df}$${\displaystyle dg}$${\ Displaystyle f | _ {N}}$${\displaystyle x\w n}$${\ Displaystyle d (f | _ {N}) _ {x} = 0.}$${\ Displaystyle \ ker (df_ {x})}$${\ Displaystyle T_ {x} N = \ ker (dg_ {x}).}$${\displaystyle df_{x}}$${\displaystyle dg_{x}}$${\ Displaystyle m (m-1)/2}$

${\ Displaystyle df_ {x} \ klin dg_ {x} = 0 \ w \ Lambda ^ {2} (T_ {x} ^ {*} M)}$

gdzie oznacza produkt zewnętrzny . Punkty stacjonarne są rozwiązaniami powyższego układu równań plus ograniczenie Należy zauważyć, że równania nie są niezależne, ponieważ lewa strona równania należy do podrozmaitości składających się z elementów rozkładających się . ${\ Displaystyle \ klin}$${\displaystyle x}$${\ Displaystyle g (x) = 0.}$${\displaystyle {\tfrac {1}{2}}m(m-1)}$${\ Displaystyle \ Lambda ^ {2} (T_ {x} ^ {*} M)}$

W tym sformułowaniu nie jest konieczne jednoznaczne znalezienie mnożnika Lagrange'a, liczby takiej, że${\ Displaystyle \ lambda}$${\ Displaystyle df_ {x} = \ lambda \, dg_ {x}.}$

Wiele ograniczeń

Niech i bądź jak w powyższej sekcji dotyczącej przypadku pojedynczego ograniczenia. Zamiast funkcji tam opisanej rozważmy teraz funkcję gładką z funkcjami składowymi, dla których jest wartością regularną . Niech będzie podrozmaitością zdefiniowanego przez${\ Displaystyle M}$${\displaystyle f}$${\displaystyle g}$${\ Displaystyle G: M \ do \ mathbb {R} ^ {p} (p> 1),}$${\ Displaystyle g_ {i}: M \ do \ mathbb {R} ,}$${\ Displaystyle 0 \ w \ mathbb {R} ^ {p}}$${\ Displaystyle N}$${\ Displaystyle M}$${\ Displaystyle G (x) = 0.}$

${\displaystyle x}$jest punktem stacjonarnym wtedy i tylko wtedy, gdy zawiera . Dla wygody pozwolić i , gdzie oznacza mapę styczna lub jakobian Podprzestrzeń ma wymiar mniejszy niż w przypadku , a mianowicie , a należący do wtedy i tylko wtedy, gdy należy z obrazem obliczeniowo biorąc, warunek, że należący do przestrzeni wierszy macierzy lub równoważnie przestrzeń kolumn macierzy (transpozycji). Jeżeli oznacza iloczyn zewnętrzny kolumn macierzy warunku stacjonarnego dla at staje się ${\ Displaystyle f | _ {N}}$${\ Displaystyle \ ker (df_ {x})}$${\ Displaystyle \ ker (dG_ {x})}$${\ Displaystyle L_ {x} = df_ {x}}$${\ Displaystyle K_ {x} = DG_ {x},}$${\displaystyle DG}$${\ Displaystyle TM \ do T \ mathbb {R} ^ {p}.}$${\ Displaystyle \ ker (K_ {x})}$${\ Displaystyle \ ker (L_ {x})}$${\ Displaystyle \ ciemny (\ ker (L_ {x})) = n-1}$${\ Displaystyle \ ciemny (\ ker (K_ {x})) = np.}$ ${\ Displaystyle \ ker (K_ {x})}$${\ Displaystyle \ ker (L_ {x})}$${\ Displaystyle L_ {x} \ w T_ {x} ^ {*} M}$${\ Displaystyle K_ {x} ^ {*}: \ mathbb {R} ^ {p *} \ do T_ {x} ^ {*} M.}$${\ Displaystyle L_ {x}}$${\ Displaystyle K_ {x},}$${\ Displaystyle K_ {x} ^ {*}}$${\ Displaystyle \ omega _ {x} \ w \ Lambda ^ {p} (T_ {x} ^ {*} M)}$${\ Displaystyle K_ {x} ^ {*},}$${\ Displaystyle f | _ {N}}$${\displaystyle x}$

${\ Displaystyle L_ {x} \ klin \ omega _ {x} = 0 \ w \ Lambda ^ {p + 1} \ lewo (T_ {x} ^ {*} M \ po prawej)}$

Ponownie, w tym sformułowaniu nie jest konieczne, aby jednoznacznie znaleźć mnożniki Lagrange'a, takie liczby , że ${\ Displaystyle \ lambda _ {1} \ ldots \ lambda _ {p}}$

${\ Displaystyle df_ {x} = \ suma _ {i = 1} ^ {p} \ lambda _ {i} d (g_ {i}) _ {x}.}$

Interpretacja mnożników Lagrange'a

Często mnożniki Lagrange'a są interpretowane jako pewna ilość zainteresowania. Na przykład poprzez parametryzację linii konturu ograniczenia, to znaczy, jeśli wyrażenie Lagrange'a to

${\ Displaystyle {\ zacząć {wyrównany} i {\ mathcal {L}} (x_ {1}, x_ {2}, \ ldots; \ lambda _ {1}, \ lambda _ {2}, \ ldots; c_ { 1},c_{2},\ldots )\\[4pt]={}&f(x_{1},x_{2},\ldots )+\lambda _{1}(c_{1}-g_{1 }(x_{1},x_{2},\ldots ))+\lambda _{2}(c_{2}-g_{2}(x_{1},x_{2},\dots ))+\ cdots \end{aligned}}}$

następnie

${\ Displaystyle {\ Frac {\ częściowy {\ mathcal {L}}} {\ częściowy c_ {k}}} = \ lambda _ {k}.}$

Tak więc λ _k jest szybkością zmian optymalizowanej wielkości w funkcji parametru ograniczenia. Jako przykłady, w mechanice Lagrange'a równania ruchu są wyprowadzane przez znalezienie stacjonarnych punktów działania , całki po czasie z różnicy między energią kinetyczną i potencjalną. Tak więc siła działająca na cząstkę ze względu na potencjał skalarny, F = −∇ V , może być interpretowana jako mnożnik Lagrange'a określający zmianę działania (przeniesienie potencjału na energię kinetyczną) po zmianie ograniczonej trajektorii cząstki. W teorii sterowania formułuje się to zamiast równań costate .

Co więcej, przez twierdzenie obwiedni optymalna wartość mnożnika Lagrange'a jest interpretowana jako marginalny wpływ odpowiedniej stałej ograniczającej na optymalną osiągalną wartość pierwotnej funkcji celu: jeśli oznaczymy wartości w optimum gwiazdką, to może pokazać, że

${\ Displaystyle {\ Frac {{\ tekst {d}} f (x_ {1} ^ {*} (c_ {1}, c_ {2}, \ kropki), x_ {2} ^ {*} (c_ { 1},c_{2},\dots ),\dots )}{{\text{d}}c_{k}}}=\lambda _{k}^{*}.}$

Na przykład w ekonomii optymalny zysk gracza jest obliczany przy ograniczonej przestrzeni działań, gdzie mnożnik Lagrange'a jest zmianą optymalnej wartości funkcji celu (zysku) ze względu na rozluźnienie danego ograniczenia (np. poprzez zmiana dochodu); w takim kontekście λ _k * jest kosztem krańcowym ograniczenia i jest określana jako cena w tle .

Wystarczające warunki

Wystarczające warunki dla ograniczonego lokalnego maksimum lub minimum można określić w postaci ciągu głównych małoletnich (wyznaczników górno-lewych uzasadnionych podmatryc) obramowanej macierzy Hessów drugich pochodnych wyrażenia Lagrange'a.

Przykłady

Przykład 1

Przykład 1a

Załóżmy, że chcemy zmaksymalizować z zastrzeżeniem ograniczenia . Możliwe zestaw jest okręgu jednostkowego, a ustawia poziom z F są ukośne linie (z nachylenia -1), dzięki czemu widać, że maksymalna graficznej pojawia się , a minimalna występuje przy . ${\ Displaystyle f (x, y) = x + y}$${\ Displaystyle x ^ {2} + Y ^ {2} = 1}$${\ Displaystyle \ lewo ({\ tfrac {1} {\ sqrt {2}}}, {\ tfrac {1} {\ sqrt {2}}} \ po prawej)}$${\ Displaystyle \ lewo (-{\ tfrac {1} {\ sqrt {2}}}, - {\ tfrac {1} {\ sqrt {2}}} \ prawej)}$

Dla metody mnożników Lagrange'a ograniczeniem jest

${\ Displaystyle g (x, y) = x ^ {2} + y ^ {2} -1 = 0,}$

W związku z tym

${\ Displaystyle {\ zacząć {wyrównany} {\ mathcal {L}} (x, y, \ lambda) i = f (x, y) + \ lambda \ cdot g (x, y) \ \ [4pt] i = x+y+\lambda (x^{2}+y^{2}-1).\end{wyrównany}}}$

funkcja równoważna funkcji when jest ustawiona na . ${\displaystyle f(x,y)}$${\displaystyle g(x,y)}$${\ Displaystyle 0}$

Teraz możemy obliczyć gradient:

${\ Displaystyle {\ zacząć {wyrównany} \ nabla _ {x, y, \ lambda} {\ mathcal {l}} (x, y, \ lambda) & = \ lewo ({\ frac {\ częściowy {\ mathcal { L}}}{\częściowy x}},{\frac {\częściowy {\mathcal {L}}}{\częściowy y}},{\frac {\częściowy {\mathcal {L}}}{\częściowy \ lambda }}\right)\\[4pt]&=\left(1+2\lambda x,1+2\lambda y,x^{2}+y^{2}-1\right)\end{aligned }}}$

i dlatego:

${\ Displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0 \ quad \ leftrightarrow \ quad {\ zacząć {przypadki} 1 + 2 \ lambda x = 0\\1+2\lambda y=0\\x^{2}+y^{2}-1=0\end{przypadki}}}$

Zauważ, że ostatnie równanie jest pierwotnym wiązaniem.

Pierwsze dwa równania dają

${\ Displaystyle x = y = - {\ Frac {1} {2 \ lambda}} \ qquad \ lambda \ neq 0.}$

Podstawiając do ostatniego równania otrzymujemy:

${\ Displaystyle {\ Frac {1} {4 \ Lambda ^ {2}}} + {\ Frac {1} {4 \ Lambda ^ {2}}} -1 = 0}$

więc

${\ Displaystyle \ lambda = \ pm {\ Frac {1} {\ sqrt {2}}},}$

co oznacza, że ​​stacjonarne punkty są ${\displaystyle {\mathcal {L}}}$

${\ Displaystyle \ lewo ({\ tfrac {\ sqrt {2}} {2}}, {\ tfrac {\ sqrt {2}} {2}}, - {\ tfrac {1} {\ sqrt {2}} }\right),\qquad \left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}},{\tfrac {1}{\ sqrt {2}}}\prawo).}$

Obliczanie funkcji celu f w tych punktach daje

${\ Displaystyle f \ lewo ({\ tfrac {\ sqrt {2}} {2}}, {\ tfrac {\ sqrt {2}} {2}} \ po prawej) = {\ sqrt {2}}, \ qquad f\left(-{\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right)=-{\sqrt {2}}.}$

Zatem ograniczone maksimum to i ograniczone minimum to . ${\displaystyle {\sqrt {2}}}$${\displaystyle -{\sqrt {2}}}$

Przykład 1b

Teraz modyfikujemy funkcję celu z przykładu 1a, aby zminimalizować zamiast ponownie wzdłuż okręgu . Teraz zestawy poziomów to nadal linie nachylenia -1, a punkty na okręgu styczne do tych zestawów poziomów to znowu i . Te punkty styczności to maksima  . ${\ Displaystyle f (x, y) = (x + y) ^ {2}}$${\displaystyle f(x,y)=x+y}$${\ Displaystyle g (x, y) = x ^ {2} + y ^ {2} -1 = 0}$${\displaystyle f}$${\ Displaystyle ({\ sqrt {2}}/2, {\ sqrt {2}}/2)}$${\ Displaystyle (-{\ sqrt {2}}/2, - {\ sqrt {2}}/2)}$${\displaystyle f}$

Z drugiej strony minima występują na poziomie ustawionym na  = 0 (ponieważ przez swoją konstrukcję nie może przyjmować wartości ujemnych), w i , gdzie krzywe poziomu nie są styczne do ograniczenia. Warunek, który poprawnie identyfikuje wszystkie cztery punkty jako ekstrema; minima charakteryzują się w szczególności:${\displaystyle f}$${\displaystyle f}$${\ Displaystyle ({\ sqrt {2}}/2, - {\ sqrt {2}}/2)}$${\ Displaystyle (-{\ sqrt {2}}/2, {\ sqrt {2}}/2)}$${\displaystyle f}$${\ Displaystyle \ nabla f = \ lambda \ \ nabla g}$${\ Displaystyle \ lambda = 0.}$

Przykład 2

Ten przykład dotyczy bardziej żmudnych obliczeń, ale nadal jest to problem z pojedynczym wiązaniem.

Załóżmy, że ktoś chce znaleźć maksymalne wartości

${\ Displaystyle f (x, y) = x ^ {2} y}$

pod warunkiem, że współrzędne - i - leżą na okręgu wokół początku o promieniu . To znaczy z zastrzeżeniem ograniczenia ${\displaystyle x}$${\displaystyle y}$${\displaystyle {\sqrt {3}}}$

${\ Displaystyle g (x, y) = x ^ {2} + y ^ {2} -3 = 0.}$

Ponieważ istnieje tylko jedno ograniczenie, istnieje jeden mnożnik, powiedzmy . ${\ Displaystyle \ lambda}$

Ograniczenie ma identyczne zero na okręgu o promieniu . Dowolna wielokrotność może zostać dodana do pozostawienia niezmienionego w obszarze zainteresowania (w okręgu, w którym spełnione jest nasze pierwotne ograniczenie). ${\displaystyle g(x,y)}$${\displaystyle {\sqrt {3}}}$${\displaystyle g(x,y)}$${\displaystyle g(x,y)}$${\displaystyle g(x,y)}$

Zastosowanie zwykłej metody mnożnikowej Lagrange'a daje

${\ Displaystyle {\ zacząć {wyrównany} {\ mathcal {L}} (x, y, \ lambda) i = f (x, y) + \ lambda \ cdot g (x, y) \ \ i = x ^ { 2}y+\lambda (x^{2}+y^{2}-3).\end{wyrównany}}}$

z którego można obliczyć gradient:

${\ Displaystyle {\ zacząć {wyrównany} \ nabla _ {x, y, \ lambda} {\ mathcal {l}} (x, y, \ lambda) & = \ lewo ({\ frac {\ częściowy {\ mathcal { L}}}{\częściowy x}},{\frac {\częściowy {\mathcal {L}}}{\częściowy y}},{\frac {\częściowy {\mathcal {L}}}{\częściowy \ lambda }}\right)\\&=\left(2xy+2\lambda x,x^{2}+2\lambda y,x^{2}+y^{2}-3\right).\end {wyrównany}}}$

I dlatego:

${\ Displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0 \ quad \ iff \ quad {\ zacząć {przypadki} 2xy + 2 \ lambda x = 0\\x^{2}+2\lambda y=0\\x^{2}+y^{2}-3=0\end{przypadki}}\quad \iff \quad {\begin{przypadki} x(y+\lambda )=0&{\text{(i)}}\\x^{2}=-2\lambda y&{\text{(ii)}}\\x^{2}+y^{ 2}=3&{\text{(iii)}}\end{przypadki}}}$

(iii) jest tylko pierwotnym ograniczeniem. (i) implikuje lub . Jeśli to przez (iii) iw konsekwencji z (ii). Jeśli , zastąpienie tego w (ii) daje . Zastąpienie tego w (iii) i rozwiązanie daje . Tak więc istnieje sześć punktów krytycznych : ${\ Displaystyle x = 0}$ ${\ Displaystyle \ lambda =-y}$${\ Displaystyle x = 0}$${\displaystyle y=\pm {\sqrt {3}}}$${\ Displaystyle \ lambda = 0}$${\ Displaystyle \ lambda =-y}$${\ Displaystyle x ^ {2} = 2 lata ^ {2}}$${\displaystyle y}$${\ Displaystyle y = \ pm 1}$${\displaystyle {\mathcal {L}}}$

${\displaystyle ({\sqrt {2}},1,-1);\quad (-{\sqrt {2}},1,-1);\quad ({\sqrt {2}},-1, 1);\quad (-{\sqrt {2}},-1,1);\quad (0,{\sqrt {3}},0);\quad (0,-{\sqrt {3}} ,0).}$

Oceniając cel w tych punktach, stwierdza się, że:

${\ Displaystyle f (\ pm {\ sqrt {2}}, 1) = 2; \ quad f (\ pm {\ sqrt {2}}, -1) = -2; \ quad f (0, \ pm { \sqrt {3}})=0.}$

W związku z tym, funkcja celu osiąga globalnym maksimum (w zależności od ograniczeń w) i globalne minimum w Punkt jest lokalne minimum w i jest lokalne maksimum z , które mogą być określone poprzez rozważenie Heskiego matrycy o . ${\ Displaystyle (\ pm {\ sqrt {2}}, 1)}$${\displaystyle (\pm {\sqrt {2}},-1).}$${\ Displaystyle (0, {\ sqrt {3}})}$${\displaystyle f}$${\ Displaystyle (0,-{\ sqrt {3}})}$${\displaystyle f}$${\displaystyle {\mathcal {L}}(x,y,0)}$

Zauważ, że chociaż jest punktem krytycznym , nie jest lokalnym ekstremum Mamy ${\displaystyle ({\sqrt {2}},1,-1)}$${\displaystyle {\mathcal {L}}}$${\displaystyle {\mathcal {L}}.}$

${\ Displaystyle {\ mathcal {L}} \ lewo ({\ sqrt {2}} + \ varepsilon, 1, 1 + \ delta \ po prawej) = 2 + \ delta \ po lewej (\ varepsilon ^ {2} + \ left(2{\sqrt {2}}\right)\varepsilon \right).}$

Mając dowolne sąsiedztwo , można wybrać małą wartość dodatnią i małą wartość dowolnego znaku, aby otrzymać wartości zarówno większe, jak i mniejsze niż . Można to również zobaczyć na podstawie macierzy Hessian ocenianej w tym punkcie (lub rzeczywiście w dowolnym z punktów krytycznych), która jest macierzą nieokreśloną . Każdy z punktów krytycznych to punkt siodłowy z . ${\displaystyle ({\sqrt {2}},1,-1)}$${\displaystyle \varepsilon}$${\ Displaystyle \ delta}$${\displaystyle {\mathcal {L}}}$${\displaystyle 2}$${\displaystyle {\mathcal {L}}}$${\displaystyle {\mathcal {L}}}$${\displaystyle {\mathcal {L}}}$

Przykład 3: Entropia

Załóżmy, że chcemy znaleźć dyskretny rozkład prawdopodobieństwa w punktach o maksymalnej entropii informacyjnej . To to samo, co powiedzenie, że chcemy znaleźć najmniej ustrukturyzowany rozkład prawdopodobieństwa na punktach . Innymi słowy, chcemy zmaksymalizować równanie entropii Shannona : ${\displaystyle \{p_{1},p_{2},\ldots,p_{n}\}}$${\displaystyle \{p_{1},p_{2},\cdots,p_{n}\}}$

${\ Displaystyle f (p_ {1}, p_ {2}, \ ldots, p_ {n}) = - \ suma _ {j = 1} ^ {n} p_ {j} \ log _ {2} p_ {j }.}$

Aby był to rozkład prawdopodobieństwa, suma prawdopodobieństw w każdym punkcie musi być równa 1, więc nasze ograniczenie jest następujące: ${\displaystyle p_{i}}$${\displaystyle x_{i}}$

${\ Displaystyle g (p_ {1}, p_ {2}, \ ldots, p_ {n}) = \ suma _ {j = 1} ^ {n} p_ {j} = 1.}$

Używamy mnożników Lagrange'a, aby znaleźć punkt maksymalnej entropii, , we wszystkich dyskretnych rozkładach prawdopodobieństwa na . Wymagamy, aby: ${\ Displaystyle {\ vec {p}} ^ {\, *}}$${\displaystyle {\vec {p}}}$${\ Displaystyle \ {x_ {1}, x_ {2}, \ ldots, x_ {n} \}}$

${\ Displaystyle \ lewo. {\ Frac {\ częściowy} {\ częściowy {\ vec {p}}}} (f + \ lambda (g-1)) \ prawo | _ {{\ vec {p}} = {\ vec {p}}^{\,*}}=0,}$

co daje układ n równań , taki, że: ${\displaystyle k=1,\ldots,n}$

${\ Displaystyle \ lewo. {\ Frac {\ częściowy} {\ częściowy p_ {k}}} \ lewo \ {- \ lewo (\ suma _ {j = 1} ^ {n} p_ {j} \ log _ { 2}p_{j}\right)+\lambda \left(\sum _{j=1}^{n}p_{j}-1\right)\right\}\right|_{p_{k}= p_{k}^{*}}=0.}$

Dokonując różniczkowania tych n równań otrzymujemy

${\ Displaystyle - \ lewo ({\ Frac {1} {\ ln 2}} + \ log _ {2} p_ {k} ^ {*} \ prawej) + \ lambda = 0.}$

To pokazuje, że wszystkie są równe (ponieważ zależą tylko od λ ). Używając ograniczenia ${\ Displaystyle p_ {k} ^ {*}}$

${\ Displaystyle \ suma _ {j} p_ {j} = 1,}$

znaleźliśmy

${\ Displaystyle p_ {k} ^ {*} = {\ Frac {1} {n}}.}$

Stąd rozkład jednostajny jest rozkładem o największej entropii wśród rozkładów na n punktach.

Przykład 4: Optymalizacja numeryczna

Punkty krytyczne Lagrange'ów występują w punktach siodłowych , a nie w lokalnych maksimach (lub minimach). Niestety, wiele technik optymalizacji numerycznej, takich jak wspinaczka górska , zejście gradientowe , niektóre z metod quasi-Newtonowych , między innymi, są przeznaczone do znajdowania lokalnych maksimów (lub minimów), a nie punktów siodłowych. Z tego powodu należy albo zmodyfikować formułę, aby upewnić się, że jest to problem minimalizacji (na przykład przez ekstremizację kwadratu gradientu Lagrange'a jak poniżej), albo użyć techniki optymalizacji, która znajduje punkty stacjonarne (takich jak metoda Newtona bez ekstremum szukającego linii wyszukiwania ) i niekoniecznie ekstrema.

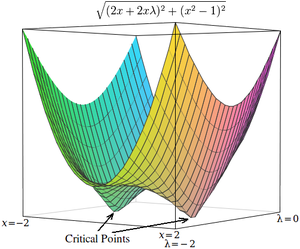
Jako prosty przykład rozważmy problem znalezienia wartości x, która minimalizuje , ograniczona tak, że . (Ten problem jest nieco patologiczny, ponieważ istnieją tylko dwie wartości, które spełniają to ograniczenie, ale jest to przydatne do celów ilustracyjnych, ponieważ odpowiadającą mu funkcję nieograniczoną można zwizualizować w trzech wymiarach). ${\ Displaystyle f (x) = x ^ {2}}$${\ Displaystyle x ^ {2} = 1}$

Używając mnożników Lagrange'a, problem ten można przekształcić w nieograniczony problem optymalizacji:

${\ Displaystyle {\ mathcal {L}} (x \ lambda) = x ^ {2} + \ lambda (x ^ {2}-1).}$

Dwa punkty krytyczne występują w punktach siodłowych, gdzie x = 1 i x = -1 .

Aby rozwiązać ten problem za pomocą techniki optymalizacji numerycznej, musimy najpierw przekształcić ten problem tak, aby punkty krytyczne występowały w lokalnych minimach. Odbywa się to poprzez obliczenie wielkości gradientu problemu optymalizacji nieograniczonej.

Najpierw obliczamy pochodną cząstkową problemu nieograniczonego względem każdej zmiennej:

${\ Displaystyle {\ zacząć {wyrównany} i {\ Frac {\ częściowy {\ matematyczny {L}}} {\ częściowy x}} = 2 x + 2 x \ lambda \ \ [5 pkt] i {\ Frac {\ częściowy {\ mathcal {L}}}{\częściowa \lambda }}=x^{2}-1.\end{aligned}}}$

Jeżeli funkcja celu nie jest łatwo różniczkowalna, różniczka względem każdej zmiennej może być aproksymowana jako

${\ Displaystyle {\ zacząć {wyrównany} {\ Frac {\ częściowy {\ mathcal {l}}}{\ częściowy x}} \ około {\ Frac {{\ mathcal {l}} (x + \ varepsilon \ lambda) -{\mathcal {L}}(x,\lambda )}{\varepsilon }},\\[5pt]{\frac {\partial {\mathcal {L}}}{\częściowy \lambda }}\ok { \frac {{\mathcal {L}}(x,\lambda +\varepsilon )-{\mathcal {L}}(x,\lambda )}{\varepsilon }},\end{wyrównany}}}$

gdzie jest mała wartość. ${\displaystyle \varepsilon}$

Następnie obliczamy wielkość gradientu, który jest pierwiastkiem kwadratowym z sumy kwadratów pochodnych cząstkowych:

${\ Displaystyle {\ zacząć {wyrównany} h (x \ lambda) i = {\ sqrt {(2x + 2 x \ lambda) ^ {2} + (x ^ {2}-1) ^ {2}}} \ \[4pt]&\ok {\sqrt {\left({\frac {{\mathcal {L}}(x+\varepsilon ,\lambda )-{\mathcal {L}}(x,\lambda )}{\ varepsilon }}\right)^{2}+\left({\frac {{\mathcal {L}}(x,\lambda +\varepsilon )-{\mathcal {L}}(x,\lambda )}{ \varepsilon }}\right)^{2}}}.\end{aligned}}}$

(Ponieważ moduł jest zawsze nieujemny, optymalizacja pod względem kwadratu jest równoważna optymalizacji pod modułem. W związku z tym „pierwiastek kwadratowy” można pominąć w tych równaniach bez oczekiwanej różnicy w wynikach optymalizacji).

Punkty krytyczne h występują przy x = 1 i x = −1 , tak jak w . Jednak w przeciwieństwie do punktów krytycznych w , punkty krytyczne w h występują na lokalnych minimach, więc do ich znalezienia można użyć technik optymalizacji numerycznej. ${\displaystyle {\mathcal {L}}}$${\displaystyle {\mathcal {L}}}$

Aplikacje

Teoria kontroli

W teorii kontroli optymalnej mnożniki Lagrange'a są interpretowane jako zmienne brzegowe , a mnożniki Lagrange'a są przeformułowane jako minimalizacja hamiltonianu zgodnie z zasadą minimum Pontryagina .

Programowanie nieliniowe

Metoda mnożnika Lagrange'a ma kilka uogólnień. W programowaniu nieliniowym istnieje kilka reguł mnożnikowych, np. Carathéodory-John Multiplier Rule i Convex Multiplier Rule, dla ograniczeń nierówności.

Systemy zasilania

Metody oparte na mnożnikach Lagrange'a mają zastosowanie w systemach elektroenergetycznych , np. w rozmieszczaniu rozproszonych zasobów energii (DER) i zrzucaniu obciążenia.

Zobacz też

Bibliografia

Dalsza lektura

• Beavis, Brian; Dobbs, Ian M. (1990). „Optymalizacja statyczna” . Teoria optymalizacji i stabilności w analizie ekonomicznej . Nowy Jork: Cambridge University Press. s. 32-72. Numer ISBN 0-521-33605-8.
• Bertsekas, Dimitri P. (1982). Optymalizacja z ograniczeniami i metody mnożnika Lagrange'a . Nowy Jork: prasa akademicka. Numer ISBN 0-12-093480-9.
• Beveridge, Gordon SG; Schechter, Robert S. (1970). „Mnożniki Lagrange'a” . Optymalizacja: teoria i praktyka . Nowy Jork: McGraw-Hill. s. 244-259. Numer ISBN 0-07-005128-3.
• Binger, Brian R.; Hoffman, Elżbieta (1998). „Ograniczona optymalizacja”. Mikroekonomia z rachunkiem (wyd. 2). Czytanie: Addison-Wesley. s. 56–91. Numer ISBN 0-321-01225-9.
• Carter, Michael (2001). „Ograniczenia równości” . Podstawy ekonomii matematycznej . Cambridge: MIT Press. s. 516-549. Numer ISBN 0-262-53192-5.
• Hestenes, Magnus R. (1966). „Minima funkcji podlegających ograniczeniom równości”. Rachunek wariacyjny i teoria kontroli optymalnej . Nowy Jork: Wiley. s. 29–34.
• Wylie, C. Ray; Barrett, Louis C. (1995). „Ekstrema całki pod ograniczeniem”. Zaawansowana matematyka inżynierska (wyd. szóste). Nowy Jork: McGraw-Hill. s. 1096-1103. Numer ISBN 0-07-072206-4.

Zewnętrzne linki

Ekspozycja

• blog kipida - Metoda mnożników Lagrange'a
• Wprowadzenie koncepcyjne (plus krótkie omówienie mnożników Lagrange'a w rachunku wariacyjnym stosowanym w fizyce)
• Mnożniki Lagrange'a dla form kwadratowych z ograniczeniami liniowymi autorstwa Kennetha H. Carpentera

Dodatkowy tekst i interaktywne aplety

• Proste wyjaśnienie na przykładzie rządów stosujących podatki jako mnożniki Lagrange'a
• Mnożniki Lagrange'a bez trwałego wyjaśnienia blizn z naciskiem na intuicję Dana Kleina
• Geometryczna reprezentacja metody mnożników Lagrange'a Zapewnia przekonujący wgląd w 2 wymiarach, że w punkcie minimalizacji kierunek najbardziej stromego opadania musi być prostopadły do ​​stycznej krzywej ograniczenia w tym punkcie. [Wymaga InternetExplorer/Firefox/Safari] Demonstracja Mathematica autorstwa Shashi Sathyanarayana
• Aplet
• MIT OpenCourseware Wykład wideo na temat mnożników Lagrange'a z kursu rachunku różniczkowego wielu zmiennych
• Slajdy towarzyszące tekstowi optymalizacji nieliniowej Bertsekasa , ze szczegółami dotyczącymi mnożników Lagrange'a (wykłady 11 i 12)
• Geometryczna idea mnożników Lagrange'a
• MATLAB przykład wykorzystania mnożników Lagrange'a w optymalizacji