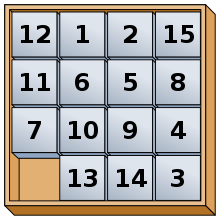
15 puzzli - 15 puzzle

Aby rozwiązać zagadkę, liczby muszą być uporządkowane w kolejności

15 puzzle (zwany również Gem logiczne , Boss logiczne , gry Piętnastki , Mystic Square i wielu innych) jest przesuwane puzzle mając 15 kwadratowe płytki o numerach 1-15 w ramce, która jest wysoki i 4 płytki o szerokości 4 płytki, pozostawiając jedną niezajęta położenie płytek. Płytki w tym samym rzędzie lub kolumnie w pozycji otwartej można przesuwać, przesuwając je odpowiednio w poziomie lub w pionie. Celem łamigłówki jest ułożenie płytek w kolejności numerycznej.

Nazwana ze względu na liczbę płytek w ramce, 15 łamigłówka może być również nazywana łamigłówką 16, co odnosi się do całkowitej pojemności płytek. Podobne nazwy są używane dla różnych rozmiarów wariantów układanki 15, takich jak układanka 8, która ma 8 płytek w ramce 3×3.

N logiczna jest klasycznym problemem modelowania algorytmów udziałem heurystyczne . Powszechnie stosowana heurystyka dla tego problemu obejmuje liczenie liczby źle umieszczonych płytek i znajdowanie sumy odległości taksówek między każdym blokiem i jego pozycją w konfiguracji celu. Zauważ, że oba są dopuszczalne , tzn. nigdy nie przeceniają liczby pozostałych ruchów, co zapewnia optymalność dla niektórych algorytmów wyszukiwania, takich jak A* .

Matematyka

Rozwiązalność

15 rozwiązanych zagadek

Johnson i Story (1879) użyli argumentu parzystości, aby pokazać, że połowa pozycji początkowych dla łamigłówki n jest niemożliwa do rozwiązania, niezależnie od liczby wykonanych ruchów. Odbywa się to poprzez rozważenie funkcji konfiguracji kafelków, która jest niezmienna w każdym prawidłowym ruchu, a następnie użycie tego do podzielenia przestrzeni wszystkich możliwych stanów oznaczonych na dwie klasy równoważności stanów osiągalnych i nieosiągalnych.

Niezmiennikiem jest parzystość permutacji wszystkich 16 kwadratów plus parzystość odległości taksówki (liczba rzędów plus liczba kolumn) pustego kwadratu od prawego dolnego rogu. Jest to niezmiennik, ponieważ każdy ruch zmienia zarówno parzystość permutacji, jak i parzystość odległości taksówki. W szczególności, jeśli puste pole znajduje się w prawym dolnym rogu, łamigłówkę można rozwiązać wtedy i tylko wtedy, gdy permutacja pozostałych elementów jest parzysta.

Johnson i historia (1879) pokazał, że odwrotna posiada na płytkach o rozmiarze m x n przewidzianego m i n są jak co najmniej 2: wszystkie parzyste permutacji jest rozpuszczalny. Jest to proste, ale trochę niechlujne do udowodnienia przez indukcję na m i n, zaczynając od m = n =2. Archer (1999) podał kolejny dowód, oparty na zdefiniowaniu klas równoważności za pomocą ścieżki hamiltonowskiej .

Wilson (1974) badał uogólnienie łamigłówki 15 na dowolne grafy skończone , przy czym pierwotnym problemem był przypadek grafu siatkowego 4×4 . Problem ma kilka zdegenerowanych przypadków, w których odpowiedź jest albo trywialna, albo prosta kombinacja odpowiedzi na ten sam problem na niektórych podgrafach. Mianowicie, dla ścieżek i wielokątów łamigłówka nie ma swobody; jeśli graf jest rozłączony , istotny jest tylko spójny składnik wierzchołka z „pustą przestrzenią”; a jeśli istnieje wierzchołek artykulacji, problem sprowadza się do tej samej układanki na każdym z dwóch połączonych elementów tego wierzchołka. Wyłączając te przypadki, Wilson wykazał, że poza jednym wyjątkowym grafem na 7 wierzchołkach, możliwe jest otrzymanie wszystkich permutacji, chyba że graf jest dwudzielny , w którym to przypadku można uzyskać dokładnie parzyste permutacje. Wyjątkowy wykres to sześciokąt foremny z dodaną jedną przekątną i wierzchołkiem w środku; tylko1/6 z jego permutacji można osiągnąć.

W przypadku większych wersji łamigłówki n znalezienie rozwiązania jest łatwe, ale problem znalezienia najkrótszego rozwiązania jest NP-trudny . NP jest również trudne do aproksymacji najmniejszej liczby slajdów w ramach stałej addytywnej, ale istnieje aproksymacja wielomianowego współczynnika stałej czasowej. W przypadku 15 puzzli długości optymalnych rozwiązań wahają się od 0 do 80 ruchów pojedynczych płytek (jest 17 konfiguracji wymagających 80 ruchów) lub 43 ruchów na wiele płytek; 8 łamigłówkę zawsze można rozwiązać w nie więcej niż 31 ruchach pojedynczych płytek lub 24 ruchach wielu płytek (sekwencja liczb całkowitych A087725 ). Metryka wielu płytek liczy kolejne ruchy pustej płytki w tym samym kierunku, co jeden.

Liczba możliwych pozycji 24 puzzli to 25!/2 ≈ 7,76 × 10 ^24, czyli za dużo, aby obliczyć liczbę Bożą . W 2011 r. ustalono dolne granice 152 ruchów pojedynczych płytek lub 41 ruchów wielopłytkowych, a także górne granice 208 ruchów pojedynczych płytek lub 109 ruchów wielopłytkowych. W 2016 r. górna granica została poprawiona do 205 ruchów pojedynczych płytek.

Przekształcenia piętnastu puzzli tworzą groupoid (nie grupę, ponieważ nie wszystkie ruchy można skomponować); ten groupoid działa na konfiguracjach.

Teoria grup

Ponieważ kombinacje 15 puzzli mogą być generowane przez 3 cykle , można udowodnić, że 15 puzzli może być reprezentowana przez grupę naprzemienną . W rzeczywistości każdą przesuwaną łamigłówkę z kwadratowymi płytkami o tym samym rozmiarze można przedstawić za pomocą . ${\ Displaystyle A_ {15}}$${\ Displaystyle 2k-1}$${\ Displaystyle A_ {2k-1}}$

Dowód alternatywny

W innym ujęciu problemu, niezmiennik możemy uznać za sumę parzystości liczby inwersji w bieżącej kolejności 15 ponumerowanych elementów i parzystości różnicy w numerze wiersza pustego kwadratu z numer wiersza ostatniego wiersza. (Nazwijmy to odległością wiersza od ostatniego wiersza.) Jest to niezmiennik, ponieważ ruch każdej kolumny, gdy przesuwamy element w tej samej kolumnie, zmienia zarówno parzystość liczby inwersji (zmieniając liczbę inwersji o ±1 , ±3) i parzystość odległości rzędu od ostatniego rzędu (zmiana odległości rzędu ±1); a każdy ruch rzędu, kiedy poruszamy pionkiem w tym samym rzędzie, nie zmienia żadnej z dwóch parzystości. Teraz, jeśli spojrzymy na rozwiązany stan łamigłówki, ta suma jest parzysta. Stąd łatwo jest wykazać przez indukcję, że żaden stan układanki, dla którego powyższa suma jest nieparzysta, nie może być rozwiązany. W szczególności, jeśli pusty kwadrat znajduje się w prawym dolnym rogu (nawet w dowolnym miejscu w ostatnim rzędzie), to łamigłówkę można rozwiązać wtedy i tylko wtedy, gdy liczba inwersji ponumerowanych elementów jest parzysta.

Historia

Nierozwiązalna 15 łamigłówka Sama Loyda , z wymienionymi płytkami 14 i 15. Ta łamigłówka nie jest rozwiązana, ponieważ wymagałaby zmiany niezmiennika, aby przenieść ją do stanu rozwiązania.

Amerykański polityczny rysunek o znalezieniu republikańskiego kandydata na prezydenta w 1880 r.

Układanka została „wymyślona” przez Noyesa Palmera Chapmana, poczmistrza w Canastota w stanie Nowy Jork , który podobno pokazał znajomym już w 1874 roku prekursorską układankę składającą się z 16 ponumerowanych klocków, które miały być ułożone w rzędy po cztery , każdy sumując się do 34 . Kopie ulepszonej Piętnastej Zagadki trafiły do Syracuse w stanie Nowy Jork przez syna Noyesa, Franka, a stamtąd, poprzez różne połączenia, do Watch Hill na Rhode Island i wreszcie do Hartford (Connecticut), gdzie studenci American School dla Głuchych rozpoczęła produkcję zagadkę, a do grudnia 1879 roku, sprzedając je zarówno lokalnie, jak i w Bostonie , Massachusetts. Pokazano jeden z nich, Matthias Rice, który prowadził w Bostonie interesującą firmę zajmującą się obróbką drewna, rozpoczął produkcję puzzli w grudniu 1879 roku i przekonał sprzedawcę fantazyjnych towarów „Yankee Notions” do sprzedawania ich pod nazwą „Gem Puzzle”. Pod koniec stycznia 1880 roku dr Charles Pevey, dentysta z Worcester w stanie Massachusetts , zwrócił na siebie uwagę, oferując nagrodę pieniężną za rozwiązanie zagadki piętnastu.

Gra stała się szaleństwem w USA w 1880 roku.

Noyes Chapman złożył wniosek o patent na swój „Block Solitaire Puzzle” 21 lutego 1880 r. Jednak patent ten został odrzucony, prawdopodobnie dlatego, że nie różnił się wystarczająco od patentu „Puzzle-Blocks” z 20 sierpnia 1878 r. (US 207124). przyznane Ernestowi U. Kinsey.

Sam Loyd

Ilustracja Sama Loyda z 1914 r. przedstawiająca nierozwiązywalną wariację

Sam Loyd twierdził od 1891 aż do śmierci w 1911, że wynalazł zagadkę, na przykład pisząc w Cyclopedia of Puzzles (opublikowanej w 1914): „Starsi mieszkańcy Puzzleland będą pamiętać, jak na początku lat siedemdziesiątych doprowadzałem cały świat do szaleństwa z powodu małe pudełko z ruchomymi elementami, które stało się znane jako „Puzzle 14-15”. Jednak Loyd nie miał nic wspólnego z wynalezieniem lub początkową popularnością układanki, aw każdym razie szał nastąpił w 1880 roku, a nie na początku lat 70. XIX wieku. Pierwszy artykuł Loyda o zagadce został opublikowany w 1886 roku i dopiero w 1891 roku po raz pierwszy twierdził, że jest wynalazcą.

Późniejsze zainteresowanie podsyciło Loyd, który zaoferował nagrodę w wysokości 1000 USD dla każdego, kto mógłby zapewnić rozwiązanie pozwalające uzyskać konkretną kombinację określoną przez Loyda, a mianowicie odwrócić liczbę 14 i 15, nazywaną przez Loyda układanką 14-15 . Było to niemożliwe, jak pokazali ponad dekadę wcześniej Johnson & Story (1879) , ponieważ wymagało przekształcenia permutacji parzystych w nieparzyste.

Różnorodny

Minus Cube , produkowany w ZSRR , to 3D puzzle z podobnych operacji do 15 puzzle.

Bobby Fischer był ekspertem w rozwiązywaniu 15-Puzzle. Miał czas na rozwiązanie go w ciągu 25 sekund; Fischer zademonstrował to 8 listopada 1972 roku w The Tonight Show z udziałem Johnny'ego Carsona .

Zobacz też

• Zagadki kombinowane
• Jeu de taquin , operacja na skosie Younga, podobna do ruchów puzzli 15
• Kłocki
• Zagadki mechaniczne
• Problemy z ruchem kamyków
• Kostka Rubika
• Problem z trzema filiżankami

Uwagi

Bibliografia

Zewnętrzne linki

• Historia 15 puzzli
• Piętnaście łamigłówek
• Maksymalna liczba ruchów potrzebnych do uogólnienia m X n łamigłówki 15
• 15-Puzzle Optimal Solver z pobraniem (od Herberta Kociemby)