Sumy każdego wiersza, kolumny i głównych przekątnych są równe

Najmniejszy (i unikalny
aż do obrotu i odbicia) nietrywialny przypadek magicznego kwadratu, rząd 3
W matematyce rekreacyjnej kwadratowa tablica liczb, zwykle dodatnich liczb całkowitych , nazywana jest magicznym kwadratem, jeśli sumy liczb w każdym rzędzie, każdej kolumnie i obu głównych przekątnych są takie same. Zamówienie kwadratu magicznego jest liczba liczb wzdłuż jednego boku ( n ), a suma stałej nazywany jest stałą magia . Jeśli tablica zawiera tylko dodatnie liczby całkowite , mówimy, że magiczny kwadrat jest normalny . Niektórzy autorzy uważają, że magiczny kwadrat oznacza normalny magiczny kwadrat.

Magiczne kwadraty, które zawierają powtarzające się wpisy, nie podlegają tej definicji i są określane jako trywialne . Niektóre znane przykłady, w tym magiczny plac Sagrada Família i plac Parkera, są w tym sensie trywialne. Gdy wszystkie wiersze i kolumny, ale nie obie przekątne, sumują się do stałej magicznej, otrzymujemy półmagiczne kwadraty (czasami nazywane kwadratami ortomagicznymi ).
Matematyczne badanie magicznych kwadratów zwykle zajmuje się ich konstrukcją, klasyfikacją i wyliczaniem. Chociaż nie istnieją całkowicie ogólne metody tworzenia wszystkich magicznych kwadratów wszystkich rzędów, historycznie odkryto trzy ogólne techniki: metodą graniczną, przez tworzenie złożonych magicznych kwadratów i przez dodanie dwóch wstępnych kwadratów. Istnieją również bardziej szczegółowe strategie, takie jak metoda ciągłego wyliczania, która odtwarza określone wzorce. Magiczne kwadraty są generalnie klasyfikowane według kolejności n jako: nieparzyste, jeśli n jest nieparzyste, parzyste (określane również jako „podwójnie parzyste”), jeśli n jest wielokrotnością 4, dziwnie parzyste (znane również jako „pojedynczo parzyste”), jeśli n to dowolna inna liczba parzysta. Ta klasyfikacja opiera się na różnych technikach wymaganych do skonstruowania nieparzystych, parzystych i dziwnie parzystych kwadratów. Oprócz tego, w zależności od dalszych właściwości, magiczne kwadraty są również klasyfikowane jako asocjacyjne magiczne kwadraty , pandiagonalne magiczne kwadraty , najdoskonalsze magiczne kwadraty i tak dalej. Co trudniejsze, podjęto również próby sklasyfikowania wszystkich magicznych kwadratów danego rzędu jako przekształceń mniejszego zestawu kwadratów. Z wyjątkiem n ≤ 5, wyliczanie magicznych kwadratów wyższego rzędu jest nadal otwartym wyzwaniem. Wyliczenie najdoskonalszych magicznych kwadratów dowolnego rzędu zostało dokonane dopiero pod koniec XX wieku.
Magiczne kwadraty mają długą historię, sięgającą co najmniej 190 p.n.e. w Chinach. W różnych czasach nabierały znaczenia okultystycznego lub mitycznego i pojawiały się jako symbole w dziełach sztuki. W dzisiejszych czasach uogólniono je na wiele sposobów, w tym za pomocą dodatkowych lub różnych ograniczeń, mnożenie zamiast dodawania komórek, używanie alternatywnych kształtów lub więcej niż dwóch wymiarów oraz zastępowanie liczb kształtami i dodawanie operacjami geometrycznymi.

Dürera „s
melancholia i (1514) zawiera uporządkowaniu 4 kwadrat magicznym sumie 34
Historia
Magiczny kwadrat trzeciego rzędu był znany chińskim matematykom już w 190 r. p.n.e. i został wyraźnie podany w pierwszym stuleciu naszej ery. Pierwsze dające się datować wystąpienie magicznego kwadratu czwartego rzędu miało miejsce w 587 r. n.e. w Indiach. Okazy magicznych kwadratów rzędu 3 do 9 pojawiają się w encyklopedii z Bagdadu ok. 983 , Encyklopedia Braci Czystości ( Rasa'il Ikhwan al-Safa ). Pod koniec XII wieku ogólne metody konstruowania magicznych kwadratów były dobrze ugruntowane. Mniej więcej w tym czasie niektóre z tych kwadratów były coraz częściej używane w połączeniu z magicznymi literami, jak w Shams Al-ma'arif , do celów okultystycznych. W Indiach wszystkie kwadraty pandiagonalne czwartego rzędu zostały wyliczone przez Narayana w 1356 roku. rozwój sytuacji w Chinach, Indiach i na Bliskim Wschodzie. Godne uwagi są również starożytne kultury z tradycją matematyki i numerologii, które nie odkryły magicznych kwadratów: Grecy, Babilończycy, Egipcjanie i Amerykanie prekolumbijscy.
Chiny

Strona przedstawiająca magiczny kwadrat 9×9 z
Suanfa tongzong Cheng Dawei (1593).
Podczas gdy starożytne odniesienia do wzoru liczb parzystych i nieparzystych w magicznym kwadracie 3×3 pojawiają się w I Ching , pierwszy jednoznaczny przypadek tego magicznego kwadratu pojawia się w rozdziale zatytułowanym Mingtang (Jasna Sala) w księdze z I wieku Da Dai Liji (Zapis obrzędów Starszego Dai), który miał opisywać starożytne chińskie obrzędy dynastii Zhou. Liczby te występują również w prawdopodobnie wcześniejszym tekście matematycznym zwanym Shushu jiyi (Pamiętnik o niektórych tradycjach sztuki matematycznej), który został napisany w 190 r. p.n.e. Jest to najwcześniejsze odnotowane pojawienie się magicznego kwadratu; i był używany głównie do wróżbiarstwa i astrologii. Magiczny kwadrat 3×3 był określany przez wcześniejszych chińskich matematyków jako „Dziewięć Sal”. Identyfikacja magicznego kwadratu 3×3 z legendarnym wykresem Luoshu została dokonana dopiero w XII wieku, po czym nazwano go kwadratem Luoshu. Najstarszym zachowanym chiński traktat, który wyświetla magiczne kwadraty celu większej niż 3 Yang Hui „s Xugu zheqi suanfa (Kontynuacja starożytnych Metod Matematycznych dla wyjaśnienia dziwnych) napisanej w 1275 treścią traktatu Yang Hui zebrano od starszych prac, zarówno rodzimy i obcy; i wyjaśnia jedynie budowę magicznych kwadratów trzeciego i czwartego rzędu, przekazując jedynie gotowe diagramy większych kwadratów. Daje magiczny kwadrat rzędu 3, dwa kwadraty dla każdego rzędu 4 do 8, jeden rzędu 9 i jeden półmagiczny kwadrat rzędu 10. Daje również sześć magicznych kręgów o różnej złożoności.
|
|
| 2 |
16 |
13 |
3
|
| 11 |
5 |
8 |
10
|
| 7 |
9 |
12 |
6
|
| 14 |
4 |
1 |
15
|
|
| 1 |
23 |
16 |
4 |
21
|
| 15 |
14 |
7 |
18 |
11
|
| 24 |
17 |
13 |
9 |
2
|
| 20 |
8 |
19 |
12 |
6
|
| 5 |
3 |
10 |
22 |
25
|
|
| 13 |
22 |
18 |
27 |
11 |
20
|
| 31 |
4 |
36 |
9 |
29 |
2
|
| 12 |
21 |
14 |
23 |
16 |
25
|
| 30 |
3 |
5 |
32 |
34 |
7
|
| 17 |
26 |
10 |
19 |
15 |
24
|
| 8 |
35 |
28 |
1 |
6 |
33
|
|
| 46 |
8 |
16 |
20 |
29 |
7 |
49
|
| 3 |
40 |
35 |
36 |
18 |
41 |
2
|
| 44 |
12 |
33 |
23 |
19 |
38 |
6
|
| 28 |
26 |
11 |
25 |
39 |
24 |
22
|
| 5 |
37 |
31 |
27 |
17 |
13 |
45
|
| 48 |
9 |
15 |
14 |
32 |
10 |
47
|
| 1 |
43 |
34 |
30 |
21 |
42 |
4
|
|
| 61 |
3 |
2 |
64 |
57 |
7 |
6 |
60
|
| 12 |
54 |
55 |
9 |
16 |
50 |
51 |
13
|
| 20 |
46 |
47 |
17 |
24 |
42 |
43 |
21
|
| 37 |
27 |
26 |
40 |
33 |
31 |
30 |
36
|
| 29 |
35 |
34 |
32 |
25 |
39 |
38 |
28
|
| 44 |
22 |
23 |
41 |
48 |
18 |
19 |
45
|
| 52 |
14 |
15 |
49 |
56 |
10 |
11 |
53
|
| 5 |
59 |
58 |
8 |
1 |
63 |
62 |
4
|
|
| 31 |
76 |
13 |
36 |
81 |
18 |
29 |
74 |
11
|
| 22 |
40 |
58 |
27 |
45 |
63 |
20 |
38 |
56
|
| 67 |
4 |
49 |
72 |
9 |
54 |
65 |
2 |
47
|
| 30 |
75 |
12 |
32 |
77 |
14 |
34 |
79 |
16
|
| 21 |
39 |
57 |
23 |
41 |
59 |
25 |
43 |
61
|
| 66 |
3 |
48 |
68 |
5 |
50 |
70 |
7 |
52
|
| 35 |
80 |
17 |
28 |
73 |
10 |
33 |
78 |
15
|
| 26 |
44 |
62 |
19 |
37 |
55 |
24 |
42 |
60
|
| 71 |
8 |
53 |
64 |
1 |
46 |
69 |
6 |
51
|
|
Powyższe magiczne kwadraty rzędu 3 do 9 pochodzą z traktatu Yang Hui, w którym zasada Luo Shu jest wyraźnie widoczna. Kwadrat porządku 5 jest ograniczonym magicznym kwadratem, z centralnym kwadratem 3×3 utworzonym zgodnie z zasadą Luo Shu. Kwadrat rzędu 9 jest złożonym magicznym kwadratem, w którym dziewięć podkwadratów 3×3 jest również magicznych. Po Yang Hui, magiczne kwadraty często występują w chińskich matematyki takich jak Ding Yidong za Dayan suoyin ( ok. 1300 ), Cheng Dawei „s Suanfa tongzong (1593), Fang Zhongtong za Shuduyan (1661), który zawiera magiczne kręgi, kostki i kulki, Zhang Xinzhai zazu Chao ( ok. 1650 ), który opublikował pierwszy w Chinach magiczny kwadrat dziesiątego rzędu, a na końcu Binaishanfang ji Bao Qishou ( ok. 1880 ), który podał różne trójwymiarowe konfiguracje magiczne. Jednak pomimo tego, że jako pierwszy odkrył magiczne kwadraty i uzyskał przewagę o kilka stuleci, chiński rozwój magicznych kwadratów jest znacznie gorszy w porównaniu z rozwojem Indii, Bliskiego Wschodu czy Europy. Szczytowy punkt chińskiej matematyki, która zajmuje się magicznymi kwadratami, wydaje się być zawarty w pracy Yang Hui; ale nawet jako zbiór starszych metod, praca ta jest znacznie bardziej prymitywna, pozbawiona ogólnych metod konstruowania magicznych kwadratów dowolnej kolejności, w porównaniu z podobnym zbiorem napisanym w tym samym czasie przez bizantyjskiego uczonego Manuela Moschopoulosa . Jest to prawdopodobnie spowodowane zafascynowaniem chińskich uczonych zasadą Lo Shu, którą próbowali dostosować do rozwiązywania wyższych kwadratów; a po Yang Hui i upadku dynastii Yuan ich systematyczne oczyszczanie z obcych wpływów w chińskiej matematyce.
Japonia
Japonia i Chiny mają podobne tradycje matematyczne i wielokrotnie wpływały na siebie w historii magicznych kwadratów. Japoński zainteresowanie magicznych kwadratów rozpoczął się po rozpowszechnianie chińskim działa Yang Hui Suanfa Cheng Dawei Suanfa tongzong -w 17 wieku, aw rezultacie, prawie wszyscy wasans poświęca swój czas na jego badania.
W wydaniu Ketsugi-sho z 1660 r. Isomura Kittoku dał zarówno nieparzyste, jak i nawet uporządkowane obramowane magiczne kwadraty, a także magiczne kręgi; podczas gdy wydanie tej samej książki z 1684 r. zawierało dużą sekcję o magicznych kwadratach, co dowodzi, że miał ogólną metodę konstruowania obramowanych magicznych kwadratów. W Jinko-ki (1665) Muramatsu Kudayu Mosei pokazane są zarówno magiczne kwadraty, jak i magiczne kręgi. Największy kwadrat, który konstruuje Mosei, jest dziewiętnastego rzędu. Różne magiczne kwadraty i magiczne kręgi zostały również opublikowane przez Nozawę Teicho w Dokai-sho (1666), Sato Seiko w Kongenki (1666) i Hosino Sanenobu w Ko-ko-gen Sho (1673). Jednym z Seki Takakazu „s siedmiu książek ( Hojin Yensan ) (1683) poświęcona jest całkowicie magiczne kwadraty i okręgi. Jest to pierwsza japońska książka, która przedstawia ogólne podejście do magicznych kwadratów, w której wyraźnie opisano algorytmy konstruowania nieparzystych, pojedynczo parzystych i podwójnie parzystych magicznych kwadratów. W latach 1694 i 1695 Yueki Ando podał różne metody tworzenia magicznych kwadratów i wyświetlał kwadraty rzędu 3 do 30. Magiczna kostka czwartego rzędu została skonstruowana przez Yoshizane Tanaka (1651-1719) w Rakusho-kikan (1683). Badanie magicznych kwadratów kontynuowali uczniowie Seki, w szczególności Katahiro Takebe, którego kwadraty zostały pokazane w czwartym tomie Ichigen Kappo Shukei Irie, Yoshisuke Matsunaga w Hojin-Shin-jutsu , Yoshihiro Kurushima w Kyushi Iko, który na nowo odkrył metodę tworzą nieparzyste kwadraty podane przez Agryppę i Naonobu Ajimę . Tak więc na początku XVIII wieku matematycy japońscy dysponowali metodami konstruowania magicznych kwadratów o dowolnym porządku. Następnie próby wyliczenia magicznych kwadratów zapoczątkował Nushizumi Yamaji.
Indie

Magiczny kwadrat 3×3 w różnych orientacjach, tworzący nienormalny magiczny kwadrat 6×6, z niezidentyfikowanego indyjskiego manuskryptu z XIX wieku.
Magiczny kwadrat 3×3 po raz pierwszy pojawia się w Indiach w Gargasamhicie przez Gargę , który zaleca jego użycie do spacyfikowania dziewięciu planet ( navagraha ). Najstarsza wersja tego tekstu pochodzi z 100 n.e., ale fragment dotyczący planet nie mógł zostać napisany wcześniej niż 400 n.e. Pierwszy możliwy do datowania przypadek magicznego kwadratu 3×3 w Indiach występuje w tekście medycznym Siddhayog (ok. 900 ne) autorstwa Vrindy, który został przepisany kobietom podczas porodu w celu łatwego porodu.
Najstarszy możliwy do datowania magiczny kwadrat czwartego rzędu na świecie znajduje się w encyklopedycznym dziele napisanym przez Varahamihirę około 587 roku ne, zwanym Brhat Samhita . Magiczny kwadrat jest skonstruowany do tworzenia perfum z 4 substancji wybranych z 16 różnych substancji. Każda komórka kwadratu reprezentuje konkretny składnik, podczas gdy liczba w komórce reprezentuje proporcję powiązanego składnika, tak że mieszanina dowolnych czterech kombinacji składników wzdłuż kolumn, wierszy, przekątnych itd. daje całkowitą objętość mieszanki ma być 18. Chociaż książka jest głównie o wróżbiarstwie, magiczny kwadrat jest podany jako kwestia kombinatorycznego projektu i nie przypisuje się mu żadnych magicznych właściwości. Szczególne cechy tego magicznego kwadratu skomentował Bhattotpala (ok. 966 n.e.)
| 2 |
3 |
5 |
8
|
| 5 |
8 |
2 |
3
|
| 4 |
1 |
7 |
6
|
| 7 |
6 |
4 |
1
|
|
| 10 |
3 |
13 |
8
|
| 5 |
16 |
2 |
11
|
| 4 |
9 |
7 |
14
|
| 15 |
6 |
12 |
1
|
|
Podany powyżej kwadrat Varahamihiry ma sumę 18. Tutaj liczby od 1 do 8 pojawiają się dwukrotnie w kwadracie. Jest to magiczny kwadrat o przekątnej . Cztery różne magiczne kwadraty można uzyskać, dodając 8 do jednego z dwóch zestawów od 1 do 8. Sekwencja jest tak dobrana, że liczba 8 jest dodawana dokładnie dwa razy w każdym rzędzie, każdej kolumnie i każdej z głównych przekątnych. Jeden z możliwych magicznych kwadratów pokazany po prawej stronie. Ten magiczny kwadrat jest niezwykły, ponieważ jest to obrót o 90 stopni magicznego kwadratu, który pojawia się w XIII-wiecznym świecie islamskim jako jeden z najpopularniejszych magicznych kwadratów.
Budowa magicznego kwadratu czwartego rzędu jest szczegółowo opisana w dziele zatytułowanym Kaksaputa , skomponowanym przez alchemika Nagardżunę około X wieku n.e. Wszystkie kwadraty podane przez Nagardżunę to 4×4 magiczne kwadraty, a jeden z nich nazywa się od jego nazwiska Nagarjuniya . Nagardżuna podał metodę konstruowania magicznego kwadratu 4×4 przy użyciu podstawowego kwadratu szkieletu, otrzymując nieparzystą lub nawet magiczną sumę. Kwadrat Nagarjuniya jest podany poniżej i ma sumę 100.
| 30 |
16 |
18 |
36
|
| 10 |
44 |
22 |
24
|
| 32 |
14 |
20 |
34
|
| 28 |
26 |
40 |
6
|
|
| 7 |
1 |
4 |
6
|
| 2 |
8 |
5 |
3
|
| 5 |
3 |
2 |
8
|
| 4 |
6 |
7 |
1
|
|
Kwadrat Nagarjuniya to magiczny kwadrat o przekątnej . Kwadrat Nagarjuniya składa się z dwóch ciągów arytmetycznych, zaczynając od 6 i 16, każdy z ośmioma wyrazami, przy czym różnica między kolejnymi wyrazami wynosi 4. Gdy te dwa progreje zostaną zredukowane do normalnego ciągu od 1 do 8, otrzymujemy sąsiedni kwadrat .
Około XII wieku na ścianie świątyni Parshvanath w Khajuraho w Indiach wyryto magiczny kwadrat 4×4 . Kilka hymnów Jain uczy, jak tworzyć magiczne kwadraty, chociaż nie można ich datować.
O ile wiadomo, pierwsze systematyczne badania magicznych kwadratów w Indiach przeprowadził Thakkar Pheru , uczony dżinizmu, w swoim Ganitasara Kaumudi (ok. 1315). Ta praca zawiera mały rozdział o magicznych kwadratach, który składa się z dziewięciu wersetów. Tutaj podaje kwadrat czwartego rzędu i nawiązuje do jego przegrupowania; klasyfikuje magiczne kwadraty na trzy (nieparzyste, parzyste i nieparzyste) zgodnie z ich kolejnością; daje kwadrat rzędu sześć; i zaleca po jednej metodzie tworzenia parzystych i nieparzystych kwadratów. W przypadku kwadratów parzystych Pheru dzieli kwadrat na składowe kwadraty czwartego rzędu i umieszcza liczby w komórkach zgodnie ze wzorem standardowego kwadratu czwartego rzędu. W przypadku kwadratów nieparzystych Pheru podaje metodę za pomocą ruchu konia lub ruchu skoczka. Chociaż algorytmicznie różni się, daje ten sam kwadrat, co metoda De la Loubere'a.
Kolejną obszerną pracę nad magicznymi kwadratami podjął Narayana Pandit , który w czternastym rozdziale swojego Ganita Kaumudi (1356) podaje ogólne metody ich budowy wraz z zasadami rządzącymi takimi konstrukcjami. Składa się z 55 wersetów z zasadami i 17 wersetów z przykładami. Narayana podaje metodę konstruowania wszystkich wszechmagicznych kwadratów czwartego rzędu za pomocą ruchu skoczka; wylicza liczbę pandiagonalnych magicznych kwadratów rzędu czwartego, 384, w tym każdą wariację wykonaną przez obrót i odbicie; trzy ogólne metody dla kwadratów o dowolnym rzędzie i stałej sumie, gdy znany jest standardowy kwadrat tego samego rzędu; dwie metody, z których każda służy do konstruowania równych parzystych, dziwnie parzystych i nieparzystych kwadratów, gdy podana jest suma. Podczas gdy Narayana opisuje jedną starszą metodę dla każdego gatunku kwadratów, twierdzi, że metoda superpozycji dla kwadratów parzystych i nieparzystych oraz metoda wymiany kwadratów nieparzystych jest jego własnym wynalazkiem. Metoda superpozycji została później ponownie odkryta przez De la Hire w Europie. W ostatniej części rozważa inne figury, takie jak koła, prostokąty i sześciokąty, w których liczby mogą być ułożone tak, aby miały właściwości podobne do magicznych kwadratów. Poniżej znajdują się niektóre z magicznych kwadratów zbudowanych przez Narayana:
|
|
| 1 |
14 |
4 |
15
|
| 8 |
11 |
5 |
10
|
| 13 |
2 |
16 |
3
|
| 12 |
7 |
9 |
6
|
|
| 16 |
14 |
7 |
30 |
23
|
| 24 |
17 |
10 |
8 |
31
|
| 32 |
25 |
18 |
11 |
4
|
| 5 |
28 |
26 |
19 |
12
|
| 13 |
6 |
29 |
22 |
20
|
|
| 1 |
35 |
4 |
33 |
32 |
6
|
| 25 |
11 |
9 |
28 |
8 |
30
|
| 24 |
14 |
18 |
16 |
17 |
22
|
| 13 |
23 |
19 |
21 |
20 |
15
|
| 12 |
26 |
27 |
10 |
29 |
7
|
| 36 |
2 |
34 |
3 |
5 |
31
|
|
| 35 |
26 |
17 |
1 |
62 |
53 |
44
|
| 46 |
37 |
21 |
12 |
3 |
64 |
55
|
| 57 |
41 |
32 |
23 |
14 |
5 |
66
|
| 61 |
52 |
43 |
34 |
25 |
16 |
7
|
| 2 |
63 |
54 |
45 |
36 |
27 |
11
|
| 13 |
4 |
65 |
56 |
47 |
31 |
22
|
| 24 |
15 |
6 |
67 |
51 |
42 |
33
|
|
| 60 |
53 |
44 |
37 |
4 |
13 |
20 |
29
|
| 3 |
14 |
19 |
30 |
59 |
54 |
43 |
38
|
| 58 |
55 |
42 |
39 |
2 |
15 |
18 |
31
|
| 1 |
16 |
17 |
32 |
57 |
56 |
41 |
40
|
| 61 |
52 |
45 |
36 |
5 |
12 |
21 |
28
|
| 6 |
11 |
22 |
27 |
62 |
51 |
46 |
35
|
| 63 |
50 |
47 |
34 |
7 |
10 |
23 |
26
|
| 8 |
9 |
24 |
25 |
64 |
49 |
48 |
33
|
|
Kwadrat porządku 8 sam w sobie jest interesujący, ponieważ jest przykładem najdoskonalszego kwadratu magicznego. Nawiasem mówiąc, Narayana stwierdza, że celem studiowania magicznych kwadratów jest skonstruowanie jantry , zniszczenie ego złych matematyków i dla przyjemności dobrych matematyków. Temat magicznych kwadratów jest określany jako bhadraganita, a Narayana stwierdza, że po raz pierwszy nauczał ich ludzi bóg Śiwa .
Bliski Wschód, Afryka Północna, Iberia muzułmańska

Magiczny kwadrat 6×6 z
Księgi Cudów (z rękopisu z XVI wieku).
Chociaż wczesna historia magicznych kwadratów w Persji i Arabii nie jest znana, sugeruje się, że były one znane w czasach przedislamskich. Jest jednak jasne, że badanie magicznych kwadratów było powszechne w średniowiecznym islamie i uważano, że rozpoczęło się ono po wprowadzeniu szachów do tego regionu. Pierwsze dające się datować pojawienie się kwadratu magicznego rzędu 3 pojawia się u Jabira ibn Hayyāna (fl. ok. 721 – ok. 815) Kitab al-mawazin al-Saghir (Mała księga sald), gdzie magiczny kwadrat i pokrewny mu numerologia związana jest z alchemią. Chociaż wiadomo, że traktaty o magicznych kwadratach zostały napisane w IX wieku, najwcześniejsze zachowane traktaty, jakie mamy, pochodzą z X wieku: jeden autorstwa Abu'l-Wafy al-Buzjaniego ( ok. 998 ), a drugi Ali b. Ahmad al-Antaki ( ok. 987 ). Te wczesne traktaty były czysto matematyczne, a arabskie oznaczenie magicznych kwadratów to wafq al-a'dad , co tłumaczy się jako harmonijne rozmieszczenie liczb . Pod koniec X wieku z dwóch traktatów Buzjaniego i Antakiego jasno wynika, że matematycy Bliskiego Wschodu zrozumieli, jak konstruować obramowane kwadraty dowolnego rzędu, a także proste magiczne kwadraty małych rzędów ( n ≤ 6), których używano do tworzyć złożone magiczne kwadraty. Okaz magicznych kwadratów rzędu 3 do 9, opracowanych przez matematyków z Bliskiego Wschodu, pojawia się w encyklopedii z Bagdadu w. 983 , Rasa'il Ikhwan al-Safa ( Encyklopedia Braci Czystości ). Kwadraty rzędu 3 do 7 z Rasa'il są podane poniżej:
|
|
| 4 |
14 |
15 |
1
|
| 9 |
7 |
6 |
12
|
| 5 |
11 |
10 |
8
|
| 16 |
2 |
3 |
13
|
|
| 21 |
3 |
4 |
12 |
25
|
| 15 |
17 |
6 |
19 |
8
|
| 10 |
24 |
13 |
2 |
16
|
| 18 |
7 |
20 |
9 |
11
|
| 1 |
14 |
22 |
23 |
5
|
|
| 11 |
22 |
32 |
5 |
23 |
18
|
| 25 |
16 |
7 |
30 |
13 |
20
|
| 27 |
6 |
35 |
36 |
4 |
3
|
| 10 |
31 |
1 |
2 |
33 |
34
|
| 14 |
19 |
8 |
29 |
26 |
15
|
| 24 |
17 |
28 |
9 |
12 |
21
|
|
| 47 |
11 |
8 |
9 |
6 |
45 |
49
|
| 4 |
37 |
20 |
17 |
16 |
35 |
46
|
| 2 |
18 |
26 |
21 |
28 |
32 |
48
|
| 43 |
19 |
27 |
25 |
23 |
31 |
7
|
| 38 |
36 |
22 |
29 |
24 |
14 |
12
|
| 40 |
15 |
30 |
33 |
34 |
13 |
10
|
| 1 |
39 |
42 |
41 |
44 |
5 |
3
|
|
W XI wieku odkryto kilka sposobów na konstruowanie prostych magicznych kwadratów dla nieparzystych i parzystych zamówień; trudniejszy przypadek parzysto-nieparzystych ( n = 4k + 2 ) rozwiązał Ibn al-Haytham z k parzystym (ok. 1040) i całkowicie na początku XII wieku, jeśli nie już w drugiej połowie 11 wiek. Mniej więcej w tym samym czasie powstawały kwadraty pandiagonalne. W XI i XII wieku liczne były traktaty o magicznych placach. Te późniejsze zmiany były zwykle ulepszeniami lub uproszczeniami istniejących metod. Od XIII wieku na podgrodziach magiczne kwadraty coraz częściej były wykorzystywane do celów okultystycznych. Jednak wiele z tych późniejszych tekstów napisanych dla celów okultystycznych przedstawia jedynie pewne magiczne kwadraty i wspomina o ich atrybutach, bez opisywania ich zasady konstrukcji, a tylko niektórzy autorzy utrzymują przy życiu ogólną teorię. Jednym z takich okultystów był algierski Ahmad al-Buni (ok. 1225), który podał ogólne metody tworzenia obramowanych magicznych kwadratów; kilka innych to XVII-wieczny egipski Shabramallisi i XVIII-wieczny nigeryjski al-Kishnawi.
Magiczny kwadrat trzeciego rzędu był opisywany jako urok rozrodczy od pierwszych literackich wystąpień w alchemicznych dziełach Jābira ibn Hayyāna (fl. ok. 721 – ok. 815) i al-Ghazāli (1058–1111) i był zachowane w tradycji tablic planetarnych. Najwcześniejsze wystąpienie związku siedmiu magicznych kwadratów z zaletami siedmiu ciał niebieskich pojawia się u andaluzyjskiego uczonego Ibn Zarkali (znanego w Europie jako Azarquiel) (1029–1087) Kitāb tadbīrāt al-kawākib ( Księga o wpływach Planety ). Sto lat później algierski uczony Ahmad al-Buni przypisał magicznym kwadratom mistyczne właściwości w swojej bardzo wpływowej książce Shams al-Ma'arif ( Księga Słońca Gnozy i Subtelności Podniesionych Rzeczy ), która również opisuje ich budowę. Ta tradycja o serii magicznych kwadratów od trzeciego do dziewiątego, które są związane z siedmioma planetami, przetrwała w wersjach greckiej, arabskiej i łacińskiej. Istnieją również odniesienia do używania magicznych kwadratów w obliczeniach astrologicznych, praktyki, która wydaje się pochodzić od Arabów.
Europa Łacińska

Ta strona z
Atanazy Kircher „s
Edypa aegiptiacus (1653) należy do traktatu o magicznych kwadratów i pokazuje
Sigillum IOVIS związanych z Jowiszem
W przeciwieństwie do Persji i Arabii mamy lepszą dokumentację tego, w jaki sposób magiczne kwadraty zostały przeniesione do Europy. Około 1315 r., pod wpływem źródeł arabskich, grecki bizantyjski uczony Manuel Moschopoulos napisał traktat matematyczny na temat magicznych kwadratów, pomijając mistycyzm swoich bliskowschodnich poprzedników, gdzie podał dwie metody dla kwadratów nieparzystych i dwie metody dla kwadratów równych. . Moschopoulos był zasadniczo nieznany w Europie Łacińskiej aż do końca XVII wieku, kiedy Philippe de la Hire ponownie odkrył swój traktat w Bibliotece Królewskiej w Paryżu. Nie był jednak pierwszym Europejczykiem, który pisał na magicznych kwadratach; a magiczne kwadraty zostały rozpowszechnione w całej Europie przez Hiszpanię i Włochy jako przedmioty okultystyczne. Wczesne traktaty okultystyczne, które przedstawiały kwadraty, nie opisywały, jak zostały zbudowane. Tak więc cała teoria musiała zostać odkryta na nowo.
Magiczne kwadraty pojawiły się po raz pierwszy w Europie w Kitāb tadbīrāt al-kawākib ( Księdze o wpływach planet ), napisanej przez Ibn Zarkali z Toledo w Al-Andalus, jako kwadraty planetarne w XI wieku. Magiczny kwadrat trzech został omówiony w sposób numerologiczny na początku XII wieku przez żydowskiego uczonego Abrahama ibn Ezra z Toledo, który miał wpływ na późniejszych kabalistów. Dzieło Ibn Zarkali zostało przetłumaczone jako Libro de Astromagia w latach 80. XIX wieku, za sprawą Alfonsa X z Kastylii. W tekście Alfonsine'a magiczne kwadraty różnych porządków są przypisane do odpowiednich planet, tak jak w literaturze islamskiej; niestety, ze wszystkich omawianych kwadratów, magiczny kwadrat Marsa rzędu piątego jest jedynym kwadratem wystawionym w manuskrypcie.
Magiczne kwadraty pojawiły się ponownie we Florencji we Włoszech w XIV wieku. Kwadrat 6×6 i 9×9 są wystawione w rękopisie Trattato d'Abbaco (Traktatu Abacus) Paolo Dagomari . Warto zauważyć, że Paolo Dagomari, podobnie jak po nim Pacioli, odnosi się do kwadratów jako użytecznej podstawy do wymyślania matematycznych pytań i gier i nie wspomina o żadnym magicznym użyciu. Nawiasem mówiąc, odnosi się on również do nich jako odpowiednio do kwadratów Słońca i Księżyca i wspomina, że wchodzą one w obliczenia astrologiczne, które nie są lepiej określone. Jak już powiedziano, ten sam punkt widzenia wydaje się motywować florentyńczyka Luca Pacioli , który pod koniec XV wieku opisuje kwadraty o wymiarach 3×3 do 9×9 w swojej pracy De Viribus Quantitatis .
Europa po XV wieku

Strona z książki Simon de la Loubère
Du Royaume de Siam (1691) przedstawiająca indyjską metodę konstruowania dziwnego magicznego kwadratu.
Kwadraty planetarne rozprzestrzeniły się w północnej Europie pod koniec XV wieku. Na przykład krakowski rękopis Picatrixa z Polski zawiera magiczne kwadraty rzędu 3 do 9. Ten sam układ kwadratów, co w krakowskim rękopisie, pojawia się później w pismach Paracelsusa w Archidoxa Magica (1567), choć w mocno zniekształconej formie. W 1514 roku Albrecht Dürer uwiecznił kwadrat 4×4 w swojej słynnej rycinie Melencolia I . Współczesny Paracelsusowi Heinrich Cornelius Agrippa von Nettesheim opublikował w 1531 roku swoją słynną trzytomową książkę De occulta philosophia, w której poświęcił rozdział 22 księgi II pokazanym poniżej kwadratom planetarnym. Ten sam zestaw kwadratów podanych przez Agrippa ponownie w 1539 roku w Practica Arithmetice przez Girolamo Cardano , gdzie wyjaśnia budowę nieparzystych zamówionych kwadratów z wykorzystaniem metody „diament”, która została później powielane przez Bachet. Tradycję kwadratów planetarnych kontynuował w XVII wieku Athanasius Kircher w Oedipi Aegyptici (1653). W Niemczech traktaty matematyczne dotyczące magicznych kwadratów zostały napisane w 1544 r. przez Michaela Stifela w Arithmetica Integra , który na nowo odkrył kwadraty obramowane, oraz Adama Riese , który na nowo odkrył metodę numeracji ciągłej, aby skonstruować nieparzyste uporządkowane kwadraty opublikowane przez Agryppę. Jednak ze względu na przewroty religijne tamtych czasów prace te były nieznane reszcie Europy.
|
|
Jowisz =34
| 4 |
14 |
15 |
1
|
| 9 |
7 |
6 |
12
|
| 5 |
11 |
10 |
8
|
| 16 |
2 |
3 |
13
|
|
Mars =65
| 11 |
24 |
7 |
20 |
3
|
| 4 |
12 |
25 |
8 |
16
|
| 17 |
5 |
13 |
21 |
9
|
| 10 |
18 |
1 |
14 |
22
|
| 23 |
6 |
19 |
2 |
15
|
|
Sol =111
| 6 |
32 |
3 |
34 |
35 |
1
|
| 7 |
11 |
27 |
28 |
8 |
30
|
| 19 |
14 |
16 |
15 |
23 |
24
|
| 18 |
20 |
22 |
21 |
17 |
13
|
| 25 |
29 |
10 |
9 |
26 |
12
|
| 36 |
5 |
33 |
4 |
2 |
31
|
|
Wenus =175
| 22 |
47 |
16 |
41 |
10 |
35 |
4
|
| 5 |
23 |
48 |
17 |
42 |
11 |
29
|
| 30 |
6 |
24 |
49 |
18 |
36 |
12
|
| 13 |
31 |
7 |
25 |
43 |
19 |
37
|
| 38 |
14 |
32 |
1 |
26 |
44 |
20
|
| 21 |
39 |
8 |
33 |
2 |
27 |
45
|
| 46 |
15 |
40 |
9 |
34 |
3 |
28
|
|
Merkury =260
| 8 |
58 |
59 |
5 |
4 |
62 |
63 |
1
|
| 49 |
15 |
14 |
52 |
53 |
11 |
10 |
56
|
| 41 |
23 |
22 |
44 |
45 |
19 |
18 |
48
|
| 32 |
34 |
35 |
29 |
28 |
38 |
39 |
25
|
| 40 |
26 |
27 |
37 |
36 |
30 |
31 |
33
|
| 17 |
47 |
46 |
20 |
21 |
43 |
42 |
24
|
| 9 |
55 |
54 |
12 |
13 |
51 |
50 |
16
|
| 64 |
2 |
3 |
61 |
60 |
6 |
7 |
57
|
|
Księżyc = 369
| 37 |
78 |
29 |
70 |
21 |
62 |
13 |
54 |
5
|
| 6 |
38 |
79 |
30 |
71 |
22 |
63 |
14 |
46
|
| 47 |
7 |
39 |
80 |
31 |
72 |
23 |
55 |
15
|
| 16 |
48 |
8 |
40 |
81 |
32 |
64 |
24 |
56
|
| 57 |
17 |
49 |
9 |
41 |
73 |
33 |
65 |
25
|
| 26 |
58 |
18 |
50 |
1 |
42 |
74 |
34 |
66
|
| 67 |
27 |
59 |
10 |
51 |
2 |
43 |
75 |
35
|
| 36 |
68 |
19 |
60 |
11 |
52 |
3 |
44 |
76
|
| 77 |
28 |
69 |
20 |
61 |
12 |
53 |
4 |
45
|
|
W 1624 roku we Francji Claude Gaspard Bachet opisał w swojej książce „ Problèmes Plaisants ” „metodę diamentową” konstruowania dziwnie uporządkowanych kwadratów Agryppy . W 1640 roku Bernard Frenicle de Bessy i Pierre Fermat wymienili listy na magicznych kwadratach i sześcianach, aw jednym z listów Fermat chwalił się, że był w stanie skonstruować 1 004 144 995 344 magicznych kwadratów rzędu 8 swoją metodą. Antoine Arnauld w swoim Nouveaux éléments de géométrie (1667) podał wczesne relacje o budowie graniczących kwadratów . W dwóch traktatach Des quarrez ou tables magiques i Table générale des quarrez magiques de quatre de côté , opublikowanych pośmiertnie w 1693 roku, dwadzieścia lat po jego śmierci, Bernard Frenicle de Bessy wykazał, że istnieje dokładnie 880 odrębnych magicznych kwadratów czwartego rzędu. Frenicle podał metody konstruowania magicznych kwadratów o dowolnym nieparzystym i parzystym porządku, gdzie parzyste uporządkowane kwadraty były konstruowane przy użyciu obramowań. Pokazał również, że zamieniające się rzędy i kolumny magicznego kwadratu tworzyły nowe magiczne kwadraty. W 1691 r. Simon de la Loubère opisał indyjską ciągłą metodę konstruowania dziwnie uporządkowanych magicznych kwadratów w swojej książce Du Royaume de Siam , której nauczył się wracając z misji dyplomatycznej do Syjamu, co było szybsze niż metoda Bachet. Próbując wyjaśnić jego działanie, de la Loubere użył liczb pierwotnych i pierwiastków i na nowo odkrył metodę dodawania dwóch wstępnych kwadratów. Metoda ta była dalej badana przez Abbe Poignarda w Traité des quarrés sublimes (1704), przez Philippe'a de La Hire w Mémoires de l'Académie des Sciences dla Akademii Królewskiej (1705) oraz przez Josepha Sauveura w Construction des quarrés magiques (1710). . Koncentryczne obramowane kwadraty były również badane przez De la Hire w 1705 roku, podczas gdy Sauveur wprowadził magiczne sześciany i kwadraty z literami, które zostały później podjęte przez Eulera w 1776 roku, któremu często przypisuje się ich opracowanie. W 1750 d'Ons-le-Bray na nowo odkrył metodę konstruowania podwójnie równych i pojedynczo równych kwadratów przy użyciu techniki obramowania; podczas gdy w 1767 Benjamin Franklin opublikował półmagiczny kwadrat, który miał właściwości tytułowego kwadratu Franklina. Do tego czasu wcześniejszy mistycyzm związany z magicznymi kwadratami całkowicie zniknął, a przedmiot był traktowany jako część matematyki rekreacyjnej.
W XIX wieku Bernard Violle przedstawił kompleksową analizę magicznych kwadratów w swoich trzech tomach Traité complet des carrés magiques (1837-1838), w których opisano również magiczne sześciany, równoległoboki, równoległościany i koła. Kwadraty pandiagonal były szeroko badane przez Andrew Hollingwortha Frosta, który poznał je w mieście Nasik w Indiach (stąd nazywając je kwadratami Nasik) w serii artykułów: On the knight's path (1877), On the General Properties of Nasik Squares (1878), O ogólnych właściwościach sześcianów Nasik (1878), O budowie Placów Nasika dowolnej kolejności (1896). Pokazał, że nie można mieć normalnego, pojedynczego, nawet pandiagonalnego kwadratu magicznego. Frederick AP Barnard skonstruował inkrustowane magiczne kwadraty i inne trójwymiarowe figury magiczne, takie jak magiczne kule i magiczne cylindry w Teorii magicznych kwadratów i magicznych kostek (1888). W 1897 roku Emroy McClintock opublikował O najdoskonalszej formie magicznych kwadratów , ukuł słowa pandiagonal kwadrat i najdoskonalszy kwadrat , które wcześniej określano mianem doskonałego, diabolicznego lub Nasika.
Niektóre słynne magiczne kwadraty

Lo Shu z „Zjawisk astronomicznych” (
Tien Yuan Fa Wei ). Opracowane przez Bao Yunlonga w XIII wieku, opublikowane w okresie
dynastii Ming w latach 1457-1463.
Magiczny kwadrat Luo Shu
Legendy pochodzące już z 650 roku p.n.e. opowiadają historię Lo Shu (洛書) lub „zwoju rzeki Lo”. Według legendy w starożytnych Chinach była kiedyś wielka powódź. Podczas gdy wielki król Yu próbował skierować wodę do morza, wyłonił się z niego żółw z dziwnym wzorem na skorupie: siatka 3×3, w której okrągłe kropki liczb były ułożone w taki sposób, że suma liczb w każdy rząd, kolumna i przekątna były takie same: 15. Według legendy odtąd ludzie mogli w pewien sposób wykorzystać ten wzór do kontrolowania rzeki i ochrony przed powodziami. Luoshu , jak kwadrat magiczny na skorupy żółwia nazywa, jest unikalny normalny magiczny kwadrat z rzędu trzy, w których 1 jest na dole i 2 znajduje się w prawym górnym rogu. Każdy normalny magiczny kwadrat rzędu trzeciego jest otrzymywany z Lo Shu przez rotację lub odbicie.
Magiczny plac w świątyni Parshavnath
Na ścianie świątyni Parshvanath w Khajuraho w Indiach znajduje się dobrze znany XII-wieczny normalny magiczny kwadrat 4×4 .
| 7 |
12 |
1 |
14
|
| 2 |
13 |
8 |
11
|
| 16 |
3 |
10 |
5
|
| 9 |
6 |
15 |
4
|
Jest to znane jako Chautisa Yantra, ponieważ jego magiczna suma wynosi 34. Jest to jeden z trzech pandiagonalnych magicznych kwadratów 4×4 i jest również przykładem najdoskonalszego magicznego kwadratu . Badanie tego kwadratu doprowadziło do uznania kwadratów pandiagonalnych przez europejskich matematyków pod koniec XIX wieku. Kwadraty pandiagonalne były określane jako kwadraty Nasik lub kwadraty Jain w starszej literaturze angielskiej.
Magiczny kwadrat Albrechta Dürera
Porządek czterech normalnych magicznych kwadratów uwieczniony przez Albrechta Dürera w jego rycinie Melencolia I z 1514 roku , o którym mowa powyżej, jest uważany za pierwszy w sztuce europejskiej. Kwadrat związany z Jowiszem jawi się jako talizman służący do odpędzania melancholii. Jest bardzo podobny do placu Yang Hui , który powstał w Chinach około 250 lat przed czasami Dürera. Jak w przypadku każdego rzędu 4 normalne magiczne kwadraty, magiczna suma wynosi 34. Ale w kwadracie Durera ta suma znajduje się również w każdym z kwadrantów, w środkowych czterech kwadratach i w narożnych kwadratach (również ponieważ cztery zawierały siatki 3×3). Sumę tę można również znaleźć w czterech zewnętrznych liczbach zgodnie z ruchem wskazówek zegara od rogów (3+8+14+9) i podobnie w czterech przeciwnych do ruchu wskazówek zegara (położenie czterech hetmanów w dwóch rozwiązaniach łamigłówki 4 hetmanów ). zestawy czterech liczb symetrycznych (2+8+9+15 i 3+5+12+14), suma środkowych dwóch wpisów dwóch zewnętrznych kolumn i wierszy (5+9+8+12 i 3+2+ 15+14) oraz w czterech kwartetach w kształcie latawca lub krzyża (3+5+11+15, 2+10+8+14, 3+9+7+15 i 2+6+12+14). Dwie cyfry pośrodku dolnego rzędu podają datę ryciny: 1514. Cyfry 1 i 4 po obu stronach daty odpowiadają odpowiednio literom „A” i „D”, które są inicjałami artysty .
| 16 |
3 |
2 |
13
|
| 5 |
10 |
11 |
8
|
| 9 |
6 |
7 |
12
|
| 4 |
15 |
14 |
1
|
Magiczny kwadrat Dürera można również rozszerzyć do magicznej kostki.
Magiczny plac Sagrada Família

Magiczny plac na fasadzie kościoła Sagrada Família
Fasada pasyjna kościoła Sagrada Família w Barcelonie , zaprojektowana przez Antoniego Gaudiego i zaprojektowana przez rzeźbiarza Josepa Subirachsa , przedstawia trywialny magiczny kwadrat rzędu 4: Magiczna stała kwadratu to 33, wiek Jezusa w czasie Męki Pańskiej . Strukturalnie jest bardzo podobny do magicznego kwadratu Melancholii, ale liczba czterech komórek została zmniejszona o 1.
| 1 |
14 |
14 |
4
|
| 11 |
7 |
6 |
9
|
| 8 |
10 |
10 |
5
|
| 13 |
2 |
3 |
15
|
Trywialne kwadraty, takie jak ten, nie są na ogół interesujące matematycznie i mają jedynie znaczenie historyczne. Lee Sallows zwrócił uwagę, że z powodu nieznajomości teorii kwadratów magicznych Subirachsa, słynny rzeźbiarz popełnił niepotrzebny błąd i potwierdza to twierdzenie, podając kilka przykładów nietrywialnych magicznych kwadratów 4×4 pokazujących pożądaną stałą magiczną 33.
Podobnie jak magiczny kwadrat Dürera, magiczny kwadrat Sagrady Familii można również rozszerzyć do magicznej kostki.
Plac Parkera
Parker plac , nazwany po matematyk wypoczynkowe Matt Parker , jest próbą stworzenia 3 x 3 magiczny kwadrat kwadratów - ceniona nierozwiązany problem, ponieważ Eulera . Kwadrat Parkera jest trywialnym półmagicznym kwadratem, ponieważ używa niektórych liczb więcej niż raz, a przekątna 23 2 + 37 2 + 47 2 sumuje się do4107 , nie3051 jak dla wszystkich innych rzędów, kolumn lub przekątnych. Parker Square stał się „maskotką dla ludzi, którzy próbują, ale w końcu im się nie udaje”. Jest to również metafora czegoś, co jest prawie słuszne, ale trochę nie tak.
| 29 2
|
1 2
|
47 2
|
| 41 2
|
37 2
|
1 2
|
| 23 2
|
41 2
|
29 2
|
Właściwości magicznych kwadratów
Magiczna stała
Stałą będącą sumą dowolnego wiersza, kolumny lub przekątnej nazywa się magiczną stałą lub magiczną sumą M. Każdy normalny magiczny kwadrat ma stałą zależną od rzędu n , obliczoną za pomocą wzoru . Można to wykazać, zauważając, że suma wynosi . Ponieważ suma każdego wiersza to , suma wierszy to , co po podzieleniu przez rząd n daje magiczną stałą. Dla normalnych magicznych kwadratów rzędów n = 3, 4, 5, 6, 7 i 8, magiczne stałe wynoszą odpowiednio: 15, 34, 65, 111, 175 i 260 (sekwencja A006003 w OEIS ).






Magiczny kwadrat rzędu 1 jest trywialny
Magiczny kwadrat 1×1, z tylko jedną komórką zawierającą liczbę 1, nazywany jest trywialnym , ponieważ zazwyczaj nie jest brany pod uwagę przy omawianiu magicznych kwadratów; ale z definicji jest to magiczny kwadrat, jeśli uznamy pojedynczą komórkę za kwadrat rzędu pierwszego.
Magiczny kwadrat rzędu 2 nie może być skonstruowany
Można skonstruować zwykłe magiczne kwadraty wszystkich rozmiarów z wyjątkiem 2×2 (to znaczy, gdzie kolejność n = 2).
Środek masy
Jeśli myślimy o liczbach w magicznym kwadracie jako o masach znajdujących się w różnych komórkach, to środek masy magicznego kwadratu pokrywa się z jego geometrycznym środkiem.
Moment bezwładności
Moment bezwładności magicznego kwadratu został zdefiniowany jako suma nad wszystkimi komórkami liczby w czasach komórkowych kwadrat odległości od środka komórki na środku placu; tutaj jednostką miary jest szerokość jednej komórki. (Tak więc na przykład komórka narożna kwadratu 3×3 ma odległość od komórki nienarożnej na krawędzi ma odległość 1, a komórka środkowa ma odległość 0.) Wtedy wszystkie magiczne kwadraty danego rzędu mają ten sam moment bezwładności jak każdy inny. Dla przypadku rzędu 3 moment bezwładności wynosi zawsze 60, natomiast dla przypadku rzędu 4 moment bezwładności wynosi zawsze 340. Ogólnie dla przypadku n × n moment bezwładności wynosi

Rozkład Birkhoffa–von Neumanna
Dzieląc każdą liczbę magicznego kwadratu przez magiczną stałą otrzymamy podwójnie stochastyczną macierz , której sumy wierszy i sumy kolumn są równe jedności. Jednak w przeciwieństwie do macierzy podwójnie stochastycznej, sumy diagonalne takich macierzy będą również równe jedności. Tak więc takie macierze stanowią podzbiór macierzy podwójnie stochastycznych. Twierdzenie Birkhoffa-von Neumanna stwierdza, że dla każdej podwójnie stochastycznej macierzy , istnieją liczby rzeczywiste , gdzie i macierze permutacji takie, że





Ta reprezentacja może ogólnie nie być unikalna. Jednak według twierdzenia Marcusa-Ree'a w każdym rozkładzie nie musi być więcej niż wyrazów. Oczywiście ta dekompozycja przenosi się również na magiczne kwadraty, ponieważ możemy odzyskać magiczny kwadrat z podwójnie stochastycznej macierzy, mnożąc go przez magiczną stałą.

Klasyfikacja magicznych kwadratów

Diagram Eulera wymagań niektórych typów magicznych kwadratów 4×4. Komórki tego samego koloru sumują się do stałej magicznej. * W najdoskonalszych magicznych kwadratach 4×4 dowolne 2 komórki oddalone od siebie o 2 komórki po przekątnej (w tym zawijanie) sumują się do połowy stałej magicznej, stąd dowolne 2 takie pary również sumują się do stałej magicznej.
Chociaż klasyfikację magicznych kwadratów można przeprowadzić na wiele sposobów, poniżej podano kilka przydatnych kategorii. N x n macierz kwadratową liczby całkowite 1, 2, ..., n 2 nazywa się:
-
Półmagiczny kwadrat, gdy suma jego wierszy i kolumn daje magiczną stałą.
-
Prosty magiczny kwadrat, gdy suma jego wierszy, kolumn i dwóch przekątnych daje stałą magiczną i nic więcej. Są one również znane jako zwykłe magiczne kwadraty lub normalne magiczne kwadraty .
-
Samouzupełniający się magiczny kwadrat, gdy jest magicznym kwadratem, który po uzupełnieniu (tj. każdej liczbie odejmowanej od n 2 + 1) da obróconą lub odbitą wersję oryginalnego magicznego kwadratu.
-
Magiczny kwadrat asocjacyjny, gdy jest to magiczny kwadrat z dodatkową właściwością, że każda liczba dodana do liczby równoodległej, w linii prostej od środka, daje n 2 + 1. Nazywa się je również symetrycznymi magicznymi kwadratami . Powiązane magiczne kwadraty nie istnieją dla kwadratów o pojedynczej, równej kolejności. Wszystkie powiązane magiczne kwadraty są również samouzupełniającymi się magicznymi kwadratami.
-
Magiczny kwadrat pandiagonalny, gdy jest to kwadrat magiczny z dodatkową właściwością, że złamane przekątne sumują się do stałej magicznej. Są one również nazywane panmagic kwadraty , idealne kwadraty , diaboliczni kwadraty , Jain kwadraty lub Nasik kwadraty . Kwadraty panmagiczne nie istnieją dla pojedynczych, nawet rozkazów. Jednak pojedynczo nawet nienormalne kwadraty mogą być panmagiczne.
-
Ultra magiczny kwadrat, gdy jest zarówno asocjacyjnym, jak i pandiagonalnym kwadratem magicznym. Ultra magiczny kwadrat istnieje tylko dla zamówień n ≥ 5.
-
Obramowany magiczny kwadrat, gdy jest magicznym kwadratem i pozostaje magiczny, gdy rzędy i kolumny na zewnętrznej krawędzi zostaną usunięte. Nazywa się je również koncentrycznymi obramowanymi magicznymi kwadratami, jeśli usunięcie obramowania kwadratu daje kolejny mniejszy obramowany magiczny kwadrat. Obramowany magiczny kwadrat nie istnieje dla zamówienia 4.
-
Złożony magiczny kwadrat, gdy jest to magiczny kwadrat utworzony przez „mnożenie” (w pewnym sensie) mniejszych magicznych kwadratów, tak że rząd złożonego magicznego kwadratu jest wielokrotnością rzędu mniejszych kwadratów. Takie kwadraty można zwykle podzielić na mniejsze, nienakładające się magiczne podkwadraty.
-
Inkrustowany magiczny kwadrat, gdy jest to magiczny kwadrat, w którym osadzony jest magiczny podkwadrat, niezależnie od techniki budowy. Osadzone magiczne podkwadraty same w sobie są określane jako inkrustacje .
-
Najdoskonalszy magiczny kwadrat, gdy jest to kwadrat magiczny o dwóch dalszych właściwościach (i) każdy podkwadrat 2×2 dodaje się do 1/ k stałej magicznej, gdzie n = 4 k , oraz (ii) wszystkie pary liczb całkowitych odległe n / 2 wzdłuż dowolnej przekątnej (większej lub łamanej) są komplementarne (tzn. sumują się do n 2 + 1). Pierwsza właściwość jest określana jako zwartość , podczas gdy druga właściwość jest określana jako zupełność . Najdoskonalsze magiczne kwadraty istnieją tylko dla kwadratów podwójnie równych. Wszystkie kwadraty pandiagonalne rzędu 4 są również najdoskonalsze.
-
Magiczny kwadrat Franklina, gdy jest podwójnie parzystym kwadratem magicznym z trzema dalszymi właściwościami (i) każda wygięta przekątna dodaje do stałej magicznej, (ii) każde pół rzędu i pół kolumny zaczynające się od zewnętrznej krawędzi dodaje do połowy stałej magicznej, oraz ( iii) kwadrat jest zwarty .
-
Kwadrat multimagiczny, gdy jest magicznym kwadratem, który pozostaje magiczny, nawet jeśli wszystkie jego liczby zostaną zastąpione ich k-tą potęgą dla 1 ≤ k ≤ P . Znane są również jako kwadraty P-multimagiczne lub szatańskie . Są one również określane jako bimagiczne kwadraty , trimagiczne kwadraty , tetramagiczne kwadraty , pentamagiczne kwadraty, gdy wartość P wynosi odpowiednio 2, 3, 4 i 5.
Wyliczanie magicznych kwadratów
Nierozwiązany problem w matematyce :
Ile magiczne kwadraty, a ilu magia tori z rzędu n , są tam ?

- Kwadraty niskiego rzędu
Jest tylko jeden (trywialny) magiczny kwadrat rzędu 1 i nie ma magicznego kwadratu rzędu 2. Jak wspomniano powyżej, zbiór normalnych kwadratów rzędu trzeciego stanowi pojedynczą klasę równoważności – wszystkie są równoważne kwadratowi Lo Shu. Tak więc istnieje tylko jeden normalny magiczny kwadrat rzędu 3.
Liczba różnych n × n magicznych kwadratów dla n od 1 do 5, nie licząc obrotów i odbić, wynosi:
- 1, 0, 1, 880, 275305224. (sekwencja A006052 w OEIS )
Liczbę dla n = 6 oszacowano na (1,7745 ± 0,0016) × 10 19 .
- Magiczne tory
W odniesieniu do powyższej sekwencji nowa klasyfikacja wylicza magiczne tori, które wyświetlają te magiczne kwadraty. Liczba magicznych tori rzędu n od 1 do 5 to:
- 1, 0, 1, 255, 251449712 (sekwencja A270876 w OEIS ).
- Kwadraty wyższego rzędu i tori
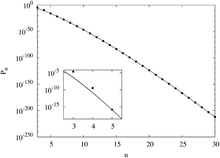
Wykres półlogarytmiczny Pn, prawdopodobieństwo magicznych kwadratów wymiaru n
Liczba odrębnych normalnych magicznych kwadratów gwałtownie wzrasta dla wyższych rzędów.
880 magicznych kwadratów rzędu 4 jest wyświetlanych na 255 magicznych tori rzędu 4, a 275 305 224 kwadraty rzędu 5 jest wyświetlanych na 251 449 712 magicznych tori rzędu 5. Liczba magicznych tori i odrębnych normalnych kwadratów nie jest jeszcze znana dla żadnego wyższego rzędu .
Algorytmy mają tendencję do generowania magicznych kwadratów tylko określonego typu lub klasyfikacji, co sprawia, że liczenie wszystkich możliwych magicznych kwadratów jest dość trudne. Tradycyjne metody liczenia okazały się nieskuteczne, zastosowano analizę statystyczną metodą Monte Carlo . Podstawową zasadą stosowaną do magicznych kwadratów jest losowe generowanie n × n macierzy elementów od 1 do n 2 i sprawdzenie, czy wynik jest magicznym kwadratem. Prawdopodobieństwo, że losowo wygenerowana macierz liczb jest magicznym kwadratem, jest następnie wykorzystywane do przybliżenia liczby magicznych kwadratów.
Bardziej skomplikowane wersje metody Monte Carlo, takie jak wymiana Monte Carlo i cofanie Monte Carlo, dały jeszcze dokładniejsze szacunki. Korzystając z tych metod wykazano, że prawdopodobieństwo magicznych kwadratów szybko spada wraz ze wzrostem n. Używając funkcji dopasowania, daj krzywe widoczne po prawej stronie.
Transformacje, które zachowują magiczną właściwość
Dla każdego magicznego kwadratu
- Magiczny kwadrat pozostaje magiczny, gdy jego liczby są pomnożone przez dowolną stałą.
- Magiczny kwadrat pozostaje magiczny, gdy do jego liczb jest dodawana lub odejmowana stała, albo gdy jego liczby są odejmowane od stałej. W szczególności, jeśli każdy element w normalnym magicznym kwadracie jest odejmowany od n 2 + 1, otrzymujemy uzupełnienie oryginalnego kwadratu. W poniższym przykładzie elementy kwadratu 4×4 po lewej stronie odejmuje się od 17, aby otrzymać dopełnienie kwadratu po prawej stronie.
| 10 |
3 |
13 |
8
|
| 5 |
16 |
2 |
11
|
| 4 |
9 |
7 |
14
|
| 15 |
6 |
12 |
1
|
|
| 7 |
14 |
4 |
9
|
| 12 |
1 |
15 |
6
|
| 13 |
8 |
10 |
3
|
| 2 |
11 |
5 |
16
|
|
- Liczby magicznego kwadratu można zastąpić odpowiadającymi im liczbami ze zbioru ciągów arytmetycznych o tej samej wspólnej różnicy między terminami r , tak że r × s = n 2 , i których początkowe terminy są również w ciągu arytmetycznym, aby uzyskać nienormalny magiczny kwadrat. Tutaj albo s albo r powinny być wielokrotnością n . Miejmy s ciąg arytmetyczny podane przez

- gdzie a jest wyrazem początkowym, c jest wspólną różnicą progresji arytmetycznych, a d jest wspólną różnicą między wyrazami początkowymi każdego progresji. Nowa magiczna stała będzie
![{\ Displaystyle M = na + {\ Frac {n} {2}} {\ duży [} (r-1) c + (s-1) d {\ duży]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1315a1e80e660caa150524368fc718884b56906e)
- Jeśli s = r = n , to mamy uproszczenie

- Jeśli dalej mamy a = c = 1 i d = n , otrzymujemy zwykłe M = n ( n 2 +1)/2. Dla danego M możemy znaleźć wymagane a , c i d rozwiązując liniowe równanie diofantyczne . W poniższych przykładach uporządkowaliśmy 4 normalne magiczne kwadraty po lewej stronie. Drugi kwadrat jest odpowiadającym nienormalnym magicznym kwadratem z r = 8, s = 2, a = 1, c = 1 i d = 10 takim, że nowa magiczna stała wynosi M = 38. Trzeci kwadrat to rząd 5 normalny magiczny kwadrat, który jest obróconą o 90 stopni w prawo wersją kwadratu wygenerowanego metodą De la Loubere. Po prawej stronie znajduje się odpowiedni nienormalny magiczny kwadrat z a = 4, c = 1 i d = 6 takim, że nowa magiczna stała wynosi M = 90.
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
| 1 |
17 |
16 |
4
|
| 14 |
6 |
7 |
11
|
| 8 |
12 |
13 |
5
|
| 15 |
3 |
2 |
18
|
|
| 11 |
10 |
4 |
23 |
17
|
| 18 |
12 |
6 |
5 |
24
|
| 25 |
19 |
13 |
7 |
1
|
| 2 |
21 |
20 |
14 |
8
|
| 9 |
3 |
22 |
16 |
15
|
|
| 16 |
14 |
7 |
30 |
23
|
| 24 |
17 |
10 |
8 |
31
|
| 32 |
25 |
18 |
11 |
4
|
| 5 |
28 |
26 |
19 |
12
|
| 13 |
6 |
29 |
22 |
20
|
|
- Każdy magiczny kwadrat można obracać i odbijać, tworząc 8 trywialnie odrębnych kwadratów. W teorii magicznych kwadratów wszystkie są ogólnie uważane za równoważne i mówi się, że osiem takich kwadratów tworzy pojedynczą klasę równoważności . Omawiając magiczne kwadraty, równoważne kwadraty zwykle nie są uważane za odrębne. 8 równoważnych kwadratów jest podanych poniżej dla magicznego kwadratu 3×3:
- Mając dowolny magiczny kwadrat, inny magiczny kwadrat tego samego rzędu może byćutworzony przez zamianęrządu i kolumny które przecinająsięw komórce po przekątnej z rzędemikolumnąprzecinającąsięw komórce komplementarnej (tzn.komórce symetrycznie naprzeciw środka ) o tej samej przekątnej. W przypadku równego kwadratu istnieje n /2 par wierszy i kolumn, które można zamienić; zatem możemy uzyskać 2 n /2 równoważne magiczne kwadraty, łącząc takie wymiany. W przypadku kwadratu nieparzystego istnieją ( n -1)/2 pary wierszy i kolumn, które można zamienić; i 2 ( n- 1)/2 równoważne magiczne kwadraty otrzymane przez połączenie takich wymian. Zamiana wszystkich wierszy i kolumn powoduje obrót kwadratu o 180 stopni. W przykładzie z użyciem magicznego kwadratu 4×4, lewy kwadrat jest oryginalnym kwadratem, podczas gdy prawy kwadrat jest nowym kwadratem uzyskanym przez zamianę pierwszego i czwartego rzędu i kolumn.
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
| 16 |
3 |
2 |
13
|
| 9 |
6 |
7 |
12
|
| 5 |
10 |
11 |
8
|
| 4 |
15 |
14 |
1
|
|
- Mając dowolny magiczny kwadrat, inny magiczny kwadrat tego samego rzędu może być utworzony przez zamianę dwóch rzędów po jednej stronie linii środkowej, a następnie zamianę odpowiednich dwóch rzędów po drugiej stronie linii środkowej; następnie zamieniając się jak kolumny. W przypadku kwadratu parzystego, ponieważ jest n /2 rzędów i kolumn o tej samej stronie, istnieje n ( n - 2)/8 par takich wierszy i kolumn, które można zamienić. W ten sposób możemy uzyskać 2 n ( n -2)/8 równoważnych magicznych kwadratów przez połączenie takich wymian. W przypadku kwadratu nieparzystego, ponieważ istnieje ( n - 1)/2 rzędy i kolumny o tej samej stronie, istnieje ( n - 1) ( n - 3)/8 par takich wierszy i kolumn, które można zamienić. Tak więc istnieje 2 ( n - 1)( n - 3)/8 równoważnych magicznych kwadratów uzyskanych przez połączenie takich wymian. Zamiana wszystkich możliwych par wierszy i kolumn powoduje obrót każdej ćwiartki kwadratu o 180 stopni. W przykładzie z użyciem magicznego kwadratu 4×4, lewy kwadrat jest oryginalnym kwadratem, podczas gdy prawy kwadrat jest nowym kwadratem uzyskanym przez tę transformację. W środkowym kwadracie rząd 1 został zamieniony z rządem 2; a wiersze 3 i 4 zostały zamienione. Ostatni kwadrat po prawej stronie uzyskuje się przez zamianę kolumn 1 i 2 oraz kolumn 3 i 4 środkowego kwadratu. W tym konkretnym przykładzie transformacja ta sprowadza się do obrócenia ćwiartek o 180 stopni. Środkowy kwadrat jest również kwadratem magicznym, ponieważ oryginalny kwadrat jest skojarzonym kwadratem magicznym.
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
| 12 |
6 |
7 |
9
|
| 1 |
15 |
14 |
4
|
| 13 |
3 |
2 |
16
|
| 8 |
10 |
11 |
5
|
|
| 6 |
12 |
9 |
7
|
| 15 |
1 |
4 |
14
|
| 3 |
13 |
16 |
2
|
| 10 |
8 |
5 |
11
|
|
- Magiczny kwadrat pozostaje magiczny, gdy którykolwiek z jego niecentralnych wierszy x i y zostanie zamieniony, wraz z wymianą ich uzupełniających się wierszy n - x + 1 i n - y + 1; a następnie zamieniając się jak kolumny. Jest to uogólnienie powyższych dwóch przekształceń. Gdy y = n - x + 1, ta transformacja redukuje się do pierwszej z dwóch powyższych transformacji. Gdy x i y znajdują się po tej samej stronie linii środkowej, ta transformacja redukuje się do drugiej z powyższych dwóch transformacji. W poniższym przykładzie pierwotny kwadrat znajduje się po lewej stronie, a ostatni kwadrat po prawej. Środkowy kwadrat został uzyskany przez zamianę rzędów 1 i 3 oraz rzędów 2 i 4 pierwotnego kwadratu. Ostatni kwadrat po prawej stronie uzyskuje się przez zamianę kolumn 1 i 3 oraz kolumn 2 i 4 środkowego kwadratu. W tym przykładzie ta transformacja sprowadza się do zamiany ćwiartek po przekątnej. Ponieważ pierwotny kwadrat jest skojarzony, środkowy kwadrat również jest magiczny.
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
|
| 11 |
5 |
8 |
10
|
| 2 |
16 |
13 |
3
|
| 14 |
4 |
1 |
15
|
| 7 |
9 |
12 |
6
|
|
- Magiczny kwadrat pozostaje magiczny, gdy jego kwadranty są zamienione po przekątnej. Odnosi się to dokładnie do równych kwadratów. W przypadku kwadratu o nieparzystym porządku należy zamienić połówki środkowego rzędu i środkowej kolumny. Przykłady parzystych i nieparzystych kwadratów podano poniżej:
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
| 11 |
5 |
8 |
10
|
| 2 |
16 |
13 |
3
|
| 14 |
4 |
1 |
15
|
| 7 |
9 |
12 |
6
|
|
| 17 |
24 |
1 |
8 |
15
|
| 23 |
5 |
7 |
14 |
16
|
| 4 |
6 |
13 |
20 |
22
|
| 10 |
12 |
19 |
21 |
3
|
| 11 |
18 |
25 |
2 |
9
|
|
| 21 |
3 |
19 |
10 |
12
|
| 2 |
9 |
25 |
11 |
18
|
| 20 |
22 |
13 |
4 |
6
|
| 8 |
15 |
1 |
17 |
24
|
| 14 |
16 |
7 |
23 |
5
|
|
Dla asocjacyjnych magicznych kwadratów
- Magiczny kwadrat asocjacyjny pozostaje asocjacyjny, gdy dwa rzędy lub kolumny w równej odległości od środka są zamienione miejscami. W przypadku równego kwadratu istnieje n /2 par wierszy lub kolumn, które można zamienić; zatem możemy otrzymać 2 n /2 × 2 n /2 = 2 n równoważnych magicznych kwadratów łącząc takie wymiany. W przypadku kwadratu nieparzystego istnieją ( n -1)/2 pary wierszy lub kolumn, które można zamienić; oraz 2 n- 1 równoważne magiczne kwadraty otrzymane przez połączenie takich wymian. Zamiana wszystkich rzędów powoduje odwrócenie kwadratu w pionie (tj. odbicie wzdłuż osi poziomej), podczas gdy zamiana wszystkich kolumn powoduje odwrócenie kwadratu w poziomie (tzn. odbicie wzdłuż osi pionowej). W poniższym przykładzie skojarzony magiczny kwadrat 4×4 po lewej stronie jest przekształcany w kwadrat po prawej stronie, zamieniając drugi i trzeci rząd, otrzymując słynny magiczny kwadrat Durera.
| 16 |
3 |
2 |
13
|
| 9 |
6 |
7 |
12
|
| 5 |
10 |
11 |
8
|
| 4 |
15 |
14 |
1
|
|
| 16 |
3 |
2 |
13
|
| 5 |
10 |
11 |
8
|
| 9 |
6 |
7 |
12
|
| 4 |
15 |
14 |
1
|
|
- Skojarzone magiczne kwadraty pozostają skojarzone, gdy dwa rzędy (lub kolumny) o tej samej stronie są zamienione z odpowiadającymi im rzędami (lub kolumnami) o innych bokach. W przypadku kwadratu parzystego, ponieważ jest n /2 rzędów (lub kolumn) o tej samej stronie, istnieje n ( n -2)/8 par takich wierszy (lub kolumn), które można zamienić. W ten sposób możemy uzyskać 2 n ( n -2)/8 × 2 n ( n -2)/8 = 2 n ( n -2)/4 równoważnych magicznych kwadratów przez połączenie takich wymian. W przypadku kwadratu nieparzystego, ponieważ istnieje ( n -1)/2 rzędy lub kolumny o tej samej stronie, istnieje ( n -1)( n -3)/8 par takich wierszy lub kolumn, które można zamienić. Zatem istnieje 2 ( n - 1)( n - 3)/8 × 2 ( n - 1)( n - 3)/8 = 2 ( n - 1)( n - 3)/4 równoważne magiczne kwadraty uzyskane przez łączenie takich węzłów. Zamiana wszystkich rzędów o tych samych bokach odwraca każdą ćwiartkę kwadratu w pionie, podczas gdy zamiana wszystkich kolumn o tych samych bokach odwraca każdą ćwiartkę kwadratu w poziomie. W poniższym przykładzie oryginalny kwadrat znajduje się po lewej stronie, którego rzędy 1 i 2 są zamienione ze sobą wraz z rzędami 3 i 4, aby otrzymać przekształcony kwadrat po prawej stronie.
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
| 12 |
6 |
7 |
9
|
| 1 |
15 |
14 |
4
|
| 13 |
3 |
2 |
16
|
| 8 |
10 |
11 |
5
|
|
Do pandiagonalnych magicznych kwadratów
- Magiczny kwadrat pandiagonalny pozostaje kwadratem magicznym pandiagonalnym przy cyklicznym przesuwaniu wierszy, kolumn lub obu. To pozwala nam umieścić podaną liczbę w dowolnej z n 2 komórek kwadratu rzędu n . Tak więc dla danego kwadratu pan-magicznego istnieje n 2 równoważnych kwadratów pan-magicznych. W poniższym przykładzie oryginalny kwadrat po lewej stronie jest przekształcany przez przesunięcie pierwszego rzędu na dół, aby uzyskać nowy kwadrat panoramy pośrodku. Następnie, pierwsza i druga kolumna środkowego kwadratu panmagicznego jest przesuwana kołowo w prawo, aby uzyskać nowy kwadrat panmagiczny po prawej stronie.
| 10 |
3 |
13 |
8
|
| 5 |
16 |
2 |
11
|
| 4 |
9 |
7 |
14
|
| 15 |
6 |
12 |
1
|
|
| 5 |
16 |
2 |
11
|
| 4 |
9 |
7 |
14
|
| 15 |
6 |
12 |
1
|
| 10 |
3 |
13 |
8
|
|
| 2 |
11 |
5 |
16
|
| 7 |
14 |
4 |
9
|
| 12 |
1 |
15 |
6
|
| 13 |
8 |
10 |
3
|
|
Dla obramowanych magicznych kwadratów
- Obramowany magiczny kwadrat pozostaje obramowanym magicznym kwadratem po permutacji komórek obramowania w wierszach lub kolumnach, wraz z odpowiadającymi im terminami uzupełniającymi, utrzymując stałe komórki narożne. Ponieważ komórki w każdym rzędzie i kolumnie każdej koncentrycznej granicy mogą być permutowane niezależnie, gdy rząd n ≥ 5 jest nieparzysty, istnieją ((n-2)! × (n-4)! × ··· × 3!) 2 równorzędne obramowane kwadraty. Gdy n ≥ 6 jest parzyste, istnieją ((n-2)! × (n-4)! × ··· × 4!) 2 równoważne obramowane kwadraty. W poniższym przykładzie podano kwadrat rzędu 5, którego wiersz graniczny został permutowany. Możemy otrzymać (3!) 2 = 36 takich równoważnych kwadratów.
| 1 |
23 |
16 |
4 |
21
|
| 15 |
14 |
7 |
18 |
11
|
| 24 |
17 |
13 |
9 |
2
|
| 20 |
8 |
19 |
12 |
6
|
| 5 |
3 |
10 |
22 |
25
|
|
| 1 |
16 |
23 |
4 |
21
|
| 15 |
14 |
7 |
18 |
11
|
| 24 |
17 |
13 |
9 |
2
|
| 20 |
8 |
19 |
12 |
6
|
| 5 |
10 |
3 |
22 |
25
|
|
- Obramowany magiczny kwadrat pozostaje obramowanym magicznym kwadratem po tym, jak każda z jego koncentrycznych granic zostanie niezależnie obrócona lub odbita względem centralnego kwadratu magicznego rdzenia. Jeśli istnieje b granic, to ta transformacja da 8 b równoważnych kwadratów. W poniższym przykładzie magicznego kwadratu 5×5 obramowanie zostało obrócone o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara.
| 1 |
23 |
16 |
4 |
21
|
| 15 |
14 |
7 |
18 |
11
|
| 24 |
17 |
13 |
9 |
2
|
| 20 |
8 |
19 |
12 |
6
|
| 5 |
3 |
10 |
22 |
25
|
|
| 21 |
11 |
2 |
6 |
25
|
| 4 |
14 |
7 |
18 |
22
|
| 16 |
17 |
13 |
9 |
10
|
| 23 |
8 |
19 |
12 |
3
|
| 1 |
15 |
24 |
20 |
5
|
|
Do złożonych magicznych kwadratów
- Złożony kwadrat magiczny pozostaje złożonym kwadratem magicznym, gdy osadzone kwadraty magiczne przechodzą transformacje, które nie naruszają właściwości magicznych (np. obrót, odbicie, przesuwanie wierszy i kolumn itd.).
Specjalne metody budowy
Na przestrzeni tysiącleci odkryto wiele sposobów tworzenia magicznych kwadratów. Metody te można sklasyfikować jako metody ogólne i metody specjalne w tym sensie, że metody ogólne pozwalają nam skonstruować więcej niż jeden magiczny kwadrat danego rzędu, podczas gdy metody specjalne pozwalają nam skonstruować tylko jeden magiczny kwadrat danego rzędu. Metody specjalne to specyficzne algorytmy, podczas gdy metody ogólne mogą wymagać pewnych prób i błędów.
Metody specjalne to standardowe i najprostsze sposoby na zbudowanie magicznego kwadratu. Podąża za pewnymi konfiguracjami / wzorami / algorytmem, który generuje regularne wzory liczb w kwadracie. Poprawność tych specjalnych metod można udowodnić za pomocą jednej z ogólnych metod podanych w dalszych rozdziałach. Po utworzeniu magicznego kwadratu przy użyciu specjalnej metody, transformacje opisane w poprzedniej sekcji można zastosować, aby uzyskać kolejne magiczne kwadraty. Metody specjalne są zwykle określane nazwiskiem autora(ów) (jeśli są znane), który opisał metodę, np. metoda De la Loubere'a, metoda Starchey'a, metoda Bachet'a itp.
Magiczne kwadraty istnieją dla wszystkich wartości n , z wyjątkiem rzędu 2. Magiczne kwadraty mogą być klasyfikowane według ich kolejności jako nieparzyste, podwójnie parzyste ( n podzielne przez cztery) i pojedynczo parzyste ( n parzyste, ale nie podzielne przez cztery). Ta klasyfikacja opiera się na fakcie, że do budowy tych różnych rodzajów kwadratów należy zastosować zupełnie inne techniki. Dziwne i podwójnie parzyste magiczne kwadraty są łatwe do wygenerowania; konstrukcja pojedynczo parzystych kwadratów magicznych jest trudniejsza, ale istnieje kilka metod, w tym metoda LUX dla magicznych kwadratów (dzięki Johnowi Hortonowi Conway ) i metoda Strachey dla magicznych kwadratów .
Metoda konstruowania magicznego kwadratu rzędu 3
W XIX wieku Édouard Lucas opracował ogólną formułę zamawiania 3 magicznych kwadratów. Rozważ poniższą tabelę złożoną z dodatnich liczb całkowitych a , b i c :
|
c − b
|
c + ( a + b ) |
c − a
|
|
c - ( a - b ) |
C |
c + ( a − b )
|
|
c + a
|
c − ( a + b ) |
c + b
|
Te dziewięć liczb będzie odrębnymi dodatnimi liczbami całkowitymi tworzącymi magiczny kwadrat o magicznej stałej 3 c , o ile 0 < a < b < c − a i b ≠ 2 a . Co więcej, każdy magiczny kwadrat 3×3 odrębnych dodatnich liczb całkowitych ma tę postać.
W 1997 Lee Sallows odkrył, że pomijając rotacje i odbicia, każdy wyraźny równoległobok narysowany na diagramie Arganda definiuje unikalny magiczny kwadrat 3×3 i vice versa, wynik, który nigdy wcześniej nie był odnotowany.
Metoda konstruowania magicznego kwadratu nieparzystego rzędu
Metodę konstruowania magicznych kwadratów nieparzystego rzędu opublikował francuski dyplomata de la Loubère w swojej książce Nowa historyczna relacja królestwa Syjamu (Du Royaume de Siam, 1693), w rozdziale zatytułowanym Problem magicznego kwadratu według Indian . Metoda działa w następujący sposób:
Metoda zaleca rozpoczęcie w środkowej kolumnie pierwszego rzędu cyfrą 1. Następnie podstawowy ruch wypełniania kwadratów odbywa się po przekątnej w górę iw prawo, krok po kroku. Jeśli napotkasz wypełnione pole, zamiast tego poruszasz się pionowo w dół o jedno pole, a następnie kontynuujesz jak poprzednio. Kiedy ruch "w górę iw prawo" opuściłby kwadrat, jest on zawijany odpowiednio do ostatniego rzędu lub pierwszej kolumny.
Możliwe jest rozpoczęcie od innych kwadratów, a nie od środkowej kolumny pierwszego rzędu, ale wtedy tylko sumy wierszy i kolumn będą identyczne i dadzą magiczną sumę, podczas gdy sumy przekątne będą się różnić. Wynik będzie więc kwadratem półmagicznym, a nie prawdziwym kwadratem magicznym. Poruszanie się w kierunkach innych niż północny wschód może również skutkować magicznymi kwadratami.
Zamówienie 3
| 8 |
1 |
6
|
| 3 |
5 |
7
|
| 4 |
9 |
2
|
|
Zamów 5
| 17 |
24 |
1 |
8 |
15
|
| 23 |
5 |
7 |
14 |
16
|
| 4 |
6 |
13 |
20 |
22
|
| 10 |
12 |
19 |
21 |
3
|
| 11 |
18 |
25 |
2 |
9
|
|
Zamówienie 9
| 47 |
58 |
69 |
80 |
1 |
12 |
23 |
34 |
45
|
| 57 |
68 |
79 |
9 |
11 |
22 |
33 |
44 |
46
|
| 67 |
78 |
8 |
10 |
21 |
32 |
43 |
54 |
56
|
| 77 |
7 |
18 |
20 |
31 |
42 |
53 |
55 |
66
|
| 6 |
17 |
19 |
30 |
41 |
52 |
63 |
65 |
76
|
| 16 |
27 |
29 |
40 |
51 |
62 |
64 |
75 |
5
|
| 26 |
28 |
39 |
50 |
61 |
72 |
74 |
4 |
15
|
| 36 |
38 |
49 |
60 |
71 |
73 |
3 |
14 |
25
|
| 37 |
48 |
59 |
70 |
81 |
2 |
13 |
24 |
35
|
|
Metoda konstruowania magicznego kwadratu podwójnie równomiernego porządku
Podwójnie parzysty oznacza, że n jest parzystą wielokrotnością parzystej liczby całkowitej; lub 4 p (np. 4, 8, 12), gdzie p jest liczbą całkowitą.
Wzór ogólny
Wszystkie liczby są zapisywane w kolejności od lewej do prawej w każdym rzędzie po kolei, zaczynając od lewego górnego rogu. Liczby są następnie albo zachowywane w tym samym miejscu, albo zamieniane z ich diametralnie przeciwnymi liczbami w pewien regularny wzór. W magicznym kwadracie rzędu czwartego liczby w czterech centralnych kwadratach i jednym kwadracie w każdym rogu są zachowywane w tym samym miejscu, a pozostałe są zamieniane z ich diametralnie przeciwnymi liczbami.
Konstrukcja magicznego kwadratu porządku 4
Zaczynając od góry po lewej, idź od lewej do prawej przez każdy rząd kwadratu, licząc każdą komórkę od 1 do 16 i wypełniając komórki wzdłuż przekątnych odpowiednią liczbą. Po dojściu do prawej dolnej komórki kontynuuj, przechodząc od prawej do lewej, zaczynając od prawego dolnego rogu tabeli przez każdy wiersz, i wypełnij komórki bez przekątnej, licząc od 1 do 16, odpowiednią liczbą. Jak pokazano niżej:
M = Zamówienie 4
| 1 |
|
|
4
|
|
6 |
7 |
|
|
10 |
11 |
|
| 13 |
|
|
16
|
|
M = Zamówienie 4
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
Rozszerzenie powyższego przykładu dla zamówień 8 i 12
Najpierw wygeneruj tabelę wzorców, w której „1” oznacza wybór z kwadratu, w którym liczby są zapisane w kolejności od 1 do n 2 (od lewej do prawej, od góry do dołu ), a „0” oznacza wybór z kwadratu, w którym liczby są zapisane w odwrotnej kolejności n 2 do 1. Dla M = 4, tabela wzorów jest pokazana poniżej (trzecia macierz od lewej). Kiedy zacieniamy niezmienione komórki (komórki z „1”), otrzymujemy wzór krzyżowy.
M = Zamówienie 4
| 1 |
2 |
3 |
4
|
| 5 |
6 |
7 |
8
|
| 9 |
10 |
11 |
12
|
| 13 |
14 |
15 |
16
|
|
M = Zamówienie 4
| 16 |
15 |
14 |
13
|
| 12 |
11 |
10 |
9
|
| 8 |
7 |
6 |
5
|
| 4 |
3 |
2 |
1
|
|
M = Zamówienie 4
| 1 |
0 |
0 |
1
|
| 0 |
1 |
1 |
0
|
| 0 |
1 |
1 |
0
|
| 1 |
0 |
0 |
1
|
|
M = Zamówienie 4
| 1 |
15 |
14 |
4
|
| 12 |
6 |
7 |
9
|
| 8 |
10 |
11 |
5
|
| 13 |
3 |
2 |
16
|
|
Wzorce są następujące: a) w każdym wierszu i kolumnie jest taka sama liczba jedynek i zer; b) każdy wiersz i każda kolumna są „palindromiczne”; c) lewa i prawa połowa są odbiciami lustrzanymi; oraz d) górna i dolna połowa są lustrzanymi odbiciami (cid oznaczają b). Tablica wzorców może być oznaczona za pomocą heksadecymalnych jako (9, 6, 6, 9) dla uproszczenia (1-nibble na wiersz, 4 wiersze). Najprostszą metodą generowania wymaganego wzoru dla kwadratów o podwójnej parzystości wyższego rzędu jest skopiowanie ogólnego wzoru dla kwadratu czwartego rzędu w każdym podkwadracie cztery na cztery.
Dla M = 8 możliwe wybory dla wzorca to (99, 66, 66, 99, 99, 66, 66, 99); (3C, 3C, C3, C3, C3, C3, 3C, 3C); (A5, 5A, A5, 5A, 5A, A5, 5A, A5) (2-nible w rzędzie, 8 rzędów).
M = Zamówienie 8
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
1
|
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
0
|
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
0
|
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
1
|
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
1
|
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
0
|
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
0
|
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
1
|
|
M = Zamówienie 8
| 1 |
|
|
4 |
5 |
|
|
8
|
|
10 |
11 |
|
|
14 |
15 |
|
|
18 |
19 |
|
|
22 |
23 |
|
| 25 |
|
|
28 |
29 |
|
|
32
|
| 33 |
|
|
36 |
37 |
|
|
40
|
|
42 |
43 |
|
|
46 |
47 |
|
|
50 |
51 |
|
|
54 |
55 |
|
| 57 |
|
|
60 |
61 |
|
|
64
|
|
M = Zamówienie 8
| 1 |
63 |
62 |
4 |
5 |
59 |
58 |
8
|
| 56 |
10 |
11 |
53 |
52 |
14 |
15 |
49
|
| 48 |
18 |
19 |
45 |
44 |
22 |
23 |
41
|
| 25 |
39 |
38 |
28 |
29 |
35 |
34 |
32
|
| 33 |
31 |
30 |
36 |
37 |
27 |
26 |
40
|
| 24 |
42 |
43 |
21 |
20 |
46 |
47 |
17
|
| 16 |
50 |
51 |
13 |
12 |
54 |
55 |
9
|
| 57 |
7 |
6 |
60 |
61 |
3 |
2 |
64
|
|
Dla M = 12, tabela wzorców (E07, E07, E07, 1F8, 1F8, 1F8, 1F8, 1F8, 1F8, E07, E07, E07) daje magiczny kwadrat (3-nibble na rząd, 12 rzędów). można policzyć liczbę wyborów na podstawie tabeli wzorców z uwzględnieniem symetrii obrotowych.
Metoda superpozycji
Najwcześniejszego odkrycia metody superpozycji dokonał indyjski matematyk Narayana w XIV wieku. Ta sama metoda została później ponownie odkryta i zbadana na początku XVIII wieku w Europie przez de la Loubere, Poignarda, de La Hire i Sauveura; a metoda ta jest zwykle określana jako metoda de la Hire. Chociaż praca Eulera nad magicznym kwadratem była nieoryginalna, słynął z przypuszczenia, że niemożliwe jest skonstruowanie równo nieparzystych, uporządkowanych, wzajemnie ortogonalnych kwadratów grecko-łacińskich . Przypuszczenie to zostało obalone w połowie XX wieku. Dla jasności ekspozycji wyróżniliśmy dwie ważne odmiany tej metody.
Metoda Eulera
Metoda ta polega na skonstruowaniu dwóch wstępnych kwadratów, które po zsumowaniu dają magiczny kwadrat. Jako bieżący przykład rozważymy magiczny kwadrat 3×3. Każdą liczbę z naturalnego kwadratu 3×3 możemy jednoznacznie oznaczyć parą liczb jako
|
|
| αa |
αb |
αc
|
| βa |
βb |
βc
|
| ya |
γb |
γc
|
|
gdzie każda para alfabetów greckiego i łacińskiego, np. αa , ma być sumowana , czyli αa = α + a . Tutaj ( α , β , γ ) = (0, 3, 6) i ( a , b , c ) = (1, 2, 3). Liczby 0, 3 i 6 są określane jako liczby pierwiastkowe, natomiast liczby 1, 2 i 3 są określane jako liczby podstawowe . Ważnym ogólnym ograniczeniem jest tutaj:
-
litera grecka jest połączona z literą łacińską tylko raz .
W ten sposób pierwotny kwadrat można teraz podzielić na dwa prostsze kwadraty:
Kwadraty z literami są określane jako kwadrat grecki lub kwadrat łaciński, jeśli są wypełnione odpowiednio literami greckimi lub łacińskimi. Magiczny kwadrat można zbudować, upewniając się, że kwadraty greckie i łacińskie również są kwadratami magicznymi. Odwrotność tego stwierdzenia jest również często, ale nie zawsze (np. obramowane kwadraty magiczne), prawdziwa: kwadrat magiczny można rozłożyć na kwadrat grecki i łaciński, które same są kwadratami magicznymi. Tak więc metoda jest przydatna zarówno do syntezy, jak i analizy kwadratu magicznego. Wreszcie, badając wzorzec, w którym liczby są ułożone w gotowym kwadracie, często można wymyślić szybszy algorytm do skonstruowania kwadratów wyższego rzędu, które odwzorowują dany wzorzec, bez konieczności tworzenia wstępnego greki i łaciny. kwadraty.
Podczas konstruowania magicznego kwadratu 3×3, kwadraty greckie i łacińskie z tylko trzema unikalnymi terminami są znacznie łatwiejsze do pokonania niż oryginalny kwadrat z dziewięcioma różnymi terminami. Suma wierszy i suma kolumn kwadratu greckiego będą takie same, α + β + γ , jeśli
-
każda litera pojawia się dokładnie raz w danej kolumnie lub wierszu .
Można to osiągnąć poprzez cykliczne permutacji z alfa , beta i gamma . Spełnienie tych dwóch warunków zapewnia, że wynikowy kwadrat jest kwadratem półmagicznym; i mówi się, że takie greckie i łacińskie kwadraty są wzajemnie prostopadłe do siebie. Dla danego rzędu n jest co najwyżej n -1 kwadratów w zestawie wzajemnie prostopadłych kwadratów, nie licząc zmian wynikających z permutacji symboli. Ta górna granica jest dokładna, gdy n jest liczbą pierwszą.
Aby skonstruować magiczny kwadrat, powinniśmy również upewnić się, że przekątne sumują się do magicznej stałej. W tym celu mamy trzeci warunek:
-
albo wszystkie litery powinny pojawić się dokładnie raz na obu przekątnych; lub w przypadku kwadratów nieparzystych, jedna z przekątnych powinna składać się w całości ze środkowego wyrazu, a druga przekątna powinna mieć wszystkie litery dokładnie raz .
O prostopadłych do siebie kwadratach greckich i łacińskich, które spełniają pierwszą część trzeciego warunku (że wszystkie litery występują na obu przekątnych) mówimy, że są to kwadraty grecko-łacińskie o podwójnej przekątnej, które są wzajemnie ortogonalne .
Nieparzyste kwadraty: Dla nieparzystego kwadratu 3×3, ponieważ α , β i γ są w postępie arytmetycznym, ich suma jest równa iloczynowi rzędu kwadratu i członu środkowego, tj. α + β + γ = 3 β . Zatem sumy przekątne będą równe, jeśli mamy β s na głównej przekątnej i α , β , γ na skośnej przekątnej. Podobnie dla kwadratu łacińskiego. Otrzymane kwadraty greckie i łacińskie oraz ich kombinacje będą jak poniżej. Kwadrat łaciński to tylko obrót o 90 stopni w kierunku przeciwnym do ruchu wskazówek zegara względem kwadratu greckiego (lub równoważnie, obracanie się wokół osi pionowej) z zamienionymi odpowiednimi literami. Zastąpienie wartości literami greckimi i łacińskimi da magiczny kwadrat 3×3.
|
|
|
| βc |
αa |
γb
|
| ya |
βb |
αc
|
| αb |
γc |
βa
|
|
|
W przypadku kwadratów nieparzystych metoda ta wyjaśnia, dlaczego działa metoda syjamska (metoda De la Loubere) i jej warianty. Ta podstawowa metoda może być użyta do skonstruowania nieparzystych magicznych kwadratów wyższych rzędów. Podsumować:
- W przypadku kwadratów o nieparzystym porządku, aby skonstruować kwadrat grecki, umieść wyraz środkowy wzdłuż głównej przekątnej, a pozostałe wyrazy wzdłuż przekątnej ukośnej. Pozostałe puste komórki są wypełniane ruchami ukośnymi. Kwadrat łaciński można zbudować, obracając lub odwracając kwadrat grecki i zastępując odpowiednie alfabety. Magiczny kwadrat uzyskuje się przez dodanie kwadratów greckich i łacińskich.
Osobliwością metody konstrukcji podanej powyżej dla nieparzystych magicznych kwadratów jest to, że środkowa liczba ( n 2 + 1)/2 zawsze pojawi się w środkowej komórce magicznego kwadratu. Ponieważ są ( n - 1)! Sposoby ułożenia skośnych terminów przekątnych możemy uzyskać ( n - 1)! W ten sposób greckie kwadraty; to samo z kwadratami łacińskimi. Ponadto, ponieważ każdy kwadrat grecki może być sparowany z ( n - 1)! Kwadraty łacińskie, a ponieważ dla każdego z kwadratów greckich wyraz środkowy można umieścić dowolnie na głównej przekątnej lub skośnej przekątnej (i odpowiednio wzdłuż skośnej przekątnej lub głównej przekątnej dla kwadratów łacińskich), możemy skonstruować w sumie 2 × ( n - 1)! × ( n - 1)! magiczne kwadraty przy użyciu tej metody. Dla n = 3, 5 i 7 da to odpowiednio 8, 1152 i 1036,800 różnych magicznych kwadratów. Dzieląc przez 8, aby pominąć równoważne kwadraty spowodowane obrotem i odbiciami, otrzymujemy odpowiednio 1,144 i 129,600 zasadniczo różnych magicznych kwadratów.
Jako inny przykład podana jest konstrukcja magicznego kwadratu 5×5. Liczby są pisane bezpośrednio w miejsce alfabetów. Ponumerowane kwadraty są nazywane kwadratami podstawowymi lub pierwiastkami, jeśli są wypełnione odpowiednio liczbami podstawowymi lub liczbami pierwiastkowymi. Liczby są umieszczane wokół skośnej przekątnej w kwadracie tak, że środkowa kolumna wynikowego pierwiastka ma 0, 5, 10, 15, 20 (od dołu do góry). Podstawowy kwadrat uzyskuje się przez obrócenie pierwiastka w lewo o 90 stopni i zastąpienie liczb. Wynikowy kwadrat jest asocjacyjnym kwadratem magicznym, w którym każda para liczb symetrycznie przeciwna do środka sumuje się do tej samej wartości, 26. Np. 16+10, 3+23, 6+20 itd. W gotowym kwadracie , 1 jest umieszczana w środkowej komórce dolnego rzędu, a kolejne liczby są umieszczane poprzez wydłużony ruch skoczka (dwie komórki po prawej, dwie komórki w dół) lub równoważnie ruch gońca (dwie komórki po przekątnej w prawo). Kiedy dochodzi do kolizji, ruch przerwania polega na przesunięciu jednej komórki w górę. Wszystkie liczby nieparzyste znajdują się wewnątrz środkowego rombu utworzonego przez 1, 5, 25 i 21, natomiast liczby parzyste znajdują się w rogach. Występowanie liczb parzystych można wywnioskować, kopiując kwadrat na sąsiednie boki. Liczby parzyste z czterech sąsiednich kwadratów utworzą krzyż.
|
|
| 10 |
|
|
0 |
5
|
|
10 |
|
20 |
0
|
| 0 |
|
10 |
|
|
|
0 |
|
10 |
|
| 15 |
|
0 |
|
10
|
|
| 10 |
15 |
20 |
0 |
5
|
| 5 |
10 |
15 |
20 |
0
|
| 0 |
5 |
10 |
15 |
20
|
| 20 |
0 |
5 |
10 |
15
|
| 15 |
20 |
0 |
5 |
10
|
|
| 2 |
1 |
5 |
4 |
3
|
| 1 |
5 |
4 |
3 |
2
|
| 5 |
4 |
3 |
2 |
1
|
| 4 |
3 |
2 |
1 |
5
|
| 3 |
2 |
1 |
5 |
4
|
|
| 12 |
16 |
25 |
4 |
8
|
| 6 |
15 |
19 |
23 |
2
|
| 5 |
9 |
13 |
17 |
21
|
| 24 |
3 |
7 |
11 |
20 |
24
|
| 18 |
22 |
1 |
10 |
14 |
18 |
22
|
|
|
|
4 |
8 |
12 |
16
|
|
|
|
|
2 |
6
|
|
Poniżej podano odmianę powyższego przykładu, w której ukośną sekwencję przekątną przyjęto w innej kolejności. Powstały magiczny kwadrat jest odwróconą wersją słynnego magicznego kwadratu Marsa Agryppy. Jest to skojarzeniowy kwadrat magiczny i jest taki sam jak ten wytworzony metodą Moschopoulosa. Tutaj wynikowy kwadrat zaczyna się od 1 umieszczonego w komórce, która znajduje się na prawo od środkowej komórki, i postępuje zgodnie z metodą De la Loubere, z ruchem w dół w prawo. W przypadku kolizji ruch rozbijający polega na przesunięciu dwóch komórek w prawo.
|
|
| 10 |
0 |
15 |
5 |
20
|
| 20 |
10 |
0 |
15 |
5
|
| 5 |
20 |
10 |
0 |
15
|
| 15 |
5 |
20 |
10 |
0
|
| 0 |
15 |
5 |
20 |
10
|
|
| 1 |
4 |
2 |
5 |
3
|
| 4 |
2 |
5 |
3 |
1
|
| 2 |
5 |
3 |
1 |
4
|
| 5 |
3 |
1 |
4 |
2
|
| 3 |
1 |
4 |
2 |
5
|
|
| 11 |
4 |
17 |
10 |
23
|
| 24 |
12 |
5 |
18 |
6
|
| 7 |
25 |
13 |
1 |
19
|
| 20 |
8 |
21 |
14 |
2
|
| 3 |
16 |
9 |
22 |
15
|
|
W poprzednich przykładach, dla kwadratu greckiego, drugi rząd można uzyskać z pierwszego rzędu, przesuwając go kołowo w prawo o jedną komórkę. Podobnie trzeci rząd jest kołowo przesuniętą wersją drugiego rzędu o jedną komórkę w prawo; i tak dalej. Podobnie rzędy kwadratu łacińskiego są przesunięte w lewo o jedną komórkę. Przesunięcia rzędów dla kwadratów greckiego i łacińskiego są wzajemnie przeciwne. Możliwe jest kołowe przesuwanie wierszy o więcej niż jedną komórkę, aby utworzyć kwadrat grecki i łaciński.
- W przypadku kwadratów o nieparzystym porządku, których kolejność nie jest podzielna przez trzy, możemy stworzyć kwadraty greckie, przesuwając rząd o dwa miejsca w lewo lub w prawo, tworząc kolejny rząd. Kwadrat łaciński tworzy się poprzez odwrócenie kwadratu greckiego wzdłuż głównej przekątnej i zamianę odpowiednich liter. Daje nam to kwadrat łaciński, którego rzędy tworzy się poprzez przesunięcie rzędu w kierunku przeciwnym do kierunku kwadratu greckiego. Kwadrat grecki i kwadrat łaciński należy sparować w taki sposób, aby przesunięcia ich rzędów były wzajemnie przeciwne. Magiczny kwadrat uzyskuje się przez dodanie kwadratów greckich i łacińskich. Kiedy kolejność jest również liczbą pierwszą, ta metoda zawsze tworzy pandiagonalny kwadrat magiczny.
To zasadniczo odtwarza ruch rycerza. Wszystkie litery pojawią się na obu przekątnych, zapewniając prawidłową sumę przekątnych. Ponieważ istnieje n ! permutacje liter greckich, za pomocą których możemy utworzyć pierwszy rząd kwadratu greckiego, jest więc n ! Greckie kwadraty, które można tworzyć, przesuwając pierwszy rząd w jednym kierunku. Podobnie istnieje n ! takie kwadraty łacińskie tworzone przez przesunięcie pierwszego rzędu w przeciwnym kierunku. Ponieważ kwadrat grecki może być połączony z dowolnym kwadratem łacińskim z przesunięciem w przeciwnych rzędach, istnieje n ! × n ! takie kombinacje. Wreszcie, ponieważ grecki kwadrat można utworzyć, przesuwając wiersze w lewo lub w prawo, jest w sumie 2 × n ! × n ! magiczne kwadraty, które można utworzyć tą metodą. Dla n = 5 i 7, ponieważ są to liczby pierwsze, ta metoda tworzy 28 800 i 50 803 200 pandiagonalnych magicznych kwadratów. Dzieląc przez 8, aby pominąć równoważne kwadraty spowodowane obrotem i odbiciami, otrzymujemy 3600 i 6350400 równoważnych kwadratów. Dalsze dzielenie przez n 2, aby pominąć równoważne kwadraty panmagiczne z powodu cyklicznego przesuwania wierszy lub kolumn, otrzymujemy 144 i 129 600 zasadniczo różnych kwadratów panmagicznych. Dla zamówienia 5 kwadratów są to jedyne dostępne kwadraty panmagiczne. Warunek, że rząd kwadratu nie jest podzielny przez 3 oznacza, że nie możemy skonstruować kwadratów rzędu 9, 15, 21, 27 itd. tą metodą.
W poniższym przykładzie kwadrat został skonstruowany tak, że 1 znajduje się w środkowej komórce. W gotowym kwadracie liczby mogą być wyliczane w sposób ciągły ruchem skoczka (dwie komórki w górę, jedna komórka po prawej). Kiedy dochodzi do kolizji, ruch przerywający polega na przesunięciu o jedną komórkę w górę, o jedną komórkę w lewo. Wynikowy kwadrat to kwadratowy magiczny kwadrat. Ten kwadrat ma również inną diabelską właściwość, że dowolne pięć komórek we wzorze kwinkunksa utworzonego przez dowolny nieparzysty podkwadrat, w tym zawinięcie, sumuje się do stałej magicznej 65. Na przykład 13+7+1+20+24, 23+ 1+9+15+17, 13+21+10+19+2 itd. Również cztery rogi dowolnego kwadratu 5×5 i komórki środkowej, a także komórki środkowe z każdej strony wraz z komórką środkową, w tym zawiń, podaj magiczną sumę: 13+10+19+22+1 i 20+24+12+8+1. Wreszcie cztery romboidy tworzące wydłużone krzyże również dają magiczną sumę: 23+1+9+24+8, 15+1+17+20+12, 14+1+18+13+19, 7+1+25+ 22+10.
| 10 |
15 |
20 |
0 |
5
|
| 0 |
5 |
10 |
15 |
20
|
| 15 |
20 |
0 |
5 |
10
|
| 5 |
10 |
15 |
20 |
0
|
| 20 |
0 |
5 |
10 |
15
|
|
| 3 |
1 |
4 |
2 |
5
|
| 4 |
2 |
5 |
3 |
1
|
| 5 |
3 |
1 |
4 |
2
|
| 1 |
4 |
2 |
5 |
3
|
| 2 |
5 |
3 |
1 |
4
|
|
| 13 |
16 |
24 |
2 |
10
|
| 4 |
7 |
15 |
18 |
21
|
| 20 |
23 |
1 |
9 |
12
|
| 6 |
14 |
17 |
25 |
3
|
| 22 |
5 |
8 |
11 |
19
|
|
Możemy również łączyć kwadraty greckie i łacińskie konstruowane różnymi metodami. W poniższym przykładzie, podstawowe pole jest wykonane ruchem skoczka. Odtworzyliśmy magiczny kwadrat uzyskany metodą De la Loubere. Tak jak poprzednio, możemy utworzyć 8 × ( n - 1)! × n ! magiczne kwadraty przez tę kombinację. Dla n = 5 i 7 stworzy to 23 040 i 29 030 400 magicznych kwadratów. Po podzieleniu przez 8 w celu pominięcia równoważnych kwadratów z powodu rotacji i odbicia otrzymujemy 2880 i 3628800 kwadratów.
| 15 |
20 |
0 |
5 |
10
|
| 20 |
0 |
5 |
10 |
15
|
| 0 |
5 |
10 |
15 |
20
|
| 5 |
10 |
15 |
20 |
0
|
| 10 |
15 |
20 |
0 |
5
|
|
| 2 |
4 |
1 |
3 |
5
|
| 3 |
5 |
2 |
4 |
1
|
| 4 |
1 |
3 |
5 |
2
|
| 5 |
2 |
4 |
1 |
3
|
| 1 |
3 |
5 |
2 |
4
|
|
| 17 |
24 |
1 |
8 |
15
|
| 23 |
5 |
7 |
14 |
16
|
| 4 |
6 |
13 |
20 |
22
|
| 10 |
12 |
19 |
21 |
3
|
| 11 |
18 |
25 |
2 |
9
|
|
Dla rzędu 5 kwadratów te trzy metody dają pełny spis liczby magicznych kwadratów, które można zbudować metodą superpozycji. Pomijając rotację i odbicia, całkowita liczba magicznych kwadratów rzędu 5 wytworzonych metodą superpozycji wynosi 144 + 3600 + 2880 = 6624.
Kwadraty parzyste: W ten sposób możemy również skonstruować kwadraty parzyste. Ponieważ w alfabecie greckim i łacińskim nie ma terminu pośredniego dla równych kwadratów, oprócz dwóch pierwszych ograniczeń, aby sumy przekątne dawały stałą magiczną, wszystkie litery alfabetu powinny pojawić się na głównej przekątnej i na pochylić przekątną.
Przykład kwadratu 4×4 podano poniżej. Dla danej przekątnej i skośnej przekątnej w kwadracie greckim, pozostałe komórki można wypełnić pod warunkiem, że każda litera występuje tylko raz w rzędzie i kolumnie.
|
|
| α |
β |
γ |
δ
|
| γ |
δ |
α |
β
|
| δ |
γ |
β |
α
|
| β |
α |
δ |
γ
|
|
| a |
b |
C |
D
|
| D |
C |
b |
a
|
| b |
a |
D |
C
|
| C |
D |
a |
b
|
|
| αa |
βb |
γc |
d
|
| γd |
c |
αb |
βa
|
| b |
ya |
βd |
αc
|
| βc |
αd |
a |
γb
|
|
| 1 |
6 |
11 |
16
|
| 12 |
15 |
2 |
5
|
| 14 |
9 |
8 |
3
|
| 7 |
4 |
13 |
10
|
|
Używając tych dwóch grecko-łacińskich kwadratów, możemy skonstruować 2 × 4! × 4! = 1152 magicznych kwadratów. Dzieląc przez 8, aby wyeliminować równoważne kwadraty spowodowane obrotem i odbiciami, otrzymujemy 144 zasadniczo różne magiczne kwadraty rzędu 4. Są to jedyne magiczne kwadraty, które można skonstruować metodą Eulera, ponieważ są tylko dwa wzajemnie prostopadłe, podwójnie przekątne grecko-łacińskie kwadraty zamówienie 4.
Podobnie magiczny kwadrat 8×8 może być skonstruowany jak poniżej. Tutaj kolejność pojawiania się liczb nie jest ważna; jednak kwadranty imitują wzór układu grecko-łacińskich kwadratów 4×4.
| 0 |
8 |
16 |
24 |
32 |
40 |
48 |
56
|
| 24 |
16 |
8 |
0 |
56 |
48 |
40 |
32
|
| 48 |
56 |
32 |
40 |
16 |
24 |
0 |
8
|
| 40 |
32 |
56 |
48 |
8 |
0 |
24 |
16
|
| 56 |
48 |
40 |
32 |
24 |
16 |
8 |
0
|
| 32 |
40 |
48 |
56 |
0 |
8 |
16 |
24
|
| 8 |
0 |
24 |
16 |
40 |
32 |
56 |
48
|
| 16 |
24 |
0 |
8 |
48 |
56 |
32 |
40
|
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8
|
| 3 |
4 |
1 |
2 |
7 |
8 |
5 |
6
|
| 5 |
6 |
7 |
8 |
1 |
2 |
3 |
4
|
| 7 |
8 |
5 |
6 |
3 |
4 |
1 |
2
|
| 4 |
3 |
2 |
1 |
8 |
7 |
6 |
5
|
| 2 |
1 |
4 |
3 |
6 |
5 |
8 |
7
|
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1
|
| 6 |
5 |
8 |
7 |
2 |
1 |
4 |
3
|
|
| 1 |
10 |
19 |
28 |
37 |
46 |
55 |
64
|
| 27 |
20 |
9 |
2 |
63 |
56 |
45 |
38
|
| 53 |
62 |
39 |
48 |
17 |
26 |
3 |
12
|
| 47 |
40 |
61 |
54 |
11 |
4 |
25 |
18
|
| 60 |
51 |
42 |
33 |
32 |
23 |
14 |
5
|
| 34 |
41 |
52 |
59 |
6 |
13 |
24 |
31
|
| 16 |
7 |
30 |
21 |
44 |
35 |
58 |
49
|
| 22 |
29 |
8 |
15 |
50 |
57 |
36 |
43
|
|
Metoda Eulera dała początek badaniu kwadratów grecko-łacińskich . Metoda Eulera konstruowania magicznych kwadratów jest ważna dla dowolnej kolejności z wyjątkiem 2 i 6.
Wariacje : Magiczne kwadraty zbudowane z wzajemnie ortogonalnych kwadratów grecko-łacińskich o podwójnej przekątnej są interesujące same w sobie, ponieważ właściwość magiczna wyłania się ze względnej pozycji alfabetów w kwadracie, a nie z żadnej arytmetycznej właściwości przypisanej im wartości. Oznacza to, że alfabetom takich kwadratów możemy przypisać dowolną wartość i nadal uzyskać magiczny kwadrat. Jest to podstawa do konstruowania kwadracików wyświetlających pewne informacje (np. urodziny, lata itp.) w kwadracie oraz tworzenia "kwadratów odwracalnych". Na przykład możemy wyświetlić liczbę π ≈3,141 592 w dolnym rzędzie magicznego kwadratu 4×4 przy użyciu kwadratu grecko-łacińskiego podanego powyżej przez przypisanie ( α , β , γ , δ ) = (10, 0, 90, 15) i ( a , b , c , d ) = (0, 2, 3, 4). Otrzymamy następujący nienormalny magiczny kwadrat o magicznej sumie 124:
| 10 |
2 |
93 |
19
|
| 94 |
18 |
12 |
0
|
| 17 |
90 |
4 |
13
|
| 3 |
14 |
15 |
92
|
Metoda Narayana-De la Hire dla równych zamówień
Metoda Narayana-De la Hire dla nieparzystego kwadratu jest taka sama jak metoda Eulera. Jednak dla parzystych kwadratów odrzucamy drugi wymóg, aby każda litera grecka i łacińska pojawiała się tylko raz w danym wierszu lub kolumnie. Pozwala nam to wykorzystać fakt, że suma ciągu arytmetycznego o parzystej liczbie wyrazów jest równa sumie dwóch przeciwnych wyrazów symetrycznych pomnożonej przez połowę całkowitej liczby wyrazów. Tak więc, konstruując kwadraty greckie lub łacińskie,
-
w przypadku równych kwadratów, litera może pojawić się n /2 razy w kolumnie, ale tylko raz z rzędu lub odwrotnie.
Bieżący przykład, jeśli weźmiemy kwadrat 4×4, gdzie terminy greckie i łacińskie mają wartości ( α , β , γ , δ ) = (0, 4, 8, 12) i ( a , b , c , d ) = (1, 2, 3, 4), odpowiednio, to mamy α + β + γ + δ = 2 ( α + δ ) = 2 ( β + γ ). Podobnie a + b + c + d = 2 ( a + d ) = 2 ( b + c ). Oznacza to, że komplementarna para α i δ (lub β i γ ) może pojawić się dwukrotnie w kolumnie (lub wierszu) i nadal dawać pożądaną magiczną sumę. W ten sposób możemy skonstruować:
-
W przypadku równych kwadratów, grecki magiczny kwadrat tworzy się, umieszczając najpierw alfabety greckie na głównej przekątnej w pewnej kolejności. Skośna przekątna jest następnie wypełniana w tej samej kolejności lub przez wybranie terminów, które są komplementarne do terminów na głównej przekątnej. Wreszcie pozostałe komórki są wypełniane kolumnowo. Dla danej kolumny używamy terminów komplementarnych w przekątnych komórkach przecinanych przez tę kolumnę, upewniając się, że pojawiają się one tylko raz w danym wierszu, ale n /2 razy w danej kolumnie. Kwadrat łaciński uzyskuje się przez odwrócenie lub obrócenie kwadratu greckiego i zamianę odpowiednich alfabetów. Ostateczny magiczny kwadrat uzyskuje się przez dodanie kwadratów greckich i łacińskich.
W poniższym przykładzie główną przekątną (od lewego górnego do prawego dolnego rogu) wypełnia się kolejnością uporządkowaną jako α , β , γ , δ , natomiast przekątną skośną (od lewego dolnego do prawego górnego) w tej samej kolejności. Pozostałe komórki są następnie wypełniane kolumnowo tak, że litery uzupełniające pojawiają się tylko raz w rzędzie, ale dwa razy w kolumnie. W pierwszej kolumnie, ponieważ α pojawia się w 1. i 4. wierszu, pozostałe komórki wypełnia się jego wyrazem dopełniającym δ . Podobnie puste komórki w drugiej kolumnie są wypełnione γ ; w trzeciej kolumnie β ; i czwarta kolumna a . Każda grecka litera pojawia się tylko raz w rzędach, a dwukrotnie w kolumnach. Jako takie, sumy wierszy to α + β + γ + δ, podczas gdy sumy kolumn to 2 ( α + δ ) lub 2 ( β + γ ). Podobnie jest w przypadku kwadratu łacińskiego, który uzyskuje się poprzez odwrócenie kwadratu greckiego wzdłuż głównej przekątnej i zamianę odpowiednich liter.
|
|
| α |
γ |
β |
δ
|
| δ |
β |
γ |
α
|
| δ |
β |
γ |
α
|
| α |
γ |
β |
δ
|
|
| a |
D |
D |
a
|
| C |
b |
b |
C
|
| b |
C |
C |
b
|
| D |
a |
a |
D
|
|
| αa |
γd |
βd |
a
|
| c |
βb |
γb |
αc
|
| b |
βc |
γc |
αb
|
| αd |
ya |
βa |
d
|
|
| 1 |
12 |
8 |
13
|
| 15 |
6 |
10 |
3
|
| 14 |
7 |
11 |
2
|
| 4 |
9 |
5 |
16
|
|
Powyższy przykład wyjaśnia, dlaczego metoda „krzyżowania” dla podwójnie nawet magicznego kwadratu działa. Kolejny możliwy magiczny kwadrat 4×4, który jest również ukośny, a także najbardziej doskonały, jest skonstruowany poniżej przy użyciu tej samej zasady. Jednak ciąg diagonalny jest tak dobrany, że wszystkie cztery litery α , β , γ , δ znajdują się wewnątrz centralnego podkwadratu 2x2. Pozostałe komórki są wypełniane kolumnowo tak, że każda litera pojawia się tylko raz w rzędzie. W pierwszej kolumnie puste komórki należy wypełnić jedną z liter wybranych z pary komplementarnej α i δ . Biorąc pod uwagę pierwszą kolumnę, wpis w drugim rzędzie może być tylko δ, ponieważ α jest już tam w drugim rzędzie; podczas gdy w trzecim rzędzie wpisem może być tylko α, ponieważ δ jest już obecne w trzecim rzędzie. Postępujemy podobnie, aż wszystkie komórki zostaną wypełnione. Podany poniżej kwadrat łaciński został uzyskany przez odwrócenie kwadratu greckiego wzdłuż głównej przekątnej i zastąpienie alfabetów greckich odpowiednimi alfabetami łacińskimi.
|
|
| α |
β |
δ |
γ
|
| δ |
γ |
α |
β
|
| α |
β |
δ |
γ
|
| δ |
γ |
α |
β
|
|
| a |
D |
a |
D
|
| b |
C |
b |
C
|
| D |
a |
D |
a
|
| C |
b |
C |
b
|
|
| αa |
βd |
a |
γd
|
| b |
γc |
αb |
βc
|
| αd |
βa |
d |
ya
|
| c |
γb |
αc |
βb
|
|
| 1 |
8 |
13 |
12
|
| 14 |
11 |
2 |
7
|
| 4 |
5 |
16 |
9
|
| 15 |
10 |
3 |
6
|
|
Możemy użyć tego podejścia do konstruowania pojedynczych, nawet magicznych kwadratów. Jednak w tym przypadku musimy być bardziej ostrożni, ponieważ kryteria jednoznacznego parowania alfabetów greckiego i łacińskiego nie są automatycznie spełnione. Naruszenie tego warunku prowadzi do braku niektórych liczb w ostatnim kwadracie, podczas gdy inne duplikują się. Oto ważne zastrzeżenie:
- W przypadku pojedynczych równych kwadratów w kwadracie greckim sprawdź komórki kolumn, które są sparowane w pionie z jego uzupełnieniem. W takim przypadku odpowiednia komórka kwadratu łacińskiego musi zawierać tę samą literę, co jej poziomo sparowana komórka.
Poniżej znajduje się konstrukcja magicznego kwadratu 6×6, w którym podane są liczby, a nie alfabety. Drugi kwadrat jest tworzony przez odwrócenie pierwszego kwadratu wzdłuż głównej przekątnej. Tutaj w pierwszej kolumnie pierwiastka kwadratowego trzecia komórka jest sparowana z jej uzupełnieniem w czwartej komórce. Tak więc w kwadracie podstawowym liczby w 1. i 6. komórce trzeciego rzędu są takie same. Podobnie z innymi kolumnami i wierszami. W tym przykładzie odwrócona wersja pierwiastka spełnia ten warunek.
| 0 |
24 |
18 |
12 |
6 |
30
|
| 30 |
6 |
12 |
18 |
24 |
0
|
| 0 |
24 |
12 |
18 |
6 |
30
|
| 30 |
24 |
12 |
18 |
6 |
0
|
| 30 |
6 |
18 |
12 |
24 |
0
|
| 0 |
6 |
18 |
12 |
24 |
30
|
|
| 1 |
6 |
1 |
6 |
6 |
1
|
| 5 |
2 |
5 |
5 |
2 |
2
|
| 4 |
3 |
3 |
3 |
4 |
4
|
| 3 |
4 |
4 |
4 |
3 |
3
|
| 2 |
5 |
2 |
2 |
5 |
5
|
| 6 |
1 |
6 |
1 |
1 |
6
|
|
| 1 |
30 |
19 |
18 |
12 |
31
|
| 35 |
8 |
17 |
23 |
26 |
2
|
| 4 |
27 |
15 |
21 |
10 |
34
|
| 33 |
28 |
16 |
22 |
9 |
3
|
| 32 |
11 |
20 |
14 |
29 |
5
|
| 6 |
7 |
24 |
13 |
25 |
36
|
|
Jako kolejny przykład tak skonstruowanego magicznego kwadratu 6×6 podano poniżej. Tutaj wpisy ukośne są ułożone inaczej. Podstawowy kwadrat jest tworzony przez odwrócenie pierwiastka po głównej przekątnej. W drugim kwadracie zastrzeżenie dotyczące pojedynczo parzystego kwadratu nie jest spełnione, co prowadzi do nienormalnego kwadratu magicznego (trzeciego kwadratu), w którym liczby 3, 13, 24 i 34 są zduplikowane, ale brakuje liczb 4, 18, 19 i 33.
| 6 |
30 |
12 |
18 |
0 |
24
|
| 24 |
0 |
12 |
18 |
30 |
6
|
| 24 |
0 |
18 |
12 |
30 |
6
|
| 6 |
30 |
18 |
12 |
0 |
24
|
| 24 |
0 |
18 |
12 |
30 |
6
|
| 6 |
30 |
12 |
18 |
0 |
24
|
|
| 2 |
5 |
5 |
2 |
5 |
2
|
| 6 |
1 |
1 |
6 |
1 |
6
|
| 3 |
3 |
4 |
4 |
4 |
3
|
| 4 |
4 |
3 |
3 |
3 |
4
|
| 1 |
6 |
6 |
1 |
6 |
1
|
| 5 |
2 |
2 |
5 |
2 |
5
|
|
| 8 |
35 |
17 |
20 |
5 |
26
|
| 30 |
1 |
13 |
24 |
31 |
12
|
| 27 |
3 |
22 |
16 |
34 |
9
|
| 10 |
34 |
21 |
15 |
3 |
28
|
| 25 |
6 |
24 |
13 |
36 |
7
|
| 11 |
32 |
14 |
23 |
2 |
29
|
|
Ostatni warunek jest nieco arbitralny i nie zawsze musi być wywoływany, jak w tym przykładzie, gdzie w pierwiastku każda komórka jest sparowana w pionie ze swoim uzupełnieniem:
| 6 |
30 |
12 |
24 |
18 |
0
|
| 6 |
0 |
18 |
24 |
12 |
30
|
| 24 |
0 |
12 |
6 |
18 |
30
|
| 6 |
30 |
18 |
24 |
12 |
0
|
| 24 |
30 |
12 |
6 |
18 |
0
|
| 24 |
0 |
18 |
6 |
12 |
30
|
|
| 2 |
2 |
5 |
2 |
5 |
5
|
| 6 |
1 |
1 |
6 |
6 |
1
|
| 3 |
4 |
3 |
4 |
3 |
4
|
| 5 |
5 |
2 |
5 |
2 |
2
|
| 4 |
3 |
4 |
3 |
4 |
3
|
| 1 |
6 |
6 |
1 |
1 |
6
|
|
| 8 |
32 |
17 |
26 |
23 |
5
|
| 12 |
1 |
19 |
30 |
18 |
31
|
| 27 |
4 |
15 |
10 |
21 |
34
|
| 11 |
35 |
20 |
29 |
14 |
2
|
| 28 |
33 |
16 |
9 |
22 |
3
|
| 25 |
6 |
24 |
7 |
13 |
36
|
|
Jako jeszcze jeden przykład, wygenerowaliśmy magiczny kwadrat 8×8. W przeciwieństwie do krzyżowego wzoru we wcześniejszej sekcji dla równomiernie równego kwadratu, tutaj mamy szachownicę dla zmienionych i niezmienionych komórek. Ponadto w każdym kwadrancie liczby nieparzyste i parzyste pojawiają się w naprzemiennych kolumnach.
| 0 |
48 |
16 |
32 |
24 |
40 |
8 |
56
|
| 56 |
8 |
40 |
24 |
32 |
16 |
48 |
0
|
| 0 |
48 |
16 |
32 |
24 |
40 |
8 |
56
|
| 56 |
8 |
40 |
24 |
32 |
16 |
48 |
0
|
| 56 |
8 |
40 |
24 |
32 |
16 |
48 |
0
|
| 0 |
48 |
16 |
32 |
24 |
40 |
8 |
56
|
| 56 |
8 |
40 |
24 |
32 |
16 |
48 |
0
|
| 0 |
48 |
16 |
32 |
24 |
40 |
8 |
56
|
|
| 1 |
8 |
1 |
8 |
8 |
1 |
8 |
1
|
| 7 |
2 |
7 |
2 |
2 |
7 |
2 |
7
|
| 3 |
6 |
3 |
6 |
6 |
3 |
6 |
3
|
| 5 |
4 |
5 |
4 |
4 |
5 |
4 |
5
|
| 4 |
5 |
4 |
5 |
5 |
4 |
5 |
4
|
| 6 |
3 |
6 |
3 |
3 |
6 |
3 |
6
|
| 2 |
7 |
2 |
7 |
7 |
2 |
7 |
2
|
| 8 |
1 |
8 |
1 |
1 |
8 |
1 |
8
|
|
| 1 |
56 |
17 |
40 |
32 |
41 |
16 |
57
|
| 63 |
10 |
47 |
26 |
34 |
23 |
50 |
7
|
| 3 |
54 |
19 |
38 |
30 |
43 |
14 |
59
|
| 61 |
12 |
45 |
28 |
36 |
21 |
42 |
5
|
| 60 |
13 |
44 |
29 |
37 |
20 |
53 |
4
|
| 6 |
51 |
22 |
35 |
27 |
46 |
11 |
62
|
| 58 |
15 |
42 |
31 |
39 |
18 |
55 |
2
|
| 8 |
47 |
24 |
33 |
25 |
48 |
9 |
64
|
|
Wariacje : Możliwych jest wiele wariacji podstawowej idei: para komplementarna może pojawić się w kolumnie n /2 razy lub mniej . Oznacza to, że kolumna kwadratu greckiego może być skonstruowana przy użyciu więcej niż jednej pary komplementarnej. Ta metoda pozwala nam nasycić magiczny kwadrat znacznie bogatszymi właściwościami. Pomysł można również rozszerzyć na przekątne. Poniżej podano przykład magicznego kwadratu 8×8. W gotowym kwadracie każdy z czterech kwadrantów jest również kwadratami panmagicznymi, każdy kwadrant ma taką samą stałą magiczną 130.
| 0 |
48 |
56 |
8 |
16 |
32 |
40 |
24
|
| 56 |
8 |
0 |
48 |
40 |
24 |
16 |
32
|
| 0 |
48 |
56 |
8 |
16 |
32 |
40 |
24
|
| 56 |
8 |
0 |
48 |
40 |
24 |
16 |
32
|
| 48 |
0 |
8 |
56 |
32 |
16 |
24 |
40
|
| 8 |
56 |
48 |
0 |
24 |
40 |
32 |
16
|
| 48 |
0 |
8 |
56 |
32 |
16 |
24 |
40
|
| 8 |
56 |
48 |
0 |
24 |
40 |
32 |
16
|
|
| 1 |
8 |
1 |
8 |
7 |
2 |
7 |
2
|
| 7 |
2 |
7 |
2 |
1 |
8 |
1 |
8
|
| 8 |
1 |
8 |
1 |
2 |
7 |
2 |
7
|
| 2 |
7 |
2 |
7 |
8 |
1 |
8 |
1
|
| 3 |
6 |
3 |
6 |
5 |
4 |
5 |
4
|
| 5 |
4 |
5 |
4 |
3 |
6 |
3 |
6
|
| 6 |
3 |
6 |
3 |
4 |
5 |
4 |
5
|
| 4 |
5 |
4 |
5 |
6 |
3 |
6 |
3
|
|
| 1 |
56 |
57 |
16 |
23 |
34 |
47 |
26
|
| 63 |
10 |
7 |
50 |
41 |
32 |
17 |
40
|
| 8 |
49 |
64 |
9 |
18 |
39 |
42 |
31
|
| 58 |
15 |
2 |
55 |
48 |
25 |
24 |
33
|
| 51 |
6 |
11 |
62 |
37 |
20 |
29 |
44
|
| 13 |
60 |
53 |
4 |
27 |
46 |
35 |
22
|
| 54 |
3 |
14 |
59 |
36 |
21 |
28 |
45
|
| 12 |
61 |
52 |
5 |
30 |
43 |
38 |
19
|
|
Metoda granic
Metoda obramowania dla zamówienia 3
W tej metodzie celem jest owinięcie ramki wokół mniejszego magicznego kwadratu, który służy jako rdzeń. Rozważmy na przykład kwadrat 3×3. Odejmując środkową liczbę 5 od każdej liczby 1, 2, ..., 9, otrzymujemy 0, ± 1, ± 2, ± 3 i ± 4, co z braku lepszych słów zrobimy za S. Harry White , odnoszą się do liczby kości. Magiczna stała magicznego kwadratu, który będziemy nazywać szkieletem, utworzonym przez te liczby kości będzie wynosić zero, ponieważ dodanie wszystkich rzędów magicznego kwadratu da nM = Σ k = 0; zatem M = 0.
Nietrudno argumentować, że środkowa liczba powinna być umieszczona w środkowej komórce: niech x będzie liczbą umieszczoną w środkowej komórce, wtedy suma środkowej kolumny, środkowego rzędu i dwóch przekątnych daje Σ k + 3 x = 4 mln . Ponieważ Σ k = 3 M , mamy x = M / 3. Tutaj M = 0, więc x = 0.
Umieszczając środkową liczbę 0 w środkowej komórce, chcemy skonstruować granicę tak, aby wynikowy kwadrat był magiczny. Niech granicę poda:
Ponieważ suma każdego wiersza, kolumny i przekątnych musi być stałą (czyli zero), mamy
-
a + a* = 0,
-
b + b* = 0,
-
u + u* = 0,
-
v + v* = 0.
Teraz, jeśli wybraliśmy a , b , u i v , to mamy a* = - a , b* = - b , u* = - u , i v* = - v . Oznacza to, że jeśli przypiszemy daną liczbę do zmiennej, powiedzmy a = 1, to jej uzupełnienie zostanie przypisane do a* , czyli a* = - 1. Tak więc z ośmiu nieznanych zmiennych wystarczy podać wartość tylko cztery zmienne. Rozważymy a , b , u i v jako zmienne niezależne, natomiast a* , b* , u* i v* jako zmienne zależne. To pozwala nam traktować liczbę kości ± x jako pojedynczą liczbę niezależnie od znaku, ponieważ (1) jej przypisanie do danej zmiennej, powiedzmy a , automatycznie implikuje, że ta sama liczba o przeciwnym znaku będzie współdzielona z jej uzupełnieniem a* , oraz (2) dwóm niezależnym zmiennym, powiedzmy a i b , nie można przypisać tego samego numeru kości. Ale jak wybrać a , b , u i v ? Mamy sumę górnego wiersza i sumę prawej kolumny jako
-
u + a + v = 0,
-
v + b + u* = 0.
Ponieważ 0 jest liczbą parzystą, są tylko dwa sposoby, aby suma trzech liczb całkowitych dała liczbę parzystą: 1) jeśli wszystkie trzy były parzyste, lub 2) jeśli dwie były nieparzyste, a jedna była parzysta. Ponieważ w naszym wyborze liczb mamy tylko dwie liczby parzyste niezerowe (± 2 i ± 4), pierwsze stwierdzenie jest fałszywe. Zatem musi być tak, że drugie zdanie jest prawdziwe: że dwie liczby są nieparzyste, a jedna parzysta.
Jedynym sposobem, w jaki oba powyższe równania mogą jednocześnie spełnić ten warunek parzystości i nadal być spójne ze zbiorem liczb, który mamy, jest sytuacja, gdy u i v są nieparzyste. Wręcz przeciwnie, gdybyśmy założyli, że u i a są nieparzyste, a v jest parzyste w pierwszym równaniu, to u* = - u będzie nieparzyste w drugim równaniu, czyniąc b również nieparzystym, aby spełnić warunek warunek parzystości. Wymaga to jednak trzech liczb nieparzystych ( u , a i b ), co przeczy faktowi, że mamy tylko dwie liczby nieparzyste (± 1 i ± 3), których możemy użyć. To dowodzi, że nieparzyste liczby kości zajmują komórki narożne. Po przeliczeniu na normalne liczby przez dodanie 5 oznacza to, że wszystkie rogi magicznego kwadratu 3×3 są zajęte przez liczby parzyste.
Tak więc, biorąc u = 1 i v = 3, mamy a = - 4 i b = - 2. Zatem gotowy kwadrat szkieletu będzie taki jak po lewej stronie. Dodając 5 do każdej liczby, otrzymujemy gotowy magiczny kwadrat.
Podobny argument można wykorzystać do skonstruowania większych kwadratów. Ponieważ nie istnieje magiczny kwadrat 2×2, wokół którego można by otoczyć ramkę, aby skonstruować magiczny kwadrat 4×4, kolejna najmniejsza kolejność, dla której możemy skonstruować obramowany kwadrat, to kolejność 5.
Metoda obramowania dla zamówienia 5
Rozważ kwadrat piątego rzędu. Do tego mamy magiczny rdzeń 3×3, wokół którego owiniemy magiczną ramkę. Stosowane liczby kości wyniosą ± 5, ± 6, ± 7, ± 8, ± 9, ± 10, ± 11 i ± 12. Pomijając znaki, mamy 8 numerów kości, z których 4 są parzyste i 4 z których są dziwne. Ogólnie rzecz biorąc, dla kwadratu dowolnego rzędu n będą 4( n -1) komórek granicznych, które należy wypełnić za pomocą 2( n -1) liczb kości. Niech magiczna granica zostanie podana jako
| ty |
a |
b |
C |
v
|
| D* |
|
|
|
D
|
| mi* |
|
|
|
mi
|
| F* |
|
|
|
F
|
| v* |
a* |
b* |
C* |
ty*
|
Tak jak poprzednio, powinniśmy
- umieść liczbę kości i jej dopełnienie naprzeciwko siebie, tak aby magiczna suma wynosiła zero.
Aby opisać magiczną granicę, wystarczy wyznaczyć liczby u, v, a, b, c, d, e, f . Tak jak poprzednio, mamy dwa równania ograniczające dla górnego wiersza i prawej kolumny:
-
u + a + b + c + v = 0
-
v + d + e + f + u* = 0.
Możliwych jest wiele rozwiązań. Standardowa procedura to:
- najpierw spróbuj określić komórki narożne, po czym spróbujemy określić resztę granicy.
Istnieje 28 sposobów wyboru dwóch liczb ze zbioru 8 liczb kości dla komórek narożnych u i v . Jednak nie wszystkie pary są dopuszczalne. Wśród 28 par 16 par składa się z parzystej i nieparzystej liczby, 6 par ma obie liczby parzyste, a 6 par ma obie liczby nieparzyste.
Możemy udowodnić, że komórki narożne u i v nie mogą mieć liczby parzystej i nieparzystej. Dzieje się tak dlatego, że gdyby tak było, wówczas sumy u + v i v + u* będą nieparzyste, a ponieważ 0 jest liczbą parzystą, sumy a + b + c oraz d + e + f również powinny być nieparzyste. Jedyny sposób, w jaki suma trzech liczb całkowitych da w wyniku liczbę nieparzystą, to: 1) dwie z nich są parzyste, a jedna nieparzysta, lub 2) gdy wszystkie trzy są nieparzyste. Ponieważ zakłada się, że komórki narożne są nieparzyste i parzyste, żadne z tych dwóch stwierdzeń nie jest zgodne z faktem, że mamy do dyspozycji tylko 3 parzyste i 3 nieparzyste liczby kości. To dowodzi, że u i v nie mogą mieć różnej parzystości. Eliminuje to 16 możliwości.
Używając podobnego wnioskowania o typach możemy również wyciągnąć pewne wnioski dotyczące zbiorów { a , b , c } i { d , e , f }. Jeśli u i v są parzyste, to oba zestawy powinny mieć dwie liczby nieparzyste i jedną parzystą. Jeśli u i v są nieparzyste, to jeden z zestawów powinien mieć trzy liczby parzyste, podczas gdy drugi zestaw powinien mieć jedną parzystą i dwie nieparzyste.
Jako bieżący przykład rozważmy przypadek, w którym zarówno u, jak i v są parzyste. 6 możliwych par to: (6, 8), (6, 10), (6, 12), (8, 10), (8, 12) i (10, 12). Ponieważ sumy u + v i v + u* są parzyste, sumy a + b + c oraz d + e + f również powinny być parzyste. Jedyny sposób, w jaki suma trzech liczb całkowitych da w wyniku liczbę parzystą, to: 1) dwie z nich są nieparzyste, a jedna parzysta, lub 2) gdy wszystkie trzy są parzyste. Fakt, że dwie komórki narożne są parzyste oznacza, że mamy do dyspozycji tylko 2 liczby parzyste. Zatem drugie stwierdzenie nie jest zgodne z tym faktem. Zatem musi być tak, że pierwsze zdanie jest prawdziwe: dwie z trzech liczb powinny być nieparzyste, a jedna parzysta.
Niech a, b, d, e będą liczbami nieparzystymi, a c i f będą liczbami parzystymi. Biorąc pod uwagę nieparzyste liczby kości, którymi dysponujemy: ± 5, ± 7, ± 9 i ± 11, ich różnice wahają się od D = {± 2, ± 4, ± 6}, a ich sumy wahają się od S = {± 12, ± 14, ± 16, ± 18, ± 20}. Przydatne jest również posiadanie tabeli ich sum i różnic do późniejszego wykorzystania. Teraz, biorąc pod uwagę komórki narożne ( u , v ), możemy sprawdzić jego dopuszczalność, sprawdzając, czy sumy u + v + c i v + u* + f mieszczą się w zbiorze D lub S . Dopuszczalność numerów narożnych jest warunkiem koniecznym, ale niewystarczającym, aby rozwiązanie zaistniało.
Na przykład, jeśli weźmiemy pod uwagę parę ( u , v ) = (8, 12), to u + v = 20 i v + u* = 6; i będziemy mieli do dyspozycji ± 6 i ± 10 parzystych liczb kości. Biorąc c = ± 6, mamy sumę u + v + c wynoszącą 26 i 14, w zależności od przyjętego znaku ± 6 , z których oba nie należą do zbiorów D lub S . Podobnie, biorąc c = ± 10, mamy sumę u + v + c wynoszącą 30 i 10, z których oba ponownie nie należą do zbiorów D lub S . Zatem para (8, 12) jest niedopuszczalna. W podobnym toku rozumowania możemy również wykluczyć parę (6, 12).
Jako inny przykład, jeśli weźmiemy pod uwagę parę ( u , v ) = (10, 12), wtedy u + v = 22 i v + u* = 2; i będziemy mieli do dyspozycji ± 6 i ± 8 parzystych liczb kostnych. Biorąc c = ± 6, mamy sumę u + v + c wynoszącą 28 i 16. Podczas gdy 28 nie należy do zbioru D ani S , 16 należy do zbioru S . Poprzez inspekcję stwierdzamy, że jeśli ( a , b ) = (-7, -9), to a + b = -16; i spełni pierwsze równanie ograniczające. Ponadto, biorąc f = ± 8, mamy sumę v + u* + f równą 10 i -6. Podczas gdy 10 nie należy do zestawów D lub S , -6 należy do zestawu D . Od -7 do -9 zostały przypisane i B wyraźnie ( d , e ) = (-5, 11) tak, że d + e = 6; i spełni drugie równanie ograniczające.
Podobnie, biorąc c = ± 8, mamy sumę u + v + c wynoszącą 30 i 14. Podczas gdy 30 nie należy do zbioru D ani S , 14 należy do zbioru S . Podczas inspekcji stwierdzamy, że jeśli ( a , b ) = (-5, -9), to a + b = -14. Również biorąc f = ± 6, mamy sumę v + u* + f równą 8 i -4. Podczas gdy 8 nie należy do zestawów D lub S , -4 należy do zestawu D . Oczywiście, ( d , e ) = (-7, 11) tak, że d + e = 4 i drugie równanie więzów będzie spełnione.
Stąd para narożna ( u , v ) = (10, 12) jest dopuszczalna; i dopuszcza dwa rozwiązania: (a, b, c, d, e, f) = (-7, -9, -6, -5, 11, -8) oraz (a, b, c, d, e, f) = (-5, -9, -8, -7, 11, -6). Gotowe kwadraty szkieletowe podano poniżej. Magiczny kwadrat uzyskuje się przez dodanie 13 do każdej komórki.
| 10 |
-7 |
-9 |
-6 |
12
|
| 5 |
|
|
|
-5
|
| -11 |
|
|
|
11
|
| 8 |
|
|
|
-8
|
| -12 |
7 |
9 |
6 |
-10
|
|
| 23 |
6 |
4 |
7 |
25
|
| 18 |
|
|
|
8
|
| 2 |
|
|
|
24
|
| 21 |
|
|
|
5
|
| 1 |
20 |
22 |
19 |
3
|
|
| 10 |
-5 |
-9 |
-8 |
12
|
| 7 |
|
|
|
-7
|
| -11 |
|
|
|
11
|
| 6 |
|
|
|
-6
|
| -12 |
5 |
9 |
8 |
-10
|
|
| 23 |
8 |
4 |
5 |
25
|
| 20 |
|
|
|
6
|
| 2 |
|
|
|
24
|
| 19 |
|
|
|
7
|
| 1 |
18 |
22 |
21 |
3
|
|
Stosując podobny proces rozumowania, możemy skonstruować poniższą tabelę dla wartości u, v, a, b, c, d, e, f wyrażonych jako liczby kości, jak podano poniżej. Istnieje tylko 6 możliwych wyborów dla komórek narożnych, co prowadzi do 10 możliwych rozwiązań granicznych.
|
ty, v
|
a, b, c
|
d, e, f
|
| 12, 10 |
-6, -7, -9 |
-11, 5, 8
|
| 12, 10 |
-5, -8, -9 |
-11, 6, 7
|
| 11, 5 |
6, -10, -12 |
-9, 7, 8
|
| 10, 6 |
5, -9, -12 |
-11, 7, 8
|
| 10, 6 |
7, -11, -12 |
-9, 5, 8
|
| 9, 7 |
5, -10, -11 |
-12, 6, 8
|
| 9, 7 |
6, -10, -12 |
-11, 5, 8
|
| 8, 6 |
7, -10, -11 |
-12, 5, 9
|
| 8, 6 |
9, -11, -12 |
-10, 5, 7
|
| 7, 5 |
9, -10, -11 |
-12, 6, 8
|
Mając tę grupę 10 granic, możemy skonstruować 10×8×(3!) 2 = 2880 zasadniczo różnych graniczących magicznych kwadratów. Tutaj liczby kości ± 5, ..., ± 12 były następujące po sobie. Bardziej obramowane kwadraty można zbudować, jeśli liczby nie są kolejne. Jeśli użyto również nienastępujących po sobie numerów kości, to w sumie istnieje 605 magicznych granic. Tak więc całkowita liczba rzędu 5 zasadniczo różniących się granicami magicznych kwadratów (z kolejnymi i niekolejnymi liczbami) wynosi 174 240. Zobacz historię. Warto zauważyć, że liczba magicznych kwadratów piątego rzędu możliwych do skonstruowania metodą graniczną jest około 26 razy większa niż metodą superpozycji.
Metody liczenia ciągłego
Wyczerpujące wyliczenie wszystkich granic kwadratu magicznego danej kolejności, jak to zrobiono wcześniej, jest bardzo żmudne. Z tego powodu często pożądane jest rozwiązanie strukturalne, które pozwala na skonstruowanie obramowania dla kwadratu dowolnego rzędu. Poniżej podajemy trzy algorytmy konstruowania granicy dla nieparzystych, podwójnie parzystych i pojedyńczych parzystych kwadratów. Te algorytmy ciągłego wyliczania zostały odkryte w X wieku przez arabskich uczonych; a ich najwcześniej zachowana ekspozycja pochodzi z dwóch traktatów al-Buzjaniego i al-Antakiego, chociaż oni sami nie byli odkrywcami. Od tego czasu odkryto znacznie więcej takich algorytmów.
Nieparzyste uporządkowane kwadraty : Oto algorytm podany przez al-Buzjaniego do skonstruowania granicy nieparzystych kwadratów. Osobliwością tej metody jest to, że dla kwadratu rzędu n dwa sąsiednie rogi to liczby n - 1 i n + 1 .
Zaczynając od komórki nad lewym dolnym rogiem, umieszczamy liczby naprzemiennie w lewej kolumnie i dolnym rzędzie, aż dojdziemy do środkowej komórki. Następna liczba jest zapisywana w środkowej komórce dolnego właśnie osiągniętego wiersza, po czym wypełniamy komórkę w lewym górnym rogu, następnie środkową komórkę prawej kolumny, a następnie prawy górny róg. Następnie, zaczynając od już wypełnionej komórki powyżej środkowej komórki prawej kolumny, wznawiamy naprzemienne umieszczanie liczb w prawej kolumnie i górnym rzędzie. Gdy połowa komórek granicznych jest wypełniona, druga połowa jest wypełniana liczbami komplementarnymi do przeciwległych komórek. Kolejne granice wewnętrzne wypełnia się w ten sam sposób, aż do wypełnienia kwadratu rzędu 3.
Poniżej znajduje się przykład dla kwadratu dziewiątego rzędu.
| 8 |
80 |
78 |
76 |
75 |
12 |
14 |
16 |
10
|
| 67 |
22 |
64 |
62 |
61 |
26 |
28 |
24 |
15
|
| 69 |
55 |
32 |
52 |
51 |
36 |
34 |
27 |
13
|
| 71 |
57 |
47 |
38 |
45 |
40 |
35 |
25 |
11
|
| 73 |
59 |
49 |
43 |
41 |
39 |
33 |
23 |
9
|
| 5 |
19 |
29 |
42 |
37 |
44 |
53 |
63 |
77
|
| 3 |
17 |
48 |
30 |
31 |
46 |
50 |
65 |
79
|
| 1 |
58 |
18 |
20 |
21 |
56 |
54 |
60 |
81
|
| 72 |
2 |
4 |
6 |
7 |
70 |
68 |
66 |
74
|
Podwójna kolejność : Poniższa metoda jest podana przez al-Antaki. Rozważmy pustą granicę rzędu n = 4 k przy k ≥ 3. Osobliwością tego algorytmu jest to, że sąsiednie komórki narożne są zajęte przez liczby n i n - 1 .
Zaczynając od komórki w lewym górnym rogu, umieszczamy kolejne liczby w grupach po cztery, pierwsza obok rogu, druga i trzecia na dole, a czwarta na górze i tak dalej, aż zostanie w górny rząd (bez rogów) sześć pustych komórek. Następnie piszemy kolejne dwie liczby powyżej i kolejne cztery poniżej. Następnie wypełniamy górne rogi, najpierw z lewej, potem z prawej. Kolejną liczbę umieszczamy poniżej prawego górnego rogu w prawej kolumnie, kolejną liczbę po drugiej stronie w lewej kolumnie. Następnie wznawiamy umieszczanie grup czterech kolejnych liczb w dwóch kolumnach, jak poprzednio. Gdy połowa komórek granicznych jest wypełniona, druga połowa jest wypełniana liczbami komplementarnymi do przeciwległych komórek.
Poniższy przykład podaje granicę dla zamówienia 16 kwadratów.
| 15 |
1 |
255 |
254 |
4 |
5 |
251 |
250 |
8 |
9 |
10 |
246 |
245 |
244 |
243 |
16
|
| 240 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
|
| 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
239
|
| 19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
238
|
| 237 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
|
| 236 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21
|
| 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
235
|
| 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
234
|
| 233 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24
|
| 232 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25
|
| 26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
231
|
| 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
230
|
| 229 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28
|
| 228 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29
|
| 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
227
|
| 241 |
256 |
2 |
3 |
253 |
252 |
6 |
7 |
249 |
248 |
247 |
11 |
12 |
13 |
14 |
242
|
W przypadku zamówienia 8 kwadratów po prostu zaczynamy bezpośrednio od sześciu komórek.
| 7 |
1 |
2 |
62 |
61 |
60 |
59 |
8
|
| 56 |
|
|
|
|
|
|
9
|
| 10 |
|
|
|
|
|
|
55
|
| 11 |
|
|
|
|
|
|
54
|
| 53 |
|
|
|
|
|
|
12
|
| 52 |
|
|
|
|
|
|
13
|
| 14 |
|
|
|
|
|
|
51
|
| 57 |
64 |
63 |
3 |
4 |
5 |
6 |
58
|
Pojedynczo parzysty porządek : W przypadku pojedynczo parzystego porządku mamy algorytm podany przez al-Antaki. Tutaj komórki narożne są zajęte przez n i n - 1. Poniżej znajduje się przykład kwadratu dziesiątego rzędu.
Zacznij od umieszczenia 1 w dolnym rzędzie obok lewej komórki narożnej, a następnie umieść 2 w górnym rzędzie. Następnie umieść 3 w dolnym rzędzie i obróć obramowanie w kierunku przeciwnym do ruchu wskazówek zegara, umieszczając kolejne liczby, aż w prawej kolumnie zostanie osiągnięte n -2. Kolejne dwie liczby znajdują się w górnych rogach ( n - 1 w lewym górnym rogu i n w prawym górnym rogu). Następnie w lewej kolumnie umieszczamy kolejne dwie liczby, po czym wznawiamy cykliczne umieszczanie liczb, aż do wypełnienia połowy wszystkich komórek granicznych. Gdy połowa komórek granicznych jest wypełniona, druga połowa jest wypełniona liczbami komplementarnymi do przeciwległych komórek.
| 9 |
100 |
2 |
98 |
5 |
94 |
88 |
15 |
84 |
10
|
| 83 |
|
|
|
|
|
|
|
|
18
|
| 16 |
|
|
|
|
|
|
|
|
85
|
| 87 |
|
|
|
|
|
|
|
|
14
|
| 12 |
|
|
|
|
|
|
|
|
89
|
| 11 |
|
|
|
|
|
|
|
|
90
|
| 93 |
|
|
|
|
|
|
|
|
8
|
| 6 |
|
|
|
|
|
|
|
|
95
|
| 97 |
|
|
|
|
|
|
|
|
4
|
| 91 |
1 |
99 |
3 |
96 |
7 |
13 |
86 |
17 |
92
|
Sposób kompozycji
Dla kwadratów rzędu m × n, gdzie m , n > 2
Jest to metoda przypominająca iloczyn Kroneckera dwóch macierzy, która buduje magiczny kwadrat nm × nm z magicznego kwadratu n × n i magicznego kwadratu m × m . Iloczyn dwóch magicznych kwadratów tworzy magiczny kwadrat wyższego rzędu niż dwie wielokrotności. Niech dwa magiczne kwadraty będą rzędu m i n . Ostatni kwadrat będzie rzędu m × n . Podziel kwadrat rzędu m × n na m × m podkwadratów tak, aby było w sumie n 2 takich podkwadratów. W kwadracie porządku n zmniejsz o 1 wartość wszystkich liczb. Pomnóż te zredukowane wartości przez m 2 i umieść wyniki w odpowiednich podkwadratach całego kwadratu m × n . Kwadraty rzędu m są dodawane n 2 razy do podkwadratów ostatniego kwadratu. Osobliwością tej metody konstrukcji jest to, że każdy magiczny podkwadrat będzie miał różne sumy magiczne. Kwadrat utworzony z takich magicznych sum z każdego magicznego podkwadratu znów będzie magicznym kwadratem. Najmniejszy złożony magiczny kwadrat rzędu 9, składający się z dwóch kwadratów rzędu 3, jest podany poniżej.
Zamówienie 3
| 8 |
1 |
6
|
| 3 |
5 |
7
|
| 4 |
9 |
2
|
|
Zamów 3×3
| 63 |
63 |
63 |
0 |
0 |
0 |
45 |
45 |
45
|
| 63 |
63 |
63 |
0 |
0 |
0 |
45 |
45 |
45
|
| 63 |
63 |
63 |
0 |
0 |
0 |
45 |
45 |
45
|
| 18 |
18 |
18 |
36 |
36 |
36 |
54 |
54 |
54
|
| 18 |
18 |
18 |
36 |
36 |
36 |
54 |
54 |
54
|
| 18 |
18 |
18 |
36 |
36 |
36 |
54 |
54 |
54
|
| 27 |
27 |
27 |
72 |
72 |
72 |
9 |
9 |
9
|
| 27 |
27 |
27 |
72 |
72 |
72 |
9 |
9 |
9
|
| 27 |
27 |
27 |
72 |
72 |
72 |
9 |
9 |
9
|
|
Zamów 3×3
| 71 |
64 |
69 |
8 |
1 |
6 |
53 |
46 |
51
|
| 66 |
68 |
70 |
3 |
5 |
7 |
48 |
50 |
52
|
| 67 |
72 |
65 |
4 |
9 |
2 |
49 |
54 |
47
|
| 26 |
19 |
24 |
44 |
37 |
42 |
62 |
55 |
60
|
| 21 |
23 |
25 |
39 |
41 |
43 |
57 |
59 |
61
|
| 22 |
27 |
20 |
40 |
45 |
38 |
58 |
63 |
56
|
| 35 |
28 |
33 |
80 |
73 |
78 |
17 |
10 |
15
|
| 30 |
32 |
34 |
75 |
77 |
79 |
12 |
14 |
16
|
| 31 |
36 |
29 |
76 |
81 |
74 |
13 |
18 |
11
|
|
Ponieważ każdy z podkwadratów 3 × 3 może być niezależnie obracany i odbijany w 8 różnych kwadratach, z tego pojedynczego złożonego kwadratu 9 × 9 możemy wyprowadzić 8 9 = 134 217 728 zasadniczo różnych złożonych kwadratów 9 × 9. O wiele więcej złożonych magicznych kwadratów można również wyprowadzić, jeśli wybierzemy niekolejne liczby w magicznych podkwadratach, tak jak w wersji złożonego magicznego kwadratu 9×9 Yang Hui. Następne najmniejsze złożone magiczne kwadraty rzędu 12, złożone z magicznych kwadratów rzędu 3 i 4, są podane poniżej.
Zamówienie 3
| 2 |
9 |
4
|
| 7 |
5 |
3
|
| 6 |
1 |
8
|
|
Zamówienie 4
| 1 |
14 |
11 |
8
|
| 12 |
7 |
2 |
13
|
| 6 |
9 |
16 |
3
|
| 15 |
4 |
5 |
10
|
|
Zamów 3 × 4
| 2 |
9 |
4 |
119 |
126 |
121 |
92 |
99 |
94 |
65 |
72 |
67
|
| 7 |
5 |
3 |
124 |
122 |
120 |
97 |
95 |
93 |
70 |
68 |
66
|
| 6 |
1 |
8 |
123 |
118 |
125 |
96 |
91 |
98 |
69 |
64 |
71
|
| 101 |
108 |
103 |
56 |
63 |
58 |
11 |
18 |
13 |
110 |
117 |
112
|
| 106 |
104 |
102 |
61 |
59 |
57 |
16 |
14 |
12 |
115 |
113 |
111
|
| 105 |
100 |
107 |
60 |
55 |
62 |
15 |
10 |
17 |
114 |
109 |
116
|
| 47 |
54 |
49 |
74 |
81 |
76 |
137 |
144 |
139 |
20 |
27 |
22
|
| 52 |
50 |
48 |
79 |
77 |
75 |
142 |
140 |
138 |
25 |
23 |
21
|
| 51 |
46 |
53 |
78 |
73 |
80 |
141 |
136 |
143 |
24 |
19 |
26
|
| 128 |
135 |
130 |
29 |
36 |
31 |
38 |
45 |
40 |
83 |
90 |
85
|
| 133 |
131 |
129 |
34 |
32 |
30 |
43 |
41 |
39 |
88 |
86 |
84
|
| 132 |
127 |
134 |
33 |
28 |
35 |
42 |
37 |
44 |
87 |
82 |
89
|
|
Zamów 4 × 3
| 17 |
30 |
27 |
24 |
129 |
142 |
139 |
136 |
49 |
62 |
59 |
56
|
| 28 |
23 |
18 |
29 |
140 |
135 |
130 |
141 |
60 |
55 |
50 |
61
|
| 22 |
25 |
32 |
19 |
134 |
137 |
144 |
131 |
54 |
57 |
64 |
51
|
| 31 |
20 |
21 |
26 |
143 |
132 |
133 |
138 |
63 |
52 |
53 |
58
|
| 97 |
110 |
107 |
104 |
65 |
78 |
75 |
72 |
33 |
46 |
43 |
40
|
| 108 |
103 |
98 |
109 |
76 |
71 |
66 |
77 |
44 |
39 |
34 |
45
|
| 102 |
105 |
112 |
99 |
70 |
73 |
80 |
67 |
38 |
41 |
48 |
35
|
| 111 |
100 |
101 |
106 |
79 |
68 |
69 |
74 |
47 |
36 |
37 |
42
|
| 81 |
94 |
91 |
88 |
1 |
14 |
11 |
8 |
113 |
126 |
123 |
120
|
| 92 |
87 |
82 |
93 |
12 |
7 |
2 |
13 |
124 |
119 |
114 |
125
|
| 86 |
89 |
96 |
83 |
6 |
9 |
16 |
3 |
118 |
121 |
128 |
115
|
| 95 |
84 |
85 |
90 |
15 |
4 |
5 |
10 |
127 |
116 |
117 |
122
|
|
W przypadku kwadratów bazowych istnieje tylko jeden zasadniczo inny kwadrat trzeciego rzędu, podczas gdy istnieje 880 zasadniczo różnych kwadratów czwartego rzędu, z których możemy wybierać. Każda para może wytworzyć dwa różne kwadraty złożone. Ponieważ każdy magiczny podkwadrat w każdym złożonym kwadracie może być wyrażony w 8 różnych formach ze względu na rotacje i odbicia, może to być 1×880×8 9 + 880×1×8 16 ≈ 2,476×10 17 zasadniczo różne złożenie 12×12 utworzone w ten sposób magiczne kwadraty, z kolejnymi numerami w każdym podkwadracie. Ogólnie, jeśli jest to c m i c n zasadniczo różne magiczne kwadraty rzędu m i n , a następnie można formować c m x c n x (8 m 2 + 8 N 2 ) złożone kwadraty rzędu MN , pod warunkiem, m ≠ n . Jeśli m = n , to możemy utworzyć ( c m ) 2 × 8 m 2 złożone kwadraty rzędu m 2 .
W przypadku kwadratów o podwójnej kolejności
Kiedy kwadraty są podwójnie równej kolejności, możemy skonstruować złożony magiczny kwadrat w sposób bardziej elegancki niż powyższy proces, w tym sensie, że każdy magiczny podkwadrat będzie miał tę samą magiczną stałą. Niech n będzie rzędem kwadratu głównego, a m rzędem równych podkwadratów. Podkwadraty są wypełniane jeden po drugim, w dowolnej kolejności, ciągłym ciągiem m 2 /2 mniejszych liczb (tj. liczb mniejszych lub równych n 2 /2) wraz z ich uzupełnieniami do n 2 + 1. Każdy podkwadrat jako całość da taką samą magiczną sumę. Zaletą tego typu kwadratu złożonego jest to, że każdy podkwadrat jest wypełniany w ten sam sposób, a ich układ jest dowolny. Zatem znajomość pojedynczej konstrukcji parzystego porządku wystarczy, aby wypełnić cały kwadrat. Co więcej, jeśli podkwadraty są wypełnione w naturalnej kolejności, to wynikowy kwadrat będzie pandiagonalny. Magiczna suma podkwadratów jest powiązana z magiczną sumą całego kwadratu, gdzie n = km .

W poniższych przykładach podzieliliśmy kwadrat rzędu 12 na dziewięć podkwadratów rzędu 4 wypełnionych ośmioma mniejszymi liczbami, a w odpowiednich komórkach biskupa (dwie komórki po przekątnej, w tym zawijanie, w podkwadracie 4×4), ich uzupełnia n 2 + 1 = 145. Każdy podkwadrat jest pandiagonalny ze stałą magiczną 290; podczas gdy cały kwadrat po lewej jest również pandiagonalny ze stałą magiczną 870.
| 1 |
142 |
139 |
8 |
9 |
134 |
131 |
16 |
17 |
126 |
123 |
24
|
| 140 |
7 |
2 |
141 |
132 |
15 |
10 |
133 |
124 |
23 |
18 |
125
|
| 6 |
137 |
144 |
3 |
14 |
129 |
136 |
11 |
22 |
121 |
128 |
19
|
| 143 |
4 |
5 |
138 |
135 |
12 |
13 |
130 |
127 |
20 |
21 |
122
|
| 25 |
118 |
115 |
32 |
33 |
110 |
107 |
40 |
41 |
102 |
99 |
48
|
| 116 |
31 |
26 |
117 |
108 |
39 |
34 |
109 |
100 |
47 |
42 |
101
|
| 30 |
113 |
120 |
27 |
38 |
105 |
112 |
35 |
46 |
97 |
104 |
43
|
| 119 |
28 |
29 |
114 |
111 |
36 |
37 |
106 |
103 |
44 |
45 |
98
|
| 49 |
94 |
91 |
56 |
57 |
86 |
83 |
64 |
65 |
78 |
75 |
72
|
| 92 |
55 |
50 |
93 |
84 |
63 |
58 |
85 |
76 |
71 |
66 |
77
|
| 54 |
89 |
96 |
51 |
62 |
81 |
88 |
59 |
70 |
73 |
80 |
67
|
| 95 |
52 |
53 |
90 |
87 |
60 |
61 |
82 |
79 |
68 |
69 |
74
|
|
| 69 |
74 |
79 |
68 |
29 |
114 |
119 |
28 |
61 |
82 |
87 |
60
|
| 75 |
72 |
65 |
78 |
115 |
32 |
25 |
118 |
83 |
64 |
57 |
86
|
| 66 |
77 |
76 |
71 |
26 |
117 |
116 |
31 |
58 |
85 |
84 |
63
|
| 80 |
67 |
70 |
73 |
120 |
27 |
30 |
113 |
88 |
59 |
62 |
81
|
| 21 |
122 |
127 |
20 |
53 |
90 |
95 |
52 |
13 |
130 |
135 |
12
|
| 123 |
24 |
17 |
126 |
91 |
56 |
49 |
94 |
131 |
16 |
9 |
134
|
| 18 |
125 |
124 |
23 |
50 |
93 |
92 |
55 |
10 |
133 |
132 |
15
|
| 128 |
19 |
22 |
121 |
96 |
51 |
54 |
89 |
136 |
11 |
14 |
129
|
| 45 |
98 |
103 |
44 |
5 |
138 |
143 |
4 |
37 |
106 |
111 |
36
|
| 99 |
48 |
41 |
102 |
139 |
8 |
1 |
142 |
107 |
40 |
33 |
110
|
| 42 |
101 |
100 |
47 |
2 |
141 |
140 |
7 |
34 |
109 |
108 |
39
|
| 104 |
43 |
46 |
97 |
144 |
3 |
6 |
137 |
112 |
35 |
38 |
105
|
|
W innym przykładzie poniżej podzieliliśmy kwadraty rzędu 12 na cztery kwadraty rzędu 6. Każdy z sześciu kwadratów rzędu wypełniony jest osiemnastoma małymi cyframi i ich uzupełnieniami przy użyciu techniki obramowania podanej przez al-Antaki. Jeśli usuniemy zacienione granice podkwadratów rzędu 6 i utworzymy kwadrat rzędu 8, to ten kwadrat rzędu 8 jest znowu magicznym kwadratem. W pełnej ogólności możemy przyjąć dowolne m 2 /2 mniejsze liczby wraz z ich uzupełnieniami do n 2 + 1, aby wypełnić podkwadraty, niekoniecznie w sekwencji ciągłej.
| 60 |
82 |
88 |
56 |
90 |
59 |
24 |
118 |
124 |
20 |
126 |
23
|
| 64 |
69 |
74 |
79 |
68 |
81 |
28 |
33 |
110 |
115 |
32 |
117
|
| 83 |
75 |
72 |
65 |
78 |
62 |
119 |
111 |
36 |
29 |
114 |
26
|
| 84 |
66 |
77 |
76 |
71 |
61 |
120 |
30 |
113 |
112 |
35 |
25
|
| 58 |
80 |
67 |
70 |
73 |
87 |
22 |
116 |
31 |
34 |
109 |
123
|
| 86 |
63 |
57 |
89 |
55 |
85 |
122 |
27 |
21 |
125 |
19 |
121
|
| 6 |
136 |
142 |
2 |
144 |
5 |
42 |
100 |
106 |
38 |
108 |
41
|
| 10 |
15 |
128 |
133 |
14 |
135 |
46 |
51 |
92 |
97 |
50 |
99
|
| 137 |
129 |
18 |
11 |
132 |
8 |
101 |
93 |
54 |
47 |
96 |
44
|
| 138 |
12 |
131 |
130 |
17 |
7 |
102 |
48 |
95 |
94 |
53 |
43
|
| 4 |
134 |
13 |
16 |
127 |
141 |
40 |
98 |
49 |
52 |
91 |
105
|
| 140 |
9 |
3 |
143 |
1 |
139 |
104 |
45 |
39 |
107 |
37 |
103
|
Metoda Medjiga dla kwadratów parzystego rzędu 2 n , gdzie n > 2
W tej metodzie magiczny kwadrat jest "mnożony" przez kwadrat Medjig, aby stworzyć większy magiczny kwadrat. Imiennik tej metody wywodzi się z gry matematycznej o nazwie medjig stworzonej przez Willema Barinka w 2006 roku, choć sama metoda jest znacznie starsza. Wczesny przykład magicznego kwadratu skonstruowanego przy użyciu tej metody występuje w tekście Yang Hui dla magicznego kwadratu rzędu 6. Metoda LUX do konstruowania pojedynczych, nawet magicznych kwadratów jest szczególnym przypadkiem metody medjig, gdzie tylko 3 z 24 wzorów są używane do skonstruowania kwadratu medjig.
Kawałki łamigłówki to 2×2 kwadraty, na których umieszczone są cyfry 0, 1, 2 i 3. Istnieją trzy podstawowe wzory, według których liczby 0, 1, 2 i 3 można umieścić w kwadracie 2×2, gdzie 0 znajduje się w lewym górnym rogu:
Każdy wzór można odbijać i obracać, aby uzyskać 8 równoważnych wzorów, co daje w sumie 3×8 = 24 wzory. Celem łamigłówki jest zebranie n 2 kawałków medjigu i ułożenie ich w kwadracie n × n medjigu w taki sposób, aby każdy rząd, kolumna wraz z dwiema długimi przekątnymi utworzonymi przez kwadrat medjigu sumowały się do 3 n , magiczna stała kwadratu medjig. N × n medjig kwadrat może stworzyć 2 n x 2 n magiczny kwadrat, gdzie n > 2.
Mając n × n medjig kwadrat i n × n magiczny kwadrat o podstawie, magiczny kwadrat rzędu 2 n × 2 n może być skonstruowany w następujący sposób:
- Każda komórka magicznego kwadratu n × n jest powiązana z odpowiednim podkwadratem 2×2 kwadratu medjig
- Wypełnij każdy 2×2 podkwadrat kwadratu medjig czterema liczbami od 1 do 4 n 2, które są równe pierwotnej liczbie modulo n 2 , tj. x + n 2 y gdzie x jest odpowiednią liczbą z magicznego kwadratu, a y jest liczbą od 0 do 3 w podkwadratach 2×2.
Zakładając, że mamy początkową podstawę magicznego kwadratu, wyzwaniem jest skonstruowanie kwadratu Medjig. Dla porównania, sumy każdego kawałka medjigu wzdłuż rzędów, kolumn i przekątnych, oznaczone kursywą, są następujące:
Podwójnie parzyste kwadraty : Najmniejszy parzysty kwadrat medjig jest rzędu 2 ze stałą magiczną 6. Chociaż możliwe jest skonstruowanie kwadratu 2×2 medjig, nie możemy z niego skonstruować magicznego kwadratu 4×4 ponieważ wymagane są magiczne kwadraty 2×2 „pomnożyć” to nie istnieje. Niemniej jednak warto skonstruować te kwadraty 2×2 medjig. Magiczną stałą 6 można podzielić na dwie części na trzy sposoby: 6 = 5 + 1 = 4 + 2 = 3 + 3. Istnieje 96 takich kwadratów 2×2 medjig. W poniższych przykładach, każdy kwadrat 2×2 medjig jest tworzony przez połączenie różnych orientacji jednego kawałka medjigu.
Medjig 2×2
| 0 |
1 |
3 |
2
|
| 2 |
3 |
1 |
0
|
| 3 |
2 |
0 |
1
|
| 1 |
0 |
2 |
3
|
|
Medjig 2×2
| 0 |
1 |
2 |
3
|
| 3 |
2 |
1 |
0
|
| 1 |
0 |
3 |
2
|
| 2 |
3 |
0 |
1
|
|
Medjig 2×2
| 0 |
2 |
3 |
1
|
| 3 |
1 |
0 |
2
|
| 0 |
2 |
3 |
1
|
| 3 |
1 |
0 |
2
|
|
Możemy użyć kwadratów medjig 2×2 do budowy większych, nawet uporządkowanych kwadratów medjig. Jednym z możliwych podejść jest po prostu połączenie kwadratów 2×2 medjig razem. Inną możliwością jest owinięcie mniejszego kwadratowego rdzenia medjig ramką medjig. Kawałki kwadratu medjig 2×2 mogą tworzyć narożne fragmenty obramowania. Jeszcze inną możliwością jest dodanie wiersza i kolumny do nieparzystego uporządkowanego kwadratu medjig. Przykład magicznego kwadratu 8×8 jest skonstruowany poniżej, łącząc cztery kopie najbardziej od lewej kwadratu medjig 2×2 podanego powyżej:
Zamówienie 4
| 1 |
14 |
4 |
15
|
| 8 |
11 |
5 |
10
|
| 13 |
2 |
16 |
3
|
| 12 |
7 |
9 |
6
|
|
Medjig 4 × 4
| 0 |
1 |
3 |
2 |
0 |
1 |
3 |
2
|
| 2 |
3 |
1 |
0 |
2 |
3 |
1 |
0
|
| 3 |
2 |
0 |
1 |
3 |
2 |
0 |
1
|
| 1 |
0 |
2 |
3 |
1 |
0 |
2 |
3
|
| 0 |
1 |
3 |
2 |
0 |
1 |
3 |
2
|
| 2 |
3 |
1 |
0 |
2 |
3 |
1 |
0
|
| 3 |
2 |
0 |
1 |
3 |
2 |
0 |
1
|
| 1 |
0 |
2 |
3 |
1 |
0 |
2 |
3
|
|
Zamówienie 8
| 1 |
17 |
62 |
46 |
4 |
20 |
63 |
47
|
| 33 |
49 |
30 |
14 |
36 |
52 |
31 |
15
|
| 56 |
40 |
11 |
27 |
53 |
37 |
10 |
26
|
| 24 |
8 |
43 |
59 |
21 |
5 |
42 |
58
|
| 13 |
29 |
50 |
34 |
16 |
32 |
51 |
35
|
| 45 |
61 |
18 |
2 |
48 |
64 |
19 |
3
|
| 60 |
44 |
7 |
23 |
57 |
41 |
6 |
22
|
| 28 |
12 |
39 |
55 |
25 |
9 |
38 |
54
|
|
Następny przykład jest skonstruowany przez obramowanie kwadratowego rdzenia medjig 2×2.
Zamówienie 4
| 1 |
14 |
4 |
15
|
| 8 |
11 |
5 |
10
|
| 13 |
2 |
16 |
3
|
| 12 |
7 |
9 |
6
|
|
Medjig 4 × 4
| 0 |
1 |
0 |
1 |
2 |
3 |
3 |
2
|
| 2 |
3 |
3 |
2 |
1 |
0 |
1 |
0
|
| 0 |
3 |
0 |
2 |
3 |
1 |
0 |
3
|
| 1 |
2 |
3 |
1 |
0 |
2 |
1 |
2
|
| 2 |
1 |
0 |
2 |
3 |
1 |
2 |
1
|
| 3 |
0 |
3 |
1 |
0 |
2 |
3 |
0
|
| 3 |
2 |
0 |
1 |
2 |
3 |
0 |
1
|
| 1 |
0 |
3 |
2 |
1 |
0 |
2 |
3
|
|
Zamówienie 8
| 1 |
17 |
14 |
30 |
36 |
52 |
63 |
47
|
| 33 |
49 |
62 |
46 |
20 |
4 |
31 |
15
|
| 8 |
56 |
11 |
43 |
53 |
21 |
10 |
58
|
| 24 |
40 |
59 |
27 |
5 |
37 |
26 |
42
|
| 45 |
29 |
2 |
34 |
64 |
32 |
35 |
19
|
| 61 |
13 |
50 |
18 |
16 |
48 |
51 |
3
|
| 60 |
44 |
7 |
23 |
41 |
57 |
6 |
22
|
| 28 |
12 |
55 |
39 |
25 |
9 |
38 |
54
|
|
Pojedynczo równe kwadraty : kwadrat Medjig rzędu 1 nie istnieje. Jako taki, najmniejszy nieparzysty uporządkowany kwadrat medjig jest rzędu 3, ze stałą magiczną 9. Jest tylko 7 sposobów na podzielenie liczby całkowitej 9, naszej stałej magicznej, na trzy części. Jeśli te trzy części odpowiadają trzem elementom medjigu w rzędzie, kolumnie lub po przekątnej, to odpowiednie dla nas przegrody są
- 9 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 3 + 4 = 2 + 2 + 5 = 3 + 3 + 3.
Kwadrat medjig 3×3 można zbudować metodą prób i błędów, tak jak w kwadracie najbardziej po lewej poniżej. Innym podejściem jest dodanie wiersza i kolumny do kwadratu medjig 2×2. W środkowym kwadracie poniżej dodano lewą kolumnę i dolny rząd, tworząc ramkę medjig w kształcie litery L, do kwadratu medjig 2×2 podanego wcześniej. Kwadrat po prawej stronie poniżej jest zasadniczo taki sam jak kwadrat środkowy, z wyjątkiem tego, że rząd i kolumna zostały dodane pośrodku, aby utworzyć krzyż, podczas gdy kawałki kwadratu medjig 2×2 są umieszczone w rogach.
Medjig 3 × 3
| 2 |
3 |
0 |
2 |
0 |
2
|
| 1 |
0 |
3 |
1 |
3 |
1
|
| 3 |
1 |
1 |
2 |
2 |
0
|
| 0 |
2 |
0 |
3 |
3 |
1
|
| 3 |
2 |
2 |
0 |
0 |
2
|
| 0 |
1 |
3 |
1 |
1 |
3
|
|
Medjig 3 × 3
| 0 |
3 |
0 |
1 |
3 |
2
|
| 2 |
1 |
2 |
3 |
1 |
0
|
| 3 |
0 |
3 |
2 |
0 |
1
|
| 2 |
1 |
1 |
0 |
2 |
3
|
| 0 |
1 |
3 |
1 |
3 |
1
|
| 2 |
3 |
0 |
2 |
0 |
2
|
|
Medjig 3 × 3
| 0 |
1 |
0 |
3 |
3 |
2
|
| 2 |
3 |
2 |
1 |
1 |
0
|
| 3 |
1 |
0 |
1 |
3 |
1
|
| 0 |
2 |
2 |
3 |
0 |
2
|
| 3 |
2 |
3 |
0 |
0 |
1
|
| 1 |
0 |
2 |
1 |
2 |
3
|
|
Po skonstruowaniu kwadratu medjigu 3×3, możemy przekształcić go w magiczny kwadrat 6×6. Na przykład, używając kwadratu medjig 3×3 najbardziej od lewej podanego powyżej:
Zamówienie 3
| 8 |
1 |
6
|
| 3 |
5 |
7
|
| 4 |
9 |
2
|
|
Medjig 3 × 3
| 2 |
3 |
0 |
2 |
0 |
2
|
| 1 |
0 |
3 |
1 |
3 |
1
|
| 3 |
1 |
1 |
2 |
2 |
0
|
| 0 |
2 |
0 |
3 |
3 |
1
|
| 3 |
2 |
2 |
0 |
0 |
2
|
| 0 |
1 |
3 |
1 |
1 |
3
|
|
Zamówienie 6
| 26 |
35 |
1 |
19 |
6 |
24
|
| 17 |
8 |
28 |
10 |
33 |
15
|
| 30 |
12 |
14 |
23 |
25 |
7
|
| 3 |
21 |
5 |
32 |
34 |
16
|
| 31 |
22 |
27 |
9 |
2 |
20
|
| 4 |
13 |
36 |
18 |
11 |
29
|
|
Takich kwadratów medjigowych 3×3 jest 1 740 800. Łatwym podejściem do skonstruowania nieparzystego kwadratu medjig wyższego rzędu jest owinięcie mniejszego nieparzystego ułożonego kwadratu medjig ramką medjig, tak jak w przypadku parzystych kwadratów medjig. Innym podejściem jest dołączenie wiersza i kolumny do parzystego kwadratu medjig. Można również zastosować takie podejścia, jak metoda LUX. W poniższym przykładzie kwadrat medjig 5×5 jest tworzony przez zawinięcie ramki medjig wokół kwadratu medjig 3×3 podanego wcześniej:
Zamów 5
| 17 |
24 |
1 |
8 |
15
|
| 23 |
5 |
7 |
14 |
16
|
| 4 |
6 |
13 |
20 |
22
|
| 10 |
12 |
19 |
21 |
3
|
| 11 |
18 |
25 |
2 |
9
|
|
Medjig 5 × 5
| 0 |
1 |
3 |
1 |
0 |
1 |
3 |
1 |
3 |
2
|
| 2 |
3 |
0 |
2 |
2 |
3 |
0 |
2 |
1 |
0
|
| 3 |
0 |
2 |
3 |
0 |
2 |
0 |
2 |
1 |
2
|
| 1 |
2 |
1 |
0 |
3 |
1 |
3 |
1 |
3 |
0
|
| 0 |
2 |
3 |
1 |
1 |
2 |
2 |
0 |
1 |
3
|
| 1 |
3 |
0 |
2 |
0 |
3 |
3 |
1 |
0 |
2
|
| 3 |
0 |
3 |
2 |
2 |
0 |
0 |
2 |
1 |
2
|
| 1 |
2 |
0 |
1 |
3 |
1 |
1 |
3 |
3 |
0
|
| 3 |
2 |
1 |
3 |
1 |
0 |
1 |
3 |
0 |
1
|
| 1 |
0 |
2 |
0 |
3 |
2 |
2 |
0 |
2 |
3
|
|
Zamów 10
| 17 |
42 |
99 |
49 |
1 |
26 |
83 |
33 |
90 |
65
|
| 67 |
92 |
24 |
74 |
51 |
76 |
8 |
58 |
40 |
15
|
| 98 |
23 |
55 |
80 |
7 |
57 |
14 |
64 |
41 |
66
|
| 48 |
73 |
30 |
5 |
82 |
32 |
89 |
39 |
91 |
16
|
| 4 |
54 |
81 |
31 |
38 |
63 |
70 |
20 |
47 |
97
|
| 29 |
79 |
6 |
56 |
13 |
88 |
95 |
45 |
22 |
72
|
| 85 |
10 |
87 |
62 |
69 |
19 |
21 |
71 |
28 |
53
|
| 35 |
60 |
12 |
37 |
94 |
44 |
46 |
96 |
78 |
3
|
| 86 |
61 |
43 |
93 |
100 |
25 |
27 |
77 |
9 |
34
|
| 36 |
11 |
68 |
18 |
95 |
75 |
52 |
2 |
59 |
84
|
|
Rozwiązywanie częściowo ukończonych magicznych kwadratów
Rozwiązywanie częściowo ukończonych magicznych kwadratów jest popularną rozrywką matematyczną. Potrzebne techniki są podobne do tych stosowanych w łamigłówkach Sudoku lub KenKen i polegają na wydedukowaniu wartości niewypełnionych kwadratów za pomocą logiki i teorii grup permutacji (siatki Sudoku nie są magicznymi kwadratami, ale opierają się na podobnej idei zwanej kwadratami grecko-łacińskimi ).
Wariacje magicznego kwadratu

Magiczny kwadrat Ramanujana
Na magiczne kwadraty mogą zostać nałożone pewne dodatkowe ograniczenia.
Jeśli podniesienie każdej liczby do n- tej potęgi daje kolejny magiczny kwadrat, wynikiem jest bimagia (n = 2), trymagia (n = 3) lub ogólnie multimagiczny kwadrat .
Magiczny kwadrat, w którym liczba liter w nazwie każdej liczby w kwadracie generuje kolejny magiczny kwadrat, nazywa się kwadratem alfamagicznym .
Istnieją magiczne kwadraty składające się wyłącznie z liczb pierwszych . Rudolf Ondrejka (1928–2001) odkrył następujący magiczny kwadrat liczb pierwszych 3×3 , w tym przypadku dziewięć liczb pierwszych Chen :
| 17 |
89 |
71
|
| 113 |
59 |
5
|
| 47 |
29 |
101
|
Twierdzenie Greena-Tao sugeruje, że istnieją dowolnie duże magiczne kwadraty składające się z liczb pierwszych.
Poniższy „odwracalny magiczny kwadrat” ma magiczną stałą 264 zarówno do góry nogami, jak i do góry nogami:
| 96 |
11 |
89 |
68
|
| 88 |
69 |
91 |
16
|
| 61 |
86 |
18 |
99
|
| 19 |
98 |
66 |
81
|
Gdy dodatkowym ograniczeniem jest wyświetlanie jakiejś daty, zwłaszcza daty urodzenia, wtedy takie magiczne kwadraty nazywane są magicznym kwadratem urodzin. Wczesny przykład takiego urodzinowego magicznego kwadratu został stworzony przez Srinivasę Ramanujan . Stworzył kwadrat 4×4, w którym w górnym wierszu wpisał swoją datę urodzenia w formacie DD-MM-CC-RR, a magia wydarzyła się z dodawaniem i odejmowaniem liczb w kwadratach. Nie tylko rzędy, kolumny i przekątne sumują się do tej samej liczby, ale cztery rogi, cztery środkowe kwadraty (17, 9, 24, 89), pierwszy i ostatni wiersz dwie środkowe liczby (12, 18, 86 , 23) oraz w pierwszej i ostatniej kolumnie dwie środkowe liczby (88, 10, 25, 16) sumują się do sumy 139.
Mnożenie magicznych kwadratów
Zamiast dodawać liczby w każdym rzędzie, kolumnie i przekątnej, można zastosować inną operację. Na przykład multiplikatywny kwadrat magiczny ma stały iloczyn liczb. Mnożnikowy kwadrat magiczny można wyprowadzić z addytywnego kwadratu magicznego, podnosząc 2 (lub dowolną inną liczbę całkowitą) do potęgi każdego elementu, ponieważ logarytm iloczynu 2 liczb jest sumą logarytmów każdej z nich. Alternatywnie, jeśli dowolne 3 liczby w wierszu to 2 a , 2 b i 2 c , ich iloczynem jest 2 a + b + c , co jest stałe, jeśli a + b + c jest stałe, tak jak byłoby, gdyby a , b i c zostały zaczerpnięte ze zwykłego (dodatkowego) magicznego kwadratu. Na przykład oryginalny magiczny kwadrat Lo-Shu staje się:
M = 32768
| 16 |
512 |
4
|
| 8 |
32 |
128
|
| 256 |
2 |
64
|
Inne przykłady multiplikatywnych magicznych kwadratów obejmują:
M = 216
| 2 |
9 |
12
|
| 36 |
6 |
1
|
| 3 |
4 |
18
|
|
M = 6720
| 1 |
6 |
20 |
56
|
| 40 |
28 |
2 |
3
|
| 14 |
5 |
24 |
4
|
| 12 |
8 |
7 |
10
|
|
M = 6 227 020 800
| 27 |
50 |
66 |
84 |
13 |
2 |
32
|
| 24 |
52 |
3 |
40 |
54 |
70 |
11
|
| 56 |
9 |
20 |
44 |
36 |
65 |
6
|
| 55 |
72 |
91 |
1 |
16 |
36 |
30
|
| 4 |
24 |
45 |
60 |
77 |
12 |
26
|
| 10 |
22 |
48 |
39 |
5 |
48 |
63
|
| 78 |
7 |
8 |
18 |
40 |
33 |
60
|
|
Mnożenie magicznych kwadratów liczb zespolonych
Wciąż stosując nieiteracyjną metodę Ali Skalli , możliwe jest wytworzenie nieskończoności multiplikatywnych kwadratów magicznych liczb zespolonych należących do zbioru. W poniższym przykładzie części rzeczywiste i urojone są liczbami całkowitymi, ale mogą również należeć do całego zbioru liczb rzeczywistych . Produkt to: −352.507.340.640 − 400.599.719.520 i .


Skalli multiplikatyw 7×7 liczb zespolonych
| 21 |
+14 ja
|
−70 |
+30 ja
|
−93 |
-9 i
|
−105 |
-217 i
|
16 |
+50 ja
|
4 |
-14 i
|
14 |
-8 i
|
| 63 |
-35 i
|
28 |
+114 i
|
|
-14 i
|
2 |
+6 ja
|
3 |
-11 i
|
211 |
+357 ja
|
−123 |
-87 i
|
| 31 |
-15 i
|
13 |
-13 i
|
-103 |
+69 ja
|
-261 |
-213 i
|
49 |
−49 i
|
−46 |
+2 i
|
-6 |
+2 i
|
| 102 |
−84 i
|
−28 |
-14 i
|
43 |
+247 i
|
-10 |
-2 i
|
5 |
+9 i
|
31 |
−27 i
|
−77 |
+91 ja
|
| −22 |
-6 i
|
7 |
+7 ja
|
8 |
+14 ja
|
50 |
+20 ja
|
-525 |
-492 i
|
−28 |
−42 i
|
−73 |
+17 ja
|
| 54 |
+68 ja
|
138 |
-165 i
|
−56 |
-98 i
|
−63 |
+35 ja
|
4 |
-8 i
|
2 |
-4 i
|
70 |
-53 ja
|
| 24 |
+22 ja
|
−46 |
-16 i
|
6 |
-4 i
|
17 |
+20 ja
|
110 |
+160 i
|
84 |
−189 i
|
42 |
-14 i
|
Magia addytywno-multiplikatywna i półmagiczne kwadraty
Addytywno-multiplikatywne magiczne kwadraty i półmagiczne kwadraty spełniają odpowiednio właściwości zarówno zwykłych, jak i multiplikatywnych magicznych kwadratów i półmagicznych kwadratów.
Pierwszy znany
addytywno-multiplikatywny magiczny kwadrat
8×8 znaleziony przez WW Hornera w 1955 r.
Suma = 840
Produkt =2 058 068 231 856 000
| 162 |
207 |
51 |
26 |
133 |
120 |
116 |
25
|
| 105 |
152 |
100 |
29 |
138 |
243 |
39 |
34
|
| 92 |
27 |
91 |
136 |
45 |
38 |
150 |
261
|
| 57 |
30 |
174 |
225 |
108 |
23 |
119 |
104
|
| 58 |
75 |
171 |
90 |
17 |
52 |
216 |
161
|
| 13 |
68 |
184 |
189 |
50 |
87 |
135 |
114
|
| 200 |
203 |
15 |
76 |
117 |
102 |
46 |
81
|
| 153 |
78 |
54 |
69 |
232 |
175 |
19 |
60
|
|
Najmniejszy znany addytywno-multiplikatywny półmagiczny kwadrat
4×4 znaleziony przez L. Morgensterna w 2007 r.
Suma = 247
Produkt =3 369 600
| 156 |
18 |
48 |
25
|
| 30 |
144 |
60 |
13
|
| 16 |
20 |
130 |
81
|
| 45 |
65 |
9 |
128
|
|
Nie wiadomo, czy istnieją jakieś addytywno-multiplikatywne magiczne kwadraty mniejsze niż 8×8, ale udowodniono, że nie istnieją 3×3 lub 4×4 addytywno-multiplikatywne magiczne kwadraty ani 3×3 addytywno-multiplikatywne półmagiczne kwadraty.
Geometryczne magiczne kwadraty

Geometryczny magiczny kwadrat.
Można konstruować magiczne kwadraty, które zamiast liczb zawierają kształty geometryczne. Takie kwadraty, znane jako geometryczne kwadraty magiczne , zostały wymyślone i nazwane przez Lee Sallowsa w 2001 roku.
W pokazanym przykładzie pojawiające się kształty są dwuwymiarowe. Było to odkrycie Sallowsa, że wszystkie magiczne kwadraty są geometryczne, liczby pojawiające się w numerycznych magicznych kwadratach można interpretować jako zapis skrócony, który wskazuje długości odcinków linii prostych, które są geometrycznymi „kształtami” występującymi w kwadracie. Oznacza to, że numeryczne kwadraty magiczne są szczególnym przypadkiem geometrycznego kwadratu magicznego wykorzystującego jednowymiarowe kształty.
Obszar magiczne kwadraty

Pierwszy magiczny kwadrat obszaru liniowego
W 2017 roku, zgodnie z początkowymi pomysłami Williama Walkingtona i Inder Taneja , Walter Trump zbudował pierwszy magiczny kwadrat liniowy (L-AMS) .
Inne magiczne kształty
Można rozważyć inne kształty dwuwymiarowe niż kwadraty. Ogólnym przypadkiem jest uznanie projektu z N częściami za magiczny, jeśli N części jest oznaczonych numerami od 1 do N, a liczba identycznych podprojektów daje taką samą sumę. Przykłady obejmują magiczne kręgi , magiczne prostokąty, magiczne trójkąty, magiczne gwiazdy , magiczne sześciokąty , magiczne diamenty. Przechodzenie w górę skutkuje magicznymi kulami, magicznymi cylindrami, magicznymi sześcianami , magicznymi równoległościanami, magicznymi bryłami i innymi magicznymi hipersześcianami .
Możliwe magiczne kształty są ograniczone liczbą jednakowych podzbiorów o równej sumie wybranego zestawu etykiet. Na przykład, jeśli ktoś proponuje stworzyć magiczny kształt oznaczający części za pomocą {1, 2, 3, 4}, podprojekty będą musiały być oznaczone za pomocą {1,4} i {2,3}.
Powiązane problemy
n - Problem z hetmanami
W 1992 roku Demirörs, Rafraf i Tanik opublikowali metodę zamiany niektórych magicznych kwadratów na rozwiązania n- królowych i vice versa.
Magiczne kwadraty w okultyzmie
Magiczne kwadraty rzędu od 3 do 9, przypisane do siedmiu planet i opisane jako środki przyciągające wpływ planet i ich aniołów (lub demonów) podczas praktyk magicznych, można znaleźć w kilku rękopisach w całej Europie, począwszy od co najmniej od XV w. stulecie. Wśród najbardziej znanych, Liber de Angelis , magiczny podręcznik napisany około 1440 roku, znajduje się w Cambridge Univ. Lib. MS Dd.xi.45. Tekst Liber de Angelis jest bardzo zbliżony do tekstu De septem quadraturis planetarum seu quadrati magici , kolejnego podręcznika magii obrazów planet, zawartego w Kodeksie 793 Biblioteki Jagiellońskiej (Pani BJ 793). Magiczne operacje polegają na wygrawerowaniu odpowiedniego kwadratu na talerzu wykonanym z metalu przypisanego do odpowiedniej planety, a także odprawieniu różnorodnych rytuałów. Na przykład kwadrat 3×3 należący do Saturna musi być wypisany na ołowianej płytce. W szczególności pomoże kobietom podczas trudnego porodu.
Około 1510 roku Heinrich Cornelius Agryppa napisał De Occulta Philosophia , czerpiąc z hermetycznych i magicznych dzieł Marsilio Ficino i Pico della Mirandola . W wydaniu z 1531 r. objaśnił magiczne zalety siedmiu magicznych kwadratów o rzędach od 3 do 9, z których każdy związany jest z jedną z planet astrologicznych , podobnie jak czyniły to starsze teksty. Książka ta była bardzo wpływowa w całej Europie, aż do czasu kontrreformacji , a magiczne kwadraty Agryppy, czasami nazywane kameas, nadal są używane we współczesnej magii ceremonialnej w taki sam sposób, w jaki pierwotnie przepisał.
Najczęstszym zastosowaniem tych kameas jest dostarczenie wzoru, na podstawie którego można zbudować sigile duchów, aniołów lub demonów ; litery nazwy istoty są zamieniane na liczby, a linie są śledzone przez wzór, który te kolejne liczby tworzą na kamei. W kontekście magicznym, termin magiczny kwadrat jest również stosowany do różnych kwadratów słownych lub kwadratów liczbowych występujących w magicznych grimuarach , w tym takich, które nie mają żadnego oczywistego wzoru, a nawet tych z różną liczbą rzędów i kolumn. Są one na ogół przeznaczone do użytku jako talizmany. Na przykład następujące kwadraty to: Kwadrat Sator , jeden z najbardziej znanych magicznych kwadratów znalezionych w wielu grimuarach, w tym w Kluczu Salomona ; kwadrat „do przezwyciężenia zawiści”, z Księgi Mocy ; oraz dwa kwadraty z Księgi Świętej Magii Maga Abramelina , pierwszy wywołujący iluzję wspaniałego pałacu, drugi noszony na głowie dziecka podczas anielskiej inwokacji :
| S |
A |
T |
O |
r
|
| A |
r |
mi |
P |
O
|
| T |
mi |
n |
mi |
T
|
| O |
P |
mi |
r |
A
|
| r |
O |
T |
A |
S
|
|
| 6 |
66 |
848 |
938
|
| 8 |
11 |
544 |
839
|
| 1 |
11 |
383 |
839
|
| 2 |
73 |
774 |
447
|
|
| h |
mi |
S |
mi |
b
|
| mi |
Q |
A |
L |
|
| S |
|
|
|
|
| mi |
|
g |
|
|
| b |
|
|
|
|
|
| A |
D |
A |
m
|
| D |
A |
r |
A
|
| A |
r |
A |
D
|
| m |
A |
D |
A
|
|
Magiczne kwadraty w kulturze popularnej

Znaczki Makau z magicznymi kwadratami
- W Fauście Goethego zaklęcie wiedźmy użyte do zrobienia eliksiru młodości dla Fausta, Hexen-Einmal-Eins [ de ] , zostało zinterpretowane jako konstrukcja magicznego kwadratu.
- Angielski kompozytor Peter Maxwell Davies użył magicznych kwadratów do budowy wielu swoich kompozycji. Na przykład jego Ave Maris Stella z 1975 roku używa magicznego kwadratu Księżyca 9×9, podczas gdy jego Lustro wybielającego światła z 1977 roku używa magicznego kwadratu Merkurego 8×8 do stworzenia całego zestawu nut i czasu trwania utworu. Inne jego dzieła, w których zastosowano magiczne kwadraty, to Latarnia morska (1979), Zmartwychwstanie (1987), III Koncert Strathclyde na róg i trąbkę (1989), a także wiele jego symfonii. Według własnej relacji Daviesa:
Magiczny kwadrat w kompozycji muzycznej nie jest blokiem liczb – jest to zasada generująca, której należy się nauczyć i poznać wewnętrznie, postrzegana wewnętrznie jako wielowymiarowa projekcja w ten rozległy (chaotyczny!) obszar ucha wewnętrznego – przestrzeń /tygiel czasu – gdzie powstaje muzyka. ...Wyświetlany na stronie magiczny kwadrat jest martwą, czarną konglomeratem cyfr; dostroić się i usłyszeć potężne, orbitujące dynamo muzycznych obrazów, jarzące się numenami i lumenami.
- Magiczne kwadraty, w tym te Benjamina Franklina , pojawiają się jako wskazówki do zagadki w powieściach Katherine Neville „ Osiem i ogień” .
- Magiczny kwadrat Dürera i jego Melencolia I odegrały również duże role w powieści Dana Browna z 2009 roku, The Lost Symbol .
- W 2011 koreańskiego dramatu telewizyjnego mocno zakorzenione drzewo , Król Sejong jest pokazany próbując skonstruować kwadrat 33 x 33 przy użyciu magicznego pudełka na kanapki. Ostatecznie odkrywa „metodę piramidy” i uzupełnia magiczny kwadrat z pomocą armii dworskich. To inspiruje go do stworzenia bardziej sprawiedliwej formy rządu rządzonej rozumem i słowami, a nie potęgą militarną.
- 9 października 2014 r. urząd pocztowy Makau w Chińskiej Republice Ludowej wydał serię znaczków opartych na magicznych kwadratach. Poniższy rysunek przedstawia znaczki z dziewięcioma magicznymi kwadratami wybranymi do tej kolekcji.
- Metalowy artefakt w centrum odcinka „ Biogeneza ” z Archiwum X jest uważany przez Chucka Burksa za magiczny kwadrat.
- Matematyk Matt Parker próbował stworzyć magiczny kwadrat 3×3 za pomocą liczb kwadratowych w filmie YouTube na kanale Numberphile . Jego nieudana próba jest znana jako Parker Square .
- Pierwszy sezon Stargate Atlantis odcinek „Brotherhood” polega na ukończeniu magicznego kwadratu jako części układanki strzegącej potężnego starożytnego artefaktu.
- Magiczne kwadraty pojawiły się również w hiszpańskim filmie Vivir dos veces z 2019 roku .
Zobacz też
Uwagi
Bibliografia
- John Lee Fults, Magiczne kwadraty . (La Salle, Illinois: Sąd Otwarty, 1974).
-
Cliff Pickover , Zen magicznych kwadratów, kół i gwiazd (Princeton, New Jersey: Princeton University Press)
- Leonhard Euler, O magicznych kwadratach
- Leonhard Euler, Badania nowego typu magicznego kwadratu
-
William H. Benson i Oswald Jacoby , „Nowe rekreacje z magicznymi kwadratami”. (Nowy Jork: Dover, 1976).
Dalsza lektura
Zewnętrzne linki

































![{\ Displaystyle M = na + {\ Frac {n} {2}} {\ duży [} (r-1) c + (s-1) d {\ duży]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1315a1e80e660caa150524368fc718884b56906e)








