Rozkład drzewa - Tree decomposition

Wykres z ośmioma wierzchołkami i dekompozycja drzewa na drzewo z sześcioma węzłami. Każda krawędź grafu łączy dwa wierzchołki, które są wymienione razem w jakimś węźle drzewa, a każdy wierzchołek grafu jest wymieniony w węzłach sąsiedniego poddrzewa drzewa. Każdy węzeł drzewa zawiera co najwyżej trzy wierzchołki, więc szerokość tej dekompozycji wynosi dwa.

W teorii wykres , A rozkładu drzewa jest odwzorowaniem z wykresu na drzewie , które mogą być wykorzystane do określenia treewidth wykresu i przyspieszyć rozwiązanie pewnych problemów obliczeniowych na wykresie.

Rozkłady drzewo nazywane są również drzewa połączeniowe , klika drzew lub dołączyć drzew ; odgrywają one ważną rolę w problemach takich jak probabilistycznego wnioskowania , więzów satysfakcji , optymalizacji zapytań i rozkład macierzy .

Pojęcie rozkładu drzew zostało pierwotnie wprowadzone przez Rudolfa Halina  ( 1976 ). Później została ponownie odkryta przez Neila Robertsona i Paula Seymoura  ( 1984 ) i od tego czasu była badana przez wielu innych autorów.

Definicja

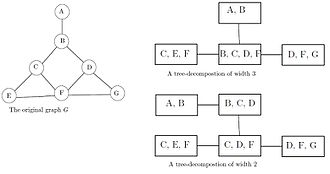
Intuicyjnie dekompozycja drzewa przedstawia wierzchołki danego grafu G jako poddrzewa drzewa, w taki sposób, że wierzchołki w danym grafie sąsiadują ze sobą tylko wtedy, gdy przecinają się odpowiadające im poddrzewa. A zatem, G tworzy podgrafu na wykresie przecięcia z poddrzewach. Pełny wykres przecięcia jest wykresem akordowym .

Każde poddrzewo wiąże wierzchołek grafu z zestawem węzłów drzewa. Aby zdefiniować to formalnie, reprezentujemy każdy węzeł drzewa jako zbiór wierzchołków z nim związanych. Zatem przy danym grafie G = ( V , E ) rozkład drzewa jest parą ( X , T ), gdzie X = { X ₁ , ..., X _n } jest rodziną podzbiorów (czasami nazywanych workami ) V i T to drzewo, którego węzły są podzbiorami X _i , spełniające następujące właściwości:

1. Suma wszystkich zbiorów X _i równa się V . Oznacza to, że każdy wierzchołek grafu jest powiązany z co najmniej jednym węzłem drzewa.
2. Dla każdej krawędzi ( v , w ) na wykresie istnieje podzbiór X _i zawierający zarówno v , jak i w . Oznacza to, że wierzchołki na wykresie sąsiadują ze sobą tylko wtedy, gdy odpowiadające im poddrzewa mają wspólny węzeł.
3. Jeśli X _i i X _j zawierają wierzchołek v , to wszystkie węzły X _k drzewa w (unikalnej) ścieżce między X _i i X _{j również} zawierają v . Oznacza to, że węzły skojarzone z wierzchołkiem v tworzą połączony podzbiór T . Jest to również znane jako koherencja lub biegnąca właściwość przecięcia . Można stwierdzić, że jeżeli równoważnie , a są węzły, i znajduje się na ścieżce od do , a następnie .${\ Displaystyle X_ {i}}$${\ Displaystyle X_ {j}}$${\ Displaystyle X_ {k}}$${\ Displaystyle X_ {k}}$${\ Displaystyle X_ {i}}$${\ Displaystyle X_ {j}}$${\ Displaystyle X_ {i} \ czapka X_ {j} \ subseteq X_ {k}}$

Rozkład drzewa grafu nie jest wyjątkowy; na przykład trywialna dekompozycja drzewa zawiera wszystkie wierzchołki grafu w swoim pojedynczym węźle korzeniowym.

Dekompozycja drzewa, w której drzewo bazowe jest wykresem ścieżki, nazywana jest dekompozycją ścieżki, a parametr szerokości pochodzący z tych specjalnych typów dekompozycji drzewa jest znany jako pathwidth .

Rozkład drzewa ( X , T = ( I , F )) szerokości drzewa k jest gładki , jeśli dla wszystkich i dla wszystkich . ${\ Displaystyle i \ w I: | X_ {i} | = k + 1}$${\ Displaystyle (i, j) \ w F: | X_ {i} \ czapka X_ {j} | = k}$

Minimalna liczba drzew w rozkładzie drzewa jest numer drzewo z G.

Szerokość drzewa

Dwie różne dekompozycje drzew tego samego grafu

Szerokość od rozkładu drzewa jest rozmiar największego zadanej X _I minus jeden. Treewidth tw ( G ) grafu G jest minimalna szerokość spośród wszystkich możliwych dekompozycji drzewa o G . W tej definicji rozmiar największego zbioru zmniejsza się o jeden, aby szerokość drzewa była równa jeden. Szerokość drzewa może być również zdefiniowana z innych struktur niż dekompozycje drzew, w tym grafów akordowych , jeżyn i przystani .

Jest NP-zupełne określenie, czy dany graf G ma szerokość drzewa co najwyżej dla danej zmiennej k . Jednak, gdy k jest dowolną stałą stała, wykresy z treewidth k mogą być uznane, a szerokość k rozkładu drzewo zbudowane dla nich, w czasie liniowym. Zależność czasowa tego algorytmu od k jest wykładnicza.

Programowanie dynamiczne

Na początku lat 70. zaobserwowano, że duża klasa problemów optymalizacji kombinatorycznej zdefiniowanych na grafach może być skutecznie rozwiązywana przez nieszeregowe programowanie dynamiczne, o ile graf ma wymiar ograniczony , parametr związany z szerokością drzewa. Później kilku autorów niezależnie zaobserwowało, pod koniec lat osiemdziesiątych, że wiele problemów algorytmicznych, które są NP-zupełne dla dowolnych grafów, można skutecznie rozwiązać za pomocą programowania dynamicznego dla grafów o ograniczonej szerokości drzewa, przy użyciu drzewiastej dekompozycji tych grafów.

Jako przykład rozważmy problem znalezienia maksymalnego niezależnego zbioru na grafie szerokości drzewa k . Aby rozwiązać ten problem, najpierw wybierz arbitralnie jeden z węzłów rozkładu drzewa jako korzeń. Dla węzła X _i rozkładu drzewa niech D _i będzie sumą zbiorów X _j malejąco od X _i . W przypadku niezależnego zbioru S  ⊂  X _i niech ( S , I ) oznaczają wielkości największego niezależnego podgrupy I z D _i tak że ja  ∩  X _i  =  S . Podobnie dla sąsiedniej pary węzłów X _i i X _j , gdzie X _{i znajduje się} dalej od korzenia drzewa niż X _j , i dla zbioru niezależnego S  ⊂  X _i  ∩  X _j , niech B ( S , i , j ) oznacza rozmiar największego niezależnego podzbioru I z D _i taki, że I  ∩  X _i  ∩  X _j  =  S . Możemy obliczyć te wartości A i B przez przechodzenie drzewa od dołu do góry:

${\ Displaystyle A (S, i) = | S | + \ suma _ {j} \ lewo (B (S \ czapka X_ {j}, j, i) - | S \ czapka X_ {j} | \ prawej) }$

${\ Displaystyle B (S, i, j) = \ max _ {S '\ podzbiór X_ {i} \ atop S = S '\ czapka X_ {j}} A (S', i)}$

gdzie suma w obliczeniach jest nad dziećmi węzła . ${\displaystyle A(S,i)}$${\ Displaystyle X_ {i}}$

W każdym węźle lub krawędzi są co najwyżej 2 ^k zbiorów S, dla których musimy obliczyć te wartości, więc jeśli k jest stałą, to całe obliczenie zajmuje stały czas na krawędź lub węzeł. Rozmiar maksymalnego niezależnego zestawu jest największą wartością przechowywaną w węźle głównym, a sam maksymalny niezależny zestaw można znaleźć (co jest standardem w algorytmach programowania dynamicznego) przez cofanie się przez te przechowywane wartości, zaczynając od tej największej wartości. Zatem w grafach o ograniczonej szerokości drzewa problem maksymalnego niezależnego zbioru można rozwiązać w czasie liniowym. Podobne algorytmy mają zastosowanie do wielu innych problemów grafowych.

To dynamiczne podejście do programowania jest wykorzystywane w uczeniu maszynowym za pomocą algorytmu drzewa połączeń do propagacji przekonań w grafach o ograniczonej szerokości drzewa. Odgrywa również kluczową rolę w algorytmach obliczania szerokości drzewa i konstruowania dekompozycji drzewa: zazwyczaj takie algorytmy mają pierwszy krok, który przybliża szerokość drzewa, konstruowanie dekompozycji drzewa o tej przybliżonej szerokości, a następnie drugi krok, który wykonuje dynamiczne programowanie w przybliżony rozkład drzewa w celu obliczenia dokładnej wartości szerokości drzewa.

Zobacz też

• Brambles and havens  — dwa rodzaje struktur, których można użyć jako alternatywy dla dekompozycji drzewa podczas definiowania szerokości drzewa grafu.
• Rozkład gałęzi  — ściśle powiązana struktura, której szerokość mieści się w stałym współczynniku szerokości drzewa.
• Metoda dekompozycji  – Dekompozycja drzewa jest wykorzystywana w Metodzie dekompozycji do rozwiązywania problemu spełniania ograniczeń.

Uwagi

Bibliografia