Siły statyczne i wirtualna wymiana cząstek - Static forces and virtual-particle exchange

Pola sił statycznych to pola, takie jak proste pola elektryczne , magnetyczne lub grawitacyjne , które istnieją bez wzbudzeń. Najbardziej powszechną metodą przybliżenie że fizyków użyć do rozpraszania obliczeń może być interpretowany jako siły statyczne wynikające z interakcji między dwoma korpusami w których pośredniczy wirtualnych cząstek , cząstek, które występują tylko na krótki okres czasu określony przez zasady niepewności . Wirtualne cząstki, znane również jako nośniki siły , to bozony , z różnymi bozonami związanymi z każdą siłą.

Opis wirtualnych cząstek sił statycznych jest w stanie zidentyfikować przestrzenną formę sił, taką jak zachowanie odwrotnego kwadratu w prawie powszechnego ciążenia Newtona i prawie Coulomba . Jest również w stanie przewidzieć, czy siły są przyciągające, czy odpychające dla podobnych ciał.

Sformułowanie integralną ścieżka jest językiem naturalnym opisujący nośniki siły. W tym artykule wykorzystano formułę całki po ścieżce do opisania nośników siły dla pól spinu 0, 1 i 2. Piony , fotony i grawitony należą do tych odpowiednich kategorii.

Wiarygodność obrazu cząstek wirtualnych jest ograniczona. Sformułowanie cząstek wirtualnych wywodzi się z metody znanej jako teoria zaburzeń, która jest przybliżeniem zakładającym, że oddziaływania nie są zbyt silne i była przeznaczona do rozwiązywania problemów rozpraszania, a nie stanów związanych, takich jak atomy. W przypadku oddziaływania silnego wiążącego kwarki w nukleony przy niskich energiach, teoria zaburzeń nigdy nie dała wyników zgodnych z eksperymentami, a zatem wiarygodność obrazu „cząstek pośredniczących w siłach” jest wątpliwa. Podobnie w przypadku stanów związanych metoda zawodzi. W takich przypadkach interpretacja fizyczna musi zostać ponownie zbadana. Na przykład, obliczenia struktury atomowej w fizyce atomowej lub struktury molekularnej w chemii kwantowej nie mogą być łatwo powtórzone, jeśli w ogóle, przy użyciu obrazu „cząstek pośredniczących w siłach”.

Użycie obrazu „cząstek pośredniczących w działaniu” (FMPP) jest niepotrzebne w nierelatywistycznej mechanice kwantowej , a prawo Coulomba jest używane, jak podano w fizyce atomowej i chemii kwantowej, do obliczania zarówno stanów związanych, jak i rozproszenia. Nieperturbacyjną relatywistyczną teorię kwantową , w której zachowana jest niezmienność Lorentza, można osiągnąć, oceniając prawo Coulomba jako interakcję 4-przestrzenną przy użyciu 3-przestrzennego wektora pozycji elektronu odniesienia zgodnego z równaniem Diraca i trajektorii kwantowej drugiego elektronu, która zależy tylko od przeskalowanego czasu. Trajektoria kwantowa każdego elektronu w zespole jest wywnioskowana z prądu Diraca dla każdego elektronu przez ustawienie go równego polu prędkości pomnożonemu przez gęstość kwantową, obliczenie pola pozycji na podstawie całki pola prędkości w czasie, a na koniec obliczenie trajektorii kwantowej od wartości oczekiwanej pola pozycji. Trajektorie kwantowe są oczywiście zależne od spinu, a teorię można potwierdzić, sprawdzając, czy w przypadku zbioru fermionów przestrzegana jest zasada wykluczenia Pauliego .

Siły klasyczne

Siła wywierana przez jedną masę na drugą i siła wywierana przez jeden ładunek na drugi są uderzająco podobne. Oba wypadają jako kwadrat odległości między ciałami. Oba są proporcjonalne do iloczynu właściwości ciał, masy w przypadku grawitacji i ładunku w przypadku elektrostatyki.

Mają też uderzającą różnicę. Dwie masy przyciągają się, a dwie podobne ładunki odpychają się.

W obu przypadkach ciała wydają się oddziaływać na siebie na odległość. Pojęcie pola zostało wymyślone, aby pośredniczyć w interakcji między ciałami, eliminując w ten sposób potrzebę działania na odległość . Siła grawitacyjna jest pośredniczona przez pole grawitacyjne, a siła kulombowska jest pośredniczona przez pole elektromagnetyczne .

Siła grawitacji

Siła grawitacyjna wywierana na masę przez inną masę wynosi ${\ Displaystyle m}$${\ Displaystyle M}$

${\ Displaystyle \ mathbf {F} = - G {mM \ nad {r} ^ {2}} \ \ mathbf {\ kapelusz {r}} = m \ mathbf {g} \ lewo (\ mathbf {r} \ Prawidłowy),}$

gdzie G jest stałą grawitacyjną , r jest odległością między masami i jest wektorem jednostkowym od masy do masy . ${\displaystyle \mathbf {\kapelusz {r}}}$${\ Displaystyle M}$${\ Displaystyle m}$

Siłę można również zapisać

${\ Displaystyle \ mathbf {F} = m \ mathbf {g} \ lewo (\ mathbf {r} \ prawej)}$

gdzie jest pole grawitacyjne opisane równaniem pola ${\ Displaystyle \ mathbf {g} \ po lewej (\ mathbf {r} \ po prawej)}$

${\ Displaystyle \ nabla \ cdot \ mathbf {g} = -4 \ pi G \ rho _ {m}}$

gdzie jest gęstość masy w każdym punkcie przestrzeni. ${\ Displaystyle \ rho _ {m}}$

Siła kulombowska

Siła elektrostatyczna kulombowska na ładunek wywierany przez ładunek wynosi ( jednostki SI ) ${\displaystyle q}$${\displaystyle Q}$

${\ Displaystyle \ mathbf {F} = {1 \ ponad 4 \ pi \ varepsilon _ {0}} {qQ \ nad r ^ {2}} \ mathbf {\ kapelusz {r}}},}$

gdzie jest przenikalność próżni , jest separacją dwóch ładunków i jest wektorem jednostkowym w kierunku od ładunku do ładunku . ${\ Displaystyle \ varepsilon _ {0}}$${\ Displaystyle r}$${\displaystyle \mathbf {\kapelusz {r}}}$${\displaystyle Q}$${\displaystyle q}$

Siłę Coulomba można również zapisać w postaci pola elektrostatycznego :

${\ Displaystyle \ mathbf {F} = q \ mathbf {E} \ lewo (\ mathbf {r} \ po prawej)}$

gdzie

${\ Displaystyle \ nabla \ cdot \ mathbf {E} = {\ Frac {\ rho _ {q}} {\ varepsilon _ {0}}};}$

${\ Displaystyle \ rho _ {q}}$będąc gęstością ładunku w każdym punkcie przestrzeni.

Wirtualna wymiana cząstek

W teorii perturbacji siły generowane są przez wymianę wirtualnych cząstek . Mechanikę wymiany cząstek wirtualnych najlepiej opisać za pomocą całkowego sformułowania ścieżkowego mechaniki kwantowej. Istnieją jednak spostrzeżenia, które można uzyskać bez zagłębiania się w maszynerię całek po trajektorii, na przykład dlaczego klasyczne siły grawitacyjne i elektrostatyczne spadają jako odwrotność kwadratu odległości między ciałami.

Sformułowanie ścieżkowo-całkowe wymiany wirtualnej-cząstek

Wirtualna cząstka jest tworzona przez zakłócenie stanu próżni , a wirtualna cząstka zostaje zniszczona, gdy zostaje ponownie wchłonięta do stanu próżni przez inne zakłócenie. Wyobraża się, że zakłócenia są spowodowane ciałami, które oddziałują z polem wirtualnej cząstki.

Amplituda prawdopodobieństwa

Używając jednostek naturalnych , , podano amplitudę prawdopodobieństwa powstania, propagacji i zniszczenia wirtualnej cząstki, w sformułowaniu całki ścieżkowej przez ${\ Displaystyle \ hbar = c = 1}$

${\ Displaystyle Z \ equiv \ langle 0 | \ exp \ lewo (-i {\ kapelusz {H}} T \ po prawej) | 0 \ rangle = \ exp \ po lewej (-iET \ po prawej) = \ int D \ varphi \ ;\exp \left(i{\mathcal {S}}[\varphi ]\right)\;=\exp \left(iW\right)}$

gdzie jest operatorem hamiltonowskim , jest upływającym czasem, jest zmianą energii spowodowaną zaburzeniem, jest zmianą działania spowodowaną zaburzeniem, jest polem cząstki wirtualnej, całką jest po wszystkich ścieżkach i podano działanie klasyczne za pomocą ${\ Displaystyle {\ kapelusz {H}}}$${\displaystyle T}$${\ Displaystyle E}$${\displaystyle W=-ET}$${\displaystyle \varphi}$

${\ Displaystyle {\ mathcal {S}} [\ varphi ] = \ int \ operatorname {d} ^ {4}x \; {{\ mathcal {L}} [\ varphi (x)] \,}}$

gdzie jest gęstość Lagrange'a . ${\ Displaystyle {\ mathcal {L}} [\ varphi (x)]}$

Tutaj metryka czasoprzestrzeni jest podana przez

${\ Displaystyle \ eta _ {\ mu \ nu} = {\ zacząć {pmatrix} 1 i 0 i 0 i 0 \ \ 0 i 1 i 0 i 0 \ \ 0 i 0 i 1 i 0 \ \ 0 i 0 i 0 i 1 \ koniec {pmatrix}}.}$

Całkę po ścieżce często można przekształcić w postać

${\ Displaystyle Z = \ int \ exp \ lewo [i \ int d ^ {4} x \ lewo ({\ Frac {1} {2}} \ varphi {\ kapelusz {O}} \ varphi + J \ varphi \ prawo)\prawo]D\varphi }$

w którym jest operator różnicowy i funkcje czasoprzestrzeni . Pierwszy człon w argumencie reprezentuje wolną cząstkę, a drugi reprezentuje zakłócenie pola z zewnętrznego źródła, takiego jak ładunek lub masa. ${\ Displaystyle {\ kapelusz {O}}}$${\displaystyle \varphi}$${\ Displaystyle J}$

Całkę można zapisać (patrz Wspólne całki w kwantowej teorii pola )

${\ Displaystyle Z \ propto \ exp \ po lewej (iW \ po lewej (J \ po prawej) \ po prawej)}$

gdzie

${\ Displaystyle W \ po lewej (J \ po prawej) = - {1 \ ponad 2} \ iint d ^ {4} x \; d ^ {4} y \; J \ po lewej (x \ po prawej) D \ po lewej (xy \prawo)J\lewo(y\prawo)}$

jest zmianą działania spowodowaną zakłóceniami, a propagator jest rozwiązaniem ${\ Displaystyle D \ lewy (xy \ prawy)}$

${\ Displaystyle {\ kapelusz {O}} D \ po lewej (xy \ po prawej) = \ delta ^ {4} \ po lewej (xy \ po prawej)}$.

Energia interakcji

Zakładamy, że istnieją zaburzenia dwupunktowe reprezentujące dwa ciała oraz że zaburzenia te są nieruchome i stałe w czasie. Zakłócenia można zapisać

${\ Displaystyle J \ po lewej (x \ po prawej) = \ po lewej (J_ {1} + J_ {2} 0,0, 0 \ po prawej)}$

${\ Displaystyle J_ {1} = a_ {1} \ delta ^ {3} \ lewo ({\ vec {x}} - {\ vec {x}} _ {1} \ prawej)}$

${\ Displaystyle J_ {2} = a_ {2} \ delta ^ {3} \ lewo ({\ vec {x}} - {\ vec {x}} _ {2} \ prawej)}$

gdzie funkcje delta znajdują się w przestrzeni, zakłócenia znajdują się w i , a współczynniki i są siłą zakłóceń. ${\displaystyle {\vec {x}}_{1}}$${\displaystyle {\vec {x}}_{2}}$${\displaystyle a_{1}}$${\displaystyle a_{2}}$

Jeśli zaniedbujemy wzajemne oddziaływania zakłóceń, wówczas W staje się

${\ Displaystyle W \ po lewej (J \ po prawej) = - \ iint d ^ {4} x \; d ^ {4} y \; J_ {1} \ po lewej (x \ po prawej) {1 \ ponad 2} \ po lewej [D\lewo(xy\prawo)+D\lewo(yx\prawo)\prawo]J_{2}\lewo(y\prawo)}$,

które można napisać

${\ Displaystyle W \ lewo (J \ prawo) = - Ta_ {1} a_ {2} \ int {d ^ {3} k \ ponad (2 \ pi ) ^ {3}} \; D \ lewo ( k\right)\mid _{k_{0}=0}\;\exp \left(i{\vec {k}}\cdot \left({\vec {x}}_{1}-{\vec {x}}_{2}\prawo)\prawo)}$.

Oto transformata Fouriera ${\ Displaystyle D \ lewo (k \ prawo)}$

${\ Displaystyle {1 \ ponad 2} \ lewo [D \ lewo (xy \ prawo) + D \ lewo (yx \ prawo) \ prawo]}$.

Wreszcie, zmiana energii spowodowana zakłóceniami statycznymi próżni wynosi

${\ Displaystyle E = - {W \ nad T} = a_ {1} a_ {2} \ int {d ^ {3} k \ nad (2 \ pi ) ^ {3}} \; \; D \ lewo ( k\right)\mid _{k_{0}=0}\;\exp \left(i{\vec {k}}\cdot \left({\vec {x}}_{1}-{\vec {x}}_{2}\prawo)\prawo)}$.

Jeśli ta ilość jest ujemna, siła jest przyciągająca. Jeśli jest pozytywny, siła jest odpychająca.

Przykładami statycznych, nieruchomych, oddziałujących prądów są potencjał Yukawy , potencjał kulombowski w próżni i potencjał kulombowski w prostej plazmie lub gazie elektronowym .

Wyrażenie na energię oddziaływania można uogólnić do sytuacji, w której cząstki punktowe poruszają się, ale ruch jest powolny w porównaniu z prędkością światła. Przykładami są interakcja Darwina w próżni i interakcja Darwina w plazmie .

Wreszcie, wyrażenie na energię oddziaływania można uogólnić na sytuacje, w których zakłócenia nie są cząstkami punktowymi, ale prawdopodobnie ładunkami liniowymi, rurkami ładunków lub wirami prądu. Przykładami są dwa ładunki liniowe osadzone w plazmie lub gazie elektronowym , potencjał kulombowski między dwiema pętlami prądowymi osadzonymi w polu magnetycznym oraz oddziaływanie magnetyczne między pętlami prądowymi w prostej plazmie lub gazie elektronowym . Jak widać z przykładu oddziaływania kulombowskiego między rurkami ładunku, pokazanego poniżej, te bardziej skomplikowane geometrie mogą prowadzić do tak egzotycznych zjawisk, jak ułamkowe liczby kwantowe .

Wybrane przykłady

Potencjał Yukawy: Siła między dwoma nukleonami w jądrze atomowym

Rozważmy spin -0 gęstość Lagrange'a

${\ Displaystyle {\ mathcal {L}} [\ varphi (x)] = {1 \ ponad 2} \ lewo [\ lewo (\ częściowy \ varphi \ po prawej) ^ {2}-m ^ {2} \ varphi ^ {2}\prawo]}$.

Równanie ruchu dla tego Lagrange'a to równanie Kleina-Gordona

${\ Displaystyle \ częściowy ^ {2} \ Varphi + m ^ {2} \ Varphi = 0}$.

Jeśli dodamy zakłócenie, amplituda prawdopodobieństwa staje się

${\ Displaystyle Z = \ int D \ varphi \; \ exp \ lewo \ {i \ int d ^ {4} x \; \ lewo [{1 \ ponad 2} \ lewo (\ lewo (\ częściowe \ Varphi \ prawo )^{2}-m^{2}\varphi ^{2}\prawo)+J\varphi \prawo]\prawo\}}$.

Jeśli całkujemy przez części i pomijamy warunki brzegowe w nieskończoności, amplituda prawdopodobieństwa staje się

${\ Displaystyle Z = \ int D \ varphi \; \ exp \ lewo \ {i \ int d ^ {4} x \; \ lewo [-{1 \ ponad 2} \ varphi \ lewo (\ częściowy ^ {2} +m^{2}\prawo)\varphi +J\varphi \prawo]\prawo\}}$.

Przy amplitudzie w tej postaci widać, że propagator jest rozwiązaniem

${\ Displaystyle - \ lewo (\ częściowy ^ {2} + m ^ {2} \ po prawej) D \ po lewej (xy \ po prawej) = \ delta ^ {4} \ po lewej (xy \ po prawej)}$.

Z tego widać, że

${\ Displaystyle D \ lewo (k \ prawo) \ mid _ {k_ {0}= 0} \; = \; - {1 \ ponad {\ vec {k}} ^ {2} + m ^ {2}} }$.

Energia spowodowana zakłóceniami statycznymi staje się (patrz Wspólne całki w kwantowej teorii pola )

${\ Displaystyle E = - {a_ {1} a_ {2} \ ponad 4 \ pi r} \ exp \ lewo (-mr \ prawo)}$

z

${\ Displaystyle r ^ {2} = \ lewo ({\ vec {x}} _ {1} - {\ vec {x}} _ {2} \ prawej) ^ {2}}$

który jest atrakcyjny i ma zasięg

${\ Displaystyle {1 \ ponad m}}$.

Yukawa zaproponował, że pole to opisuje siłę między dwoma nukleonami w jądrze atomowym. Pozwoliło mu to przewidzieć zarówno zasięg, jak i masę cząstki, znanej obecnie jako pion , związanej z tym polem.

Elektrostatyka

Potencjał kulombowski w próżni

Rozważmy spin -1 Proca Lagrange'a z zaburzeniem

${\ Displaystyle {\ mathcal {L}} [\ varphi (x)] = - {1 \ ponad 4} F_ {\ mu \ nu} F ^ {\ mu \ nu} + {1 \ ponad 2} m ^ { 2}A_{\mu }A^{\mu }+A_{\mu }J^{\mu }}$

gdzie

${\ Displaystyle F_ {\ mu \ nu} = \ częściowy _ {\ mu} A_ {\ nu} - \ częściowy _ {\ nu} A_ {\ mu}}$,

opłata jest zachowana

${\ Displaystyle \ częściowy _ {\ mu} J ^ {\ mu} = 0}$,

i wybieramy miernik Lorenza

${\ Displaystyle \ częściowy _ {\ mu} A ^ {\ mu} = 0}$.

Ponadto zakładamy, że w zaburzeniu występuje tylko składnik czasowy . W języku potocznym oznacza to, że w miejscach zakłóceń występuje ładunek, ale nie ma prądów elektrycznych. ${\ Displaystyle J ^ {0}}$

Jeśli zastosujemy tę samą procedurę, co w przypadku potencjału Yukawy, stwierdzimy, że

${\ Displaystyle - {1 \ ponad 4} \ int d ^ {4} xF_ {\ mu \ nu} F ^ {\ mu \ nu} = - {1 \ ponad 4} \ int d ^ {4} x \ lewo (\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\right)\left(\partial ^{\mu }A^{\nu }-\partial ^{ \nu }A^{\mu }\prawo)}$

${\ Displaystyle = {1 \ ponad 2} \ int d ^ {4} x \; A_ {\ nu} \ lewo (\ częściowy ^ {2} A ^ {\ nu} - \ częściowy ^ {\ nu} \ częściowy _{\mu }A^{\mu }\right)={1 \over 2}\int d^{4}x\;A^{\mu }\left(\eta _{\mu \nu }\ częściowe ^{2}\right)A^{\nu },}$

co oznacza

${\ Displaystyle \ eta _ {\ mu \ alfa} \ po lewej (\ częściowy ^ {2} + m ^ {2} \ prawej) D ^ {\ alfa \ nu} \ po lewej (xy \ po prawej) = \ delta _ { \mu }^{\nu }\delta ^{4}\left(xy\right)}$

oraz

${\ Displaystyle D_ {\ mu \ nu} \ lewo (k \ po prawej) \ mid _ {k_ {0}= 0} \; = \; \ eta _ {\ mu \ nu {1 \ ponad -k ^ { 2}+m^{2}}.}$

To daje

${\ Displaystyle D \ lewo (k \ prawo) \ mid _ {k_ {0}= 0} \; = \; {1 \ ponad {\ vec {k}} ^ {2} + m ^ {2}}}$

dla czasowego propagatora i

${\ Displaystyle E = + {a_ {1} a_ {2} \ ponad 4 \ pi r} \ exp \ lewo (-mr \ prawo)}$

który ma przeciwny znak do przypadku Yukawy.

W granicy zerowej masy fotonu Lagranżian redukuje się do Lagrange'a dla elektromagnetyzmu

${\ Displaystyle E = {a_ {1} a_ {2} \ ponad 4 \ pi r}.}$

Dlatego energia sprowadza się do energii potencjalnej dla siły Coulomba i współczynników i jest proporcjonalna do ładunku elektrycznego. W przeciwieństwie do przypadku Yukawy, podobnie jak ciała, w tym elektrostatycznym przypadku odpychają się nawzajem. ${\displaystyle a_{1}}$${\displaystyle a_{2}}$

Potencjał kulombowski w prostej plazmie lub gazie elektronowym

Fale plazmowe

Relacja dyspersji dla fal plazmowych jest

${\ Displaystyle \ omega ^ {2} = \ omega _ {p} ^ {2} + \ gamma \ lewo (\ omega \ prawo) {T_ {e} \ nad m} {\ vec {k}} ^ {2 }.}$

gdzie jest częstotliwość kątowa fali, ${\ Displaystyle \ omega}$

${\ Displaystyle \ omega _ {p} ^ {2} = {4 \ pi ne ^ {2} \ nad m}}$

to częstotliwość plazmy , to wielkość ładunku elektronu , to masa elektronu , to temperatura elektronu ( stała Boltzmanna równa jeden) i jest czynnikiem, który zmienia się wraz z częstotliwością od jednego do trzech. Przy wysokich częstotliwościach, rzędu częstotliwości plazmy, kompresja płynu elektronowego jest procesem adiabatycznym i wynosi trzy. Przy niskich częstotliwościach kompresja jest procesem izotermicznym i jest równa jedności. Efekty opóźnienia zostały pominięte przy uzyskiwaniu zależności dyspersji fal plazmowych. ${\displaystyle e}$${\ Displaystyle m}$${\displaystyle T_{e}}$${\ Displaystyle \ gamma \ lewo (\ omega \ prawo)}$${\ Displaystyle \ gamma \ lewo (\ omega \ prawo)}$${\ Displaystyle \ gamma \ lewo (\ omega \ prawo)}$

Dla niskich częstotliwości relacja dyspersji staje się

${\ Displaystyle {\ vec {k}} ^ {2} + {\ vec {k}} _ {D} ^ {2} = 0}$

gdzie

${\ Displaystyle k_ {D} ^ {2} = {4 \ pi ne ^ {2} \ nad T_ {e}}}$

jest liczbą Debye'a, która jest odwrotnością długości Debye'a . Sugeruje to, że propagator jest

${\ Displaystyle D \ lewo (k \ po prawej) \ mid _ {k_ {0} = 0} \; = \; {1 \ ponad {\ vec {k}} ^ {2} + k_ {D} ^ {2 }}}$.

W rzeczywistości, jeśli efekty opóźnienia nie są pomijane, to relacja dyspersji wynosi

${\ Displaystyle -k_ {0} ^ {2} + {\ vec {k}} ^ {2} + k_ {D} ^ {2} - {m \ nad T_ {e}} k_ {0} ^ {2} }=0,}$

co rzeczywiście daje zgadywany propagator. Ten propagator jest taki sam jak masywny propagator kulombowski o masie równej odwrotnej długości Debye'a. Energia interakcji jest zatem

${\ Displaystyle E = {a_ {1} a_ {2} \ ponad 4 \ pi r} \ exp \ lewo (-k_ {D} r \ po prawej).}$

Potencjał Coulomba jest ekranowany na skalach długości o długości Debye'a.

Plazmony

W gazie elektronowym kwantowym fale plazmy są znane jako plazmony . Przesiewanie Debye'a zostaje zastąpione badaniem Thomas-Fermi, aby uzyskać plon

${\ Displaystyle E = {a_ {1} a_ {2} \ ponad 4 \ pi r} \ exp \ lewo (-k_ {s} r \ po prawej)}$

gdzie jest odwrotność długości przesiewania Thomasa-Fermiego

${\ Displaystyle k_ {s} ^ {2} = {6 \ pi ne ^ {2} \ nad \ epsilon _ {F}}}$

i jest energią Fermiego${\ Displaystyle \ epsilon _ {F}}$

${\ Displaystyle \ epsilon _ {F} = {\ Frac {\ Hbar ^ {2}} {2 m}} \ lewo ({3 \ pi ^ {2} n} \ po prawej) ^ {2/3} \ ,. }$

Wyrażenie to można wyprowadzić z potencjału chemicznego gazu elektronowego iz równania Poissona . Potencjał chemiczny gazu elektronowego w pobliżu równowagi jest stały i podany przez

${\ Displaystyle \ mu =-e \ varphi + \ epsilon _ {F}}$

gdzie jest potencjał elektryczny . Linearyzacja energii Fermiego do pierwszego rzędu w fluktuacji gęstości i połączenie z równaniem Poissona daje długość ekranu. Nośnikiem siły jest kwantowa wersja fali plazmowej . ${\displaystyle \varphi}$

Dwa ładunki liniowe osadzone w plazmie lub gazie elektronowym

Rozważamy linię ładunku o osi w kierunku z zatopioną w gazie elektronowym

${\ Displaystyle J_ {1} \ lewo (x \ prawy) = {a_ {1} \ nad L_ {B}} {1 \ nad 2 \ pi r} \ delta ^ {2} \ po lewej (r \ po prawej)}$

gdzie jest odległością w płaszczyźnie xy od linii ładunku, jest szerokością materiału w kierunku z. Indeks górny 2 wskazuje, że delta Diraca jest w dwóch wymiarach. Propagatorem jest ${\ Displaystyle r}$${\ Displaystyle L_ {B}}$

${\ Displaystyle D \ lewo (k \ po prawej) \ mid _ {k_ {0} = 0} \; = \; {1 \ ponad {\ vec {k}} ^ {2} + k_ {DS} ^ {2 }}}$

gdzie jest albo odwrotną długością przesiewania Debye-Hückel, albo odwrotną długością przesiewania Thomasa-Fermiego . ${\displaystyle k_{DS}}$

Energia interakcji to

${\ Displaystyle E = \ lewo ({a_ {1} \ a_ {2} \ ponad 2 \ pi L_ {B}} \ prawo) \ int _ {0} ^ {\ infty} {{k \; dk \ ;} \over k^{2}+k_{Ds}^{2}}{\mathcal {J}}_{0}\left(kr_{12}\right)=\left({a_{1}\ ,a_{2} \over 2\pi L_{B}}\right)K_{0}\left(k_{Ds}r_{12}\right)}$

gdzie

${\ Displaystyle {\ mathcal {J}} _ {n} \ lewo (x \ prawo)}$

oraz

${\displaystyle K_{0}\lewo (x\prawo)}$

są funkcjami Bessela i jest odległością między dwoma opłatami liniowymi. W celu uzyskania energii interakcji wykorzystaliśmy całek (patrz Powszechne całki w kwantowej teorii pola ) ${\ Displaystyle r_ {12}}$

${\ Displaystyle \ int _ {0} ^ {2 \ pi} {d \ varphi \ ponad 2 \ pi} \ exp \ po lewej (ip \ cos \ po lewej (\ varphi \ po prawej) \ po prawej) = {\ mathcal {J }}_{0}\lewo(p\prawo)}$

oraz

${\ Displaystyle \ int _ {0} ^ {\ infty} {{k \; dk \;} \ ponad k ^ {2} + m ^ {2}} {\ mathcal {J}} _ {0} \ lewo (kr\right)=K_{0}\lewo(mr\prawo).}$

Dla , mamy ${\ Displaystyle k_ {DS} r_ {12} \ ll 1}$

${\ Displaystyle K_ {0} \ lewo (k_ {DS} r_ {12} \ prawo) \ rightarrow - \ ln \ lewo ({k_ {DS} r_ {12} \ ponad 2} \ po prawej) + 0,5772.}$

Potencjał kulombowski między dwiema pętlami prądowymi osadzonymi w polu magnetycznym

Energia interakcji dla wirów

Rozważamy gęstość ładunku w rurze o osi wzdłuż pola magnetycznego osadzonego w gazie elektronowym

${\ Displaystyle J_ {1} \ lewo (x \ prawo) = {a_ {1} \ nad L_ {b}} {1 \ nad 2 \ pi r} \ delta ^ {2} \ po lewej (r-r_ {B1 }\Prawidłowy)}$

gdzie jest odległość od środka prowadzącego , jest szerokością materiału w kierunku pola magnetycznego ${\ Displaystyle r}$${\ Displaystyle L_ {B}}$

${\ Displaystyle R_ {B1} = {{\ sqrt {4 \ pi}} m_ {1} v_ {1} \ nad a_ {1} B} = {\ sqrt {2 \ hbar \ nad m_ {1} \ omega _{C}}}}$

gdzie jest częstotliwość cyklotronu ( jednostki Gaussa )

${\ Displaystyle \ omega _ {c} = {a_ {1} B \ ponad {\ sqrt {4 \ pi}} m_ {1} c}}$

oraz

${\ Displaystyle V_ {1} = {\ sqrt {2 \ hbar \ omega _ {c} \ nad m_ {1}}}}$

to prędkość cząstki wokół pola magnetycznego, a B to wielkość pola magnetycznego. Wzór na prędkość pochodzi z ustawienia klasycznej energii kinetycznej równej odległościom między poziomami Landaua w kwantowej obróbce naładowanej cząstki w polu magnetycznym.

W tej geometrii można zapisać energię interakcji

${\ Displaystyle E = \ lewo ({a_ {1} \, a_ {2} \ ponad 2 \ pi L_ {B}} \ prawej) \ int _ {0} ^ {\ infty} {k \; dk \; }D\left(k\right)\mid _{k_{0}=k_{B}=0}{\mathcal {J}}_{0}\left(kr_{B1}\right){\mathcal { J}}_{0}\left(kr_{B2}\right){\mathcal {J}}_{0}\left(kr_{12}\right)}$

gdzie jest odległość między środkami pętli prądowych i ${\ Displaystyle r_ {12}}$

${\ Displaystyle {\ mathcal {J}} _ {n} \ lewo (x \ prawo)}$

jest funkcją Bessela pierwszego rodzaju. W celu uzyskania energii oddziaływania wykorzystaliśmy całkę

${\ Displaystyle \ int _ {0} ^ {2 \ pi} {d \ varphi \ ponad 2 \ pi} \ exp \ po lewej (ip \ cos \ po lewej (\ varphi \ po prawej) \ po prawej) = {\ mathcal {J }}_{0}\lewo(p\prawo).}$

Pole elektryczne z powodu zaburzenia gęstości

Chemiczny potencjał bliskich równowadze, podaje

${\ Displaystyle \ mu = - e \ varphi + N \ hbar \ omega _ {c} = N_ {0} \ hbar \ omega _ {c}}$

gdzie to potencjalna energia elektronu w potencjale elektrycznym , a i oznacza liczbę cząstek w gazie elektronów w nieobecności i w obecności potencjału elektrostatycznego, odpowiednio. ${\displaystyle -e\varphi}$${\displaystyle N_{0}}$${\ Displaystyle N}$

Wahania gęstości są wtedy

${\ Displaystyle \ delta n = {e \ varphi \ nad \ hbar \ omega _ {c} A_ {M} L_ {B}}}$

gdzie jest obszar materiału w płaszczyźnie prostopadłej do pola magnetycznego. ${\ Displaystyle A_ {M}}$

Równanie różniczkowe Poissona plony

${\ Displaystyle \ lewo (k ^ {2} + k_ {B} ^ {2} \ po prawej) \ varphi = 0}$

gdzie

${\ Displaystyle k_ {B} ^ {2} = {4 \ pi e ^ {2} \ nad \ hbar \ omega _ {c} A_ {M} L_ {B}}.}$

Propagator jest wtedy

${\ Displaystyle D \ lewo (k \ prawo) \ mid _ {k_ {0}= k_ {B} = 0} = {1 \ ponad k ^ {2} + k_ {B} ^ {2}}}$

a energia interakcji staje się

${\ Displaystyle E = \ lewo ({a_ {1} \ a_ {2} \ ponad 2 \ pi L_ {B}} \ prawo) \ int _ {0} ^ {\ infty} {{k \; dk \ ;} \over k^{2}+k_{B}^{2}}{\mathcal {J}}_{0}\left(kr_{B1}\right){\mathcal {J}}_{0 }\left(kr_{B2}\right){\mathcal {J}}_{0}\left(kr_{12}\right)=\left({2e^{2} \over L_{B}}\ po prawej)\int _{0}^{\infty }{{k\;dk\;} \over k^{2}+k_{B}^{2}r_{B}^{2}}{\mathcal {J}}_{0}^{2}\left(k\right){\mathcal {J}}_{0}\left(k{r_{12} \over r_{B}}\right)}$

gdzie w drugiej równości ( jednostki Gaussa ) zakładamy, że wiry miały taką samą energię i ładunek elektronu.

Analogicznie plazmony The nośnik siła jest wersja kwantową górnej hybrydowego drgań , który jest podłużny fali w osoczu , które rozprzestrzenia się w kierunku prostopadłym do pola magnetycznego.

Prądy z momentem pędu

Prądy funkcji delta

Rysunek 1. Energia oddziaływania w funkcji r dla stanów momentu pędu o wartości jeden. Krzywe są identyczne jak te dla dowolnych wartości . Długości są w jednostkach , a energia w jednostkach . Tutaj . Zauważ, że istnieją lokalne minima dla dużych wartości .${\ Displaystyle {\ mathit {l}} = {{\ mathit {l}} ^ {\ prime}}}$${\displaystyle r_{\mathit {l}}}$${\ Displaystyle \ lewo ({e ^ {2} \ nad L_ {B}} \ po prawej)}$${\ Displaystyle r = r_ {12}}$${\ Displaystyle k_ {B}}$

Rysunek 2. Energia oddziaływania w funkcji r dla stanów momentu pędu o wartościach jeden i pięć.

Rysunek 3. Energia oddziaływania w funkcji r dla różnych wartości theta. Najniższa energia jest dla lub . Najwyższa wykreślona energia dotyczy . Długości podano w jednostkach .${\ Displaystyle \ theta = {\ pi \ ponad 4}}$${\ Displaystyle {{\ mathit {l}} \ nad {\ mathit {l}} ^ {\ prime}} = 1}$${\ Displaystyle \ theta = 0,90 {\ pi \ ponad 4}}$${\ Displaystyle R_ {{\ mathit {l}} {\ mathit {l}} ^ {\ prime}}}$

Rysunek 4. Energie stanu podstawowego dla parzystych i nieparzystych wartości momentu pędu. Energia jest kreślona na osi pionowej, a r na poziomej. Gdy całkowity moment pędu jest równy, minimum energii występuje, gdy lub . Gdy całkowity moment pędu jest nieparzysty, nie ma całkowitych wartości momentu pędu, które będą leżeć w minimum energii. Dlatego istnieją dwa stany, które leżą po obu stronach minimum. Ponieważ całkowita energia jest wyższa niż w przypadku, gdy dla danej wartości .${\ Displaystyle {{\ mathit {l}} = {\ mathit {l}} ^ {\ prime}}}$${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = {1 \ ponad 2}}$${\ Displaystyle {{\ mathit {l}} \ neq {\ mathit {l}} ^ {\ prime}}}$${\ Displaystyle {{\ mathit {l}} = {\ mathit {l}} ^ {\ prime}}}$${\ Displaystyle {{\ mathit {l}} ^ {*}}}$

W przeciwieństwie do prądów klasycznych, kwantowe pętle prądowe mogą mieć różne wartości promienia Larmora dla danej energii. Poziomy Landaua , stany energetyczne naładowanej cząstki w obecności pola magnetycznego, są wielokrotnie zdegenerowane . Pętle prądowe odpowiadają stanom momentu pędu naładowanej cząstki, która może mieć taką samą energię. W szczególności gęstość ładunku osiąga szczyt wokół promieni

${\displaystyle r_{\mathit {l}}={\sqrt {\mathit {l}}}\;r_{B}\;\;\;{\mathit {l}}=0,1,2,\ doty }$

gdzie jest liczba kwantowa momentu pędu . Kiedy odzyskamy klasyczną sytuację, w której elektron krąży wokół pola magnetycznego w promieniu Larmora . Jeżeli prądy dwóch momentów pędu i oddziałują ze sobą i założymy, że gęstości ładunków są funkcjami delta w promieniu , to energia oddziaływania jest równa ${\displaystyle {\mathit {l}}}$${\displaystyle {\mathit {l}}=1}$${\ Displaystyle {\ mathit {l}} _ {} ^ {}> 0}$${\ Displaystyle {\ mathit {l}} ^ {\ prime} \ geq {\ mathit {l}} _ {} ^ {}}$${\displaystyle r_{\mathit {l}}}$

${\ Displaystyle E = \ lewo ({2e ^ {2} \ nad L_ {B}} \ po prawej) \ int _ {0} ^ {\ infty} {{k \; dk \;} \ nad k ^ {2 }+k_{B}^{2}r_{\mathit {l}}^{2}}\;{\mathcal {J}}_{0}\left(k\right)\;{\mathcal {J }}_{0}\left({\sqrt {{{\mathit {l}}^{\prime }} \over {\mathit {l}}}}\;k\right)\;{\mathcal { J}}_{0}\left(k{r_{12} \over r_{\mathit {l}}}\right).}$

Energia interakcji dla jest podana na rysunku 1 dla różnych wartości . Energia dla dwóch różnych wartości jest podana na rysunku 2. ${\ Displaystyle {\ mathit {l}} = {\ mathit {l}} ^ {\ prime}}$${\ Displaystyle k_ {B} r_ {\ mathit {l}}}$

Quasicząstki

Dla dużych wartości momentu pędu energia może mieć lokalne minima w odległościach innych niż zero i nieskończoność. Można liczbowo zweryfikować, że minima występują przy

${\ Displaystyle r_ {12} = r_ {{\ mathit {l}} {\ mathit {l}} ^ {\ prime}} = {\ sqrt {{\ mathit {l}} + {\ mathit {l}} ^{\prime }}}\;r_{B}.}$

Sugeruje to, że para cząstek, które są związane i rozdzielone odległością, działa jak pojedyncza quasicząstka z momentem pędu . ${\ Displaystyle R_ {{\ mathit {l}} {\ mathit {l}} ^ {\ prime}}}$${\ Displaystyle {\ mathit {l}} + {\ mathit {l}} ^ {\ prime}}$

Jeśli skalujemy długości jako , wtedy energia interakcji staje się ${\ Displaystyle R_ {{\ mathit {l}} {\ mathit {l}} ^ {\ prime}}}$

${\ Displaystyle E = \ lewo ({2e ^ {2} \ nad L_ {B}} \ po prawej) \ int _ {0} ^ {\ infty} {{k \; dk \;} \ nad k ^ {2 }+k_{B}^{2}r_{{\mathit {l}}{\mathit {l}}^{\prime }}^{2}}\;{\mathcal {J}}_{0} \left(\cos \theta \;k\right)\;{\mathcal {J}}_{0}\left(\sin \theta \;k\right)\;{\mathcal {J}}_{ 0}\left(k{r_{12} \over r_{{\mathit {l}}{\mathit {l}}^{\prime }}}\right)}$

gdzie

${\ Displaystyle \ tan \ theta = {\ sqrt {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {\ prime}}}.}$

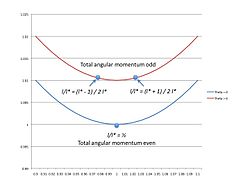
Wartość przy której energia jest minimalna , jest niezależna od stosunku . Jednak wartość energii na minimum zależy od stosunku. Najniższa energia minimalna występuje, gdy ${\ Displaystyle r_ {12}}$${\ Displaystyle r_ {12} = r_ {{\ mathit {l}} {\ mathit {l}} ^ {\ prime}}}$${\ Displaystyle \ tan \ theta = {\ sqrt {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {\ prime}}}}$

${\ Displaystyle {{\ mathit {l}} \ nad {\ mathit {l}} ^ {\ prime}} = 1.}$

Gdy stosunek różni się od 1, to minimum energii jest wyższe (rysunek 3). Dlatego dla parzystych wartości całkowitego pędu najniższa energia występuje, gdy (rysunek 4)

${\ Displaystyle {\ mathit {l}} = {\ mathit {l}} ^ {\ prime} = 1}$

lub

${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = {1 \ ponad 2}}$

gdzie całkowity moment pędu jest zapisany jako

${\ Displaystyle {{\ mathit {l}} ^ {*}} = {\ mathit {l}} + {{\ mathit {l}} ^ {\ prime}}.}$

Gdy całkowity moment pędu jest nieparzysty, minima nie mogą wystąpić dla Najniższe stany energetyczne dla nieparzystego całkowitego momentu pędu występują, gdy ${\ Displaystyle {{\ mathit {l}} = {\ mathit {l}} ^ {\ prime}}.}$

${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = \; {{\ mathit {l}} ^ {*} \ pm 1 \ ponad 2 {\ mathit { l}}^{*}}}$

lub

${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = {1 \ ponad 3}, {2 \ ponad 5}, {3 \ ponad 7}, {\ mbox {itp.,}}}$

oraz

${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = {2 \ ponad 3}, {3 \ ponad 5}, {4 \ ponad 7}, {\ mbox {itp.,}}}$

które pojawiają się również jako szeregi dla współczynnika wypełnienia w ułamkowym kwantowym efekcie Halla .

Gęstość ładunku rozłożona na funkcję falową

Gęstość ładunku nie jest w rzeczywistości skoncentrowana w funkcji delta. Ładunek jest rozłożony na funkcję falową. W takim przypadku gęstość elektronowa wynosi

${\ Displaystyle {1 \ nad \ pi r_ {B} ^ {2} L_ {B}} {1 \ nad n!} \ lewo ({r \ nad r_ {B}} \ po prawej) ^ {2 {\ mathit {l}}}\exp \left(-{r^{2} \over r_{B}^{2}}\right).}$

Energia interakcji staje się

${\ Displaystyle E = \ lewo ({2e ^ {2} \ nad L_ {B}} \ po prawej) \ int _ {0} ^ {\ infty} {{k \; dk \;} \ nad k ^ {2 }+k_{B}^{2}r_{B}^{2}}\;M\left({\mathit {l}}+1,1,-{k^{2} \over 4}\right )\;M\left({\mathit {l}}^{\prime }+1,1,-{k^{2} \over 4}\right)\;{\mathcal {J}}_{0 }\left(k{r_{12} \over r_{B}}\right)}$

gdzie jest konfluentną funkcją hipergeometryczną lub funkcją Kummera . W celu uzyskania energii interakcji wykorzystaliśmy całkę (patrz Powszechne całki w kwantowej teorii pola ) ${\ Displaystyle M}$

${\ Displaystyle {2 \ ponad n!} \ int _ {0} ^ {\ infty} {dr} \; r ^ {2n + 1} \ exp \ lewo (-r ^ {2} \ po prawej) J_ {0 }\left(kr\right)=M\left(n+1,1,-{k^{2} \over 4}\right).}$

Podobnie jak w przypadku ładunków delta, wartość, w której energia jest lokalnym minimum, zależy tylko od całkowitego momentu pędu, a nie od momentu pędu poszczególnych prądów. Podobnie jak w przypadku ładunków w funkcji delta, energia w minimum wzrasta, gdy stosunek pędu kątowego zmienia się od jedności. Dlatego seria ${\ Displaystyle r_ {12}}$

${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = {1 \ ponad 3}, {2 \ ponad 5}, {3 \ ponad 7}, {\ mbox {itp.,}}}$

oraz

${\ Displaystyle {{\ mathit {l}} \ ponad {\ mathit {l}} ^ {*}} = {2 \ ponad 3}, {3 \ ponad 5}, {4 \ ponad 7}, {\ mbox {itp.,}}}$

pojawiają się również w przypadku ładunków rozłożonych przez funkcję falową.

Laughlin falowa jest ansatz dla funkcji falowej kwazicząstka. Jeśli wartość oczekiwaną energii interakcji przejmie się z funkcji falowej Laughlina , szeregi te również zostaną zachowane.

Magnetostatyka

Interakcja Darwina w próżni

Naładowana poruszająca się cząstka może generować pole magnetyczne, które wpływa na ruch innej naładowanej cząstki. Wersja statyczna tego efektu nazywana jest interakcją Darwina . Aby to obliczyć, rozważ prądy elektryczne w przestrzeni generowane przez poruszający się ładunek

${\ Displaystyle {\ vec {J}} _ {1} \ lewo ({\ vec {x}} \ po prawej) = a_ {1} {\ vec {v}} _ {1} \ delta ^ {3} \ w lewo({\vec {x}}-{\vec {x}}_{1}\w prawo)}$

z porównywalnym wyrażeniem dla . ${\ Displaystyle {\ vec {J}} _ {2}}$

Transformata Fouriera tego prądu to

${\ Displaystyle {\ vec {J}} _ {1} \ po lewej ({\ vec {k}} \ po prawej) = a_ {1} {\ vec {v}} _ {1} \ exp \ po lewej (i { \vec {k}}\cdot {\vec {x}}_{1}\prawo).}$

Prąd można rozłożyć na część poprzeczną i podłużną (patrz rozkład Helmholtza ).

${\ Displaystyle {\ vec {J}} _ {1} \ lewo ({\ vec {k}} \ prawo) = a_ {1} \ lewo [1-{\ kapelusz {k}} {\ kapelusz {k} }\right]\cdot {\vec {v}}_{1}\exp \left(i{\vec {k}}\cdot {\vec {x}}_{1}\right)+a_{1 }\left[{\kapelusz {k}}{\kapelusz {k}}\right]\cdot {\vec {v}}_{1}\exp \left(i{\vec {k}}\cdot { \vec {x}}_{1}\prawo).}$

Kapelusz wskazuje wektor jednostkowy . Ostatni termin znika, ponieważ

${\ Displaystyle {\ vec {k}} \ cdot {\ vec {J}} = - k_ {0}J ^ {0} \ rightarrow 0,}$

co wynika z zachowania ładunku. Tutaj znika, ponieważ rozważamy siły statyczne. ${\displaystyle k_{0}}$

Z prądem w tej postaci można zapisać energię oddziaływania

${\ Displaystyle E = a_ {1} a_ {2} \ int {d ^ {3} k \ ponad (2 \ pi ) ^ {3}} \; \; D \ lewo (k \ po prawej) \ mid _ { k_{0}=0}\;{\vec {v}}_{1}\cdot \left[1-{\hat {k}}{\hat {k}}\right]\cdot {\vec { v}}_{2}\;\exp \left(i{\vec {k}}\cdot \left(x_{1}-x_{2}\right)\right)}$.

Równanie propagatora dla Proca Lagrange'a to

${\ Displaystyle \ eta _ {\ mu \ alfa} \ po lewej (\ częściowy ^ {2} + m ^ {2} \ prawej) D ^ {\ alfa \ nu} \ po lewej (xy \ po prawej) = \ delta _ { \mu }^{\nu }\delta ^{4}\lewo(xy\prawo).}$

Spacelike rozwiązanie

${\ Displaystyle D \ lewo (k \ prawo) \ mid _ {k_ {0}= 0} \; = \; - {1 \ ponad {\ vec {k}} ^ {2} + m ^ {2}} ,}$

co daje

${\ Displaystyle E = - a_ {1} a_ {2} \ int {d ^ {3} k \ ponad (2 \ pi ) ^ {3}} \; \; {{\ vec {v}} _ {1 }\cdot \left[1-{\hat {k}}{\hat {k}}\right]\cdot {\vec {v}}_{2} \over {\vec {k}}^{2 }+m^{2}}\;\exp \left(i{\vec {k}}\cdot \left(x_{1}-x_{2}\right)\right)}$

który ocenia (patrz Wspólne całki w kwantowej teorii pola )

${\ Displaystyle E = - {1 \ ponad 2} {a_ {1} a_ {2} \ ponad 4 \ pi r} e ^ {-mr} \ lewo \ {2 \ nad \ lewo (mr \ po prawej) ^ {2}}\left(e^{mr}-1\right)-{2 \over mr}\right\}{\vec {v}}_{1}\cdot \left[1+{\hat { r}}{\kapelusz {r}}\prawo]\cdot {\vec {v}}_{2}}$

co sprowadza się do

${\ Displaystyle E = - {1 \ ponad 2} {a_ {1} a_ {2} \ ponad 4 \ pi r {\ vec {v}}_ {1} \ cdot \ lewo [1 + {\ kapelusz { r}}{\kapelusz {r}}\prawo]\cdot {\vec {v}}_{2}}$

w granicach małego m. Energia interakcji jest ujemną Lagrange'a interakcji. Dla dwóch podobnych cząstek poruszających się w tym samym kierunku oddziaływanie jest atrakcyjne, co jest przeciwieństwem oddziaływania kulombowskiego.

Interakcja Darwina w plazmie

W plazmie zależność dyspersyjna dla fali elektromagnetycznej to ( ) ${\displaystyle c=1}$

${\ Displaystyle k_ {0} ^ {2} = \ omega _ {p} ^ {2} + {\ vec {k}} ^ {2}}$

co oznacza

${\ Displaystyle D \ lewo (k \ prawo) \ mid _ {k_ {0} = 0} \; = \; - {1 \ ponad {\ vec {k}} ^ {2} + \ omega _ {p} ^{2}}.}$

Tutaj jest częstotliwość osocze . Energia interakcji jest zatem ${\ Displaystyle \ omega _ {p}}$

${\ Displaystyle E = - {1 \ ponad 2} {a_ {1} a_ {2} \ ponad 4 \ pi r {\ vec {v}}_ {1} \ cdot \ lewo [1 + {\ kapelusz { r}}{\hat {r}}\right]\cdot {\vec {v}}_{2}\;e^{-\omega _{p}r}\left\{2 \over \left (\omega _{p}r\right)^{2}}\left(e^{\omega _{p}r}-1\right)-{2 \over \omega _{p}r}\right \}.}$

Oddziaływanie magnetyczne między pętlami prądowymi w prostej plazmie lub gazie elektronowym

Energia interakcji

Rozważmy rurkę prądu obracającą się w polu magnetycznym osadzoną w prostej plazmie lub gazie elektronowym. Prąd, który leży w płaszczyźnie prostopadłej do pola magnetycznego, określa się jako

${\ Displaystyle {\ vec {J}} _ {1} \ lewo ({\ vec {x}} \ prawej) = a_ {1} v_ {1} {1 \ ponad 2 \ pi rL_ {B}} \; \delta ^{2}\left(r-r_{B1}\right)\;\left({{\hat {b}}\times {\hat {r}}}\right)}$

gdzie

${\ Displaystyle R_ {B1} = {{\ sqrt {4 \ pi}} m_ {1} v_ {1} \ nad a_ {1} B}}$

i jest wektorem jednostkowym w kierunku pola magnetycznego. Tutaj wskazuje wymiar materiału w kierunku pola magnetycznego. Prąd poprzeczny prostopadły do wektora falowego napędza falę poprzeczną . ${\displaystyle {\kapelusz {b}}}$${\ Displaystyle L_ {B}}$

Energia interakcji to

${\ Displaystyle E = \ lewo ({a_ {1} \ a_ {2} \ ponad 2 \ pi L_ {B}} \ prawo) v_ {1} \ v_ {2} \ \ int _ {0} ^{\infty }{k\;dk\;}D\left(k\right)\mid _{k_{0}=k_{B}=0}{\mathcal {J}}_{1}\left (kr_{B1}\right){\mathcal {J}}_{1}\left(kr_{B2}\right){\mathcal {J}}_{0}\left(kr_{12}\right) }$

gdzie jest odległość między środkami pętli prądowych i ${\ Displaystyle r_ {12}}$

${\ Displaystyle {\ mathcal {J}} _ {n} \ lewo (x \ prawo)}$

jest funkcją Bessela pierwszego rodzaju. W celu uzyskania energii oddziaływania wykorzystaliśmy całek

${\ Displaystyle \ int _ {0} ^ {2 \ pi} {d \ varphi \ ponad 2 \ pi} \ exp \ po lewej (ip \ cos \ po lewej (\ varphi \ po prawej) \ po prawej) = {\ mathcal {J }}_{0}\lewo(p\prawo)}$

oraz

${\ Displaystyle \ int _ {0} ^ {2 \ pi} {d \ varphi \ ponad 2 \ pi} \ cos \ po lewej (\ varphi \ po prawej) \ exp \ po lewej (ip \ cos \ po lewej (\ varphi \ po prawej) )\right)=i{\mathcal {J}}_{1}\left(p\right).}$

Zobacz Wspólne całki w kwantowej teorii pola .

Prąd w plazmie ograniczony do płaszczyzny prostopadłej do pola magnetycznego generuje niezwykłą falę . Ta fala generuje prądy Halla, które oddziałują i modyfikują pole elektromagnetyczne. Relacja dyspersji nadzwyczajnych fal jest

${\ Displaystyle -k_ {0}^ {2} + {\ vec {k}} ^ {2} + \ omega _ {p} ^ {2} {\ lewo (k_ {0} ^ {2} - \ omega _{p}^{2}\right) \over \left(k_{0}^{2}-\omega _{H}^{2}\right)}=0,}$

co daje propagatorowi

${\ Displaystyle D \ lewo (k \ prawo) \ mid _ {k_ {0}= k_ {B} = 0} \; = \; - \ lewo ({1 \ ponad {\ vec {k}} ^ {2 }+k_{X}^{2}}\prawo)}$

gdzie

${\ Displaystyle k_ {X} \ równoważnik {\ omega _ {p} ^ {2} \ nad \ omega _ {H}}}$

analogicznie do propagatora Darwina. Tutaj górna częstotliwość hybrydowa jest dana przez

${\ Displaystyle \ omega _ {H} ^ {2} = \ omega _ {p} ^ {2} + \ omega _ {c} ^ {2}}$

częstotliwości cyklotron jest przez ( jednostki Gaussa )

${\ Displaystyle \ omega _ {c} = {EB \ nad mc}}$

i częstotliwość plazmy ( jednostki Gaussa )

${\ Displaystyle \ omega _ {p} ^ {2} = {4 \ pi ne ^ {2} \ nad m}.}$

Tutaj n to gęstość elektronów, e to wielkość ładunku elektronu, a m to masa elektronu.

Energia interakcji staje się, dla podobnych prądów,

${\ Displaystyle E = - \ lewo ({a ^ {2} \ ponad 2 \ pi L_ {B}} \ prawej) v ^ {2} \ \ int _ {0} ^ {\ infty} {k \; dk \over {\vec {k}}^{2}+k_{X}^{2}}{\mathcal {J}}_{1}^{2}\left(kr_{B}\right){ \mathcal {J}}_{0}\left(kr_{12}\right)}$

Limit małej odległości między pętlami prądowymi

W granicy, że odległość między pętlami prądowymi jest niewielka,

${\ Displaystyle E = - E_ {0} \; I_ {1} \ lewo (\ mu \ prawo) K_ {1} \ lewo (\ mu \ prawo)}$