Afiniczna grupa symetryczna - Affine symmetric group

W afiniczne grupy symetryczne są rodziną struktur matematycznych opisujących symetrie na osi liczbowej i regularnym trójkątnym kafli samolotu, a także związanych z obiektami wyższych wymiarów. Każda z nich jest nieskończonym rozszerzeniem skończonej grupy symetrycznej , grupy permutacji (przegrupowań) zbioru skończonego. Oprócz opisu geometrycznego, grupy afiniczno-symetryczne można zdefiniować jako zbiory permutacji liczb całkowitych (..., -2, -1, 0, 1, 2, ...), które są w pewnym sensie okresowe, lub w kategoriach czysto algebraicznych jako grupa z pewnymi generatorami i relacjami . Te różne definicje pozwalają na rozszerzenie wielu ważnych właściwości skończonych grup symetrycznych na ustawienie nieskończone i są badane w ramach dziedzin kombinatoryki i teorii reprezentacji .

Definicje

Grupa afiniczno-symetryczna może być równoważnie zdefiniowana jako grupa abstrakcyjna przez generatory i relacje lub w kategoriach konkretnych modeli geometrycznych i kombinatorycznych.

Definicja algebraiczna

Diagramy Dynkina dla afiniczno-symetrycznych grup na 2 i więcej niż 2 generatorach

Jednym ze sposobów definiowania grup są generatory i relacje . W tego typu definicji generatory są podzbiorem elementów grupy, które po połączeniu dają wszystkie inne elementy. Relacje definicji to układ równań spełnianych przez te elementy, które implikują wszystkie inne równania, które spełniają. W ten sposób grupa afiniczno-symetryczna jest generowana przez zbiór ${\ Displaystyle {\ Widetilde {S}} _ {n}}$

$${\displaystyle s_{0},s_{1},\ldots,s_{n-1}}$$

${\displaystyle n\geq 3}$

1. ${\displaystyle s_{i}^{2}=1}$(generatory to inwolucje ),
2. ${\ Displaystyle s_ {i} s_ {j} = s_ {j} s_ {i}}$jeśli j nie jest jednym z , co wskazuje, że dla tych par generatorów operacja grupowa jest przemienna i${\displaystyle i-1,i,i+1}$
3. ${\ Displaystyle s_ {i} s_ {i + 1} s_ {i} = s_ {i + 1} s_ {i} s_ {i + 1}}$.

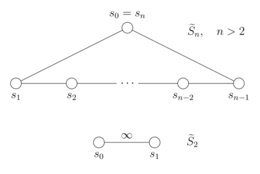
W powyższych relacjach indeksy są przyjmowane modulo n , tak że trzecia relacja obejmuje jako szczególny przypadek . (Druga i trzecia relacja są czasami nazywane relacjami warkocza .) Kiedy , grupa afiniczno-symetryczna jest nieskończoną grupą dwuścienną generowaną przez dwa elementy podlegające tylko relacjom . ${\displaystyle s_{0}s_{n-1}s_{0}=s_{n-1}s_{0}s_{n-1}}$${\displaystyle n=2}$${\displaystyle {\widetilde {S}}_{2}}$${\displaystyle s_{0},s_{1}}$${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$

Relacje te można przepisać w specjalnej formie, która definiuje grupy Coxetera , więc grupy afiniczno-symetryczne są grupami Coxetera, z ich zbiorami generującymi Coxetera. Dla The schemat Coxeter-Dynkin od jest n -cycle, podczas gdy składa się ona z dwóch węzłów połączonych krawędzi oznaczonej . Na tych diagramach wierzchołki reprezentują generatory, które dla grup Coxetera muszą być inwolucjami. Krawędzie cyklu odpowiadają relacjom między parami kolejnych generatorów, natomiast brak krawędzi między innymi parami generatorów wskazuje na ich dojazd. ${\displaystyle s_{i}}$${\displaystyle n\geq 3}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle n=2}$${\displaystyle \infty}$

Definicja geometryczna

Gdy n = 3 , przestrzeń V jest dwuwymiarową płaszczyzną, a odbicia przebiegają w poprzek linii. Punkty sieci korzeniowej typu A są zakreślone.

W przestrzeni euklidesowej o współrzędnych , zbiór punktów V, dla których tworzy (hiper)płaszczyznę , podprzestrzeń ( n − 1) -wymiarową. Dla każdej pary różnych pierwiastków ı i j o i każdej liczby całkowitej K , zestaw punktów V , które spełniają tworzy się ( n - 2) wymiarową podprzestrzeni w V i jest unikalny odbicie od V , która rozwiązuje ten podprzestrzeni. Wtedy grupa afiniczno-symetryczna może być zrealizowana geometrycznie jako zbiór map od V do samej siebie, kompozycji tych odbić. ${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle (x_ {1}, \ ldots, x_ {n})}$${\ Displaystyle x_ {1} + x_ {2} + \ ldots + x_ {n} = 0}$${\displaystyle \{1,\ldots,n\}}$${\ Displaystyle x_ {i}-x_ {j} = k}$

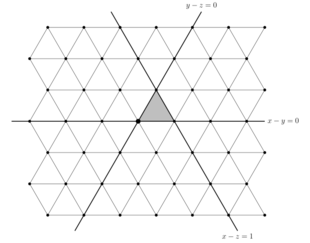
Wewnątrz V , podzbiór punktów o współrzędnych całkowitych tworzy sieć główną typu A , Λ . Jest to zbiór wszystkich wektorów całkowitych, takich jak . Każde odbicie zachowuje tę siatkę, a więc sieć jest zachowywana przez całą grupę. W rzeczywistości, można określić jako grupę sztywnych przemian z V , które zachowania siatki X . ${\ Displaystyle (a_ {1}, \ ldots, a_ {n})}$${\ Displaystyle a_ {1} + \ ldots + a_ {n} = 0}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$

Ustalone podprzestrzenie tych odbić podzielić V do przystających simplices , zwanych wnęk . Sytuacja, w której pokazano na rysunku; w tym przypadku krata korzeniowa jest kratą trójkątną, z odbijającymi liniami dzielącymi ją na wnęki w kształcie trójkąta równobocznego. Jednak w przypadku większych wymiarów wnęki nie są zwykłymi prostotą. ${\displaystyle n=3}$

Refleksje i wnęki dla grupy afiniczno-symetrycznej. Podstawowa alkowa jest zacieniona.

Aby dokonać translacji między definicjami geometrycznymi i algebraicznymi, ustaw wnękę i rozważ n hiperpłaszczyzn, które tworzą jej granicę. Odbicia przez te hiperpłaszczyzny graniczne mogą być identyfikowane z generatorami Coxetera. W szczególności istnieje unikalna alkowa (alkowa podstawowa ) składająca się z takich punktów , że , która jest ograniczona przez hiperpłaszczyzny , , ... i , zilustrowane w przypadku . Za , jeden może identyfikować poprzez odbicie z generatorem Coxeter , a także zidentyfikować poprzez odbicie z generatorem . ${\ Displaystyle (x_ {1}, \ ldots, x_ {n})}$${\ Displaystyle x_ {1} \ geq x_ {2} \ geq \ kropki \ geq x_ {n} \ geq x_ {1}-1}$${\displaystyle x_{1}-x_{2}=0}$${\displaystyle x_{2}-x_{3}=0}$${\displaystyle x_{1}-x_{n}=1}$${\displaystyle n=3}$${\displaystyle i=1,\ldots,n-1}$${\ Displaystyle x_ {i} -x_ {i + 1} = 0}$${\displaystyle s_{i}}$${\displaystyle x_{1}-x_{n}=1}$${\displaystyle s_{0}=s_{n}}$

Definicja kombinatoryczna

Elementy afinicznej grupy symetrycznej mogą być realizowane jako grupa okresowych permutacji liczb całkowitych. W szczególności powiedzmy, że funkcja jest permutacją afiniczną, jeśli ${\ Displaystyle u \ dwukropek \ mathbb {Z} \ do \ mathbb {Z}}$

• jest to bijekcja (każda liczba całkowita występuje jako wartość dokładnie jednego ),${\ Displaystyle u (x)}$${\displaystyle x}$
• ${\ Displaystyle u (x + n) = u (x) + n}$dla wszystkich liczb całkowitych x (funkcja jest ekwiwariantna przy przesunięciu o ), oraz${\ Displaystyle n}$
• ${\ Displaystyle u (1) + u (2) + \ ldots + u (n) = 1 + 2 + \ ldots + n}$, th trójkątna liczba .${\ Displaystyle n}$

Dla każdej permutacji afinicznej, a ogólniej dla każdej bijekcji równoważnika przesunięcia, wszystkie liczby muszą być odrębnymi modulo n . Permutacja afiniczna jest jednoznacznie określona przez jej notację okna , ponieważ wszystkie inne wartości można znaleźć, przesuwając te wartości. Zatem permutacje afiniczne mogą być również identyfikowane z krotkami liczb całkowitych, które zawierają jeden element z każdej klasy kongruencji modulo n i suma do . ${\displaystyle u(1),\ldots,u(n)}$ ${\displaystyle [u(1),\ldots,u(n)]}$${\ Displaystyle u}$${\displaystyle [u(1),\ldots,u(n)]}$${\displaystyle 1+2+\ldots+n}$

Aby przetłumaczyć między definicjami kombinatorycznymi i algebraicznymi, można zidentyfikować generator Coxetera z permutacją afiniczną, która ma notację okienkową , a także zidentyfikować generator z permutacją afiniczną . Mówiąc bardziej ogólnie, każde odbicie (czyli sprzężenie jednego z generatorów Coxetera) można jednoznacznie opisać w następujący sposób: dla różnych liczb całkowitych i , j in oraz dowolnej liczby całkowitej k , odwzorowuje i na j − kn , odwzorowuje j na i + kn i naprawia wszystkie dane wejściowe niezgodne z i lub j modulo n . (Pod względem definicji geometrycznej odpowiada to odbiciu w poprzek płaszczyzny . Zależność między reprezentacjami geometrycznymi i kombinatorycznymi dla innych elementów omówiono w § Połączenie między definicjami geometrycznymi i kombinatorycznymi .) ${\displaystyle i=1,\ldots,n-1}$${\displaystyle s_{i}}$${\displaystyle [1,2,\ldots,i-1,i+1,i,i+2,\ldots,n]}$${\displaystyle s_{0}=s_{n}}$${\displaystyle [0,2,3,\ldots,n-2,n-1,n+1]}$${\displaystyle \{1,\ldots,n\}}$${\ Displaystyle x_ {i}-x_ {j} = k}$

Reprezentacja jako macierze

${\displaystyle {\begin {array}{ccc|ccc|ccc}&\pocisk &&&&&&\\&&&&&&&&&\\&&&\pocisk \\hline &&&&&&&\bullet &\\&&&&&\bullet &&&\end{array}}}$

Reprezentacja macierzowa

Permutacje afiniczne można przedstawić jako nieskończone macierze permutacji okresowych . Jeśli jest permutacją afiniczną, umieszcza się wpis 1 na pozycji w nieskończonej siatce dla każdej liczby całkowitej i , a wszystkie inne wpisy są równe 0. Ponieważ u jest bijekcją, wynikowa macierz zawiera dokładnie jeden 1 w każdym wierszu i kolumnie. Warunek okresowości na mapie u zapewnia, że ​​wpis na pozycji jest równy wpisowi na pozycji dla każdej pary liczb całkowitych . Na przykład, część macierzy dla permutacji afinicznej jest pokazana na rysunku, z konwencją, w której jedynki są zastępowane przez •, zera są pomijane, numery rzędów rosną od góry do dołu, numery kolumn rosną od lewej do prawej, a granica z pola składającego się z wierszy i kolumn 1, 2, 3 jest rysowany. ${\ Displaystyle u: \ mathbb {Z} \ do \ mathbb {Z}}$${\displaystyle (ja,u(i))}$${\ Displaystyle \ mathbb {Z} \ razy \ mathbb {Z}}$${\ Displaystyle (a, b)}$${\ Displaystyle (a + n, b + n)}$${\ Displaystyle (a, b)}$${\displaystyle [2,0,4]\in {\widetilde {S}}_{3}}$

Związek ze skończoną grupą symetryczną

Grupa afinosymetryczna zawiera skończoną symetryczną grupę permutacji na elementach zarówno jako podgrupę, jak i grupę ilorazową . ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$${\ Displaystyle n}$

Jako podgrupa

Istnieje kanoniczny sposób wyboru podgrupy, która jest izomorficzna z grupą skończenie symetryczną . Z punktu widzenia definicji algebraicznej jest to podgrupa generowanych przez (z wyłączeniem prostego odbicia ). Geometrycznie odpowiada to podgrupie przekształceń, które ustalają źródło, natomiast kombinatorycznie odpowiada notacji okienka, dla której (to znaczy, w której notacja okienka jest jednowierszową notacją permutacji skończonej). ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle s_{1},\ldots,s_{n-1}}$${\displaystyle s_{0}=s_{n}}$${\ Displaystyle \ {u (1), \ ldots, u (n) \} = \ {1,2, \ ldots, n \}}$

Jeżeli jest notacją okienkową elementu tej standardowej kopii , to jego działanie na hiperpłaszczyznę V in jest określone przez permutację współrzędnych: . (W tym artykule geometryczne działanie permutacji i permutacji afinicznych jest po prawej stronie; jeśli więc u i v są dwiema permutacjami afinicznymi, działanie uv na punkt jest określone przez zastosowanie najpierw u , a następnie v .) ${\displaystyle u=[u(1),u(2),\ldots,u(n)]}$${\ Displaystyle S_ {n} \ podzbiór {\ widetilde {S}} _ {n}}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle (x_ {1}, x_ {2}, \ ldots, x_ {n}) \ cdot u = (x_ {u (1)}, x_ {u (2)}, \ ldots, x_ {u ( n)})}$

Istnieje również wiele niestandardowych kopii zawartych w . Geometryczne konstrukcja jest, aby wybrać dowolny punkt A w X (Oznacza to, że całkowita suma wektorów, których współrzędne 0); podgrupa z izometrii mocujące jest izomorficzna . Analogiczna konstrukcja jest kombinatoryczną wybrać dowolny podzbiór A z , która zawiera jeden element z każdej modulo klasa sprzężoności n i którego elementy sumują się do ; podgrupa o o afinicznych permutacji ustabilizowanie A jest izomorficzny . ${\displaystyle S_{n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) _ {a}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$${\ Displaystyle \ mathbb {Z}}$${\displaystyle 1+2+\ldots+n}$${\ Displaystyle ({\ Widetilde {S}} _ {n}) _ {A}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$

Jako iloraz

Istnieje proste odwzorowanie (technicznie rzecz biorąc homomorfizm grupy surjektywnej ) π z na skończoną grupę symetryczną . Z punktu widzenia definicji kombinatorycznej, afiniczna permutacja może być odwzorowana na permutację poprzez zredukowanie wpisów okna modulo n do elementów , pozostawiając jednowierszową notację permutacji. Obraz o afinicznej permutacji u nazywamy bazowy permutacji z u . ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$${\displaystyle \{1,2,\ldots,n\}}$${\ Displaystyle \ pi (u)}$

Mapa π wysyła generator Coxeter do permutacji którego notacja jedna linia i notacja cyklu są i , odpowiednio. W odniesieniu do generatorów Coxetera , można to zapisać jako${\displaystyle s_{0}=[0,2,3,4,\ldots,n-2,n-1,n+1]}$${\displaystyle [n,2,3,4,\ldots,n-2,n-1,1]}$${\displaystyle (1\;n)}$${\displaystyle S_{n}}$${\ Displaystyle \ pi (s_ {0}) = s_ {1} s_ {2} \ cdots s_ {n-2} s_ {n-1} s_ {n-2} \ cdots s_ {2} s_ {1} .}$

Jądro z Õ jest z definicji zbiór afinicznych permutacji których współistniejące permutacji jest tożsamość . Notacje okienek takich permutacji afinicznych mają postać , gdzie jest wektorem całkowitym takim, że , czyli gdzie . Geometrycznie to jądro składa się z translacji , czyli izometrii, które przesuwają całą przestrzeń V bez jej obracania lub odbijania. W nadużyciu notacji symbol Λ jest używany w tym artykule dla wszystkich trzech z tych zestawów (wektory całkowite w V , permutacje afiniczne z podstawową permutacją tożsamości i translacje); we wszystkich trzech ustawieniach operacja na grupie naturalnej zamienia Λ w grupę abelową generowaną swobodnie przez n − 1 wektorów . ${\ Displaystyle [1-a_ {1} \ cdot n, 2-a_ {2} \ cdot n, \ ldots, n-a_ {n} \ cdot n]}$${\displaystyle (a_{1},a_{2},\ldots,a_{n})}$${\displaystyle a_{1}+a_{2}+\ldots+a_{n}=0}$${\ Displaystyle (a_ {1}, \ ldots, a_ {n}) \ w \ Lambda}$${\displaystyle \{(1,-1,0,\ldots,0),(0,1,-1,\ldots,0),\ldots,(0,\ldots,0,1,-1)\ }}$

Związek między jądrem, grupą afiniczno-symetryczną i obrazem π można wyrazić krótkim ciągiem ścisłym . Oto jądro, wolna grupa abelowa z n − 1 generatorami. ${\ Displaystyle 0 \ do \ mathbb {Z} ^ {n-1} \ do {\ widetilde {S}} _ {n} \ mathop {\ przesłonięty {\ pi} {\ do}} S_ {n} \ do 0}$${\ Displaystyle \ mathbb {Z} ^ {n-1} \ cong \ Lambda}$

Związek między definicjami geometrycznymi i kombinatorycznymi

Wnęki do znakowania przez permutacje afiniczne. Wnęka A jest oznaczona notacją okna dla permutacji u, jeśli u wysyła podstawową alkowę (zacieniowaną) do A . Liczby ujemne są oznaczone overbarami.${\displaystyle {\widetilde {S}}_{3}}$

Afiniczna grupa symetryczna ma Λ jako normalną podgrupę i jest izomorficzna z produktem półbezpośrednim${\ Displaystyle {\ Widetilde {S}} _ {n}}$

$${\ Displaystyle {\ widetilde {S}} _ {n} \ cong S_ {n} \ ltimes \ Lambda}$$

o posiada unikalny realizacji jako produktu , gdy jest to permutacje w standardzie kopii w i jest tłumaczenie na język . ${\displaystyle S_{n}}$${\displaystyle S_{n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle u=r\cdot t}$${\ Displaystyle r}$${\displaystyle S_{n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle t}$${\ Displaystyle \ Lambda}$

Ten punkt widzenia pozwala na bezpośrednią translację pomiędzy kombinatoryczną i geometryczną definicją : jeśli napiszemy gdzie i wtedy permutacja afiniczna

zdefiniowanemu przez ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle [u (1), \ ldots, u (n)] = [r_ {1}-a_ {1} \ cdot n, \ ldots, r_ {n} -a_ {n} \ cdot n]}$${\ Displaystyle r = [r_ {1}, \ ldots, r_ {n}] = \ pi (u)}$${\ Displaystyle (a_ {1}, a_ {2}, \ ldots, a_ {n}) \ w \ Lambda}$

$${\ Displaystyle (x_ {1}, \ ldots, x_ {n}) \ cdot u = \ lewo (x_ {r (1)} + a_ {1}, \ ldots, x_ {r (n)} + a_ { n}\prawo).}$$

Ponadto, jak w przypadku każdej afinicznej grupy Coxetera, grupa afiniczno-symetryczna działa przechodnie i swobodnie na zbiór wnęk: dla każdych dwóch wnęk unikalny element grupy przenosi jedną wnękę do drugiej. Stąd, poprzez dowolny wybór wnęce , można to grupy w jeden-do-jednego odpowiednio do wnęk: THE

. Ta identyfikacja jest zilustrowana po prawej stronie. ${\displaystyle A_{0}}$${\displaystyle A_{0}}$${\ Displaystyle A = A_ {0}\ cdot g}$${\displaystyle A_{0}}$${\displaystyle {\widetilde {S}}_{3}}$

Przykład: n = 2

Grupa afiniczno-symetryczna działa na linii V w płaszczyźnie euklidesowej. Odbicia są przez linie przerywane. Zaznaczono wektory sieci korzeniowej Λ .${\displaystyle {\widetilde {S}}_{2}}$

Algebraicznie jest

, generowaną przez dwa generatory podlegające relacjom . Każdy inny element grupy można zapisać jako naprzemienny produkt kopii i . ${\displaystyle {\widetilde {S}}_{2}}$${\displaystyle s_{0},s_{1}}$${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$${\displaystyle s_{0}}$${\displaystyle s_{1}}$

Kombinatorycznie permutacja afiniczna ma notację okienkową , odpowiadającą bijekcji dla każdej liczby całkowitej

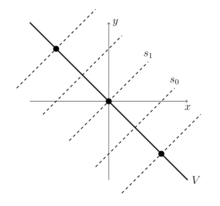
. Inne elementy mają następujące notacje okienne: ${\displaystyle s_{1}}$${\displaystyle [2,1]}$${\displaystyle 2k\mapsto 2k-1,2k-1\mapsto 2k}$${\displaystyle s_{0}}$${\ Displaystyle [0,3]}$${\displaystyle 2k\mapsto 2k+1,2k+1\mapsto 2k}$

• ${\ Displaystyle \ overbrace {s_ {0}s_ {1} \ cdots s_ {0} s_ {1}} ^ {2 k \, {\ tekst {czynniki}}} = [1+2k,2-2k],}$
• ${\ Displaystyle \ overbrace {s_ {1} s_ {0} \ cdots s_ {1} s_ {0}} ^ {2 k \ {\ tekst {czynniki}}} = [1-2 k, 2 + 2 k],}$
• ${\ Displaystyle \ overbrace {s_ {0}s_ {1} \ cdots s_ {0}} ^ {2k + 1 \, {\ tekst {czynniki}}} = [2 + 2 k, 1-2 k],}$
• ${\ Displaystyle \ overbrace {s_ {1} s_ {0} \ cdots s_ {1}} ^ {2k + 1 \ {\ tekst {czynniki}}} = [2-2 (k + 1), 1 + 2 (k+1)].}$

Geometrycznie przestrzeń V jest prostą z równaniem na płaszczyźnie euklidesowej . Sieć główna wewnątrz

. ${\displaystyle x+y=0}$${\ Displaystyle \ mathbb {R} ^ {2}}$${\displaystyle (a,-a)}$${\displaystyle s_{1}}$${\displaystyle x=y}$${\displaystyle s_{0}}$${\displaystyle x=y+1}$${\ Displaystyle \ lewo ({\ tfrac {1} {2}}, - {\ tfrac {1} {2}} \ po prawej)}$${\ Displaystyle \ mathbb {R} ^ {1}}$${\displaystyle (x,-x)}$${\ Displaystyle (s_{1}s_{0}) ^ {k}}$${\displaystyle s_{1}(s_{0}s_{1})^{k}}$

Statystyki permutacji i wzorce permutacji

Wiele statystyk permutacyjnych i innych cech kombinatoryki permutacji skończonych można rozszerzyć na przypadek afiniczny.

Zjazdy, długość i inwersje

Długość elementu

. ${\ Displaystyle \ ell (g)}$${\ Displaystyle g = s_ {i_ {1}} \ cdots s_ {i_ {k}}}$

Geometrycznie długość elementu g w to liczba odzwierciedla hiperplaszczyzn dzielące i , gdzie jest podstawowym nisza (simplex ograniczony odbijających hiperplaszczyzn generatorów Coxeter ). (W rzeczywistości to samo dotyczy każdej grupy Coxetera o powinowactwie.) ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle A_{0}}$${\displaystyle A_{0}\cdot g}$${\displaystyle A_{0}}$${\displaystyle s_{0},s_{1},\ldots,s_{n-1}}$

Kombinatorycznie, długość permutacji afinicznej jest zakodowana w postaci odpowiedniego pojęcia inwersji . W szczególności istnieje permutacja afiniczna u, która

$${\ Displaystyle \ ell (u) = \ # \ lewo \ {(i, j) \ dwukropek i \ w \ {1, \ ldots, n \}, i < j, {\ tekst { i}} u (i ))>u(j)\prawo\}.}$$

Alternatywnie jest to liczba klas równoważności par takich, że i pod relacją równoważności, jeśli dla pewnej liczby całkowitej

. ${\ Displaystyle (i, j) \ w \ mathbb {Z} \ razy \ mathbb {Z}}$${\displaystyle i<j}$${\displaystyle u(i)>u(j)}$${\displaystyle (i,j)\equiv (i',j')}$${\displaystyle (i-i',j-j')=(kn,kn)}$

Funkcja generująca długość w is ${\ Displaystyle {\ Widetilde {S}} _ {n}}$

$${\ Displaystyle \ suma _ {g \ w {\ widetilde {S}} _ {n}} q ^ {\ ell (g)} = {\ Frac {1-q ^ {n}} {(1-q) ^{n}}}.}$$

Podobnie można zdefiniować afiniczny analog zstępów w permutacjach: powiedzmy, że afiniczna permutacja u ma zstąpienie w pozycji i, jeśli . (Przez okresowość

.) ${\displaystyle u(i)>u(i+1)}$${\displaystyle i+kn}$

Algebraicznie, spadki odpowiadają właściwym spadkom w sensie grup Coxetera; to znaczy, i jest pochodzeniem u wtedy i tylko wtedy, gdy . Zjazdy lewostronne (czyli te indeksy

w ciągu . ${\ Displaystyle \ ell (u \ cdot s_ {i}) <\ ell (u)}$${\ Displaystyle \ ell (s_ {i} \ cdot u) <\ ell (u)}$${\ Displaystyle u ^ {-1}}$ ${\ Displaystyle \ ldots, u (-2), u (-1), u (0), u (1), u (2), \ ldots }$

Geometrycznie i jest spadkiem u wtedy i tylko wtedy, gdy stała hiperpłaszczyzna oddziela wnęki i . ${\displaystyle s_{i}}$${\displaystyle A_{0}}$${\displaystyle A_{0}\cdot u}$

Ponieważ istnieje tylko skończenie wiele możliwości dla liczby zejść permutacji afinicznej, ale nieskończenie wiele permutacji afinicznych, nie jest możliwe naiwne utworzenie funkcji generującej dla permutacji afinicznych przez liczbę zstępów (analog afiniczny wielomianów Eulera ). Jednym z możliwych rozwiązań jest rozważenie spadków afinicznych (równoważnie spadków cyklicznych) w grupie skończenie symetrycznej . Innym jest równoczesne rozważenie długości i liczby zstępów permutacji afinicznej. Funkcja generująca dla tych statystyk jednocześnie dla wszystkich

to ${\displaystyle S_{n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$

$${\ Displaystyle \ suma _ {n \ geq 1} {\ Frac {x ^ {n}} {1-q ^ {n}}} \ suma _ {w \ w {\ widetilde {S}} _ {n} }t^{\nazwa operatora {des} (w)}q^{\ell (w)}=\left[{\frac {x\cdot {\frac {\częściowy }{\częściowy {x}}}\log (\exp(x;q))}{1-t\exp(x;q)}}\right]_{x\mapsto x{\frac {1-t}{1-q}}}}$$

gdzie des( w ) jest liczbą zejść permutacji afinicznej w i jest

. ${\ Displaystyle \ exp (x; q) = \ suma _ {n \ geq 0} {\ Frac {x ^ {n} (1-q) ^ {n}} {(1-q) (1-q ^ {2})\cdots (1-q^{n})}}}$

Typ cyklu i długość odbicia

Dowolna bijekcja dzieli liczby całkowite na (prawdopodobnie nieskończoną) listę (prawdopodobnie nieskończonych) cykli: dla każdej liczby całkowitej

jest sekwencją, w której potęgowanie reprezentuje kompozycję funkcjonalną. Na przykład permutacja afiniczna w notacji okienkowej zawiera dwa nieskończone cykle oraz nieskończenie wiele skończonych cykli dla każdego . Cykle permutacji afinicznej w oczywisty sposób odpowiadają cyklom podstawowej permutacji: w powyższym przykładzie, z podstawową permutacją , pierwszy nieskończony cykl odpowiada cyklowi (1), drugi odpowiada cyklowi (45), a wszystkie cykle skończone odpowiadają cyklowi (23). ${\ Displaystyle u: \ mathbb {Z} \ do \ mathbb {Z}}$${\ Displaystyle (\ ldots, u ^ {-2} (i), u ^ {-1} (i), ja, u (i), u ^ {2} (i), \ ldots )}$${\ Displaystyle {\ Widetilde {S}} _ {5}}$${\ Displaystyle [6,3,2,0,4]}$${\displaystyle (\ldots,-9,-4,1,6,11,\ldots)}$${\displaystyle (\ldots,10,9,5,4,0,-1,-5\ldots)}$${\ Displaystyle (5k + 2,5k + 3)}$${\ Displaystyle k \ w \ mathbb {Z}}$${\ Displaystyle [1,3,2,5,4] = (1) (23) (45)}$

Dla permutacji afinicznej u , następujące warunki są równoważne: wszystkie cykle u są skończone, u ma skończony porządek , a geometryczne oddziaływanie u na przestrzeń V ma co najmniej jeden stały punkt.

Długość odbicie elementu

wynosi ${\ Displaystyle \ell _ {R} (u)}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle r_{1},\ldots,r_{k}}$${\displaystyle u=r_{1}\cdots r_{k}}$${\displaystyle nc(u)}$${\displaystyle c(u)}$${\displaystyle [5,2,0,3]}$ ${\ Displaystyle \ nu (u)}$${\ Displaystyle (1,-1,0)}$${\ Displaystyle (1,-1), (0)}$

$${\ Displaystyle \ ell _ {R} (u) = n-2 \ nu (u) + c (\ pi (u)),}$$

gdzie jest podstawowa permutacja

. ${\ Displaystyle \ pi (u)}$

Dla każdego afinicznej permutacji U , jest wybór podgrupy W w taki sposób, że , i dla standardowej postaci obserwowaną tym iloczynów produktu trzeba . ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle W \ cong S_ {n}}$${\ Displaystyle {\ Widetilde {S}} _ {n} = W \ ltimes \ Lambda}$${\displaystyle u=w\cdot t}$${\ Displaystyle \ ell _ {R} (u) = \ ell _ {R} (w) + \ ell _ {R} (t)}$

Elementy w pełni przemienne i unikanie wzorców

Zmniejszona słowo dla elementu g grupy Coxeter jest krotką z Coxeter generatorów minimalnej możliwej długości takiej . Element

jeśli można przekształcić dowolne zredukowane słowo w dowolne inne poprzez sekwencyjną zamianę par czynników, które przechodzą. Na przykład w skończonej grupie symetrycznej element jest w pełni przemienny, ponieważ jego dwa zredukowane słowa i mogą być połączone przez zamianę czynników przemiennych , ale nie jest w pełni przemienny, ponieważ nie ma możliwości osiągnięcia zredukowanego słowa zaczynając od zredukowanego słowa przez dojazdy. ${\ Displaystyle (s_ {i_ {1}}, \ ldots, s_ {i_ {\ ell (g)}})}$${\ Displaystyle g = s_ {i_ {1}} \ cdots s_ {i_ {\ ell (g)}}}$${\displaystyle S_{4}}$${\ Displaystyle 2143 = (12) (34)}$${\displaystyle (s_{1},s_{3})}$${\displaystyle (s_{3},s_{1})}$${\ Displaystyle 3214 = (13) (2) (4)}$${\displaystyle (s_{2},s_{1},s_{2})}$${\displaystyle (s_{1},s_{2},s_{1})}$

Billy, Jockusch i Stanley (1993) wykazali, że w skończonej grupie symetrycznej permutacja jest w pełni przemienna wtedy i tylko wtedy, gdy unika

jest w pełni przemienna wtedy i tylko wtedy, gdy nie istnieją liczby całkowite takie, że . ${\displaystyle S_{n}}$${\displaystyle i<j<k}$${\displaystyle u(i)>u(j)>u(k)}$

Liczba permutacji afinicznych unikających pojedynczego wzorca p jest skończona wtedy i tylko wtedy, gdy p unika wzorca 321, a więc w szczególności istnieje nieskończenie wiele w pełni przemiennych permutacji afinicznych. Zostały one wymienione według długości w ( Hanusa & Jones 2010 ).

Podgrupy paraboliczne i inne struktury

Podgrupy paraboliczne i ich przedstawiciele coset oferują bogatą strukturę kombinatoryczną. Inne aspekty afiniczno-symetrycznej grupy, takie jak jej porządek Bruhata i teoria reprezentacji, można również zrozumieć za pomocą modeli kombinatorycznych. ${\ Displaystyle {\ Widetilde {S}} _ {n}}$

Podgrupy paraboliczne, przedstawiciele coset

Liczydło permutacji afinicznej [−5, 0, 6, 9].

Średnia paraboliczny podgrupa grupy Coxeter jest podgrupą wytwarzany przez część jego prądotwórczego Coxeter. Maksymalne podgrupy paraboliczne to te, które pochodzą z pominięcia pojedynczego generatora Coxetera. W , wszystkie maksymalne podgrupy paraboliczne są izomorficzne z grupą skończenie symetryczną . Podgrupa generowana przez podzbiór składa się z tych permutacji afinicznych, które stabilizują przedział , to znaczy odwzorowują każdy element tego przedziału na inny element przedziału. ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$${\ Displaystyle \ {s_{0}, \ ldots, s_ {n-1} \} \ smallsetminus \ {s_ {i} \}}$${\displaystyle [i+1,i+n]}$

Niemaksymalne podgrupy paraboliczne są wszystkie izomorficzne z podgrupami parabolicznymi , to znaczy z

. ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle S_{n}}$ ${\ Displaystyle S_ {a_ {1}} \ razy \ cdots \ razy S_ {a_ {k}}}$${\displaystyle a_{1},\ldots,a_{k}}$

Dla ustalonego elementu i z , niech będzie maksymalnym właściwym podzbiorem generatorów Coxetera pomijając , i niech oznacza podgrupę paraboliczną generowaną przez

posiada unikalny element o minimalnej długości. Zbiór takich przedstawicieli, oznaczony jako , składa się z następujących permutacji afinicznych: ${\ Displaystyle \ {0, \ ldots, n-1 \}}$${\ Displaystyle J = \ {s_ {0}, \ ldots, s_ {n-1} \} \ smallsetminus \ {s_ {i} \}}$${\displaystyle s_{i}}$${\ Displaystyle ({\ Widetilde {S}} _ {n}) _ {J}}$ ${\ Displaystyle g \ cdot ({\ widetilde {S}} _ {n}) _ {J}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) ^ {J}}$

$${\ Displaystyle ({\ widetilde {S}} _ {n}) ^ {J} = \ lewo \ {u \ w {\ widetilde {S}} _ {n} \ okrężnica u (i-n + 1) < u(i-n+2)<\ldots <u(i-1)<u(i)\prawo\}.}$$

W szczególnym przypadku, gdy , a więc jest to standardowa kopia inside , elementy mogą być naturalnie reprezentowane przez

, rosnącym kolejno wzdłuż rzędów, a następnie od góry do dołu; liczby całkowite są zakreślone, jeśli leżą bezpośrednio nad jednym z wpisów okna przedstawiciela minimalnego coset. Na przykład minimalny przedstawiciel coset jest reprezentowany przez diagram liczydła po prawej stronie. Aby obliczyć długość reprezentanta z diagramu liczydła, dodaje się liczbę nie zakreślonych liczb, które są mniejsze niż ostatni zakreślony wpis w każdej kolumnie. (W pokazanym przykładzie daje to .) ${\ Displaystyle J = \ {s_ {1}, \ ldots, s_ {n-1} \}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) _ {J} \ cong S_ {n}}$${\displaystyle S_{n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) ^ {J} \ cong {\ widetilde {S}} _ {n} / S_ {n}}$${\displaystyle u=[-5,0,6,9]}$${\ Displaystyle 5 + 3 + 0 + 1 = 9}$

Inne modele kombinatoryczne reprezentantów coset o minimalnej długości mogą być podane w kategoriach

. ${\ Displaystyle {\ Widetilde {S}} _ {n} / S_ {n}}$${\ Displaystyle {\ Widetilde {S}} _ {n} / S_ {n}}$

Zamówienie Bruhata

Zamówienie G. Bruhat na ma następującą realizację kombinatorycznej. Jeśli

. ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle u[i,j]}$${\displaystyle a\leq i}$${\displaystyle u(a)\geq j}$${\displaystyle u=[2,0,4]\in {\widetilde {S}}_{3}}$${\displaystyle u[3,1]=3}$${\ Displaystyle a = 0,1,3}$${\displaystyle u\leq v}$${\displaystyle u[i,j]\leq v[i,j]}$

Teoria reprezentacji i afiniczna korespondencja Robinsona–Schensteda

W skończonej grupy symetrycznego korespondencji Robinson-Schensted daje bijection między grupą a pary o

. ${\ Displaystyle (P, Q)}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle (P, Q, \ rho )}$

Realizacje odwrotne

Wnęki do etykietowania przez permutacje afiniczne, odwrotność do etykietowania powyżej.${\displaystyle {\widetilde {S}}_{3}}$

W niektórych sytuacjach można rozważyć działanie afiniczno-symetrycznej grupy na lub na wnękach, które jest odwrotne do podanego powyżej. Opisujemy teraz te alternatywne realizacje. ${\ Displaystyle \ mathbb {Z}}$

W kombinatorycznym działaniu on generator działa poprzez przełączanie

formy permutacji.) ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle \ mathbb {Z}}$${\displaystyle s_{i}}$ ${\displaystyle S_{n}}$

W geometrycznym działaniu , generator działa na alkowę

. ${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\displaystyle s_{i}}$

Związek z innymi obiektami matematycznymi

Grupa afiniczno-symetryczna jest blisko spokrewniona z wieloma innymi obiektami matematycznymi.

Żonglowanie wzorami

Wzór żonglowania 441 zwizualizowany jako diagram łukowy: wysokość każdego rzutu odpowiada długości łuku; dwa kolory węzłów to lewa i prawa ręka żonglera. Ten wzór ma cztery skrzyżowania, które powtarzają się okresowo.

Wzór żonglerki 441

W ( Ehrenborg i Readdy 1996 ) istnieje zgodność między permutacjami afinicznymi a wzorcami żonglowania zakodowanymi w wersji notacji sitewap . W tym przypadku wzorzec żonglowania okresem n jest sekwencją nieujemnych liczb całkowitych (z pewnymi ograniczeniami), która oddaje zachowanie piłek rzucanych przez żonglera, gdzie liczba wskazuje czas, jaki

funkcję określoną przez ${\ Displaystyle (a_ {1}, \ ldots, a_ {n})}$${\displaystyle a_{i}}$${\ Displaystyle b = {\ Frac {a_ {1} + \ ldots + a_ {n}} {n}}}$${\ Displaystyle {\ bf {a}} = (a_ {1}, \ ldots, a_ {n})}$${\ Displaystyle w_ {\ bf {a}} \ dwukropek \ mathbb {Z} \ do \ mathbb {Z}}$

$${\ Displaystyle w_ {\ bf {a}} (i) = ja + a_ {i}-b}$$

gdzie indeksy ciągu a są brane modulo n . Potem jest afiniczne w permutacji , a ponadto każdy affine permutacja powstaje wzorzec żonglerka w ten sposób. W ramach tej bijekcji długość permutacji afinicznej jest kodowana przez naturalną statystykę we wzorcu żonglowania: ${\displaystyle w_{\bf {a}}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$

$${\displaystyle \ell (w_{\bf {a}})=(b-1)n-\operatorname {krzyż} ({\bf {a}}),}$$

gdzie oznacza liczbę przejść (do okresowości) na schemacie łuku . Pozwala to na elementarny dowód funkcji generującej dla permutacji afinicznych według długości. ${\displaystyle \operatorname {krzyż} ({\bf {a}})}$

Na przykład wzór żonglowania 441 (pokazany po prawej) ma i . Dlatego odpowiada permutacji afinicznej . Wzorzec żonglowania ma cztery skrzyżowania, a permutacja afiniczna ma długość . ${\displaystyle n=3}$${\displaystyle b={\frac {4+4+1}{3}}=3}$${\ Displaystyle w_ {441} = [1+4-3,2+4-3,3+1-3]=[2,3,1]}$${\ Displaystyle \ ell (w_ {441}) = (3-1) \ cdot 3-4 = 2}$

Podobne techniki można zastosować do wyprowadzenia funkcji generującej dla minimalnych przedstawicieli kosetowych według długości. ${\ Displaystyle {\ Widetilde {S}} _ {n} / S_ {n}}$

Złożone grupy refleksji

W prawdziwej skończenie wymiarowej przestrzeni wewnętrznej produktu , o odbicie jest transformacja liniowa że poprawki liniowy punktowo hiperpłaszczyzna i neguje wektor prostopadły do płaszczyzny. Pojęcie to można rozszerzyć na przestrzenie wektorowe nad innymi ciałami . W szczególności w złożonej wewnętrznej przestrzeni produktu odbicie jest jednostkową transformacją T o skończonym porządku, która ustala hiperpłaszczyznę. Oznacza to, że wektory prostopadłe do hiperpłaszczyzny są wektorami własnymi T , a skojarzona wartość własna jest złożonym pierwiastkiem jedności . Złożonej grupie, odbicie jest skończoną grupy liniowych przekształceń złożonej przestrzeni wektorowej generowanego przez odbicia.

Złożone grupy refleksyjne zostały w pełni sklasyfikowane przez Shepharda i Todda (1954) : każda złożona grupa refleksyjna jest izomorficzna z produktem nieredukowalnych złożonych grup refleksyjnych, a każda nieredukowalna albo należy do nieskończonej rodziny (gdzie

tymi pierwiastkami jedności. Grupy są podgrupami , aw szczególności grupa składa się z tych macierzy, w których iloczyn niezerowych wpisów jest równy 1. ${\ Displaystyle G (m, p, n)}$${\ Displaystyle G (m, 1, n)}$ ${\ Displaystyle (\ mathbb {Z} / m \ mathbb {Z}) \ wr S_ {n}}$ ${\ Displaystyle \ mathbb {Z} / m \ mathbb {Z}}$${\displaystyle S_{n}}$${\ Displaystyle G (m, p, n)}$${\ Displaystyle G (m, 1, n)}$${\ Displaystyle G (m, m, n)}$

W ( Shi 2002 ) Shi pokazał, że grupa afiniczno-symetryczna jest rodzajową osłoną rodziny w następującym sensie: dla każdej dodatniej liczby całkowitej

w jest elementem Coxetera w . ${\ Displaystyle \ lewo \ {G (m, m, n) \ dwukropek m \ geq 1 \ prawo \}}$${\ Displaystyle \ pi _ {m}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle G (m, m, n)}$${\ Displaystyle G (m, m, n) \ twoheadrightarrow G (p, p, n)}$${\displaystyle p\mid m}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle \ pi _ {m}}$${\ Displaystyle G (m, m, n)}$${\ Displaystyle m> 1}$ ${\displaystyle s_{0}\cdot s_{1}\cdots s_{n-1}}$${\ Displaystyle {\ Widetilde {S}} _ {n}}$${\ Displaystyle G (m, m, n)}$

Algebry afinicznego Liego

Każda afiniczna grupa Coxetera jest powiązana z afiniczną algebrą Liego , pewną nieskończenie wymiarową nieskojarzeniową algebrą z niezwykle ładnymi własnościami teorii reprezentacji. W tym związku grupa Coxetera powstaje jako grupa symetrii przestrzeni pierwiastkowej algebry Liego (podwójnej podalgebry Cartana). W klasyfikacji afinicznych algebr Liego, skojarzona z nią jest typu (nieskręcona) , z