Metoda Newtona - Newton's method

W analizie numerycznej , metoda Newtona , znany również jako metoda Newtona-Raphsona , nazwany po Isaac Newton i Joseph Raphson , to algorytm korzeń rozpoznawczej , która produkuje kolejno lepszych przybliżeń do korzeni (lub zer) o rzeczywistej -valued funkcji . Najbardziej podstawowa wersja zaczyna się od funkcji jednej zmiennej f zdefiniowanej dla zmiennej rzeczywistej x , pochodnej funkcji f ′ i początkowego przypuszczenia x ₀ dla pierwiastka zf . Jeśli funkcja spełnia wystarczające założenia, a wstępne przypuszczenie jest bliskie, to

${\ Displaystyle x_ {1} = x_ {0}- {\ Frac {f (x_ {0})} {f '(x_ {0})}}}$

jest lepszym przybliżeniem pierwiastka niż x ₀ . Geometrycznie ( x ₁ , 0) jest przecięciem x -osiowy i styczna z wykresu na F w ( x ₀ , f  ( x ₀ )) , to znaczy, ulepszona przypuszczenie jest unikalnym źródłem w przybliżeniu liniowy w punkcie początkowym. Proces jest powtarzany jako

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f '(x_ {n})}}}$

aż do osiągnięcia wystarczająco dokładnej wartości. Algorytm ten jest pierwszym w klasie metod Householdera , po nim jest metoda Halleya . Metodę można również rozszerzyć na funkcje złożone i układy równań .

Opis

Funkcja f jest pokazana na niebiesko, a linia styczna na czerwono. Widzimy, że x _{n + 1} jest lepszym przybliżeniem niż x _n dla pierwiastka x funkcji f .

Pomysł polega na tym, aby zacząć od początkowego zgadywania, które jest dość bliskie rzeczywistemu pierwiastkowi, a następnie przybliżyć funkcję za pomocą jej stycznej za pomocą rachunku różniczkowego , a na końcu obliczyć przecięcie x tej prostej stycznej za pomocą algebry elementarnej . Ten znak przecięcia x będzie zwykle lepszym przybliżeniem pierwotnego korzenia funkcji niż pierwsze odgadnięcie, a metoda może być iterowana .

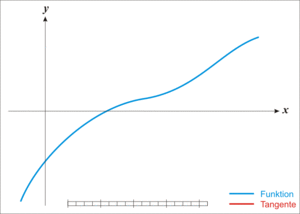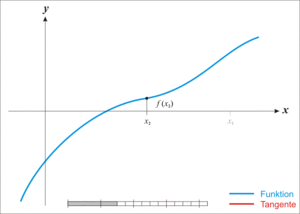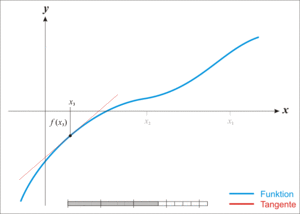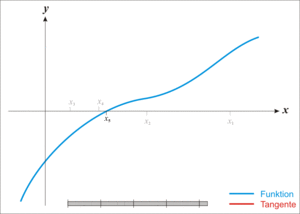
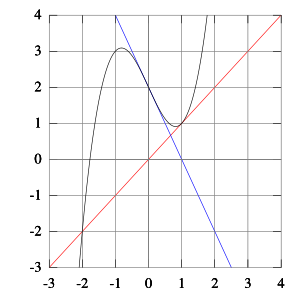
Bardziej formalnie załóżmy, że f  : ( a , b ) → ℝ jest różniczkowalną funkcją zdefiniowaną na przedziale ( a , b ) o wartościach w liczbach rzeczywistych  ℝ , i mamy pewne bieżące przybliżenie x _n . Następnie możemy wyprowadzić wzór na lepsze przybliżenie, x _{n + 1} , odwołując się do diagramu po prawej stronie. Równanie prostej stycznej do krzywej y = f  ( x ) przy x = x _n to

${\ Displaystyle y = f '(x_ {n}) \ (x-x_ {n}) + f (x_ {n})}$

gdzie f′ oznacza pochodną . Punkt przecięcia x tej prostej (wartość x, która sprawia, że y = 0 ) jest przyjmowany jako następne przybliżenie, x _{n + 1} , do pierwiastka, tak że równanie prostej stycznej jest spełnione, gdy : ${\ Displaystyle (x, y) = (x_ {n + 1}, 0)}$

${\ Displaystyle 0 = f '(x_ {n}) \ (x_ {n + 1} -x_ {n}) + f (x_ {n}).}$

Rozwiązanie dla x _{n + 1} daje

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f”(x_ {n})}}.}$

Proces zaczynamy od jakiejś dowolnej wartości początkowej x ₀ . (Im bliżej zera, tym lepiej. Ale przy braku jakiejkolwiek intuicji co do tego, gdzie może leżeć zero, metoda „zgadnij i sprawdź” może zawęzić możliwości do rozsądnie małego przedziału, odwołując się do twierdzenia o wartości pośredniej .) Metoda zwykle będzie zbieżna, pod warunkiem, że początkowe przypuszczenie jest wystarczająco bliskie nieznanego zera i że f ′ ( x ₀ ) ≠ 0 . Co więcej, dla zera o krotności  1 zbieżność jest co najmniej kwadratowa (patrz współczynnik zbieżności ) w sąsiedztwie zera, co intuicyjnie oznacza, że ​​liczba prawidłowych cyfr z grubsza podwaja się na każdym kroku. Więcej szczegółów można znaleźć w sekcji analizy poniżej.

Metody gospodarza są podobne, ale mają wyższy porządek dla jeszcze szybszej konwergencji. Jednak dodatkowe obliczenia wymagane dla każdego kroku mogą spowolnić ogólną wydajność w stosunku do metody Newtona, szczególnie jeśli ocena f lub jej pochodnych jest kosztowna obliczeniowo.

Historia

Nazwa „metoda Newtona” wywodzi się od opisu szczególnego przypadku metody przez Isaaca Newtona w De analysi per aequationes numero terminorum infinitas (napisanym w 1669 r., opublikowanym w 1711 r. przez Williama Jonesa ) oraz w De metodis fluxionum et serierum infinitarum ( napisany w 1671, przetłumaczony i opublikowany jako Method of Fluxions w 1736 przez Johna Colsona ). Jednak jego metoda różni się znacznie od nowoczesnej metody podanej powyżej. Newton zastosował tę metodę tylko do wielomianów, zaczynając od wstępnego oszacowania pierwiastka i wyodrębniając sekwencję poprawek błędów. Wykorzystał każdą poprawkę do przepisania wielomianu pod względem pozostałego błędu, a następnie rozwiązał nową poprawkę, pomijając składniki wyższego stopnia. Nie łączył wprost metody z pochodnymi ani nie przedstawił ogólnej formuły. Newton zastosował tę metodę zarówno do problemów numerycznych, jak i algebraicznych, tworząc w tym drugim przypadku szereg Taylora .

Newton mógł wyprowadzić swoją metodę z podobnej, ale mniej precyzyjnej metody Vieta . Istotę metody Viety można odnaleźć w pracy perskiego matematyka Sharafa al-Din al-Tusiego , podczas gdy jego następca Jamshīd al-Kāshī wykorzystał formę metody Newtona do rozwiązania x ^P − N = 0 w celu znalezienia pierwiastków N ( Rok 1995). Szczególny przypadek metody Newtona do obliczania pierwiastków kwadratowych był znany od czasów starożytnych i często nazywany jest metodą babilońską .

Metodę Newtona zastosował XVII-wieczny japoński matematyk Seki Kōwa do rozwiązywania równań z jedną zmienną, choć brakowało jej związku z rachunkiem różniczkowym.

Metoda Newtona została po raz pierwszy opublikowana w 1685 roku w A Treatise of Algebra, zarówno historycznym, jak i praktycznym autorstwa Johna Wallisa . W 1690 roku Joseph Raphson opublikował uproszczony opis w Analysis aequationum universalis . Raphson również zastosował tę metodę tylko do wielomianów, ale uniknął żmudnego procesu przepisywania Newtona, wyodrębniając każdą kolejną poprawkę z oryginalnego wielomianu. To pozwoliło mu wyprowadzić powtarzalne wyrażenie wielokrotnego użytku dla każdego problemu. Wreszcie w 1740 r. Thomas Simpson opisał metodę Newtona jako iteracyjną metodę rozwiązywania ogólnych równań nieliniowych za pomocą rachunku różniczkowego, zasadniczo podając powyższy opis. W tej samej publikacji Simpson podaje również uogólnienie na układy dwóch równań i zauważa, że ​​metoda Newtona może być wykorzystana do rozwiązywania problemów optymalizacyjnych poprzez ustawienie gradientu na zero.

Arthur Cayley w 1879 r. w Wyimaginowanym problemie Newtona-Fouriera jako pierwszy zauważył trudności w uogólnieniu metody Newtona na złożone pierwiastki wielomianów o stopniu większym niż 2 i złożonych wartościach początkowych. Otworzyło to drogę do badania teorii iteracji funkcji wymiernych.

Względy praktyczne

Metoda Newtona jest potężną techniką — ogólnie rzecz biorąc zbieżność jest kwadratowa: gdy metoda zbiega się na pierwiastku, różnica między pierwiastkiem a przybliżeniem jest podnoszona do kwadratu (liczba dokładnych cyfr w przybliżeniu podwaja się) na każdym kroku. Jednak z tą metodą są pewne trudności.

Trudność w obliczeniu pochodnej funkcji

Metoda Newtona wymaga, aby pochodną można było obliczyć bezpośrednio. Wyrażenie analityczne dla pochodnej może nie być łatwo dostępne lub może być kosztowne w ocenie. W takich sytuacjach może być właściwe przybliżenie pochodnej za pomocą nachylenia prostej przechodzącej przez dwa pobliskie punkty na funkcji. Użycie tego przybliżenia dałoby coś w rodzaju metody siecznych, której zbieżność jest wolniejsza niż metody Newtona.

Brak metody zbieżności do korzenia

Ważne jest, aby przejrzeć dowód zbieżności kwadratowej metody Newtona przed jej wdrożeniem. W szczególności należy przejrzeć założenia przyjęte w dowodzie. W sytuacjach, w których metoda nie jest zbieżna , dzieje się tak , ponieważ założenia przyjęte w tym dowodzie nie są spełnione.

Przeregulowanie

Jeśli pierwsza pochodna nie zachowuje się dobrze w sąsiedztwie konkretnego pierwiastka, metoda może przekroczyć i odbiegać od tego pierwiastka. Przykładem funkcji z jednym pierwiastkiem, dla której pochodna nie zachowuje się dobrze w sąsiedztwie pierwiastka, jest

${\ Displaystyle f (x) = | x | ^ {a} \ quad 0 < a < {\ tfrac {1} {2}}}$

dla którego pierwiastek zostanie przekroczony, a ciąg x będzie rozbieżny. Dla a = 1/2, korzeń nadal będzie przestrzelony, ale sekwencja będzie oscylować między dwiema wartościami. Do1/2< a < 1 , korzeń nadal będzie przestrzelony, ale sekwencja będzie zbieżna, a dla a ≥ 1 korzeń nie będzie w ogóle przestrzelony.

W niektórych przypadkach metodę Newtona można ustabilizować, stosując sukcesywną nadrelaksację , lub prędkość zbieżności można zwiększyć, stosując tę ​​samą metodę.

Nieruchomy punkt

W przypadku napotkania punktu stacjonarnego funkcji pochodna wynosi zero i metoda zakończy się z powodu dzielenia przez zero .

Słabe wstępne oszacowanie

Duży błąd wstępnego oszacowania może przyczynić się do braku zbieżności algorytmu. Aby przezwyciężyć ten problem, często można zlinearyzować optymalizowaną funkcję za pomocą rachunku różniczkowego, logarytmicznego, a nawet algorytmów ewolucyjnych, takich jak tunelowanie stochastyczne . Dobre wstępne szacunki są bliskie ostatecznemu globalnie optymalnemu oszacowaniu parametru. W regresji nieliniowej suma błędów kwadratów (SSE) jest tylko "blisko" paraboliczna w obszarze ostatecznych oszacowań parametrów. Znalezione tutaj wstępne szacunki pozwolą na szybkie osiągnięcie zbieżności metody Newtona-Raphsona. Tylko tutaj macierz Hesja SSE jest dodatnia, a pierwsza pochodna SSE jest bliska zeru.

Łagodzenie braku zbieżności

W solidnej implementacji metody Newtona powszechne jest nakładanie ograniczeń na liczbę iteracji, wiązanie rozwiązania z przedziałem, o którym wiadomo, że zawiera pierwiastek i łączenie metody z bardziej niezawodną metodą znajdowania pierwiastka.

Powolna zbieżność dla pierwiastków o krotności większej niż 1

Jeśli poszukiwany pierwiastek ma krotność większą niż jeden, współczynnik zbieżności jest jedynie liniowy (błędy pomniejszane o stały współczynnik na każdym kroku), chyba że zostaną podjęte specjalne kroki. Gdy istnieją dwa lub więcej pierwiastków, które są blisko siebie, może upłynąć wiele iteracji, zanim iteracje zbliżą się wystarczająco do jednego z nich, aby zbieżność kwadratowa była widoczna. Jeśli jednak znana jest krotność pierwiastka, poniższy zmodyfikowany algorytm zachowuje współczynnik zbieżności kwadratowej: ${\ Displaystyle m}$

${\ Displaystyle x_ {n + 1} = x_ {n}-m {\ Frac {f (x_ {n})} {f”(x_ {n})}}.}$

Jest to równoznaczne z używaniem kolejnej nadmiernej relaksacji . Z drugiej strony, jeśli krotność m pierwiastka nie jest znana, możliwe jest oszacowanie po wykonaniu jednej lub dwóch iteracji, a następnie wykorzystanie tej wartości do zwiększenia szybkości zbieżności. ${\ Displaystyle m}$

Jeśli krotność m pierwiastka jest skończona, to g ( x ) = f ( x ) / f ′ ( x ) będzie miał pierwiastek w tym samym miejscu co krotność 1. Zastosowanie metody Newtona do znalezienia pierwiastka g ( x ) wyzdrowieje zbieżność kwadratowa w wielu przypadkach, chociaż zazwyczaj obejmuje drugą pochodną f ( x ) . W szczególnie prostym przypadku, jeśli f ( x ) = x ^m to g ( x ) = x / m i metoda Newtona znajduje pierwiastek w pojedynczej iteracji z

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {g (x_ {n})} {g '(x_ {n})}} = x_ {n} - {\ Frac {x_ { n}/m}{1/m}}=0\,.}$

Analiza

Załóżmy, że funkcja F ma wartość zero na alfa , to jest f  ( a ) = 0 , a F jest różniczkowalną w sąsiedztwie z alfa .

Jeśli f jest różniczkowalną ciągły i jej pochodna jest niezerowe na  alfa , to istnieje sąsiedztwo z α , że dla wszystkich wartości wyjściowych X ₀ w tym sąsiedztwa, sekwencja ( x _n ) będzie zbiegają się alfa .

Jeżeli funkcja jest ciągle różniczkowalna, a jej pochodna nie jest równa 0 w α i ma drugą pochodną w α, to zbieżność jest kwadratowa lub szybsza. Jeśli druga pochodna nie jest równa 0 przy α, to zbieżność jest tylko kwadratowa. Jeżeli trzecia pochodna istnieje i jest ograniczona w sąsiedztwie α , to:

${\ Displaystyle \ Delta x_ {i + 1} = {\ Frac {f ''(\ alfa)} {2f '(\ alfa)}} (\ Delta x_ {i}) ^ {2} + O (\ Delta x_{i})^{3}\,,}$

gdzie

${\ Displaystyle \ Delta x_ {i} \ triangleq x_ {i} - \ alfa \,.}$

Jeśli pochodna wynosi 0 w α , to zbieżność jest zwykle tylko liniowa. W szczególności, jeśli f jest dwukrotnie w sposób ciągły różniczkowalny, f ′ ( α ) = 0 i f ″ ( α ) ≠ 0 , to istnieje sąsiedztwo α takie, że dla wszystkich wartości początkowych x ₀ w tym sąsiedztwie ciąg iteracji jest zbieżny liniowo, z szybkością 1/2 Alternatywnie, jeśli f ′ ( α ) = 0 i f ′ ( x ) ≠ 0 dla x ≠ α , x  w sąsiedztwie U z α , α jest zerem wielokrotności r , i jeśli f ∈ C ^r ( U ) , to istnieje takie sąsiedztwo α , że dla wszystkich wartości początkowych x ₀ w tym sąsiedztwie ciąg iteracji jest zbieżny liniowo.

Jednak nawet liniowa zbieżność nie jest gwarantowana w sytuacjach patologicznych.

W praktyce wyniki te mają charakter lokalny, a sąsiedztwo zbieżności nie jest z góry znane. Ale są też niektóre wyniki na globalnej konwergencji: na przykład, uzyskać prawo otoczenie U ₊ z alfa , jeśli f jest dwukrotnie różniczkowalna w U ₊ i jeśli f ' ≠ 0 , f · f " > 0 w U ₊ , a następnie, za każdy x ₀ w U ₊ ciąg x _k jest monotonicznie malejący do α .

Dowód zbieżności kwadratowej dla metody iteracyjnej Newtona

Zgodnie z twierdzeniem Taylora , każda funkcja f  ( x ), która ma ciągłą drugą pochodną, ​​może być reprezentowana przez rozwinięcie względem punktu, który jest bliski pierwiastkowi z f  ( x ) . Załóżmy, że ten pierwiastek to α . Wtedy rozwinięcie f  ( α ) o x _n wynosi:

${\ Displaystyle f (\ alfa) = f (x_ {n}) + f '(x_ {n}) (\ alfa -x_ {n}) + R_ {1} \,}$

( 1 )

gdzie forma Lagrange'a reszty z rozwinięcia szeregu Taylora jest

${\ Displaystyle R_ {1} = {\ Frac {1} {2!}} F'' (\ X _ {n}) (\ alfa -x_ {n}) ^ {2} \ ,,}$

gdzie ξ _n jest pomiędzy x _n i α .

Ponieważ α jest pierwiastkiem, ( 1 ) staje się:

${\ Displaystyle 0 = f (\ alfa) = f (x_ {n}) + f '(x_ {n}) (\ alfa -x_ {n}) + {\ tfrac {1} {2}} f '' (\xi _{n})(\alpha -x_{n})^{2}\,}$

( 2 )

Dzielenie równania ( 2 ) przez f ′ ( x _n ) i przestawianie daje

${\ Displaystyle {\ Frac {f (x_ {n})} {f '(x_ {n})}} + \ lewo (\ alfa -x_ {n} \ prawej) = {\ Frac {-f ''( \xi _{n})}{2f'(x_{n})}}\left(\alpha -x_{n}\right)^{2}}$

( 3 )

Pamiętając, że x _{n + 1} jest zdefiniowane przez

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f '(x_ {n})}} \ ,,}$

( 4 )

okazuje się, że

${\ Displaystyle \ underbrace {\ alfa -x_ {n + 1}} _ {\ varepsilon _ {n + 1}} = {\ Frac {-f ''(\ X _ {n})} {2f” (x_ {n})}}(\,\underbrace {\alpha -x_{n}} _{\varepsilon _{n}}\,)^{2}\,.}$

To jest,

${\ Displaystyle \ varepsilon _ {n + 1} = {\ Frac {-f ''(\ xi _ {n})} {2f '(x_ {n})}} \ cdot {\ varepsilon _ {n}} ^{2}\,.}$

( 5 )

Biorąc bezwzględną wartość obu stron daje

${\ Displaystyle \ lewo | {\ varepsilon _ {n + 1}} \ po prawej | = {\ Frac {\ po lewej | f '' (\ X _ {n}) \ po prawej | {2 \ po lewej | f '( x_{n})\right|}}\cdot {\varepsilon _{n}}^{2}\,.}$

( 6 )

Równanie ( 6 ) pokazuje, że szybkość zbieżności jest co najmniej kwadratowa, jeżeli spełnione są następujące warunki:

1. f ( x ) ≠ 0 ; dla wszystkich x ∈ I , gdzie I jest przedziałem [ α − r , α + r ] dla pewnego r ≥ | α − x ₀ | ;
2. f ″ ( x ) jest ciągła, dla wszystkich x ∈ I ;
3. x ₀ jest wystarczająco blisko pierwiastka α .

Termin wystarczająco bliski w tym kontekście oznacza:

Wreszcie ( 6 ) można wyrazić w następujący sposób:

${\ Displaystyle \ lewo | {\ varepsilon _ {n + 1}} \ prawo | \ leq M {\ varepsilon _ {n}} ^ {2} \,}$

gdzie M jest najwyższym współczynnikiem zmiennej ε _n ² na przedziale I określonym w warunku 1, czyli:

${\ Displaystyle M = \ sup _ {x \ w ja} {\ Frac {1} {2}} \ lewo | {\ Frac {f ''(x)} {f '(x)}} \ prawej |. \,}$

Punkt początkowy x ₀ należy wybrać tak, aby spełnione były warunki od 1 do 3, gdzie trzeci warunek wymaga, aby M | ε ₀ | < 1 .

Baseny atrakcji

Rozłączne podzbiory basenów przyciągania — obszary osi liczb rzeczywistych takie, że w każdym obszarze iteracja z dowolnego punktu prowadzi do jednego konkretnego pierwiastka — mogą być nieskończone i arbitralnie małe. Na przykład dla funkcji f  ( x ) = x ³ − 2 x ² − 11 x + 12 = ( x − 4)( x − 1)( x + 3) , w kolejnych basenach przyciągania występują następujące warunki początkowe:

2,352 875 27	zbiega się do	4;
2,352 841 72	zbiega się do	-3;
2,352 837 35	zbiega się do	4;
2,352 836 327	zbiega się do	-3;
2,352 836 323	zbiega się do	1.

Analiza awarii

Metoda Newtona gwarantuje zbieżność tylko wtedy, gdy spełnione są pewne warunki. Jeżeli założenia przyjęte w dowodzie zbieżności kwadratowej są spełnione, metoda będzie zbieżna. W kolejnych podrozdziałach brak zbieżności metody wskazuje, że założenia przyjęte w dowodzie nie zostały spełnione.

Złe punkty startowe

W niektórych przypadkach warunki na funkcji konieczne dla zbieżności są spełnione, ale punkt wybrany jako punkt początkowy nie znajduje się w przedziale, w którym metoda jest zbieżna. Może się to zdarzyć, na przykład, jeśli funkcja, której pierwiastek jest poszukiwany, zbliża się asymptotycznie do zera, gdy x idzie do ∞ lub −∞ . W takich przypadkach należy zastosować inną metodę, taką jak bisekcji , aby uzyskać lepsze oszacowanie zera, które będzie używane jako punkt początkowy.

Punkt iteracji jest nieruchomy

Rozważ funkcję:

${\ Displaystyle f (x) = 1-x ^ {2}.}$

Ma maksimum przy x = 0 i rozwiązania f  ( x ) = 0 przy x = ±1 . Jeśli zaczniemy iterację od punktu stacjonarnego x ₀ = 0 (gdzie pochodna wynosi zero), x ₁ będzie niezdefiniowane, ponieważ styczna w (0,1) jest równoległa do osi x :

${\ Displaystyle x_ {1}= x_ {0}-{\ Frac {f (x_ {0})} {f '(x_ {0})}} = 0-{\ Frac {1}{0}}. }$

Ten sam problem występuje, jeśli zamiast punktu początkowego dowolny punkt iteracji jest nieruchomy. Nawet jeśli pochodna jest mała, ale nie zerowa, następna iteracja będzie znacznie gorszym przybliżeniem.

Punkt początkowy wchodzi w cykl

Linie styczne x ³ − 2 x + 2 w punktach 0 i 1 przecinają oś x odpowiednio w punktach 1 i 0, ilustrując, dlaczego metoda Newtona oscyluje między tymi wartościami dla niektórych punktów początkowych.

W przypadku niektórych funkcji niektóre punkty początkowe mogą wejść w cykl nieskończony, zapobiegając zbieżności. Pozwolić

${\ Displaystyle f (x) = x ^ {3} -2 x + 2 \!}$

i weź 0 jako punkt początkowy. Pierwsza iteracja daje 1, a druga iteracja powraca do 0, więc sekwencja będzie zmieniać się między nimi bez zbieżności do pierwiastka. W rzeczywistości ten 2-cykl jest stabilny: istnieją sąsiedztwa wokół 0 i wokół 1, od których wszystkie punkty iterują asymptotycznie do 2-cyklu (a zatem nie do pierwiastka funkcji). Ogólnie zachowanie sekwencji może być bardzo złożone (zobacz fraktal Newtona ). Rzeczywiste rozwiązanie tego równania to−1.769 292 35 ….

Zagadnienia pochodne

Jeśli funkcja nie jest ciągle różniczkowalna w sąsiedztwie pierwiastka, to jest możliwe, że metoda Newtona zawsze będzie rozbieżna i zawiedzie, chyba że rozwiązanie zostanie odgadnięte za pierwszym razem.

Pochodna nie istnieje u źródła

Prostym przykładem funkcji, w której metoda Newtona jest rozbieżna, jest próba znalezienia pierwiastka sześciennego z zera. Pierwiastek sześcienny jest ciągły i nieskończenie różniczkowalny, z wyjątkiem x = 0 , gdzie jego pochodna jest nieokreślona:

${\ Displaystyle f (x) = {\ sqrt [{3}] {x}}.}$

Dla dowolnego punktu iteracji x _n następnym punktem iteracji będzie:

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f '(x_ {n})}} = x_ {n} - {\ Frac {{x_ {n}}^{\frac {1}{3}}}{{\frac {1}{3}}{x_{n}}^{{\frac {1}{3}}-1}}} =x_{n}-3x_{n}=-2x_{n}.}$

Algorytm przeskakuje rozwiązanie i ląduje po drugiej stronie osi y , dalej niż początkowo; zastosowanie metody Newtona faktycznie podwaja odległości od rozwiązania w każdej iteracji.

W rzeczywistości iteracje rozchodzą się do nieskończoności dla każdego f  ( x ) = | x | ^α , gdzie 0 < α <1/2. W granicznym przypadku α =1/2(pierwiastek kwadratowy), iteracje będą się zmieniać w nieskończoność między punktami x ₀ i − x ₀ , więc również w tym przypadku nie są zbieżne.

Pochodna nieciągła

Jeśli pochodna nie jest ciągła u pierwiastka, to zbieżność może nie wystąpić w dowolnym sąsiedztwie pierwiastka. Rozważ funkcję

${\ Displaystyle f (x) = {\ zacząć {przypadki} 0 i {\ tekst {jeśli}} x = 0 \ \ x + x ^ {2} \ grzech {\ Frac {2} {x}} i {\ tekst{if }}x\neq 0.\end{cases}}}$

Jego pochodną jest:

${\ Displaystyle f '(x) = {\ zacząć {przypadki} 1 i {\ tekst {jeśli}} x = 0 \ \ 1 + 2 x \ grzech {\ Frac {2} {x}} -2 \ cos {\ frac {2}{x}}&{\text{if }}x\neq 0.\end{cases}}}$

W dowolnym sąsiedztwie pierwiastka ta pochodna zmienia znak, gdy x zbliża się do 0 od prawej (lub od lewej), podczas gdy f  ( x ) ≥ x − x ² > 0 dla 0 < x < 1 .

Więc f  ( x )/f ( x ) jest nieograniczona w pobliżu korzenia, a metoda Newtona będzie rozbieżna prawie wszędzie w każdym sąsiedztwie, nawet jeśli:

• funkcja jest wszędzie różniczkowalna (a więc ciągła);
• pochodna na pierwiastku jest niezerowa;
• f jest nieskończenie różniczkowalna z wyjątkiem pierwiastka; oraz
• pochodna jest ograniczona w sąsiedztwie pierwiastka (w przeciwieństwie do f  ( x )/f ( x )).

Zbieżność niekwadratowa

W niektórych przypadkach iteracje zbiegają się, ale nie są zbieżne tak szybko, jak obiecano. W tych przypadkach prostsze metody zbiegają się tak szybko, jak metoda Newtona.

Zero pochodna

Jeśli pierwsza pochodna ma pierwiastek równy zero, to zbieżność nie będzie kwadratowa. Pozwolić

${\ Displaystyle f (x) = x ^ {2} \!}$

wtedy f ′ ( x ) = 2 x i w konsekwencji

${\ Displaystyle x-{\ Frac {f (x)} {f '(x)}} = {\ Frac {x} {2}}.}$

Zatem zbieżność nie jest kwadratowa, chociaż funkcja jest wszędzie nieskończenie różniczkowalna.

Podobne problemy pojawiają się nawet wtedy, gdy korzeń jest tylko „prawie” podwójny. Na przykład niech

${\ Displaystyle f (x) = x ^ {2} (x-1000) + 1.}$

Wtedy pierwsze kilka iteracji zaczynających się od x ₀ = 1 to

x ₀ = 1

x ₁ =0,500 250 376 …

x ₂ =0,251 062 828 …

x ₃ =0,127 507 934 …

x ₄ =0,067 671 976 …

x ₅ =0,041 224 176 …

x ₆ =0,032 741 218 …

x ₇ =0,031 642 362 …

potrzeba sześciu iteracji, aby osiągnąć punkt, w którym zbieżność wydaje się być kwadratowa.

Brak drugiej pochodnej

Jeśli nie ma drugiej pochodnej przy pierwiastku, zbieżność może nie być kwadratowa. Pozwolić

${\ Displaystyle f (x) = x + x ^ {\ Frac {4}{3}}.}$

Następnie

${\ Displaystyle f '(x) = 1 + {\ tfrac {4}{3}} x ^ {\ Frac {1} {3}}.}$

I

${\ Displaystyle f ''(x) = {\ tfrac {4} {9}} x ^ {- {\ Frac {2} {3}}}}$

z wyjątkiem sytuacji, gdy x = 0, gdzie jest niezdefiniowane. Biorąc pod uwagę x _n ,

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f '(x_ {n})}} = {\ Frac {{\ Frac {1} { 3}}{x_{n}}^{\frac {4}{3}}}{1+{\tfrac {4}{3}}{x_{n}}^{\frac {1}{3} }}}}$

który ma około 4/3razy tyle bitów precyzji, ile ma x _n . To mniej niż 2 razy więcej, niż byłoby to wymagane dla zbieżności kwadratowej. Zatem zbieżność metody Newtona (w tym przypadku) nie jest kwadratowa, chociaż: funkcja jest wszędzie ciągle różniczkowalna; pochodna nie jest zerem u pierwiastka; i f jest nieskończenie różniczkowalna z wyjątkiem pożądanego pierwiastka.

Uogólnienia

Złożone funkcje

Baseny przyciągania dla x ⁵ − 1 = 0 ; ciemniejszy oznacza więcej iteracji do zbieżności.

Kiedy mamy do czynienia z funkcjami złożonymi , metoda Newtona może być bezpośrednio zastosowana do znalezienia ich zer. Każde zero ma basen przyciągania na płaszczyźnie zespolonej, zbiór wszystkich wartości początkowych, które powodują zbieżność metody do tego konkretnego zera. Zestawy te można odwzorować jak na pokazanym obrazku. Dla wielu złożonych funkcji granice basenów przyciągania są fraktalami .

W niektórych przypadkach istnieją regiony na płaszczyźnie zespolonej, które nie znajdują się w żadnym z tych basenów przyciągania, co oznacza, że ​​iteracje nie są zbieżne. Na przykład, jeśli użyjemy rzeczywistego warunku początkowego do znalezienia pierwiastka x ² + 1 , wszystkie kolejne iteracje będą liczbami rzeczywistymi, a zatem iteracje nie mogą zbiegać się do żadnego z pierwiastków, ponieważ oba pierwiastki są nierzeczywiste. W tym przypadku prawie wszystkie rzeczywiste warunki początkowe prowadzą do zachowania chaotycznego , podczas gdy niektóre warunki początkowe iterują albo do nieskończoności, albo do powtarzających się cykli o dowolnej skończonej długości.

Curt McMullen wykazał, że dla dowolnego możliwego algorytmu czysto iteracyjnego podobnego do metody Newtona, algorytm będzie rozbieżny w niektórych otwartych obszarach płaszczyzny zespolonej, gdy zostanie zastosowany do pewnego wielomianu stopnia 4 lub wyższego. Jednak McMullen podał ogólnie zbieżny algorytm dla wielomianów stopnia 3.

Metoda trzeciego rzędu Czebyszewa

iteracja Nasha-Mosera

Układy równań

k zmiennych, k funkcji

Można również zastosować metodę Newtona do rozwiązywania układów równań, co sprowadza się do znajdowania (jednoczesnych) zer funkcji ciągle różniczkowalnych . Jest to równoważne znalezieniu zer pojedynczej funkcji o wartościach wektorowych . W powyższym sformułowaniu skalary są zastąpione wektorami i zamiast dzielenia funkcji przez jej pochodną należy pozostawić pomnożenie funkcji przez odwrotność jej macierzy jakobianu . Powoduje to wyrażenie ${\displaystyle k}$${\displaystyle k}$${\ Displaystyle f: \ mathbb {R} \ do \ mathbb {R}}$${\ Displaystyle F: \ mathbb {R} ^ {k} \ do \ mathbb {R} ^ {k}}$${\displaystyle x_{n}}$${\ Displaystyle \ mathbf {x} _ {n}}$${\ Displaystyle f (x_ {n})}$${\ Displaystyle f '(x_ {n})}$${\ Displaystyle F (\ mathbf {x} _ {n})}$${\displaystyle k\razy k}$ ${\ Displaystyle J_ {F} (\ mathbf {x} _ {n})}$

${\ Displaystyle \ mathbf {x} _ {n + 1} = \ mathbf {x} _ {n}-J_ {F} (\ mathbf {x} _ {n}) ^ {-1} F (\ mathbf { x} _{n})}$.

Zamiast faktycznie obliczać odwrotność macierzy Jakobianu, można zaoszczędzić czas i zwiększyć stabilność numeryczną, rozwiązując układ równań liniowych

${\ Displaystyle J_ {F} (\ mathbf {x} _ {n}) (\ mathbf {x} _ {n + 1} - \ mathbf {x} _ {n}) = - F (\ mathbf {x} _{n})}$

dla nieznanego . ${\ Displaystyle \ mathbf {x} _ {n + 1} - \ mathbf {x} _ {n}}$

k zmiennych, m równań, gdzie m > k

K wymiarową wariant metoda Newtona mogą być wykorzystywane w celu rozwiązania układów większy niż K (nieliniowych) równania oraz jeśli algorytm wykorzystuje uogólnioną odwrotność z niekwadratowych jakobian matrycy J ⁺ = ( J ^t J ) ^-1 J ^T zamiast odwrotności J. Jeśli układ nieliniowy nie ma rozwiązania, metoda próbuje znaleźć rozwiązanie w nieliniowym sensie najmniejszych kwadratów . Zobacz algorytm Gaussa-Newtona, aby uzyskać więcej informacji.

W przestrzeni Banacha

Innym uogólnieniem jest metoda Newtona znajdowania pierwiastka funkcjonału F zdefiniowanego w przestrzeni Banacha . W tym przypadku sformułowanie to

${\ Displaystyle X_ {n + 1} = X_ {n} - {\ Bigl (} F '(X_ {n}) {\ Bigr)} ^ {-1} F (X_ {n}), \,}$

gdzie F ' ( x _n ) jest pochodną Fréchet obliczane przy X _n . Aby metoda mogła być zastosowana, pochodna Frécheta musi być w pełni odwracalna w każdym X _n . Warunkiem istnienia i zbieżności z pierwiastkiem jest twierdzenie Newtona-Kantorovicha .

Powyżej p numery -adic

W analizie p- adycznej standardową metodą pokazania równania wielomianowego w jednej zmiennej ma pierwiastek p- adyczny jest lemat Hensela , który wykorzystuje rekurencję z metody Newtona na liczbach p- adycznych. Ze względu na bardziej stabilne zachowanie dodawania i mnożenia w liczbach p -adycznych w porównaniu z liczbami rzeczywistymi (w szczególności kulka jednostkowa w p -adice jest pierścieniem), zbieżność w lemie Hensela można zagwarantować przy znacznie prostszych hipotezach niż w klasyczna metoda Newtona na linii rzeczywistej.

Metoda Newtona-Fouriera

Metoda Newtona-Fouriera jest rozszerzeniem metody Newtona Josepha Fouriera w celu zapewnienia granic błędu bezwzględnego aproksymacji pierwiastka, przy jednoczesnym zapewnieniu zbieżności kwadratowej.

Załóżmy, że f  ( x ) jest dwa razy w sposób ciągły różniczkowalny na [ a , b ] i że f zawiera pierwiastek w tym przedziale. Załóżmy, że f ′ ( x ), f ″ (x) ≠ 0 na tym przedziale (jest to na przykład przypadek, gdy f  ( a ) < 0 , f  ( b ) > 0 i f ′ ( x ) > 0 , oraz f ″ ( x ) > 0 w tym przedziale). Gwarantuje to, że na tym przedziale istnieje unikalny pierwiastek, nazwijmy go α . Jeśli jest wklęsły w dół zamiast wklęsły, zastąp f  ( x ) przez − f  ( x ), ponieważ mają te same pierwiastki.

Niech x ₀ = b będzie prawym punktem końcowym przedziału i niech z ₀ = a będzie lewym punktem końcowym przedziału. Biorąc pod uwagę x _n , zdefiniuj

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f”(x_ {n})}}}$

co jest po prostu metodą Newtona, jak poprzednio. Następnie zdefiniuj

${\ Displaystyle z_ {n + 1} = z_ {n} - {\ Frac {f (z_ {n})} {f '(x_ {n})}}}$

gdzie mianownikiem jest f ( x _n ) a nie f ′ ( z _n ) . Iteracje x _n będą ściśle maleć do pierwiastka, podczas gdy iteracje z _n będą ściśle rosnąć do pierwiastka. Także,

${\ Displaystyle \ lim _ {n \ do \ infty} {\ Frac {x_ {n + 1}-z_ {n + 1}} {(x_ {n}-z_ {n}) ^ {2}}} = {\frac {f''(\alfa )}{2f'(\alfa )}}}$

tak, że odległość między x _n i z _n zmniejsza się kwadratowo.

Metody quasi-Newtona

Gdy jakobian jest niedostępny lub zbyt kosztowny do obliczenia w każdej iteracji, można zastosować metodę quasi-Newtona .

q-analogowy

Metodę Newtona można uogólnić za pomocą q-analogu zwykłej pochodnej.

Zmodyfikowane metody Newtona

Procedura Maehly'ego

Równanie nieliniowe ma ogólnie wiele rozwiązań. Ale jeśli wartość początkowa nie jest odpowiednia, metoda Newtona może nie być zbieżna do pożądanego rozwiązania lub może być zbieżna do tego samego rozwiązania znalezionego wcześniej. Gdy już znaleźliśmy N rozwiązań , to następny pierwiastek można znaleźć, stosując metodę Newtona do następnego równania: ${\ Displaystyle f (x) = 0}$

${\ Displaystyle F (x) = {\ Frac {f (x)} {\ prod _ {i = 1} ^ {N} (x-x_ {i})}} = 0.}$

Metoda ta jest stosowana do uzyskania zer funkcji Bessela drugiego rodzaju.

Zmodyfikowana metoda Newtona Hirano

Zmodyfikowana metoda Newtona Hirano jest modyfikacją zachowującą zbieżność metody Newtona i unikającą niestabilności. Został opracowany do rozwiązywania złożonych wielomianów.

Metoda interwałowa Newtona

Połączenie metody Newtona z arytmetyką przedziałową jest bardzo przydatne w niektórych kontekstach. Daje to kryterium zatrzymania, które jest bardziej wiarygodne niż zwykłe (które są małą wartością funkcji lub małą zmianą zmiennej między kolejnymi iteracjami). Może to również wykryć przypadki, w których metoda Newtona jest zbieżna teoretycznie, ale rozbieżna numerycznie z powodu niewystarczającej precyzji zmiennoprzecinkowej (jest to zwykle przypadek wielomianów o dużym stopniu, gdzie bardzo mała zmiana zmiennej może dramatycznie zmienić wartość funkcji ; patrz wielomian Wilkinsona ).

Zastanów się , gdzie jest prawdziwa przerwa, i załóżmy, że mamy przedział rozszerzenia z , co oznacza, że przyjmuje na wejściu interwał i wyprowadza przerwa taka, że: ${\ Displaystyle f \ w {\ mathcal {C}} ^ {1} (X)}$${\ Displaystyle X}$${\displaystyle F'}$${\displaystyle f'}$${\displaystyle F'}$${\displaystyle Y\subseteq X}$${\ Displaystyle F'(Y)}$

${\ Displaystyle {\ zacząć {wyrównany} F '([y, y]) i = \ {f' (y) \} \ \ [5pt] F '(Y) i \ supseteq \ {f' (y) \ w połowie y\w Y\}.\end{wyrównany}}}$

Zakładamy również, że , a więc w szczególności ma co najwyżej jeden korzeń w . Następnie definiujemy interwałowy operator Newtona przez: ${\displaystyle 0\notin F'(X)}$${\displaystyle f}$${\ Displaystyle X}$

${\ Displaystyle N (Y) = m-{\ Frac {f (m)} {f '(Y)}} = \ lewo \ {\ lewo. m {\ Frac {f (m)} {z}} ~\prawo|~z\in F'(Y)\prawo\}}$

gdzie . Zwróć uwagę, że hipoteza na implikuje, że jest dobrze zdefiniowana i jest przedziałem (zobacz arytmetykę przedziałową, aby uzyskać więcej informacji na temat operacji przedziałowych). To naturalnie prowadzi do następującej sekwencji: ${\displaystyle m\w Y}$${\displaystyle F'}$${\ Displaystyle N (Y)}$

${\ Displaystyle {\ zacząć {wyrównany} X_ {0}& = X \ \ X_ {k + 1} i = N (X_ {k}) \ czapka X_ {k}. \ koniec {wyrównany}}}$

W Twierdzenie Lagrange'a zapewnia, że jeśli nie jest pierwiastkiem w , to również w . Co więcej, hipoteza na zapewnia, że jest co najwyżej o połowę mniejsza od tego, co kiedy jest punktem środkowym , więc ta sekwencja zbiega się w kierunku , gdzie jest pierwiastkiem in . ${\displaystyle f}$${\ Displaystyle X_ {k}}$${\ Displaystyle X_ {k + 1}}$${\displaystyle F'}$${\ Displaystyle X_ {k + 1}}$${\ Displaystyle X_ {k}}$${\ Displaystyle m}$${\ Displaystyle Y}$${\ Displaystyle [x ^ {*}, x ^ {*}]}$${\ Displaystyle x ^ {*}}$${\displaystyle f}$${\ Displaystyle X}$

Jeśli ściśle zawiera , użycie rozszerzonego dzielenia interwałowego tworzy sumę dwóch interwałów dla  ; wiele pierwiastków jest zatem automatycznie oddzielanych i ograniczanych. ${\ Displaystyle F'(X)}$${\ Displaystyle 0}$${\ Displaystyle N (X)}$

Aplikacje

Problemy minimalizacji i maksymalizacji

Metoda Newtona może być użyta do znalezienia minimum lub maksimum funkcji . Pochodna wynosi zero w minimum lub maksimum, więc lokalne minima i maksima można znaleźć stosując metodę Newtona do pochodnej. Iteracja staje się: ${\displaystyle f(x)}$

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f '(x_ {n})} {f ''(x_ {n})}}.}$

Odwrotność multiplikatywna liczb i szeregów potęgowych

Ważnym zastosowaniem jest dzielenie Newtona-Raphsona , które można wykorzystać do szybkiego znalezienia odwrotności liczby a , używając tylko mnożenia i odejmowania, czyli liczby x takiej, że1/x= . Możemy to przeformułować jako znalezienie zera f ( x ) =1/x- . Mamy f ′( x ) = −1/x ².

Iteracja Newtona to

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f '(x_ {n})}} = x_ {n} + {\ Frac {{\ frac {1}{x_{n}}}-a}{\frac {1}{x_{n}^{2}}}}=x_{n}(2-ax_{n}).}$

Dlatego iteracja Newtona wymaga tylko dwóch mnożeń i jednego odejmowania.

Ta metoda jest również bardzo wydajna przy obliczaniu odwrotności multiplikatywnej szeregu potęgowego .

Rozwiązywanie równań transcendentalnych

Wiele równań transcendentalnych można rozwiązać metodą Newtona. Biorąc pod uwagę równanie

${\ Displaystyle g (x) = h (x)}$

gdzie g ( x ) i/lub h ( x ) jest funkcją transcendentalną , piszemy

${\displaystyle f(x)=g(x)-h(x).}$

Wartości x, które rozwiązują pierwotne równanie, są zatem pierwiastkami f  ( x ) , które można znaleźć metodą Newtona.

Uzyskiwanie zer funkcji specjalnych

Metodę Newtona stosuje się do ilorazu funkcji Bessela w celu uzyskania jego pierwiastka.

Weryfikacja numeryczna rozwiązań równań nieliniowych

Numeryczna weryfikacja rozwiązań równań nieliniowych została przeprowadzona przy wielokrotnym zastosowaniu metody Newtona i utworzeniu zbioru możliwych rozwiązań.

Modelowanie CFD

Zastosowano iteracyjną procedurę Newtona-Raphsona w celu narzucenia stabilnych warunków brzegowych Dirichleta w CFD , jako dość ogólną strategię modelowania rozkładu prądu i potencjału dla stosów ogniw elektrochemicznych.

Przykłady

Pierwiastek kwadratowy

Rozważ problem znalezienia pierwiastka kwadratowego z liczby a , to znaczy liczby dodatniej x takiej, że x ² = a . Metoda Newtona jest jedną z wielu metod obliczania pierwiastków kwadratowych . Możemy to przeformułować jako znalezienie zera f ( x ) = x ² − a . Mamy f ( x ) = 2 x .

Na przykład, aby znaleźć pierwiastek kwadratowy z 612 z początkowym przypuszczeniem x ₀ = 10 , ciąg podany metodą Newtona to:

${\ Displaystyle {\ zacząć {macierz} x_ {1}& = & x_ {0}-{\ dfrac {f (x_ {0})} {f '(x_ {0})}} & = i 10- {\ dfrac {10^{2}-612}{2\times 10}}&=&35.6\qquad \qquad \qquad \quad \;\,{}\\x_{2}&=&x_{1}-{\ dfrac {f(x_{1})}{f'(x_{1})}}&=&35.6-{\dfrac {35.6^{2}-612}{2\times 35.6}}&=&{ \underline {2}}6.395\,505\,617\,978\kropki \\x_{3}&=&\vkropki &=&\vkropki &=&{\underline {24.7}}90\,635\, 492\,455\kropki \\x_{4}&=&\vkropki &=&\vkropki &=&{\underline {24.738\,6}}88\,294\,075\kropki \\x_{5} &=&\vkropki &=&\vkropki &=&{\podkreślenie {24.738\,633\,753\,7}}67\kropek \end{matryca}}}$

gdzie prawidłowe cyfry są podkreślone. Wystarczy kilka iteracji, aby uzyskać rozwiązanie z dokładnością do wielu miejsc po przecinku.

Przekształcenie wzoru w następujący sposób daje babilońską metodę znajdowania pierwiastków kwadratowych :

${\ Displaystyle x_ {n + 1} = x_ {n} - {\ Frac {f (x_ {n})} {f '(x_ {n})}} = x_ {n} - {\ Frac {x_ { n}^{2}-a}{2x_{n}}}={\frac {1}{2}}{\biggl (}2x_{n}-{\Bigl (}x_{n}-{\frac {a}{x_{n}}}{\Bigr )}{\biggr )}={\frac {1}{2}}{\Bigl (}x_{n}+{\frac {a}{x_{ n}}}{\Większy )}}$

tj. średnia arytmetyczna domysłu, x _n ia/x _n.

Rozwiązanie cos( x ) = x ³

Rozważ problem znalezienia liczby dodatniej x przy cos( x ) = x ³ . Możemy to przeformułować jako znalezienie zera f ( x ) = cos( x ) − x ³ . Mamy f ′( x ) = −sin( x ) − 3 x ² . Ponieważ cos( x ) ≤ 1 dla wszystkich x i x ³ > 1 dla x > 1 , wiemy, że nasze rozwiązanie leży między 0 a 1.

Na przykład, przy początkowym zgadywaniu x ₀ = 0,5 , sekwencja podana metodą Newtona to (zauważ, że wartość początkowa równa 0 doprowadzi do niezdefiniowanego wyniku, pokazującego znaczenie użycia punktu początkowego, który jest bliski rozwiązania):

${\ Displaystyle {\ zacząć {macierz} x_ {1} i = i x_ {0}-{\ dfrac {f (x_ {0})} {f '(x_ {0})}} i = i 0,5- { \dfrac {\cos 0.5-0.5^{3}}{-\sin 0.5-3\razy 0.5^{2}}}&=&1.112\,141\,637\,097\kropki \\x_{2 }&=&x_{1}-{\dfrac {f(x_{1})}{f'(x_{1})}}&=&\vdots &=&{\underline {0.}}909\, 672\,693\,736\kropki \\x_{3}&=&\vkropki &=&\vkropki &=&{\underline {0.86}}7\,263\,818\,209\kropki \\x_ {4}&=&\vkropki &=&\vkropki &=&{\podkreśl {0.865\,47}}7\,135\,298\kropki \\x_{5}&=&\vkropki &=&\ vkropki &=&{\underline {0.865\,474\,033\,1}}11\kropki \\x_{6}&=&\vkropki &=&\vkropki &=&{\underline {0.865\,474 \,033\,102}}\kropki \end{matryca}}}$

W powyższym przykładzie prawidłowe cyfry są podkreślone. W szczególności x ₆ jest poprawne do 12 miejsc po przecinku. Widzimy, że liczba poprawnych cyfr po przecinku wzrasta z 2 (dla x ₃ ) do 5 i 10, ilustrując zbieżność kwadratową.

Kod

Poniżej znajduje się przykład implementacji metody Newtona w języku programowania Julia do znajdowania pierwiastka funkcji, fktóra ma pochodną fprime.

Początkowe przypuszczenie to x ₀ = 1, a funkcja będzie miała postać f ( x ) = x ² − 2 tak, że f ′( x ) = 2 x .

Każda nowa iteracja metody Newtona będzie oznaczona przez x1. Podczas obliczeń sprawdzimy, czy mianownik ( yprime) staje się zbyt mały (mniejszy niż epsilon), co miałoby miejsce, gdyby f ′( x _n ) ≈ 0 , ponieważ w przeciwnym razie można by wprowadzić duży błąd.

x0            = 1         # The initial guess
f(x)          = x^2 - 2   # The function whose root we are trying to find
fprime(x)     = 2x        # The derivative of the function
tolerance     = 1e-7      # 7 digit accuracy is desired
epsilon       = 1e-14     # Do not divide by a number smaller than this
maxIterations = 20        # Do not allow the iterations to continue indefinitely
solutionFound = false     # Have not converged to a solution yet

for i = 1:maxIterations
  y      = f(x0)
  yprime = fprime(x0)

  if abs(yprime) < epsilon            # Stop if the denominator is too small
    break
  end

  global x1 = x0 - y/yprime           # Do Newton's computation

  if abs(x1 - x0) <= tolerance        # Stop when the result is within the desired tolerance
    global solutionFound = true
    break
  end

  global x0 = x1                      # Update x0 to start the process again
end

if solutionFound
  println("Solution: ", x1)           # x1 is a solution within tolerance and maximum number of iterations
else
  println("Did not converge")         # Newton's method did not converge
end

Zobacz też

Uwagi

Bibliografia

• Gil, A.; Segura, J.; Temme, Nowy Meksyk (2007). Metody numeryczne dla funkcji specjalnych . Towarzystwo Matematyki Przemysłowej i Stosowanej. Numer ISBN 978-0-89871-634-4.
• Sulli, Endre ; Mayers, Dawid (2003). Wprowadzenie do analizy numerycznej . Wydawnictwo Uniwersytetu Cambridge. Numer ISBN 0-521-00794-1.

Dalsza lektura

• Kendall E. Atkinson, Wprowadzenie do analizy numerycznej , (1989) John Wiley & Sons, Inc, ISBN  0-471-62489-6
• Tjalling J. Ypma, Historyczny rozwój metody Newtona–Raphsona, SIAM Review 37 (4), 531–551, 1995. doi : 10.1137/1037125 .
• Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude ; Sagastizábal, Claudia A. (2006). Optymalizacja numeryczna: Aspekty teoretyczne i praktyczne . Universitext (drugie poprawione wydanie tłumaczenia z 1997 r. wyd. francuskie). Berlin: Springer-Verlag. s. XIV+490. doi : 10.1007/978-3-540-35447-5 . Numer ISBN 3-540-35445-X. MR  2265882 .
• P. Deuflhard, Metody Newtona dla problemów nieliniowych. Niezmienność afiniczna i algorytmy adaptacyjne. Seria Springera w matematyce obliczeniowej, tom. 35. Springer, Berlin, 2004. ISBN  3-540-21099-7 .
• CT Kelley, Rozwiązywanie równań nieliniowych metodą Newtona , nr 1 w Podstawach Algorytmów, SIAM, 2003. ISBN  0-89871-546-6 .
• JM Ortega, WC Rheinboldt, Iteracyjne rozwiązanie równań nieliniowych w kilku zmiennych. Klasyka w matematyce stosowanej, SIAM, 2000. ISBN  0-89871-461-3 .
• Prasa, WH; Teukolski SA; Vetterling, WT; Flannery, BP (2007). „Rozdział 9. Znajdowanie pierwiastków i nieliniowe zbiory równań próbkowania ważności” . Przepisy numeryczne: The Art of Scientific Computing (3rd ed.). Nowy Jork: Cambridge University Press. Numer ISBN 978-0-521-88068-8.. Zobacz zwłaszcza sekcje 9.4 , 9.6 i 9.7 .
• Avriel, Mordechaj (1976). Programowanie nieliniowe: analiza i metody . Sala Prezydencka. s. 216-221. Numer ISBN 0-13-623603-0.

Zewnętrzne linki

• „Metoda Newtona” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Weisstein, Eric W. „Metoda Newtona” . MatematykaŚwiat .
• Metoda Newtona, Citizendium.
• Mathews, J., Przyspieszone i zmodyfikowane metody Newtona, Notatki z kursu.
• Wu, X., Korzenie równań, Notatki do kursu.