Potrójny pitagorejski - Pythagorean triple
Pitagorasa potrójne składa się z trzech dodatnich liczb całkowitych a , b i c tak, że 2 + b 2 = C 2 . Taka trójka jest powszechnie pisana ( a , b , c ) , a dobrze znanym przykładem jest (3, 4, 5) . Jeśli ( a , b , c ) jest trójką pitagorejską, to ( ka , kb , kc ) jest również dla dowolnej dodatniej liczby całkowitejk . Prymitywny Pitagorasa potrójne jest w której, b i c są względnie pierwsze (to znaczy, że nie mają wspólny dzielnik większy niż 1). Trójkąt, którego boki tworzą trójkę pitagorejską, nazywa się trójkątem pitagorejskim i jest z konieczności trójkątem prostokątnym .
Nazwa wywodzi się z twierdzenia Pitagorasa , stwierdzającego, że każdy trójkąt prostokątny ma długość boków spełniającą wzór a 2 + b 2 = c 2 ; tak więc trójki pitagorejskie opisują trzy całkowite długości boków trójkąta prostokątnego. Jednak trójkąty prostokątne o bokach niecałkowitych nie tworzą trójek pitagorejskich. Na przykład trójkąt o bokach a = b = 1 i c = √ 2 jest trójkątem prostokątnym, ale (1, 1, √ 2 ) nie jest trójką pitagorejską, ponieważ √ 2 nie jest liczbą całkowitą. Co więcej, 1 i √ 2 nie mają całkowitej wspólnej wielokrotności, ponieważ √ 2 jest niewymierne .
Trójki pitagorejskie znane są od czasów starożytnych. Najstarszy znany zapis pochodzi z Plimpton 322 , babilońskiej glinianej tabliczki z około 1800 roku pne, zapisanej w systemie liczb sześćdziesiętnych . Został odkryty przez Edgara Jamesa Banksa wkrótce po 1900 roku i sprzedany George'owi Arthurowi Plimptonowi w 1922 roku za 10 dolarów.
Szukając rozwiązań liczb całkowitych, równanie a 2 + b 2 = c 2 jest równaniem diofantycznym . Tak więc trójki pitagorejskie należą do najstarszych znanych rozwiązań nieliniowego równania diofantycznego.
Przykłady
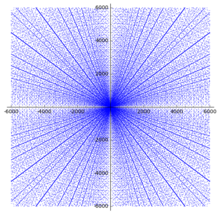
Istnieje 16 prymitywnych trójek pitagorejskich liczb do 100:
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Każdy z tych punktów tworzy promieniującą linię na wykresie punktowym. Inne małe trójki pitagorejskie, takie jak (6, 8, 10) nie są wymienione, ponieważ nie są prymitywne; na przykład (6, 8, 10) jest wielokrotnością (3, 4, 5).
Dodatkowo są to pozostałe prymitywne trójki pitagorejskie liczb do 300:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Generowanie trójki

Wzór euklidesowej jest podstawowym Wzór generowania pitagorejską trójek podane dowolną parę liczb m i n o m > n > 0 . Formuła mówi, że liczby całkowite
tworzą trójkę pitagorejską. Trójka generowana przez wzór Euklidesa jest pierwotna wtedy i tylko wtedy, gdy m i n są względnie pierwsze, a nie oba są nieparzyste. Gdy oba m i n są nieparzyste, wtedy a , b i c będą parzyste, a trójka nie będzie pierwotna; jednak dzielenie a , b i c przez 2 da prymitywną trójkę, gdy m i n są względnie pierwsze i oba są nieparzyste.
Każdy prymitywny powstaje potrójne (po wymianie i B , jeżeli nawet) z unikalną parę liczb względnie pierwsze m , n , z których jeden jest parzyste. Wynika z tego, że istnieje nieskończenie wiele prymitywnych trójek pitagorejskich. Ta zależność między a , b i c do m oraz n ze wzoru Euklidesa jest przywoływana w dalszej części tego artykułu.
Pomimo wygenerowania wszystkich prymitywnych trójek, wzór Euklidesa nie generuje wszystkich trójek — na przykład (9, 12, 15) nie można wygenerować za pomocą liczb całkowitych m i n . Można temu zaradzić, wstawiając do wzoru dodatkowy parametr k . Poniższe informacje wygenerują wszystkie trójki pitagorejskie w unikalny sposób:
gdzie m , n i k są dodatnimi liczbami całkowitymi z m > n , oraz z m i n względnie pierwszymi, a nie obiema nieparzystymi.
To, że te formuły generują trójki pitagorejskie, można zweryfikować, rozwijając a 2 + b 2 przy użyciu algebry elementarnej i sprawdzając, czy wynik jest równy c 2 . Ponieważ każdą trójkę pitagorejską można podzielić przez pewną liczbę całkowitą k, aby otrzymać pierwotną trójkę, każdą trójkę można wygenerować jednoznacznie, używając wzoru z m i n, aby wygenerować swój pierwotny odpowiednik, a następnie pomnożyć przez k, jak w ostatnim równaniu.
Wybranie m i n z pewnych ciągów całkowitych daje interesujące wyniki. Na przykład, jeśli m i n są kolejnymi liczbami Pella , a i b będą się różnić o 1.
Wiele formuł do generowania trójek o określonych właściwościach zostało opracowanych od czasów Euklidesa.
Dowód wzoru Euklidesa
To, że spełnienie wzoru Euklidesa przez a, b, c jest wystarczające, aby trójkąt był pitagorejski, wynika z faktu, że dla dodatnich liczb całkowitych m i n , m > n , a, b i c podane we wzorze są dodatnie liczb całkowitych oraz z faktu, że
Dowód na konieczność , że a, b, c, wyrażone wzorem Euklidesa jakiegokolwiek pierwotnego pitagorejsko potrójne jest w następujący sposób. Wszystkie takie prymitywne trójki można zapisać jako ( a , b , c ) , gdzie a 2 + b 2 = c 2 i a , b , c są względnie pierwsze . Zatem a , b , c są względnie pierwsze parami (gdyby liczba pierwsza podzieliła dwie z nich, musiałaby również podzielić trzecią). Ponieważ a i b są względnie pierwsze, co najmniej jeden z nich jest nieparzysty, więc możemy przypuszczać, że a jest nieparzyste, zamieniając w razie potrzeby a i b . Oznacza to, że b jest parzyste, a c nieparzyste (gdyby b było nieparzyste, c byłoby parzyste, a c 2 byłoby wielokrotnością 4, podczas gdy a 2 + b 2 byłoby przystające do 2 modulo 4, ponieważ nieparzysty kwadrat jest zgodny z 1 modułem 4).
Od otrzymujemy i stąd . Następnie . Ponieważ jest racjonalne, ustawiamy go na najniższym poziomie. Tak więc , będąc wzajemnością . Następnie rozwiązywanie
za i daje
Ponieważ jest całkowicie zredukowane, m i n są względnie pierwsze i nie mogą być obydwa parzyste. Gdyby oba były nieparzyste, licznik byłby wielokrotnością 4 (ponieważ nieparzysty kwadrat jest przystający do 1 modulo 4), a mianownik 2 mn nie byłby wielokrotnością 4. Ponieważ 4 byłoby najmniejszym możliwym parzystym współczynnikiem w liczniku i 2 byłoby maksymalnym możliwym współczynnikiem parzystym w mianowniku, co sugerowałoby, że a jest parzyste, pomimo zdefiniowania go jako nieparzystego. Zatem jeden z m i n jest nieparzysty, a drugi parzysty, a liczniki dwóch ułamków z mianownikiem 2 mn są nieparzyste. Zatem te ułamki są w pełni zredukowane (nieparzysta liczba pierwsza dzieląca ten mianownik dzieli jeden z m i n, ale nie drugi; zatem nie dzieli m 2 ± n 2 ). Można więc zrównać liczniki z licznikami i mianowniki z mianownikami, dając wzór Euklidesa
- z m i n względnie pierwszymi i o przeciwnych parytetach.
Dłuższy, ale bardziej powszechny dowód podają Maor (2007) i Sierpiński (2003). Inny dowód jest podany w równaniu diofantycznym § Przykład trójek pitagorejskich , jako przykład ogólnej metody, która ma zastosowanie do każdego jednorodnego równania diofantycznego drugiego stopnia.
Interpretacja parametrów we wzorze Euklidesa
Załóżmy, że boki trójkąta pitagorejskiego mają długości m 2 − n 2 , 2 mn i m 2 + n 2 , i załóżmy, że kąt między ramieniem o długości m 2 − n 2 a przeciwprostokątną o długości m 2 + n 2 wynosi oznaczony jako β . Następnie wartości trygonometryczne dla pełnego kąta to , , i .
Wariant
Poniższy wariant wzoru Euklidesa jest czasami wygodniejszy, ponieważ jest bardziej symetryczny w m i n (ten sam warunek parzystości na m i n ).
Jeśli m i n są dwiema nieparzystymi liczbami całkowitymi takimi, że m > n , wtedy
są trzema liczbami całkowitymi, które tworzą trójkę pitagorejską, która jest pierwotna wtedy i tylko wtedy, gdy m i n są względnie pierwsze. Z drugiej strony, co powstaje potrójny prymitywny Pitagorasa (po wymianie i B , jeżeli nawet) z unikalną pary m > n > 0 o względnie pierwsze nieparzystych liczb całkowitych.
Podstawowe właściwości prymitywnych trójek pitagorejskich
Właściwości ogólne
Właściwości prymitywnej trójki pitagorejskiej ( a , b , c ) z a < b < c (bez określania, która z a lub b jest parzysta, a która nieparzysta) obejmują:
- jest zawsze idealnym kwadratem. Ponieważ jest to tylko warunek konieczny, ale niewystarczający, można go wykorzystać do sprawdzenia, czy dana trójka liczb nie jest trójką pitagorejską, gdy nie zda testu. Na przykład, każda trójka {6, 12, 18} i {1, 8, 9} przechodzi test, że ( c − a )( c − b )/2 jest idealnym kwadratem, ale żadna z nich nie jest trójką pitagorejską.
- Kiedy trójka liczb a , b i c tworzy pierwotną trójkę pitagorejską, wtedy ( c minus odnoga parzysta) i połowa ( c minus odnoga nieparzysta) są kwadratami idealnymi; nie jest to jednak warunek wystarczający, ponieważ liczby {1, 8, 9} przechodzą test idealnych kwadratów, ale nie są trójką pitagorejską, ponieważ 1 2 + 8 2 ≠ 9 2 .
- Co najwyżej jeden z a , b , c jest kwadratem.
- Pole trójkąta pitagorejskiego nie może być kwadratem lub dwukrotnością kwadratu liczby naturalnej.
- Dokładnie jeden z a , b jest podzielny przez 2 (jest parzysty ), ale nigdy c .
- Dokładnie jeden z a , b jest podzielny przez 3 , ale nigdy c .
- Dokładnie jeden z a , b jest podzielny przez 4, ale nigdy c (ponieważ c nigdy nie jest parzyste).
- Dokładnie jedno z a , b , c jest podzielne przez 5.
- Największa liczba, która zawsze dzieli abc, to 60.
- Dowolna liczba nieparzysta postaci 2 m +1 , gdzie m jest liczbą całkowitą, a m > 1 , może być nieparzystą odnogą pierwotnej trójki pitagorejskiej [PPT]. Zobacz sekcję prawie równoramiennego PPT poniżej. Jednak tylko liczby parzyste podzielne przez 4 mogą być parzystą nogą PPT. Dzieje się tak dlatego, że wzór Euklidesa na parzystą nogę podaną powyżej wynosi 2 min i jeden z m lub n musi być parzysty.
- Przeciwprostokątna c jest sumą dwóch kwadratów. Wymaga to, aby wszystkie jego czynniki pierwsze były liczbami pierwszymi postaci 4 n + 1 . Dlatego c ma postać 4 n + 1 . Sekwencję możliwych liczb przeciwprostokątnych dla PPT można znaleźć pod adresem (sekwencja A008846 w OEIS ).
- Pole ( K = ab /2) jest przystającą liczbą podzielną przez 6.
- W każdym trójkącie Pitagorasa, promień incircle i promienie trzech excircles są liczbami naturalnymi. W szczególności, dla prymitywnej trójki promień okręgu wynosi r = n ( m − n ) , a promienie eksokrętów przeciwległych do boków m 2 − n 2 , 2mn i przeciwprostokątnej m 2 + n 2 wynoszą odpowiednio m ( m - n ) , n ( m + n ) , i m ( m + n ) .
- Jak dla każdego trójkąta prostokątnego, odwrotność twierdzenia Talesa mówi, że średnica okręgu opisanego jest równa przeciwprostokątnej; stąd dla prymitywnych trójek średnica okręgu wynosi m 2 + n 2 , a promień okręgu jest połową tego, a zatem jest wymierny, ale nie jest liczbą całkowitą (ponieważ m i n mają przeciwną parzystość).
- Gdy pole trójkąta pitagorejskiego pomnożymy przez krzywizny jego okręgu i 3 eksokrętów, otrzymamy odpowiednio cztery dodatnie liczby całkowite w > x > y > z . Liczby całkowite − w , x , y , z spełniają równanie okręgu Kartezjusza . Równoważnie promień zewnętrznego okręgu Soddy'ego dowolnego trójkąta prostokątnego jest równy jego półobwodowi. Zewnętrzny ośrodek Soddy'ego znajduje się w D , gdzie ACBD jest prostokątem, ACB trójkątem prostokątnym, a AB jego przeciwprostokątną.
- Tylko dwie strony prymitywnej trójki pitagorejskiej mogą być jednocześnie pierwsze, ponieważ według wzoru Euklidesa na generowanie prymitywnej trójki pitagorejskiej jedna z nóg musi być złożona i równa. Jednak tylko jedna strona może być liczbą całkowitą o doskonałej potędze, ponieważ gdyby dwie strony były liczbami całkowitymi o doskonałych potęgach o równym wykładniku , byłoby to sprzeczne z faktem, że nie ma całkowitych rozwiązań równania diofantycznego , z , i będącymi parami względnie pierwszymi.
- Nie ma trójkątów pitagorejskich, w których przeciwprostokątna i jedna noga są odnogami innego trójkąta pitagorejskiego; jest to jedna z równoważnych postaci twierdzenia Fermata o trójkącie prostokątnym .
- Każdy prymitywny Pitagorasa trójkąta ma stosunek powierzchni, K do kwadratu semiperimeter , y , który jest przypisany do siebie i jest przez
- Żaden prymitywny trójkąt pitagorejski nie ma całkowitej wysokości od przeciwprostokątnej; to znaczy, że każdy prymitywny trójkąt pitagorejski jest nierozkładalny.
- Zbiór wszystkich prymitywnych trójek pitagorejskich tworzy w naturalny sposób ukorzenione drzewo trójskładnikowe ; zobacz Drzewo prymitywnych trójek pitagorejskich .
- Żaden z kątów ostrych trójkąta Pitagorasa może być liczbą wymierną od stopni . (Wynika to z twierdzenia Nivena .)
Przypadki specjalne
Ponadto można zagwarantować istnienie specjalnych trójek pitagorejskich o pewnych dodatkowych właściwościach:
- Każda liczba całkowita większa niż 2, która nie jest zgodna z 2 mod 4 (innymi słowy, każda liczba całkowita większa niż 2, która nie ma postaci 4 k + 2 ) jest częścią prymitywnej trójki pitagorejskiej. (Jeżeli całkowita ma postać 4 K może przyjąć n = 1 i m = 2, k we wzorze Euklidesa, jeżeli całkowita jest 2 K + 1 , można przyjąć n = k oraz m = k + 1 ).
- Każda liczba całkowita większa niż 2 jest częścią prymitywnej lub nieprymitywnej trójki pitagorejskiej. Na przykład liczby całkowite 6, 10, 14 i 18 nie są częścią pierwotnych trójek, ale są częścią nieprymitywnych trójek (6, 8, 10) , (14, 48, 50) i (18, 80, 82) .
- Istnieje nieskończenie wiele trójek pitagorejskich, w których przeciwprostokątna i najdłuższa noga różnią się dokładnie o jeden. Takie trójki są koniecznie prymitywne i mają postać (2 n + 1, 2 n 2 + 2 n , 2 n 2 + 2 n +1) . Wynika to ze wzoru Euklidesa, który zauważa, że warunek implikuje, że trójka jest pierwotna i musi zweryfikować ( m 2 + n 2 ) - 2 mn = 1 . To implikuje ( m – n ) 2 = 1 , a zatem m = n + 1 . Powyższa forma trójek powoduje zatem podstawienie m za n + 1 we wzorze Euklidesa.
- Istnieje nieskończenie wiele pierwotnych trójek pitagorejskich, w których przeciwprostokątna i najdłuższa noga różnią się dokładnie o dwa. Wszystkie są prymitywne i uzyskuje się je przez umieszczenie n = 1 we wzorze Euklidesa. Bardziej ogólnie, dla każdej liczby całkowitej k > 0 istnieje nieskończenie wiele pierwotnych trójek pitagorejskich, w których przeciwprostokątna i odnoga nieparzysta różnią się o 2 k 2 . Uzyskuje się je przez umieszczenie n = k we wzorze Euklidesa.
- Istnieje nieskończenie wiele trójek pitagorejskich, w których obie nogi różnią się dokładnie o jeden. Na przykład 20 2 + 21 2 = 29 2 ; są one generowane przez wzór Euklidesa, gdy jest zbieżny do √ 2 .
- Dla każdej liczby naturalnej k istnieje k trójek pitagorejskich o różnych przeciwprostokątnych i tej samej powierzchni.
- Dla każdej liczby naturalnej k istnieje co najmniej k różnych pierwotnych trójek pitagorejskich z tą samą nogą a , gdzie a jest pewną liczbą naturalną (długość parzystej nogi wynosi 2 mn , a wystarczy wybrać a z wieloma faktoryzacjami, na przykład a = 4 b , gdzie b jest iloczynem k różnych nieparzystych liczb pierwszych, co daje co najmniej 2 k różnych prymitywnych trójek).
- Dla każdej liczby naturalnej n istnieje co najmniej n różnych trójek pitagorejskich o tej samej przeciwprostokątnej.
- Istnieje nieskończenie wiele trójek pitagorejskich z liczbami kwadratowymi zarówno dla przeciwprostokątnej c , jak i sumy nóg a + b . Według Fermata najmniejsza taka trójka ma boki a = 4 565 486 027 761; b = 1 061 652 293 520; i c = 4 687 298 610 289. Tutaj + b = 2372159 2 i c = 2165017 2 . Jest to generowane przez wzór Euklidesa z wartościami parametrów m = 2 150 905 i n = 246 792.
- Istnieją nieprymitywne trójkąty pitagorejskie z całkowitą wysokością od przeciwprostokątnej . Takie trójkąty pitagorejskie są znane jako rozkładające się, ponieważ można je podzielić na tej wysokości na dwa oddzielne i mniejsze trójkąty pitagorejskie.
Geometria wzoru Euklidesa
Punkty wymierne na okręgu jednostkowym
Wzór Euklidesa na trójkę pitagorejską
można rozumieć w kategoriach geometrii punktów wymiernych na okręgu jednostkowym ( Trautman 1998 ).
W rzeczywistości punkt na płaszczyźnie kartezjańskiej o współrzędnych ( x , y ) należy do okręgu jednostkowego, jeśli x 2 + y 2 = 1 . Punkt jest wymierny, jeśli x i y są liczbami wymiernymi , to znaczy, jeśli istnieją liczby całkowite względnie pierwsze a , b , c takie, że
Mnożąc oba człony przez c 2 , można zobaczyć, że wymierne punkty na kole odpowiadają jeden do jednego z pierwotnymi trójkami pitagorejskimi.
Okrąg jednostkowy można również zdefiniować za pomocą równania parametrycznego
Wzór Euklidesa na trójki pitagorejskie oznacza, że z wyjątkiem (−1, 0) punkt na okręgu jest wymierny wtedy i tylko wtedy, gdy odpowiadająca mu wartość t jest liczbą wymierną.
Podejście stereograficzne

Istnieje zgodność między punktami na okręgu jednostkowym o wymiernych współrzędnych i prymitywnymi trójkami pitagorejskimi. W tym momencie wzory Euklidesa można wyprowadzić albo metodami trygonometrii, albo równoważnie przy użyciu rzutowania stereograficznego .
W podejściu stereograficznym załóżmy, że P ′ jest punktem na osi x o współrzędnych wymiernych
Wtedy można wykazać za pomocą podstawowej algebry, że punkt P ma współrzędne
Potwierdza to, że każdy racjonalny punkt z X -działający podchodzi do racjonalnego punktu okręgu jednostkowym. Odwrotność, że każdy wymierny punkt okręgu jednostkowego pochodzi z takiego punktu osi x , następuje przez zastosowanie odwrotnego rzutowania stereograficznego. Załóżmy, że P ( x , y ) jest punktem okręgu jednostkowego z liczbami wymiernymi x i y . Wtedy punkt P ′ uzyskany przez rzut stereograficzny na oś x ma współrzędne
co jest racjonalne.
Z punktu widzenia geometrii algebraicznej , algebraiczna różnorodność punktów wymiernych na okręgu jednostkowym jest biracjonalna do linii afinicznej nad liczbami wymiernymi. Okrąg jednostkowy nazywa się więc krzywą wymierną i to właśnie ten fakt umożliwia jednoznaczną parametryzację punktów (liczby wymiernej) na nim za pomocą funkcji wymiernych.
Trójkąty pitagorejskie w siatce 2D
Krata 2D to regularna tablica izolowanych punktów, w której jeśli dowolny punkt zostanie wybrany jako początek kartezjański (0, 0), to wszystkie pozostałe punkty znajdują się w ( x , y ) gdzie x i y obejmują wszystkie dodatnie i ujemne liczby całkowite . Dowolny trójkąt pitagorejski z potrójnym ( a , b , c ) może być narysowany w siatce 2D z wierzchołkami o współrzędnych (0, 0), ( a , 0) i (0, b ). Liczba punktów sieci leżących ściśle w granicach trójkąta jest dana przez dla prymitywnych trójek pitagorejskich ta liczba sieci wewnętrznej wynosi Powierzchnia (według twierdzenia Picka równa o jeden mniej niż liczba sieci wewnętrznej plus połowa liczby sieci granicznej) równa się .
Pierwsze wystąpienie dwóch prymitywnych trójek pitagorejskich dzielących ten sam obszar występuje z trójkątami o bokach (20, 21, 29), (12, 35, 37) i wspólnym obszarze 210 (sekwencja A093536 w OEIS ). Pierwsze wystąpienie dwóch prymitywnych trójek pitagorejskich o tej samej liczbie sieci wewnętrznej występuje z (18108, 252685, 253333), (28077, 162964, 165365) i liczbą sieci wewnętrznych 2287674594 (sekwencja A225760 w OEIS ). Znaleziono trzy prymitywne trójki pitagorejskie dzielące ten sam obszar: (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19019, 19069) z obszarem 13123110. Jak dotąd żaden zestaw trzech prymitywnych trójek pitagorejskich nie miał znaleziono dzielące tę samą liczbę wewnętrznych sieci.
Wyliczanie prymitywnych trójek pitagorejskich
Według wzoru Euklidesa wszystkie prymitywne trójki pitagorejskie mogą być generowane z liczb całkowitych oraz z , nieparzystymi i . Stąd istnieje odwzorowanie 1 do 1 wymiernych (w najniższych kategoriach) do prymitywnych trójek pitagorejskich, gdzie znajduje się w przedziale i jest nieparzyste.
Odwrotne odwzorowanie z prymitywnej trójki, gdzie do wymiernej osiąga się przez badanie dwóch sum i . Jedna z tych sum będzie kwadratem, który można zrównać, a druga będzie dwukrotnością kwadratu, który można zrównać z . Możliwe jest wtedy określenie racjonalności .
Aby wyliczyć prymitywne trójki pitagorejskie, wymierność można wyrazić jako uporządkowaną parę i odwzorować na liczbę całkowitą za pomocą funkcji parowania, takiej jak funkcja parowania Cantora . Przykład można zobaczyć na (sekwencja A277557 w OEIS ). Zaczyna
- i daje racjonalne podstawy
- te z kolei generują prymitywne trójki
Spinory i grupa modułowa
Trójki pitagorejskie można również zakodować w kwadratowej macierzy postaci
Macierz tej postaci jest symetryczna . Ponadto, czynnikiem decydującym o X jest
czyli dokładnie zero, gdy ( a , b , c ) jest trójką pitagorejską. Jeśli X odpowiada trójce pitagorejskiej, to jako macierz musi mieć rangę 1.
Ponieważ X jest symetryczny, z wyniku algebry liniowej wynika, że istnieje wektor kolumnowy ξ = [ m n ] T taki, że iloczyn zewnętrzny
-
( 1 )
trzyma, gdzie T oznacza transpozycję macierzy . Wektor ξ nazywamy spinorem (dla grupy Lorentza SO(1, 2)). Mówiąc abstrakcyjnie, wzór Euklidesa oznacza, że każda pierwotna trójka pitagorejska może być zapisana jako iloczyn zewnętrzny samego spinora z wpisami całkowitymi, jak w ( 1 ).
Grupa modularna Γ to zbiór macierzy 2×2 z wpisami całkowitymi
z wyznacznikiem równym jeden: αδ − βγ = 1 . Zbiór ten tworzy grupę , ponieważ odwrotność macierzy w Γ jest znowu w Γ, podobnie jak iloczyn dwóch macierzy w Γ. Grupa modularna działa na kolekcji wszystkich spinorów liczb całkowitych. Co więcej, grupa jest przechodnia w zbiorze spinorów liczb całkowitych ze względnie pierwszymi wpisami. Bo jeśli [ m n ] T ma wpisy względnie pierwsze, to
gdzie u i v są wybierane (przez algorytm Euklidesa ) tak, że mu + nv = 1 .
Działając na spinor ξ w ( 1 ), działanie Γ przechodzi do działania na trójki pitagorejskie, pod warunkiem, że dopuszcza się trójki z możliwie ujemnymi składowymi. Zatem jeśli A jest macierzą w Γ, to
-
( 2 )
powoduje działanie na macierz X w ( 1 ). Nie daje to dobrze zdefiniowanego działania na prymitywnych trójkach, ponieważ może zamienić prymitywną trójkę w prymitywną trójkę. Jest to wygodne, na tym etapie (na Trautmana 1998 ), aby potrójne ( , b , c ) standardu , czy c > 0 i albo ( , b , c ) jest względnie pierwsze lub ( / 2 b / 2, C / 2) są względnie pierwsze z / 2 dziwne. Jeżeli Spinor [ m n ] , T jest względnie pierwsze dane, a następnie wiąże się potrójne ( , b , c ) określona przez ( 1 ) jest standardowym potrójne. Wynika z tego, że działanie grupy modułowej jest przechodnie na zbiorze standardowych trójek.
Alternatywnie, ograniczający uwagę na tych wartościach m i n , dla których m jest liczbą nieparzystą, a N jest równe. Niech podgrupa Γ (2) o Tt jako jądro z homomorfizmu grupie
gdzie SL (2, Z 2 ) jest szczególną grupą liniowego na skończonego Z 2 z liczb modulo 2 . Wtedy Γ(2) jest grupą przekształceń unimodularnych, które zachowują parzystość każdego wpisu. Zatem jeśli pierwszy wpis ξ jest nieparzysty, a drugi parzysty, to to samo dotyczy A ξ dla wszystkich A ∈ Γ(2) . W rzeczywistości w ramach działania ( 2 ) grupa Γ(2) działa przejściowo na zbiór pierwotnych trójek pitagorejskich ( Alperin 2005 ).
Grupa Γ(2) to wolna grupa, której generatorami są macierze
W konsekwencji, każda prymitywny trójka pitagorejska może być uzyskana w unikalny sposób jako iloczyn kopii macierzy U i L .
Relacje rodzic/dziecko
W wyniku Berggrena (1934) wszystkie prymitywne trójki pitagorejskie można wygenerować z trójkąta (3, 4, 5) za pomocą trzech przekształceń liniowych T 1 , T 2 , T 3 poniżej, gdzie a , b , c są bokami trójki:
| nowa strona a | nowa strona b | nowa strona c | |
| T 1 : | a − 2 b + 2 c | 2 a − b + 2 c | 2 a − 2 b + 3 c |
| T 2 : | a + 2 b + 2 c | 2 a + b + 2 c | 2 + 2 b + 3 C |
| T 3 : | − a + 2 b + 2 c | -2 a + b + 2 c | -2 a + 2 b + 3 c |
Innymi słowy, każda pierwotna trójka będzie „rodzicem” trzech dodatkowych prymitywnych trójek. Zaczynając od początkowego węzła z a = 3, b = 4 i c = 5, operacja T 1 daje nową trójkę
- (3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5 , 12, 13),
i podobnie, T 2 i T 3 wytworzenia potrójne (21, 20, 29) oraz (15, 8, 17).
Przekształcenia liniowe T 1 , T 2 i T 3 mają interpretację geometryczną w języku form kwadratowych . Są one ściśle związane (ale nie są równe) odbicia generujące prostopadły grupę o x 2 + y 2 - Z 2 ciągu liczb całkowitych.
Stosunek do liczb całkowitych Gaussa
Alternatywnie, wzory Euklidesa mogą być analizowane i udowadniane przy użyciu liczb całkowitych Gaussa . Liczby całkowite Gaussa są liczbami zespolonymi postaci α = u + vi , gdzie u i v są zwykłymi liczbami całkowitymi , a i jest pierwiastkiem kwadratowym z liczby ujemnej . Te jednostki liczb całkowitych Gaussa są ± 1 i ± i. Zwykłe liczby całkowite nazywane są wymiernymi liczbami całkowitymi i oznaczane jako Z . Liczby całkowite Gaussa są oznaczone jako Z [ i ]. Prawa strona twierdzenia Pitagorasa może być uwzględniona w liczbach całkowitych Gaussa:
Prymitywny Pitagorasa potrójny jest taki, w którym i b są względnie pierwsze , to znaczy, mają nie czynniki pierwsze w liczbach. Dla takiej trójki albo a lub b jest parzyste, a drugie jest nieparzyste; z tego wynika, że c również jest nieparzyste.
Każdy z dwóch czynników z := a + bi i z* := a − bi pierwotnej trójki pitagorejskiej jest równy kwadratowi liczby całkowitej Gaussa. Można to udowodnić za pomocą właściwości, że każda liczba całkowita Gaussa może być jednoznacznie uwzględniona w gaussowskich liczbach pierwszych aż do jednostek . (Ta unikalna faktoryzacja wynika z faktu, że, mówiąc z grubsza, można na nich zdefiniować wersję algorytmu Euklidesa .) Dowód ma trzy kroki. Po pierwsze, jeśli a i b zakładowym głównymi czynnikami liczb całkowitych, potem także udostępniać żadnych czynniki pierwsze w Liczby całkowite Gaussa. (Załóżmy, że a = gu i b = gv z liczbami całkowitymi gaussowskimi g , u i v oraz g nie jest jednostką. Wtedy u i v leżą w tej samej linii przez początek. Wszystkie liczby całkowite gaussowskie na takim wierszu są całkowitymi wielokrotnościami pewnej liczby całkowitej gaussowskiej h . Ale wtedy liczba całkowita gh ≠ ±1 dzieli zarówno a i b .) Po drugie, z tego wynika, że z i z* również nie mają wspólnych czynników pierwszych w liczbach całkowitych Gaussa. Gdyby tak było, to ich wspólny dzielnik δ również podzieliłby z + z* = 2 a oraz z − z* = 2 ib . Ponieważ a i b są względnie pierwsze, oznacza to, że δ dzieli 2 = (1 + i)(1 − i) = i(1 − i) 2 . Ze wzoru c 2 = zz* , to z kolei oznaczałoby, że c jest parzyste, wbrew hipotezie o prymitywnej trójce pitagorejskiej. Po trzecie, ponieważ c 2 jest kwadratem, każdy w swoim prime Gaussa faktoryzacji jest podwojona, czyli pojawia się numer, nawet wielokrotnie. Ponieważ z i z* nie mają wspólnych czynników pierwszych, to podwojenie jest również prawdziwe dla nich. Stąd z i z* są kwadratami.
W ten sposób można zapisać pierwszy czynnik
Rzeczywiste i urojone części tego równania dają dwie formuły:
Dla każdego prymitywnego Pitagorasa potrójne, nie musi być całkowite m i n takie, że te dwa równania są spełnione. Dlatego każda trójka pitagorejska może zostać wygenerowana z pewnego wyboru tych liczb całkowitych.
Jako idealne kwadratowe liczby całkowite Gaussa
Jeśli rozważymy kwadrat liczby całkowitej Gaussa, otrzymamy następującą bezpośrednią interpretację wzoru Euklidesa jako reprezentującego idealny kwadrat liczby całkowitej Gaussa.
Korzystając z faktu, że liczby całkowite Gaussa są domeną euklidesową i że dla liczby całkowitej Gaussa p jest zawsze kwadratem, można wykazać, że trójka pitagorejska odpowiada kwadratowi liczby całkowitej Gaussa, jeśli przeciwprostokątna jest liczbą pierwszą.
Jeśli liczba całkowita Gaussa nie jest liczbą pierwszą, to jest iloczynem dwóch liczb całkowitych gaussowskich p i q z liczbami całkowitymi i . Ponieważ wielkości mnożą się w liczbach całkowitych Gaussa, iloczyn musi być równy , który po podniesieniu do kwadratu, aby znaleźć trójkę pitagorejską, musi być złożony. Przeciwstawność uzupełnia dowód.
Stosunek do elips o wymiarach całkowitych
W odniesieniu do figury i definicji ognisk elipsy F 1 i F 2 , dla dowolnego punktu P na elipsy F 1 P + PF 2 jest stała.
Ponieważ oba punkty A i B leżą na elipsie, F 1 A + AF 2 = F 1 B + BF 2 . Ze względu na symetrię F 1 A + AF 2 = F 2 A' + AF 2 = AA' = 2 AC i F 1 B + BF 2 = 2 BF 2 . Stąd AC = BF 2 .
Tak więc, jeśli BCF 2 jest trójkątem prostokątnym z integralnymi bokami, oddzielenie ognisk, mimośrodowość liniowa, oś mała i oś główna są również liczbami całkowitymi.
Rozkład trójek
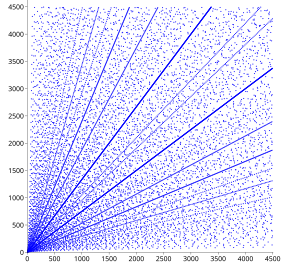
Istnieje wiele wyników dotyczących rozmieszczenia trójek pitagorejskich. Na wykresie punktowym widać już szereg oczywistych wzorów. Ilekroć na wykresie pojawiają się odnogi ( a , b ) prymitywnej trójki, wszystkie całkowite wielokrotności ( a , b ) muszą również pojawić się na wykresie, a ta właściwość powoduje pojawienie się linii wychodzących z początku wykresu.
W rozproszeniu znajdują się zestawy parabolicznych wzorów o dużej gęstości punktów i wszystkich ich ognisk w punkcie początkowym, otwierających się we wszystkich czterech kierunkach. Różne parabole przecinają się w osiach i wydają się odbijać od osi pod kątem padania 45 stopni, przy czym trzecia parabola wchodzi prostopadle. W tym kwadrancie każdy łuk wyśrodkowany na początku pokazuje tę część paraboli, która leży między jej wierzchołkiem a jej przecięciem z odbytnicą półlatusa .
Te wzorce można wyjaśnić w następujący sposób. Jeśli jest liczbą całkowitą, to ( a , , ) jest potrójną pitagorejską. (W rzeczywistości każda trójka pitagorejska ( a , b , c ) może być zapisana w ten sposób z liczbą całkowitą n , prawdopodobnie po zamianie a i b , ponieważ i a i b nie mogą być oba nieparzyste.) Trójki pitagorejskie leżą zatem na krzywych podanych przez , czyli parabole odbijana na -osiowy i odpowiednie krzywe z i b zamienione. Jeśli a jest zmienne dla danego n (tj. na danej paraboli), wartości całkowite b występują stosunkowo często, jeśli n jest kwadratem lub małą wielokrotnością kwadratu. Jeśli kilka takich wartości zdarzy się leżeć blisko siebie, odpowiadające im parabole w przybliżeniu się pokrywają, a trójki grupują się w wąski pas paraboliczny. Na przykład 38 2 = 1444, 2 x 27 2 = 1458, 3 x 22 2 = 1452, 5 x 17 2 = 1445 i 10 x 12 2 = 1440; odpowiedni pas paraboliczny wokół n 1450 jest wyraźnie widoczny na wykresie punktowym.
Opisane powyżej właściwości kątowe wynikają bezpośrednio z funkcjonalnej formy paraboli. Parabole są odbite na osi a przy a = 2 n , a pochodna b względem a w tym punkcie wynosi –1; stąd kąt padania wynosi 45°. Ponieważ skupienia, podobnie jak wszystkie trójki, powtarzają się jako całkowite wielokrotności, wartość 2 n również odpowiada skupieniu. Odpowiednia parabola przecina oś b pod kątem prostym w b = 2 n , a zatem jej odbicie po zamianie a i b przecina oś a pod kątem prostym w a = 2 n , dokładnie tam, gdzie parabola dla n jest odbijana w -działający. (To samo dotyczy zamienionych liter a i b ).
Albert Fässler i inni dostarczają wglądu w znaczenie tych parabol w kontekście mapowań konforemnych.
Sekwencja platońska
Przypadek n = 1 bardziej ogólnej konstrukcji trójek pitagorejskich jest znany od dawna. Proklos , w swoim komentarzu do twierdzenia 47th pierwszej księgi Euklidesa Elementy , opisuje to w następujący sposób:
Pewne metody odkrywania tego rodzaju trójkątów są przekazywane, jedną, którą odnoszą do Platona, a drugą do Pitagorasa . (Ten ostatni) zaczyna się od liczb nieparzystych. To sprawia, że liczba nieparzysta jest mniejsza z boków pod kątem prostym; następnie bierze jej kwadrat, odejmuje jedność i robi połowę różnicy większy z boków pod kątem prostym; wreszcie dodaje jedności do tego i tworzy pozostałą stronę, przeciwprostokątną.
... Albowiem metoda Platona argumentuje z parzystych liczb. Pobiera podaną liczbę parzystą i czyni ją jednym z boków pod kątem prostym; następnie, dzieląc tę liczbę na pół i podnosząc do kwadratu połowę, dodaje jedność do kwadratu, tworząc przeciwprostokątną, i odejmuje jedność od kwadratu, tworząc drugą stronę pod kątem prostym. ... W ten sposób utworzyła ten sam trójkąt, który uzyskano inną metodą.
W postaci równania staje się to:
a jest nieparzyste (Pythagoras, ok. 540 pne):
a jest parzyste (Platon, ok. 380 pne):
Można wykazać, że wszystkie trójki pitagorejskie można uzyskać, przy odpowiednim przeskalowaniu, z podstawowego ciągu platońskiego ( a , ( a 2 − 1)/2 i ( a 2 + 1)/2 ), pozwalając a na przyjęcie liczby niecałkowitej wartości racjonalne. Jeśli a zostanie zastąpione ułamkiem m / n w sekwencji, wynik jest równy „standardowemu” potrójnemu generatorowi (2 mn , m 2 − n 2 , m 2 + n 2 ) po przeskalowaniu. Wynika z tego, że każdy posiada odpowiedni potrójne racjonalne jest wartość, która może być użyta do wytworzenia podobnego trójkąta (jedna z tych samych trzech kątów i z boków w tych samych proporcjach jak w oryginale). Na przykład odpowiednik platoński (56, 33, 65) jest generowany przez a = m / n = 7/4 jako ( a , ( a 2 –1)/2, ( a 2 +1)/2) = ( 56/32, 33/32, 65/32). Sama sekwencja platońska może być wyprowadzona przez wykonanie kroków „podziału kwadratu” opisanych w Diophantus II.VIII .
Równanie Jacobiego-Maddena
Równanie,
jest odpowiednikiem specjalnej trójki pitagorejskiej,
Istnieje nieskończona liczba rozwiązań tego równania, ponieważ rozwiązywanie zmiennych obejmuje krzywą eliptyczną . Małe są,
Równe sumy dwóch kwadratów
Jednym ze sposobów generowania rozwiązań jest parametryzacja a, b, c, d w postaci liczb całkowitych m, n, p, q w następujący sposób:
Równe sumy dwóch czwartych potęg
Biorąc pod uwagę dwa zestawy trójek pitagorejskich,
problem znalezienia równych iloczynów strony nie przeciwprostokątnej i przeciwprostokątnej,
łatwo zauważyć, że jest równoważny równaniu,
i został po raz pierwszy rozwiązany przez Eulera jako . Ponieważ pokazał, że jest to punkt wymierny na krzywej eliptycznej , to istnieje nieskończona liczba rozwiązań. W rzeczywistości znalazł również parametryzację wielomianu 7 stopnia.
Twierdzenie Kartezjusza o okręgu
W przypadku twierdzenia Kartezjusza o okręgu, w którym wszystkie zmienne są kwadratami,
Euler wykazał, że jest to równoważne trzem równoczesnym trójkom pitagorejskim,
Istnieje również nieskończona liczba rozwiązań, a dla szczególnego przypadku, gdy , równanie upraszcza się do,
z małymi rozwiązaniami jak i mogą być rozwiązywane jako binarne formy kwadratowe .
Prawie równoramienne trójki pitagorejskie
Potrójne nie pitagorejską są równoramiennego , ponieważ stosunek przeciwprostokątnej do jednej drugiej strony jest √ 2 , ale √ 2 nie może być wyrażona jako stosunek 2 całkowitymi .
Istnieją jednak trójkąty prostokątne z integralnymi bokami, dla których długości boków nie przeciwprostokątnych różnią się o jeden, takie jak:
i nieskończoną liczbę innych. Można je całkowicie sparametryzować jako,
gdzie { x,y } są rozwiązaniami równania Pella .
Jeśli a , b , c są bokami tego typu prymitywnej trójki pitagorejskiej (PPT), to rozwiązanie równania Pella jest podane za pomocą wzoru rekurencyjnego
- z i
- z i
- z i .
Ta sekwencja PPT tworzy centralny pień (pień) ukorzenionego drzewa trójskładnikowego PPT.
Gdy dłuższa strona bez przeciwprostokątnej i przeciwprostokątna różnią się o jeden, na przykład in
to kompletne rozwiązanie dla PPT a , b , c to
oraz
gdzie liczba całkowita jest parametrem generującym.
Pokazuje, że wszystkie liczby nieparzyste (większe niż 1) pojawiają się w tego typu prawie równoramiennym PPT. Ta sekwencja PPT tworzy po prawej stronie zewnętrzny pień ukorzenionego drzewa trójskładnikowego PPT.
Inną właściwością tego typu prawie równoramiennych PPT jest to, że boki są powiązane w taki sposób, że
dla jakiejś liczby całkowitej . Innymi słowy jest podzielna przez takie jak in
- .
Liczby Fibonacciego w trójkach pitagorejskich
Zaczynając od 5, co druga liczba Fibonacciego jest długością przeciwprostokątnej trójkąta prostokątnego o bokach całkowitych, czyli największą liczbą w trójce pitagorejskiej, otrzymaną ze wzoru
- (3,4,5), (5,12,13), (16,30,34), (39,80,89), ...
Środkowy bok każdego z tych trójkątów jest sumą trzech boków poprzedniego trójkąta.
Uogólnienia
Istnieje kilka sposobów na uogólnienie koncepcji trójek pitagorejskich.
pitagorejski n -krotka
Używając prostej tożsamości algebraicznej ,
dla dowolnych x 0 , x 1 , łatwo jest udowodnić, że kwadrat sumy n kwadratów jest sam w sobie sumą n kwadratów, pozwalając x 0 = x 2 2 + x 3 2 + ... + x n 2 i następnie dystrybucja warunków. Można zobaczyć, jak pitagorejskie trójki i czwórki są tylko konkretnymi przypadkami odpowiednio x 0 = x 2 2 i x 0 = x 2 2 + x 3 2 , i tak dalej dla innych n , z pięciokrotnymi danymi przez
Ponieważ suma F ( k , m ) k kolejnych kwadratów zaczynających się od m 2 jest dana wzorem:
można znaleźć wartości ( k , m ) tak, że F ( k , m ) jest kwadratem, np. Hirschhorna, gdzie sama liczba wyrazów jest kwadratem,
a v ≥ 5 jest dowolną liczbą całkowitą niepodzielną przez 2 lub 3. Dla najmniejszego przypadku v = 5, stąd k = 25, daje to dobrze znany problem Lucasa układania kul armatnich ,
fakt, który jest związany z siecią Leech .
Dodatkowo, jeśli w n- krotce pitagorejskiej ( n ≥ 4) wszystkie dodatki są kolejne z wyjątkiem jednego, można użyć równania,
Ponieważ druga potęga p znosi się, jest to tylko liniowe i łatwe do rozwiązania, tak jakby k , m powinno być wybrane tak, że p jest liczbą całkowitą, z małym przykładem k = 5, m = 1, co daje,
Tak więc jednym ze sposobów generowania pitagorejskich n -krotek jest użycie dla różnych x ,
gdzie q = n –2 i gdzie
Czteroosobowy pitagorejski
Zbiór czterech dodatnich liczb całkowitych a , b , c i d takich , że a 2 + b 2 + c 2 = d 2 jest nazywany czwórką pitagorejską . Najprostszym przykładem jest (1, 2, 2, 3), ponieważ 1 2 + 2 2 + 2 2 = 3 2 . Następnym najprostszym (prymitywnym) przykładem jest (2, 3, 6, 7), ponieważ 2 2 + 3 2 + 6 2 = 7 2 .
Wszystkie czwórki są podane wzorem
Wielkie Twierdzenie Fermata
Uogólnienie koncepcji Pitagorasa potrójne jest poszukiwanie trójek dodatnich liczb całkowitych , b i c tak, że n + b n = c n jakiegoś n większy od 2. Pierre de Fermatem w 1637 twierdził, że nie taka trójka istnieje, twierdzenie, które stało się znane jako Wielkie Twierdzenie Fermata, ponieważ jego udowodnienie lub obalenie zajęło więcej czasu niż jakiekolwiek inne przypuszczenie Fermata. Pierwszy dowód dał Andrew Wiles w 1994 roku.
n − 1 lub n n- te potęgi sumujące się do n- tej potęgi
Innym uogólnieniem jest poszukiwanie ciągów n +1 dodatnich liczb całkowitych, dla których n- ta potęga ostatniej jest sumą n- tej potęgi poprzednich wyrazów. Najmniejsze ciągi dla znanych wartości n to:
- n = 3: {3, 4, 5; 6}.
- n = 4: {30, 120, 272, 315; 353}
- n = 5: {19, 43, 46, 47, 67; 72}
- n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
- n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}
Dla przypadku n =3, w którym nazwano sześcienny Fermata , istnieje ogólna formuła podająca wszystkie rozwiązania.
Nieco inne uogólnienie pozwala, aby suma ( k + 1) n-tych potęg była równa sumie ( n − k ) n-tych potęg. Na przykład:
- ( n = 3): 1 3 + 12 3 = 9 3 + 10 3 , rozsławiona wspomnieniami Hardy'ego o rozmowie z Ramanujanem o liczbie 1729 jako najmniejszej liczbie, którą można wyrazić jako sumę dwóch sześcianów na dwa różne sposoby .
Może również istnieć n − 1 dodatnich liczb całkowitych, których n- te potęgi sumują się do n- tej potęgi (chociaż według Wielkiego Twierdzenia Fermata nie dla n = 3); są to kontrprzykłady do przypuszczeń Eulera o sumie potęg . Najmniejsze znane kontrprzykłady to
- n = 4: (95800, 217519, 414560; 422481)
- n = 5: (27, 84, 110, 133; 144)
Trójka heronowskich trójkątów
Heronian trójkąt jest powszechnie definiowany jako jeden z boków całkowitą, której powierzchnia jest liczbą całkowitą, i jest uważamy Heronian trójkątów z różnych stron całkowitych. Długości boków takiego trójkąta tworzą trójkę heronową ( a, b, c ) pod warunkiem a < b < c . Każda trójka pitagorejska jest trójką herońską, ponieważ przynajmniej jedna z nóg a , b musi być parzysta w trójce pitagorejskiej, więc obszar ab /2 jest liczbą całkowitą. Jednak nie każda trójka herona jest trójką pitagorejską, jak pokazuje przykład (4, 13, 15) z obszarem 24.
Jeśli ( a , b , c ) jest trójką herońską, tak samo jest z ( ma , mb , mc ) gdzie m jest dowolną dodatnią liczbą całkowitą; jego pole będzie liczbą całkowitą, która jest m 2 razy większa od powierzchni całkowitej trójkąta ( a , b , c ) . Trójka herona ( a , b , c ) jest pierwotna pod warunkiem , że a , b , c są względnie pierwsze . (W przypadku prymitywnych trójek pitagorejskich obowiązuje również silniejsze zdanie, że są one parami względnie pierwsze, ale w przypadku prymitywnych trójkątów herońskich silniejsze zdanie nie zawsze jest prawdziwe, na przykład with (7, 15, 20)) . Trójki heronowe, które nie są trójkami pitagorejskimi:
- (4, 13, 15) o pow. 24
- (3, 25, 26) o pow. 36
- (7, 15, 20) o pow. 42
- (6, 25, 29) o pow. 60
- (11, 13, 20) o pow. 66
- (13, 14, 15) o pow. 84
- (13, 20, 21) o pow. 126
Zgodnie ze wzorem Herona dodatkowym warunkiem dla potrójnej liczby dodatnich liczb całkowitych ( a , b , c ) gdzie a < b < c jest heron jest to
- ( a 2 + b 2 + c 2 ) 2 − 2( a 4 + b 4 + c 4 )
lub równoważnie
- 2( a 2 b 2 + a 2 c 2 + b 2 c 2 ) − ( a 4 + b 4 + c 4 )
być niezerowym idealnym kwadratem podzielnym przez 16.
Zastosowanie do kryptografii
Prymitywne trójki pitagorejskie były używane w kryptografii jako sekwencje losowe i do generowania kluczy.
Zobacz też
- Problem trójek Boole'a Pitagorasa
- Congruum
- Diofant II.VIII
- Potrójny Eisenstein
- Cegła Eulera
- Trójkąt Heroński
- Twierdzenie Hilberta 90
- Trójkąt całkowity
- Arytmetyka modułowa
- Numer bez hipotensji
- Plimpton 322
- Pierwsza liczba pitagorejska
- Czteroosobowy pitagorejski
- Formuła półkąta stycznego
- Tożsamość trygonometryczna
Uwagi
Bibliografia
- Alperin, Roger C. (2005), "Modułowe drzewo Pitagorasa" (PDF) , American Mathematical Monthly , 112 (9): 807-816, CiteSeerX 10.1.1.112.3085 , doi : 10.2307/30037602 , JSTOR 30037602 , MR 2179860
- Berggren, B. (1934), "Pytagoreiska trianglar", Tidskrift for Elementär Matematik, Fysik i Kemi (w języku szwedzkim), 17 : 129-139
- Barning, FJM (1963), "Ponad pitagorese en bijna-pythagorese driehoeken en een generatieproces z behulp van unimodulaire matrices" (PDF) , Math. Centrum Amsterdamu Afd. Zuivere Wisk. (w języku niderlandzkim), ZW-011: 37
- Eckert, Ernest (1992), "Prymitywny pitagorejski trójki", The College Mathematics Journal , 23 (5): 413-417, doi : 10.2307/2686417 , JSTOR 2686417
- Elkies, Noam , trójki pitagorejskie i twierdzenie Hilberta 90 (PDF)
- Heath, Thomas (1956), Trzynaście ksiąg o elementach Euklidesa tom. 1 (Księgi I i II) (2nd ed.), Dover Publications, ISBN 978-0-486-60088-8
- Long, Calvin T. (1972), Elementary Wprowadzenie do teorii liczb (2nd ed.), Lexington: DC Heath and Company , LCCN 77171950
- Martin, Artemas (1875), „Racjonalne trójkąty prostokątne prawie równoramienne”, The Analyst , 3 (2): 47-50, doi : 10.2307/2635906 , JSTOR 2635906
- McCullough, Darryl (2005), "Wysokość i nadmiar trójek pitagorejskich" (PDF) , Magazyn Matematyka , 78 (1): 26-44, doi : 10.1080/0025570X.2005.11953298 , S2CID 1701449
- Romik, Dan (2008), „Dynamika trójek pitagorejskich” (PDF) , przeł. Amer. Matematyka. Soc. , 360 (11): 6045–6064, arXiv : math.DS/0406512 , doi : 10.1090/S0002-9947-08-04467-X , MR 2425702
- Teigen, MG; Hadwin, DW (1971), "O generowaniu trójek pitagorejskich", The American Mathematical Monthly , 78 (4): 378-379, doi : 10.2307/2316903 , JSTOR 2316903
- Trautman, Andrzej (1998), „Pythagorean spinors i Penrose twistors” , w SA Hugget; LJ Mason; KP Tod; ST Tsou; NMJ Woodhouse (red.), Geometryczny wszechświat (postscript)
Zewnętrzne linki
- Algebry Clifforda i parametryzacja trójek pitagorejskich Euklidesa
- Ciekawe konsekwencje błędnie skopiowanego kwadratu
- Omówienie właściwości trójek pitagorejskich, interaktywnych kalkulatorów, zagadek i problemów
- Generowanie trójek pitagorejskich za pomocą progresji arytmetycznych
- „Liczby pitagorejskie” , Encyklopedia Matematyki , EMS Press , 2001 [1994]
- Interaktywny kalkulator trójek pitagorejskich
- Ujemne równanie Pella i trójki pitagorejskie
- Parametryzacja trójek pitagorejskich przez pojedynczą trójkę wielomianów
- Price, H. Lee (2008), "Drzewo pitagorejskie: nowy gatunek", arXiv : 0809.4324 [ math.HO ]
- Trójki pitagorejskie i koło jednostkowe , rozdz. 2-3, w „ Przyjazne wprowadzenie do teorii liczb ” Josepha H. Silvermana, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9
- Trójki pitagorejskie w interaktywnym aplecie typu cut-the-knot pokazujące relacje w okręgach jednostkowych z trójkami pitagorejskimi
- Trójki pitagorejskie
- Niezwykłe koło trójkąta
- Rozwiązania dla par zgodnych z kwadratem w odniesieniu do trójek pitagorejskich
- Teoretyczne własności trójek pitagorejskich i związki z geometrią
- Drzewo trójdzielne leżące u podstaw prymitywnych trójek pitagorejskich na przecięciu węzła
- Weisstein, Eric W. „Trójka pitagorejska” . MatematykaŚwiat .

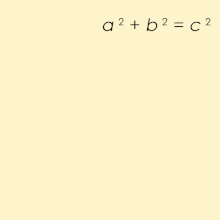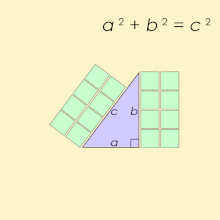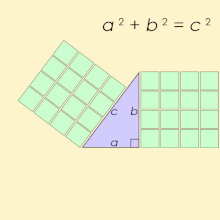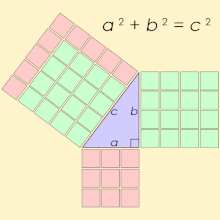




























































![X=2{\begin{bmatryca}m\\n\end{bmatryca}}[m\ n]=2\xi \xi ^{T}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/248a4dd30e8590ddf33a9f53d452656dff6711ec)









































































