Klasyfikacja Bianchi - Bianchi classification

W matematyce , klasyfikacja Bianchi zawiera listę wszystkich prawdziwych 3-wymiarowych algebr Lie ( do izomorfizmu ). Klasyfikacja zawiera 11 klas, z których 9 zawiera pojedynczą algebrę Liego, a dwie z nich zawierają rodzinę algebr Liego o wielkości kontinuum. (Czasami dwie grupy są zawarte w nieskończonych rodzinach, dając 9 zamiast 11 klas.) Klasyfikacja jest ważna w geometrii i fizyce, ponieważ powiązane grupy Liego służą jako grupy symetrii trójwymiarowych rozmaitości riemannowskich . Jego nazwa pochodzi od Luigiego Bianchi , który opracował go w 1898 roku.

Termin „klasyfikacja Bianchi” jest również używany do podobnych klasyfikacji w innych wymiarach oraz do klasyfikacji złożonych algebr Liego .

Klasyfikacja w wymiarze mniejszym niż 3

• Wymiar 0: Jedyna algebra Liego to abelowa algebra Liego R ⁰ .
• Wymiar 1: Jedyna algebra Liego to abelowa algebra Liego R ¹ , z zewnętrzną grupą automorfizmu multiplikatywną grupą niezerowych liczb rzeczywistych.
• Wymiar 2: Istnieją dwie algebry Liego:
  • (1) Abelowa algebra Liego R ² , z zewnętrzną grupą automorfizmu GL ₂ ( R ) .
  • (2) Rozwiązalna algebra Liego o 2×2 górnych trójkątnych macierzach śladu 0. Ma trywialne centrum i trywialną zewnętrzną grupę automorfizmu. Związane po prostu połączone grupy Lie jest afiniczne grupa linii.

Klasyfikacja w wymiarze 3

Wszystkie 3-wymiarowej Lie algebrami innego typu niż VIII i IX, może być wykonana jako iloczynów produktu z R ² i R , a R działający w R ^2, przez około 2 o 2 macierzy M . Różne typy odpowiadają różnym typom macierzy M , jak opisano poniżej.

• Typ I : Jest to abelowa i jednomodułowa algebra Liego R ³ . Grupa połączona prosto ma centrum R ³ i zewnętrzną grupę automorfizmu GL ₃ ( R ). Dzieje się tak, gdy M wynosi 0.
• Typ II : Algebra Heisenberga , która jest nilpotentna i jednomodułowa. Grupa połączona prosto ma centrum R i zewnętrzną grupę automorfizmu GL ₂ ( R ). Dzieje się tak, gdy M jest nilpotentny, ale nie 0 (wartości własne wszystkie 0).
• Typ III : Ta algebra jest iloczynem R i dwuwymiarowej nieabelowej algebry Liego. (Jest to przypadek graniczny typu VI, w którym jedna wartość własna staje się zerem). Jest rozwiązywalny i nie jest unimodularny. Grupa połączona prostopadle ma centrum R, a zewnętrzną grupę automorfizmu grupę niezerowych liczb rzeczywistych. Macierz M ma jedną zerową i jedną niezerową wartość własną.
• Typ IV : Algebra wygenerowana przez [ y , z ] = 0 , [ x , y ] = y , [ x , z ] = y + z . Jest rozwiązywalny i nie jednomodułowy. Grupa połączona prostopadle ma trywialny środek i zewnętrzną grupę automorfizmu iloczynu liczb rzeczywistych i grupę rzędu 2. Macierz M ma dwie równe niezerowe wartości własne, ale nie jest diagonalizowalna .
• Wpisz V : [ y , z ] = 0 , [ x , y ] = y , [ x , z ] = z . Rozwiązalny i nie jednomodułowy. (Przypadek graniczny typu VI, w którym obie wartości własne są równe.) Prosto połączona grupa ma trywialne centrum i zewnętrzną grupę automorfizmu elementy GL ₂ ( R ) wyznacznika +1 lub -1. Macierz M ma dwie równe wartości własne i jest diagonalizowalna.
• Typ VI : Nieskończona rodzina: półpośrednie iloczyny R ² przez R , gdzie macierz M ma niezerowe odrębne rzeczywiste wartości własne o sumie niezerowej. Algebry są rozwiązywalne, a nie unimodularne. Grupa połączona prostopadle ma trywialny środek i zewnętrzną grupę automorfizmu iloczynu niezerowych liczb rzeczywistych i grupy rzędu 2.
• Typu VI ₀ : leżeć Algebra jest iloczynów iloczyn R ² o R , z R , gdzie macierz M musi niezerowe różne rzeczywistych wartości własnych o sumie zerowej. Jest rozwiązywalny i jednomodułowy. Jest to algebra Liego dwuwymiarowej grupy Poincarégo , grupy izometrii dwuwymiarowej przestrzeni Minkowskiego . Grupa połączona prostopadle ma trywialny środek i zewnętrzną grupę automorfizmu iloczynu dodatnich liczb rzeczywistych z grupą dwuścienną rzędu 8.
• Typ VII : Nieskończona rodzina: półbezpośrednie produkty R ² przez R , gdzie macierz M ma nierzeczywiste i nieurojone wartości własne. Rozwiązalny i nie jednomodułowy. Prosto połączona grupa ma trywialne centrum i zewnętrzną grupę automorfizmu niezerowe liczby rzeczywiste.
• Typ VII ₀ : Półpośredni iloczyn R ² przez R , gdzie macierz M ma niezerowe urojone wartości własne. Rozwiązalny i jednomodułowy. To jest algebra Liego grupy izometrii płaszczyzny. Grupa połączona prostopadle ma centrum Z i zewnętrzną grupę automorfizmu, będącą iloczynem niezerowych liczb rzeczywistych i grupy rzędu 2.
• Typ VIII : Algebra Liego sl ₂ ( R ) bezśladowych macierzy 2 na 2, związanych z grupą SL ₂ (R) . To jest proste i jednomodułowe. Prosto połączona grupa nie jest grupą macierzową; jest oznaczony przez , ma centrum Z, a jego zewnętrzna grupa automorfizmu ma rząd 2.${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R})}}}$
• Typ IX : Algebra Liego grupy ortogonalnej O ₃ ( R ). Jest oznaczony przez 𝖘𝖔(3) i jest prosty i jednomodułowy. Odpowiednia prosta połączona grupa to SU(2) ; ma środek rzędu 2 i trywialną zewnętrzną grupę automorfizmu i jest grupą spinową .

Klasyfikacja trójwymiarowych złożonych algebr Liego jest podobna, z tym wyjątkiem, że typy VIII i IX stają się izomorficzne, a typy VI i VII stają się częścią jednej rodziny algebr Liego.

Połączone trójwymiarowe grupy Liego można sklasyfikować w następujący sposób: są one ilorazem odpowiedniej prostej połączonej grupy Liego przez dyskretną podgrupę środka, więc można je odczytać z powyższej tabeli.

Grupy są powiązane z 8 geometriami hipotezy geometryzacyjnej Thurstona . Dokładniej, siedem z ośmiu geometrii może być zrealizowanych jako metryka lewostronna w po prostu połączonej grupie (czasem na więcej niż jeden sposób). Geometria Thurstona typu S ² × R nie może być zrealizowana w ten sposób.

Stałe struktury

Każda z trójwymiarowych przestrzeni Bianchiego zawiera zestaw trzech pól wektorów zabijania, które mają następującą własność: ${\ Displaystyle \ xi _ {i} ^ {(a)}}$

${\ Displaystyle \ lewo ({\ Frac {\ częściowy \ xi _ {i} ^ {(c)}} {\ częściowy x ^ {k}}} - {\ Frac {\ częściowy \ X _ {k} ^ { (c)}}{\częściowy x^{i}}}\right)\xi _{(a)}^{i}\xi _{(b)}^{k}=C_{\ ab}^{ do}}$

gdzie „stałe strukturalne” grupy tworzą antysymetryczny tensor o stałym rzędzie-trzy w dwóch dolnych indeksach. Dla dowolnej trójwymiarowej przestrzeni Bianchiego dana jest relacja ${\ Displaystyle C_ {\ ab} ^ {c}}$ ${\ Displaystyle C_ {\ ab} ^ {c}}$

${\ Displaystyle C_ {\ ab} ^ {c} = \ varepsilon _ {abd} n ^ {cd} - \ delta _ {a} ^ {c} a_ {b} + \ delta _ {b} ^ {c} a_{a}}$

gdzie jest symbolem Levi Civita , jest trójkąt Kronecker i wektor i przekątna napinacz opisano w poniższej tabeli, w którym podana jest I th wartości własnych w ; parametr a przebiega przez wszystkie dodatnie liczby rzeczywiste : ${\ Displaystyle \ varepsilon _ {abd}}$${\ Displaystyle \ delta _ {a} ^ {c}}$${\ Displaystyle a_ {a} = (a, 0,0)}$${\ Displaystyle n ^ {cd}}$${\ Displaystyle n ^ {(i)}}$${\ Displaystyle n ^ {cd}}$

Typ Bianchi	${\displaystyle a}$	${\ Displaystyle n ^ {(1)}}$	${\ Displaystyle n ^ {(2)}}$	${\ Displaystyle n ^ {(3)}}$	klasa	notatki	graficzny (rys. 1)
ja	0	0	0	0	ZA	opisuje przestrzeń euklidesową	na początku
II	0	1	0	0	ZA		interwał [0,1] wzdłuż ${\ Displaystyle n ^ {(1)}}$
III	1	0	1	-1	b	podprzypadek typu VI a z${\displaystyle a=1}$	rzuty na czwartą ćwiartkę płaszczyzny a = 0
IV	1	0	0	1	b		pionowa otwarta powierzchnia między pierwszą a czwartą ćwiartką płaszczyzny a = 0
V	1	0	0	0	b	ma hiperpsosferę jako przypadek szczególny	przedział (0,1] wzdłuż osi a
VI 0	0	1	-1	0	ZA		czwarty kwadrant płaszczyzny poziomej
VI a	${\displaystyle a}$	0	1	-1	b	kiedy , odpowiednik typu III${\displaystyle a=1}$	rzuty na czwartą ćwiartkę płaszczyzny a = 0
VII 0	0	1	1	0	ZA	ma przestrzeń euklidesową jako szczególny przypadek	pierwsza ćwiartka płaszczyzny poziomej
VII a	${\displaystyle a}$	0	1	1	b	ma hiperpseudosferę jako szczególny przypadek	rzutuje na pierwszą ćwiartkę płaszczyzny a = 0
VIII	0	1	1	-1	ZA		szósty oktant
IX	0	1	1	1	ZA	ma hipersferę jako szczególny przypadek	drugi oktant

Rysunek 1. Przestrzeń parametrów jako 3-płaszczyznowa (klasa A) i ortogonalna pół 3-płaszczyznowa (klasa B) w R ⁴ o współrzędnych ( n ⁽¹⁾ , n ⁽²⁾ , n ⁽³⁾ , a ), ukazujący kanonicznych przedstawicieli każdego typu Bianchi.

Standardową klasyfikację Bianchi można wyprowadzić ze stałych strukturalnych w następujących sześciu krokach:

1. Ze względu na antysymetrię istnieje dziewięć niezależnych stałych . Mogą być one równoważnie reprezentowane przez dziewięć składowych dowolnej stałej macierzy C ^ab : gdzie ε _abd jest całkowicie antysymetrycznym trójwymiarowym symbolem Levi-Civity (ε ₁₂₃ = 1). Zmiana tego wyrażenia dla karne tożsamości Jacobiego , skutkuje${\ Displaystyle C_ {ab} ^ {c} = - C_ {ba} ^ {c}}$${\ Displaystyle C_ {ab} ^ {c}}$
   ${\ Displaystyle C_ {ab} ^ {c} = \ varepsilon _ {abd} C ^ {DC}}$
   ${\ Displaystyle C_ {ab} ^ {c}}$
   ${\ Displaystyle \ varepsilon _ {abd} C ^ {bd} C ^ {ac} = 0.}$
2. Stałe struktury można przekształcić jako: Pojawienie się det A w tym wzorze wynika z faktu, że symbol ε _abd przekształca się jako gęstość tensora: , gdzie έ _mnd ≡ ε _mnd . Dzięki tej transformacji zawsze można zredukować macierz C ^ab do postaci: Po takim wyborze nadal mamy swobodę dokonywania transformacji triady, ale z ograniczeniami i
   ${\ Displaystyle C ^ {ab} = \ lewo (\ det {A} \ prawej) ^ {- 1} A_ {m} ^ {a} A_ {n} ^ {b} {\ ostra {C}} ^ { m.}.}$
   ${\ Displaystyle \ varepsilon _ {abc} = \ lewo (\ det {A} \ prawo) D_ {a} ^ {m} D_ {b} ^ {n} D_ {c} ^ {d} {\ ostry {\ varepsilon }}_{mnd}}$
   ${\ Displaystyle C ^ {ab} = {\ zacząć {bmatrix} n_ {1} i 0 i 0 \ \ 0 i C ^ {22} i C ^ {23} \ \ 0 i C ^ {32} i C ^ {33} \ koniec {bmatrix}} .}$
   ${\displaystyle A_{2}^{1}=A_{3}^{1}=0}$${\displaystyle A_{1}^{2}=A_{1}^{3}=0.}$
3. Teraz tożsamości Jacobi dają tylko jedno ograniczenie:
   ${\ Displaystyle \ lewo (C ^ {23} - C ^ {32} \ prawej) n_ {1} = 0.}$
4. Jeżeli n ₁ ≠ 0 to C ²³ – C ³² = 0 i przez pozostałe przekształcenia z , macierz 2 × 2 w C ^ab może być przekątna. Wtedy warunek przekątności dla C ^ab jest zachowany przy przekształceniach diagonalnych . W ramach tych przekształceń trzy parametry n ₁ , n ₂ , n ₃ zmieniają się w następujący sposób: Dzięki tym przekształceniom diagonalnym moduł dowolnego n _a (jeśli nie jest równy zero) może być równy jedności. Biorąc pod uwagę, że jednoczesna zmiana znaku wszystkich n _a nie daje nic nowego, dochodzimy do następujących niezmiennie różnych zbiorów dla liczb n ₁ , n ₂ , n ₃ (niezmiennie różnych w tym sensie, że nie ma możliwości przejścia od jeden do drugiego przez pewną transformację triady ), czyli do następujących różnych typów przestrzeni jednorodnych o macierzy diagonalnej C ^ab :${\ Displaystyle A_ {\ bar {b}} ^ {\ bar {a}} \ neq 0, \ quad {\ bar {a}}, {\ bar {b}} = {\ bar {2}}, { \bar {3}}}$${\ Displaystyle C ^ {{\ bar {a}} {\ bar {b}}}}$
   ${\ Displaystyle C ^ {ab} = {\ zacząć {bmatrix} n_ {1} i 0 i 0 \ \ 0 i n {2} i 0 \ \ 0 i 0 i n_ {3} \ koniec {bmatrix}}.}$
   ${\ Displaystyle A_ {b} ^ {a}}$
   ${\ Displaystyle n_ {a} = \ po lewej (A_ {1} ^ {1} A_ {2} ^ {2} A_ ^ {3} \ po prawej) \ po lewej (A_ {a} ^ {a} \ po prawej)^{2}{\ostre {n}}_{a},{\text{bez sumowania}}\ a.}$
   ${\ Displaystyle e_ {a} ^ {\ bar {a}} = A_ {\ bar {b}} ^ {\ bar {a}} e_ {a} ^ {\ bar {b}}}$
   ${\ Displaystyle {\ zacząć {macierz} Bianchi\ IX i: i (n_ {1}, n_ {2}, n_ {3}) i = i (1,1,1), \\ Bianchi\ VIII i: i (n_ {1},n_{2},n_{3})&=&(1,1,-1),\\Bianchi\ VII_{0}&:&(n_{1},n_{2},n_{ 3})&=&(1,1,0),\\Bianchi\ VI_{0}&:&(n_{1},n_{2},n_{3})&=&(1,-1, 0),\\Bianchi\ II&:&(n_{1},n_{2},n_{3})&=&(1,0,0).\end{macierz}}}$
5. Rozważmy teraz przypadek n ₁ = 0. Może się również zdarzyć w tym przypadku, że C ²³ – C ³² = 0. Powraca to do sytuacji już analizowanej w poprzednim kroku, ale z dodatkowym warunkiem n ₁ = 0. Teraz zasadniczo wszystko różne typy zestawów n ₁ , n ₂ , n ₃ to (0, 1, 1), (0, 1, −1), (0, 0, 1) i (0, 0, 0). Pierwsze trzy powtarzają typy VII ₀ , VI ₀ , II . W konsekwencji powstaje tylko jeden nowy typ:
   ${\displaystyle Bianchi\ ja\ :\ (n_{1},n_{2},n_{3})\ =\ (0,0,0).}$
6. Jedyny pozostały przypadek to n ₁ = 0 i C ²³ – C ³² ≠ 0. Teraz macierz 2 × 2 jest niesymetryczna i nie można jej zrobić diagonalnie za pomocą przekształceń . Jednak jej symetryczna część może być przekątna, czyli macierz 3×3 C ^ab może być sprowadzona do postaci: gdzie a jest dowolną liczbą. Po wykonaniu tej operacji, nadal istnieje możliwość dokonania przemiany o przekątnej , zgodnie z którym ilość N ₂ , N ₃ i zmieniają się w następujący sposób: preparaty te pokazują, że dla niezerowego n- ₂ , n- ₃ , a , połączenie ² ( n ₂ n ₃ ) ⁻¹ jest wielkością niezmienną. Wybierając , można narzucić warunek a > 0 i po wykonaniu tego wybór znaku pozwala na zmianę obu znaków n ₂ i n ₃ jednocześnie, czyli zbioru ( n ₂ , n ₃ ) jest równoważne zbiorem (- n ₂ , - n ₃ ). Wynika z tego, że istnieją następujące cztery różne możliwości: W przypadku dwóch pierwszych liczba a może zostać przekształcona w jedność poprzez wybór parametrów i . W przypadku dwóch drugich możliwości oba te parametry są już ustalone, a a pozostaje niezmienną i dowolną liczbą dodatnią. Historycznie te cztery typy przestrzeni jednorodnych zostały sklasyfikowane jako: Typ III jest tylko szczególnym przypadkiem typu VI odpowiadającego a = 1. Typy VII i VI zawierają nieskończoność niezmiennie różnych typów algebr odpowiadających arbitralności parametru ciągłego a . Typ VII ₀ jest szczególnym przypadkiem VII odpowiadającym a = 0, podczas gdy typ VI ₀ jest szczególnym przypadkiem VI odpowiadającym również a = 0.${\ Displaystyle C ^ {{\ bar {a}} {\ bar {b}}} ({\ bar {a}}, {\ bar {b}} = 2,3)}$${\ Displaystyle A_ {\ bar {b}} ^ {\ bar {a}} \ neq 0}$
   ${\ Displaystyle C ^ {ab} = {\ zacznij {bmatrix} 0 i 0 i 0 \ \ 0 i n_ {2} i a \ \ 0 i - a i n_ {3} \ koniec {bmatrix}}}$
   ${\ Displaystyle A_ {\ bar {b}} ^ {\ bar {a}}}$
   ${\ Displaystyle n_ {2} = \ po lewej (A_ {1} ^ {1} A_ {2} ^ {2} A_ ^ {3} \ po prawej) ^ {-1} \ po lewej (A_ {2} ^{2}\right)^{2}{\acute {n}}_{2},\quad n_{3}=\left(A_{1}^{1}A_{2}^{2}A_ {3}^{3}\right)^{-1}\left(A_{3}^{3}\right)^{2}{\acute {n}}_{3},\quad a=\ lewa(A_{1}^{1}\prawa)^{-1}{\ostra {a}}.}$
   ${\displaystyle A_{1}^{1}}$${\ Displaystyle A_ {3} ^ {3} \ lewo (A_ {2} ^ {2} \ prawy) ^ {-1}}$
   ${\displaystyle (a,n_{2},n_{3})=(a,0,0),(a,0,1),(a,1,1),(a,1,-1). }$
   
   ${\displaystyle A_{1}^{1}}$${\ Displaystyle A_ {3} ^ {3} \ lewo (A_ {2} ^ {2} \ prawy) ^ {-1}}$
   ${\ Displaystyle {\ zacząć {macierz} Bianchi\ V&:&n_{1}=0,\(a,n_{2},n_{3})&=&(1,0,0),\\Bianchi\ IV& :&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,0,1),\\Bianchi\ VII&:&n_{1}=0,\ (a, n_ {2}, n_ {3}) & = & (a, 1,1), \\ Bianchi \ III &: & n_ {1} = 0, \ (a, n_ {2}, n_ {3}) & = &(1,1,-1),\\Bianchi\ VI&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(a,1,-1).\ koniec{matryca}}}$
   

Krzywizna przestrzeni Bianchi

Przestrzenie Bianchiego mają tę właściwość, że ich tensory Ricciego można rozdzielić na iloczyn wektorów bazowych związanych z przestrzenią i tensora niezależnego od współrzędnych.

Dla danej metryki :

${\ Displaystyle ds ^ {2} = \ gamma _ {ab} \ xi _ {i} ^ {(a)} \ xi _ {k} ^ {(b)} dx ^ {i} dx ^ {k}}$

(gdzie 　są 1-formy ), tensor krzywizny Ricciego jest określony wzorem : ${\ Displaystyle \ xi _ {i} ^ {(a)} dx ^ {i}}$${\ Displaystyle R_ {ik}}$

${\ Displaystyle R_ {ik} = R_ {(a) (b)} \ xi _ {i} ^ {(a)} \ x _ {k} ^ {(b)}}$

${\ Displaystyle R_ {(a) (b)} = {\ Frac {1} {2}} \ lewo [C_ {\ \ b} ^ {cd} \ lewo (C_ {cda} + C_ {dca} \ prawej) )+C_{\ cd}^{c}\left(C_{ab}^{\ \ d}+C_{ba}^{\ \ d}\right)-{\frac {1}{2}}C_ {b}^{\ cd}C_{acd}\right]}$

gdzie indeksy na stałych struktury są podnoszone i obniżane z których nie jest funkcją . ${\ Displaystyle \ gamma _ {ab}}$${\ Displaystyle x ^ {i}}$

Zastosowanie kosmologiczne

W kosmologii ta klasyfikacja jest stosowana dla jednorodnej czasoprzestrzeni o wymiarze 3+1. Trójwymiarowa grupa Liego jest grupą symetrii trójwymiarowego, przestrzennego wycinka, a metryka Lorentza spełniająca równanie Einsteina jest generowana przez zmianę składowych metrycznych w funkcji t. Te dane Friedmann-Lemaître-Robertson-Walker są izotropowe, które są szczególnymi przypadkami typu I, V, i IX. Modele Bianchi typu I zawierają metrykę Kasner jako przypadek szczególny. Kosmologie Bianchi IX zawierają metrykę Tauba . Jednak dynamiką w pobliżu osobliwości w przybliżeniu rządzi seria kolejnych okresów Kasnera (Bianchi I). Skomplikowana dynamika, która zasadniczo sprowadza się do ruchu bilardowego w części przestrzeni hiperbolicznej, wykazuje chaotyczne zachowanie i nosi nazwę Mixmaster ; jego analiza jest określana jako analiza BKL po Bielińskim, Khalatnikovie i Lifshitzu. W nowszych pracach ustalono związek teorii (super-)grawitacji w pobliżu przestrzennej osobliwości (granica BKL) z algebrami Lorentza Kaca-Moody'ego , grupami Weyla i hiperbolicznymi grupami Coxetera . Inne, nowsze prace dotyczą dyskretnej natury mapy Kasnera i ciągłego uogólniania. W przestrzeni, która jest zarówno jednorodna, jak i izotropowa, metryka jest określana całkowicie, pozostawiając wolny tylko znak krzywizny. Założenie tylko jednorodności przestrzeni bez dodatkowej symetrii, takiej jak izotropia, daje znacznie większą swobodę w doborze metryki. Poniższe odnosi się do przestrzennej części metryki w danej chwili t, przy założeniu synchronicznej klatki, tak że t jest tym samym zsynchronizowanym czasem dla całej przestrzeni. ${\ Displaystyle \ scriptstyle {\ tekst {VII}} _ {h}}$

Jednorodność oznacza identyczne właściwości metryczne we wszystkich punktach przestrzeni. Dokładna definicja tego pojęcia obejmuje rozważenie zestawów przekształceń współrzędnych, które przekształcają przestrzeń w siebie, tj. Pozostawiają niezmienioną metrykę: jeśli element liniowy przed transformacją jest

${\ Displaystyle dl ^ {2} = \ gamma _ {\ alfa \ beta} \ lewo (x ^ {1}, x ^ {2}, x ^ {3} \ prawej) dx ^ {\ alfa} dx ^ { \beta},}$

to po transformacji ten sam element liniowy jest

${\ Displaystyle dl ^ {2} = \ gamma _ {\ alfa \ beta} \ lewo (x ^ {\ pierwsza}, x ^ {\ pierwsza 2}, x ^ {\ pierwsza 3} \ prawej) dx ^ { \ prime \ alpha} dx ^ {\ prime \ beta},}$

z tą samą funkcjonalną zależnością γ _αβ od nowych współrzędnych. (Aby uzyskać bardziej teoretyczną i niezależną od współrzędnych definicję przestrzeni jednorodnej, zobacz jednorodną przestrzeń ). Przestrzeń jest jednorodna, jeśli dopuszcza zbiór przekształceń ( grupy ruchów ), które sprowadzają dowolny punkt do położenia dowolnego innego punktu. Ponieważ przestrzeń jest trójwymiarowa, różne przekształcenia grupy są oznaczone trzema niezależnymi parametrami.

Rysunek 2. Triada e ^{( a )} ( e ⁽¹⁾ , e ⁽²⁾ , e ⁽³⁾ ) jest afinicznym układem współrzędnych (w tym w szczególnym przypadku kartezjańskim układem współrzędnych), którego współrzędne są funkcjami współrzędnych krzywoliniowych x _α (x ₁ , x ₂ , x ₃ ).

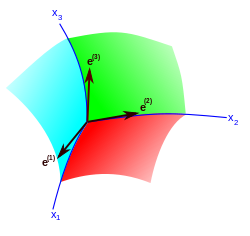
W przestrzeni euklidesowej jednorodność przestrzeni wyraża się niezmiennością metryki przy równoległych przemieszczeniach ( translacjach ) kartezjańskiego układu współrzędnych . Każde przesunięcie jest określone przez trzy parametry — składowe wektora przemieszczenia początku współrzędnych. Wszystkie te przekształcenia pozostawiają niezmienne trzy niezależne różniczki ( dx , dy , dz ), z których skonstruowany jest element liniowy. W ogólnym przypadku nieeuklidesowej przestrzeni jednorodnej przekształcenia jej grupy ruchów ponownie pozostawiają niezmienne trzy niezależne liniowe formy różniczkowe , które nie sprowadzają się jednak do różniczek całkowitych żadnych funkcji współrzędnych. Formy te są zapisywane w taki sposób, w którym indeks łaciński ( a ) oznacza trzy niezależne wektory (funkcje współrzędnych); wektory te nazywane są polem ramki lub triadą. Greckie litery oznaczają trzy przestrzenne współrzędne krzywoliniowe . Niezmiennik metryki przestrzennej konstruuje się pod zadaną grupą ruchów za pomocą powyższych form: ${\ Displaystyle e_ {\ alfa} ^ {(a)} dx ^ {\ alfa}}$

${\ Displaystyle dl ^ {2} = \ eta _ {ab} \ lewo (e _ {\ alpha} ^ {(a)} dx ^ {\ alfa} \ prawo) \ lewo (e _ {\ beta} ^ {(b )}dx^{\beta }\right)}$

( równanie 6a )

tj. tensor metryczny to

${\ Displaystyle \ gamma _ {\ alfa \ beta} = \ eta _ {ab} e_ {\ alfa} ^ {(a)} e_ {\ beta} ^ {(b)}}$

( równanie 6b )

gdzie współczynniki η _ab , które są symetryczne we wskaźnikach a i b , są funkcjami czasu. Wybór wektorów bazowych jest podyktowany własnościami symetrii przestrzeni i na ogół te wektory bazowe nie są ortogonalne (tak, że macierz η _ab nie jest diagonalna).

Odwrotna trójka wektorów jest wprowadzana za pomocą delta Kroneckera${\ Displaystyle e_ {(a)} ^ {\ alfa}}$

${\ Displaystyle e_ {(a)} ^ {\ alfa} e_ {\ alfa} ^ {(b)} = \ delta _ {a} ^ {b}; \ quad e_ {(a)} ^ {\ alfa} e _ {\ beta} ^ {(a)} = \ delta _ {\ alpha} ^ {\ beta}}$

( równanie 6c )

W przypadku trójwymiarowym związek między dwiema trójkami wektorowymi można zapisać w sposób jawny

${\ Displaystyle \ mathbf {e} _ {(1)} = {\ Frac {1} {v}} \ mathbf {e} ^ {(2)} \ razy \ mathbf {e} ^ {(3)}, \quad \mathbf {e} _{(2)}={\frac {1}{v}}\mathbf {e} ^{(3)}\times \mathbf {e} ^{(1)},\ quad \ mathbf {e} _ {(3)} = {\ frac {1} {v}} \ mathbf {e} ^ {(1)} \ times \ mathbf {e} ^ {(2)},}$

( równ. 6d )

gdzie objętość v jest

${\ Displaystyle V = \ lewo \ vert e_ {\ alfa} ^ {(a)} \ prawej \ vert = \ mathbf {e} ^ {(1)} \ cdot \ mathbf {e} ^ {(2)} \ razy \mathbf {e} ^{(3)},}$

gdzie e _{( a )} i e ^{( a )} uważane są za wektory kartezjańskie ze składowymi i odpowiednio . Wyznacznikiem tego tensora metrycznego eq. 6b to γ = η v ² gdzie η jest wyznacznikiem macierzy η _ab . ${\ Displaystyle e_ {(a)} ^ {\ alfa}}$${\ Displaystyle e_ {\ alfa} ^ {(a)}}$

Wymagane warunki jednorodności przestrzeni to

${\ Displaystyle \ lewo ({\ Frac {\ częściowy e_ {\ alfa} ^ {(c)}} {\ częściowy x ^ {\ beta}}} - {\ Frac {\ częściowy e_ {\ beta} ^ {( c)}}{\partial x^{\alpha }}}\right)e_{(a)}^{\alpha }e_{(b)}^{\beta }=C_{ab}^{c}. }$

( równ. 6e )

Stałe nazywane są stałymi strukturalnymi grupy. ${\ Displaystyle C_ {ab} ^ {c}}$

Dowód równ. 6e

Niezmienność form różniczkowych oznacza, że: ${\ Displaystyle e_ {\ alfa} ^ {(a)} dx ^ {\ alfa}}$ ${\ Displaystyle e_ {\ alfa} ^ {(a)} (x) dx ^ {\ alfa} = e_ {\ alfa} ^ {(a)} (x ^ {\ prime}) dx ^ {\ prime \ alfa }}$ gdzie po obu stronach równania są te same funkcje, odpowiednio, starych i nowych współrzędnych. Mnożąc to równanie przez , ustalając i porównując współczynniki tych samych różniczek dx α , otrzymujemy${\ Displaystyle e_ {\ alfa} ^ {(a)}}$${\ Displaystyle e_ {(a)} ^ {\ beta} (x ^ {\ prime})}$${\ Displaystyle dx ^ {\ prime \ beta} = {\ Frac {\ częściowe x ^ {\ prime \ beta}} {\ częściowe x ^ {\ alfa}}} dx ^ {\ alfa},}$ ${\ Displaystyle {\ Frac {\ częściowy x ^ {\ prime \ beta}} {\ częściowy x ^ {\ alfa}}} = e_ {(a)} ^ {\ beta} (x ^ {\ prime}) e_ {\alfa }^{(a)}(x).}$ Równania te są układem równań różniczkowych, które określają funkcje dla danego układu. Aby być całkowalnym, równania te muszą spełniać identycznie warunki ${\ Displaystyle x ^ {\ prime \ beta} (x)}$ ${\ Displaystyle {\ Frac {\ częściowy ^ {2} x ^ {\ prime \ beta}} {\ częściowy x ^ {\ alfa} \ częściowy x ^ {\ gamma}}} = {\ Frac {\ częściowy ^ { 2}x^{\prime \beta }}{\partial x^{\gamma }\partial x^{\alpha }}}.}$ Obliczając pochodne, stwierdza się ${\ Displaystyle \ lewo [{\ Frac {\ częściowy e_ {(a)} ^ {\ beta} (x ^ {\ prime})} {\ częściowy x ^ {\ prime \ delta}}} e_ {(b) }^{\delta }(x^{\prime })-{\frac {\partial e_{(b)}^{\beta }(x^{\prime })}{\partial x^{\prime \ delta }}}e_{(a)}^{\delta }(x^{\prime })\right]e_{\gamma }^{(b)}(x)e_{\alpha }^{(a) }(x)=e_{(a)}^{\beta }(x^{\prime })\left[{\frac {\częściowy e_{\gamma }^{(a)}(x)}{\ częściowe x ^ {\ alpha}}} - {\ frac {\ częściowe e _ {\ alpha} ^ {(a)} (x)} {\ częściowe x ^ {\ gamma}}} \ right].}$ Mnożąc obie strony równań przez i przesuwając zróżnicowanie z jednego czynnika na drugi za pomocą równ. 6c , dostaje się za lewą stronę: ${\ Displaystyle e_ {(d)} ^ {\ alfa} (x) e_ {(c)} ^ {\ gamma} (x) e_ {\ beta} ^ {(f)} (x ^ {\ prime}) }$ ${\ Displaystyle e_ {\ beta} ^ {(f)} (x ^ {\ prime}) \ lewo [{\ Frac {\ częściowy e_ {(d)} ^ {\ beta} (x ^ {\ prime}) } {\ częściowy x ^ {\ prime \ delta}}} e _ {(c)} ^ {\ delta} (x ^ {\ prime}) - {\ frac {\ częściowy e _ {(c)} ^ {\ beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(d)}^{\delta }(x^{\prime })\right]=e_{(c )}^{\beta }(x^{\prime })e_{(d)}^{\delta }(x^{\prime })\left[{\frac {\częściowy e_{\beta }^{ (f)}(x^{\prime })}{\partial x^{\prime \delta }}}-{\frac {\partial e_{\delta }^{(f)}(x^{\prime })}{\częściowy x^{\prime \beta }}}\right].}$ a po prawej to samo wyrażenie w zmiennej x . Ponieważ x i x' są dowolne, to wyrażenie musi zredukować się do stałych, aby otrzymać równ. 6e .

Mnożenie przez , równ. 6e można przepisać w formie ${\ Displaystyle e_ {(c)} ^ {\ gamma}}$

${\ Displaystyle e_ {(a)} ^ {\ alfa} {\ Frac {\ częściowy e_ {(b)} ^ {\ gamma}} {\ częściowy x ^ {\ alfa}}}-e_ {(b)} ^{\beta }{\frac {\częściowy e_{(a)}^{\gamma }}{\częściowy x^{\beta }}}=C_{ab}^{c}e_{(c)}^ {\gamma}.}$

( równ. 6f )

Równanie 6e można zapisać w postaci wektorowej jako

${\ Displaystyle \ mathbf {e} _ {(a)} \ razy \ mathbf {e} _ {(b)} {\ tekst {curl}} \ mathbf {e} ^ {(c)} = - C_ {AB }^{c},}$

gdzie znowu operacje wektorowe są wykonywane tak, jakby współrzędne x ^α były kartezjańskie. Za pomocą równ. 6d , otrzymuje się

${\ Displaystyle {\ Frac {1} {v}} \ lewo (\ mathbf {e} ^ {(1)} {\ tekst {curl}} \ mathbf {e} ^ {(1)} \ prawej) = C_ {32}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(2)}{\text{curl }}\mathbf {e} ^{(1 )}\right)=C_{13}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(3)}{\text{curl }}\mathbf {e} ^{(1)}\right)=C_{21}^{1}}$

(np . 6g )

i sześć innych równań otrzymanych przez cykliczną permutację indeksów 1, 2, 3.

Stałe struktury są antysymetryczne w swoich dolnych indeksach, jak widać z ich definicji równ. 6e : . Inny warunek na stałych strukturalnych można uzyskać, zauważając, że równ. 6f można zapisać w postaci relacji komutacyjnych${\ Displaystyle C_ {ab} ^ {c} = - C_ {ba} ^ {c}}$

${\ Displaystyle \ lewo [X_ {a}, X_ {b} \ prawo] \ Equiv X_ {a} X_ {b}-X_ {b} X_ {a} = C_ {ab} ^ {c} X_ {c} }$

( równ. 6 godz. )

dla liniowych operatorów różniczkowych

${\ Displaystyle X_ {a} = e_ {(a)} ^ {\ alfa} {\ Frac {\ częściowy} {\ częściowy x ^ {\ alfa}}}}$

( równ. 6i )

Matematycznym teorii grup ciągłych ( grupy Lie ) podmiot X _A spełniający warunki eq. 6h nazywane są generatorami grupy . Teoria grup Liego wykorzystuje operatory zdefiniowane za pomocą wektorów zabijania zamiast triad . Ponieważ w metryce synchronicznej żadna ze składowych γ _{αβ nie} zależy od czasu, wektory zabijania (triady) są podobne do czasu. ${\ Displaystyle \ xi _ {(a)} ^ {\ alfa}}$${\ Displaystyle e_ {(a)} ^ {\ alfa}}$

Warunki równ. 6h podążać za tożsamością Jacobiego

${\ Displaystyle [[X_ {a}, X_ {b}], X_ {c}] + [[X_ {b}, X_ {c}], X_ {a}] + [[X_ {c}, X_ { a}],X_{b}]=0}$

i mieć formę

${\ displaystyle C_ {ab} ^ {e} C_ {ec} ^ {d} + C_ {bc} ^ {e} C_ {ea} ^ {d} + C_ {ca} ^ {e} C_ {eb} ^ {d}=0}$

( równ. 6j )

Zdecydowaną zaletą jest zastosowanie w miejsce stałych trójwskaźnikowych zbioru wielkości dwuwskaźnikowych, otrzymanych w wyniku przekształcenia podwójnego ${\ Displaystyle C_ {ab} ^ {c}}$

${\ Displaystyle C_ {ab} ^ {c} = e_ {abd} C ^ {DC}}$

( równ. 6k )

gdzie e _abc = e ^abc jest jednostkowym symbolem antysymetrycznym (gdzie e ₁₂₃ = +1). Z tymi stałymi relacje komutacji równ. 6h są napisane jako

${\ Displaystyle e ^ {abc} X_ {b} X_ {c} = C ^ {reklama} X_ {d}}$

( np . 6l )

Własność antysymetrii jest już uwzględniona w definicji równ. 6K , a własności równ. 6j przyjmuje formę

${\ Displaystyle e_ {bcd} C ^ {cd} C ^ {ba} = 0}$

(np . 6m )

Wybór trzech wektorów ramowych w formach różniczkowych (a wraz z nimi operatorów X _a ) nie jest wyjątkowy. Można je poddać dowolnej transformacji liniowej o stałych współczynnikach: ${\ Displaystyle e_ {\ alfa} ^ {(a)} dx ^ {\ alfa}}$

${\ Displaystyle \ mathbf {e} _ {(a)} = A_ {a} ^ {b} \ mathbf {e} _ {(b)}.}$

( równ. 6n )

Wielkości η _ab i C ^ab zachowują się jak tensory (są niezmienne) w odniesieniu do takich przekształceń.

Warunki równ. 6m to jedyne, które muszą spełniać stałe konstrukcji. Ale wśród stałych dopuszczalnych przez te warunki istnieją zbiory równoważne, w tym sensie, że ich różnica jest związana z przekształceniem typu równ. 6n . Zagadnienie klasyfikacji przestrzeni jednorodnych sprowadza się do wyznaczenia wszystkich nierównoważnych zbiorów stałych strukturalnych. Można to zrobić, wykorzystując właściwości „tensorowe” wielkości C ^ab , za pomocą następującej prostej metody (CG Behr, 1962).

Asymetryczny tensor C ^ab można rozdzielić na część symetryczną i antysymetryczną. Pierwszy jest oznaczony przez n ^ab , a drugi jest wyrażony jako jego podwójny wektor a _c :

${\ Displaystyle C ^ {ab} = n ^ {ab} + e ^ {abc} a_ {c}.}$

( równ. 6o )

Podstawienie tego wyrażenia w równ. 6m prowadzi do stanu

${\ Displaystyle n ^ {ab} a_ {b} = 0.}$

( np . 6p )

Za pomocą przekształceń równ. 6n symetryczny tensor n ^ab można sprowadzić do postaci diagonalnej z wartościami własnymi n ₁ , n ₂ , n ₃ . Z równania 6p wynika, że ​​wektor a _b (jeśli istnieje) leży wzdłuż jednego z głównych kierunków tensora n ^ab , odpowiadającego wartości własnej zero. Bez utraty ogólności można zatem ustawić a _b = ( a , 0, 0). Następnie równ. 6p redukuje się do a ₁ = 0, tzn. jedna z wielkości a lub n ₁ musi wynosić zero. Tożsamości Jacobiego przyjmują postać:

${\ Displaystyle [X_ {1}, X_ {2}] = - aX_ {2} + n_ {3} X_ {3}, \ quad [X_ {2}, X_ {3}] = n_ {1} X_ { 1},\quad [X_{3},X_{1}]=n_{2}X_{2}+aX_{3}.}$

( równ. 6q )

Jedyne pozostałe wolności są zmiany Znak operatorów x i ich mnożenie przez arbitralnych stałych. Pozwala to na jednoczesne zmienić znak wszystkich n _A , a także, aby liczba sztuk jest dodatni (jeśli jest różny od zera). Również wszystkie stałe struktury mogą być równe ±1, jeśli przynajmniej jedna z wielkości a , n ₂ , n ₃ zniknie. Ale jeśli wszystkie trzy z tych wielkości różnią się od zera, przekształcenia skali pozostawiają niezmienną proporcję h = a ² ( n ₂ n ₃ ) ⁻¹ .

W ten sposób dochodzi się do klasyfikacji Bianchiego wymieniającej możliwe typy przestrzeni jednorodnych sklasyfikowanych wartościami a , n ₁ , n ₂ , n _{3 ,} co graficznie przedstawiono na rys. 3. W przypadku klasy A ( a = 0) typ IX ( n ⁽¹⁾ = 1, n ⁽²⁾ = 1, n ⁽³⁾ = 1) jest reprezentowane przez oktant 2, typ VIII ( n ⁽¹⁾ = 1, n ⁽²⁾ = 1, n ⁽³⁾ =–1) jest reprezentowany przez oktant 6, podczas gdy typ VII ₀ ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =0) jest reprezentowany przez pierwszą ćwiartkę płaszczyzny poziomej i typ VI ₀ ( n ⁽¹⁾ =1, n ⁽²⁾ =–1, n ⁽³⁾ =0) jest reprezentowane przez czwartą ćwiartkę tej płaszczyzny; typ II (( n ⁽¹⁾ =1, n ⁽²⁾ =0, n ⁽³⁾ =0) jest reprezentowany przez przedział [0,1] wzdłuż n ⁽¹⁾ i typ I ( n ⁽¹⁾ =0 , n ⁽²⁾ =0, n ⁽³⁾ =0) jest na początku Podobnie w przypadku klasy B (z n ⁽³⁾ = 0), Bianchi typu VI _h ( a = h , n ⁽¹⁾ = 1, n ⁽²⁾ =–1) rzutuje na czwartą ćwiartkę płaszczyzny poziomej, a typ VII _h ( a = h , n ⁽¹⁾ =1, n ⁽²⁾ =1) rzutuje na pierwszą ćwiartkę płaszczyzny poziomej płaszczyzny; te dwa ostatnie typy to pojedyncza klasa izomorfizmu odpowiadająca powierzchni o stałej wartości funkcji h = a ² ( n ⁽¹⁾ n ⁽²⁾ ) ^-1 . Typowa taka powierzchnia jest zilustrowana w jednym oktancie, kąt θ dane przez tan  θ = | h /2| ^1/2 ; te w pozostałych oktantach są otrzymywane przez obrót o wielokrotności π /2, h naprzemiennie ze znakiem dla danej wielkości | h |. Typ III jest podtypem VI _h gdzie a = 1. Typ V ( a = 1, n ⁽¹⁾ = 0, n ⁽²⁾ = 0) to przedział (0,1] wzdłuż osi a i typ IV ( a = 1, n ⁽¹⁾ =1, n ⁽²⁾ =0) jest pionową otwartą ścianą między pierwszą a czwartą ćwiartką płaszczyzna a = 0, przy czym ta ostatnia daje granicę klasy A dla każdego typu.

Równania Einsteina dla wszechświata o jednorodnej przestrzeni można zredukować do układu równań różniczkowych zwyczajnych zawierających tylko funkcje czasu za pomocą pola ramki. W tym celu należy rozłożyć składowe przestrzenne czterech wektorów i czterech tensorów wzdłuż triady wektorów bazowych przestrzeni:

${\ Displaystyle R_ {(a) (b)} = R_ {\ alfa \ beta} e_ {(a)} ^ {\ alfa} e_ {(b)} ^ {\ beta}, \ quad R_ {0 (a )}=R_{0\alpha }e_{(a)}^{\alpha },\quad u^{(a)}=u^{\alpha }e_{\alpha }^{(a)},}$

gdzie wszystkie te wielkości są teraz funkcjami samego t ; wielkości skalarne, gęstość energii ε i ciśnienie materii p są również funkcjami czasu.

Równania Einsteina w próżni w synchronicznym układzie odniesienia to

${\ Displaystyle R_ {0} ^ {0} = - {\ Frac {1} {2}} {\ Frac {\ części \ varkappa _ {\ alpha} ^ {\ alpha}} {\ częściowe t}} - { \frac {1}{4}}\varkappa _{\alpha }^{\beta }\varkappa _{\beta }^{\alpha }=0,}$

( równ. 11 )

${\ Displaystyle R_ {\ alfa} ^ {\ beta} = - {\ Frac {1} {2 {\ sqrt {-g}}}} {\ Frac {\ częściowy} {\ częściowy t}} \ lewo ({{ \sqrt {-g}}\varkappa _{\alpha }^{\beta }\right)-P_{\alpha }^{\beta }=0,}$

( równ. 12 )

${\ Displaystyle R_ {\ alfa} ^ {0} = {\ Frac {1} {2}} \ lewo (\ varkappa _ {\ alfa; \ beta} ^ {\ beta} - \ varkappa _ {\ beta; \ alpha} ^ {\ beta} \ right) = 0,}$

( równ. 13 )

gdzie jest trójwymiarowym tensorem , a P _αβ jest trójwymiarowym tensorem Ricciego , który jest wyrażany przez trójwymiarowy tensor metryczny γ _αβ w taki sam sposób, jak R _ik jest wyrażany przez g _ik ; P _αβ zawiera tylko pochodne przestrzenne (ale nie czasowe) γ _αβ . Używając triad, dla równ. 11 jeden ma po prostu ${\ displaystyle \ varkappa _ {\ alpha} ^ {\ beta}}$${\ Displaystyle \ varkappa _ {\ alfa} ^ {\ beta} = {\ Frac {\ częściowy \ gamma _ {\ alfa} ^ {\ beta}} {\ częściowy t}}}$

${\ Displaystyle \ varkappa _ {(a) (b)} = {\ Frac {\ częściowe \ eta _ {ab}} {\ częściowe t}}, \ quad \ varkappa _ {(a)} ^ {(b) }={\frac {\częściowy \eta _{ac}}{\częściowy t}}\eta ^{cb}.}$

Składowe P _{( a ) ( b )} można wyrazić w kategoriach wielkości η _ab i stałych strukturalnych grupy za pomocą tetradowej reprezentacji tensora Ricciego w kategoriach wielkości${\ Displaystyle \ lambda _ {abc} = \ lewo (e_ {(a) i, k} -e_ {(a) k, i} \ prawej) e_ {(b)} ^ {i} e_ {(c) }^{k}}$

${\ Displaystyle R_ {(a) (b)} = - {\ Frac {1} {2}} \ lewo (\ lambda _ {ab, c} ^ {c} + \ lambda _ {ba, c} ^ { c}+\lambda _{ca,b}^{c}+\lambda _{cb,a}^{c}+\lambda _{b}^{cd}\lambda _{cda}+\lambda _{ b}^{cd}\lambda _{dca}-{\frac {1}{2}}\lambda _{b}^{cd}\lambda _{acd}+\lambda _{cd}^{c} \lambda _{ab}^{d}+\lambda _{cd}^{c}\lambda _{ba}^{d}\right).}$

Po zastąpieniu symboli trójindeksowych symbolami ^{dwuindeksowymi} C ^ab i przekształceniach: ${\ displaystyle \ lambda _ {bc} ^ {a} = C_ {bc} ^ {a}}$

${\ Displaystyle \ eta _ {reklama} \ eta _ {BC} \ eta _ {cf} e ^ {def} = \ eta e_ {abc}, \ quad e_ {abf} e ^ {cdf} = \ delta _ { a}^{c}\delta _{b}^{d}-\delta _{a}^{d}\delta _{b}^{c}}$

otrzymujemy „jednorodny” tensor Ricciego wyrażony w stałych strukturalnych:

${\ Displaystyle P_ {(a)} ^ {(b)} = {\ Frac {1} {2 \ eta}} \ lewo \ {2C ^ {bd} C_ {reklama} + C ^ {db} C_ {reklama } + C ^ {bd} C_ {da} -C_ {d} ^ {d} \ left (C_ {a} ^ {b} + C_ {a} ^ {b} \ right) + \ delta _ {a} ^{b}\left[\left(C_{d}^{d}\right)^{2}-2C^{df}C_{df}\right]\right\}.}$

Tutaj wszystkie indeksy są podnoszone i obniżane za pomocą lokalnego tensora metryki η _ab

${\ Displaystyle C_ {a} ^ {b} = \ eta _ {ac} C ^ {cb} \ quad C_ {ab} = \ eta _ {ac} \ eta _ {bd} C ^ {cd}.}$

Do tożsamości Bianchi dla trójwymiarowego tensora P _αβ w jednorodnej przestrzeni przybrać formę

${\ Displaystyle P_ {b} ^ {c} C_ {ca} ^ {b} + P_ {a} ^ {c} C_ {cb} ^ {b} = 0.}$

Uwzględnienie przekształceń pochodnych kowariantnych dla dowolnych czterech wektorów A _i oraz czterech tensorów A _ik

${\ Displaystyle A_ {i; k} e_ {(a)} ^ {i} e_ {(b)} ^ {k} = A_ {(a) (b)} -A ^ {(d)} \ gamma _ {zimnica},}$

${\ Displaystyle A_ {ik; l} e_ {(a)} ^ {i} e_ {(b)} ^ {k} e_ {(c)} ^ {l} = A_ {(a) (b) (c )}-A_{(b)}^{(d)}\gamma _{dac}+A_{(a)}^{(d)}\gamma _{dbc},}$

końcowe wyrażenia dla składowych triad czterotensora Ricciego to:

${\ Displaystyle R_ {0}^ {0} = - {\ Frac {1} {2}} {\ Frac {\ częściowy \ varkappa _ {(a)} ^ {(a)}} {\ częściowy t}} -{\frac {1}{4}}\varkappa _{(a)}^{(b)}\varkappa _{(b)}^{(a)},}$

( równ. 11a )

${\ Displaystyle R_ {(a)} ^ {(b)} = - {\ Frac {1} {2 {\ sqrt {\ eta}}}} {\ Frac {\ częściowy} {\ częściowy t}} \ lewo ({\sqrt {\eta }}\varkappa _{(a)}^{(b)}\right)-P_{(a)}^{(b)},}$

( równ. 12a )

${\ Displaystyle R_ {(a)} ^ {0}= - {\ Frac {1} {2}} \ varkappa _ {(b)} ^ {(c)} \ lewo (C_ {ca} ^ {b} -\delta _{a}^{b}C_{dc}^{d}\prawo).}$

( równ. 13a )

Przy tworzeniu równań Einsteina nie ma więc potrzeby stosowania wyraźnych wyrażeń dla wektorów bazowych jako funkcji współrzędnych.

Zobacz też

• Tabela grup kłamstw
• Lista prostych grup Liego
• Osobliwość BKL

Uwagi

Bibliografia

Bibliografia