Historia trygonometrii - History of trigonometry
| Trygonometria |
|---|
 |
| Referencja |
| Prawa i twierdzenia |
| Rachunek różniczkowy |
Wczesne badania trójkątów można prześledzić do drugiego tysiąclecia pne , w matematyce egipskiej ( Papirus matematyczny Rhinda ) i matematyce babilońskiej . Trygonometria była również powszechna w matematyce kuszyckiej . Systematyczne badania funkcji trygonometrycznych rozpoczęły się w matematyce hellenistycznej , docierając do Indii jako część hellenistycznej astronomii . W astronomii indyjskiej badania funkcji trygonometrycznych rozkwitły w okresie Gupty , szczególnie za sprawą Aryabhaty (VI wiek n.e.), który odkrył funkcję sinus. W średniowieczu studiowanie trygonometrii kontynuowano w matematyce islamskiej przez takich matematyków jak Al-Khwarizmi i Abu al-Wafa . Stała się niezależną dyscypliną w świecie islamskim , gdzie znane były wszystkie sześć funkcji trygonometrycznych . Tłumaczenia tekstów arabskich i greckich doprowadziły do przyjęcia trygonometrii jako przedmiotu na łacińskim Zachodzie, począwszy od renesansu od Regiomontanus . Rozwój nowoczesnej trygonometrii przesunął się w zachodniej epoce Oświecenia , poczynając od XVII-wiecznej matematyki ( Izaak Newton i James Stirling ) aż po współczesną formę u Leonharda Eulera (1748).
Etymologia
Termin „trygonometria” pochodzi od greckiego τρίγωνον trigōnon , „trójkąt” i μέτρον metron , „miara”.
Współczesne słowo „sine” pochodzi od łacińskiego słowa sinus , co oznacza „zatoka”, „piersi” lub „fałd” jest pośrednio, poprzez transmisję indyjską, perską i arabską, wywodzące się z greckiego terminu khordḗ „struna, akord”. ”. Hinduski termin oznaczający sinus w sanskrycie to jyā „ cięciwa ”, Hindusi pierwotnie wprowadzili i zwykle stosowali trzy funkcje trygonometryczne jyā, koti-jyā i utkrama-jyā. Hindusi określali je jako funkcje łuku koła, a nie kąta, stąd ich skojarzenie z cięciwą łuku i stąd „cięciwa łuku” dla łuku nazywana jest „łukiem” (dhanu, capa). Jej synonimami są jiva, siñjini, maurvi, guna itd. Funkcja sinusa została później zaadaptowana również w wariancie jīvā . Sanskryt jīvā został przetłumaczony (przyjęty) na arabski jako jiba , pisany jb جب. Zostało to następnie zinterpretowane jako prawdziwe arabskie słowo jayb , oznaczające „piersi, fałda, zatoka”, albo przez Arabów, albo przez pomyłkę europejskich tłumaczy, takich jak Robert z Chester , który przetłumaczył jayb na łacinę jako sinus . Szczególnie Fibonacciego jest sinus rectus Arcus okazała wpływowy w ustaleniu terminu zatok . Słowa „minuta” i „druga” pochodzą od łacińskich zwrotów partes minutae primae i partes minutae secundae . Te z grubsza przekładają się na „pierwsze małe części” i „drugie małe części”.
Rozwój
Starożytny Bliski Wschód
Starożytni Egipcjanie i Babilończycy od wieków znali twierdzenia o stosunkach boków podobnych trójkątów. Ponieważ jednak społecznościom przed helleńskim brakowało koncepcji miary kąta, ograniczały się one do badania boków trójkątów.
Na babilońskich astronomów przechowywane szczegółowe zapisy na wschody i zachody gwiazdek , Ruch planet oraz Słońca i Księżyca zaćmienia , z których wszystkie wymagane znajomość kątowych odległościach mierzonych na sferze niebieskiej . Opierając się na jednej z interpretacji tabliczki klinowej Plimpton 322 (ok. 1900 pne), niektórzy twierdzili nawet, że starożytni Babilończycy mieli tablicę z sekantami. Istnieje jednak wiele dyskusji, czy jest to tablica trójek pitagorejskich , rozwiązanie równań kwadratowych, czy tablica trygonometryczna .
Z drugiej strony Egipcjanie używali prymitywnej formy trygonometrii do budowy piramid w II tysiącleciu p.n.e. Papirus Matematyczny Rhinda , napisany przez egipskiego pisarza Ahmes (c. 1680/20 pne), zawiera następujący problem związany z trygonometrii:
„Jeżeli piramida ma 250 łokci wysokości, a bok jej podstawy 360 łokci długości, to czym jest jej sekwencja ?”
Rozwiązaniem problemu Ahmesa jest stosunek połowy boku podstawy piramidy do jej wysokości, czyli stosunek rozbiegu do wzniesienia jej lica. Innymi słowy, wielkość, którą znalazł dla seked, to cotangens kąta do podstawy piramidy i jej czoła.
Klasyczny antyk
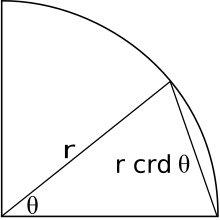
Z akordu korzystali starożytni matematycy greccy i hellenistyczni . Mając okrąg i łuk na okręgu, cięciwa jest linią leżącą pod łukiem. Dwusieczna prostopadła cięciwy przechodzi przez środek okręgu i przecina kąt na pół. Jedna połowa dwusiecznej cięciwy jest sinusem połowy dwusiecznej kąta, czyli
i w konsekwencji funkcja sinus jest również znana jako półakord . Ze względu na ten związek wiele tożsamości trygonometrycznych i twierdzeń, które są dziś znane, było również znanych hellenistycznym matematykom, ale w ich równoważnej formie akordów.
Chociaż w pracach Euklidesa i Archimedesa nie ma trygonometrii , w ścisłym tego słowa znaczeniu, istnieją twierdzenia przedstawione w sposób geometryczny (a nie trygonometryczny), które są równoważne określonym prawom lub wzorom trygonometrycznym. Na przykład, twierdzenia dwunaste i trzynaste z księgi drugiej Elementów są prawami cosinusów odpowiednio dla kątów rozwartych i ostrych. Twierdzenia o długościach cięciw to zastosowania prawa sinusów . A twierdzenie Archimedesa o łamanych akordach jest równoważne wzorom na sinusy sum i różnice kątów. Aby zrekompensować brak tabeli akordów , matematycy z czasów Arystarcha używali czasami stwierdzenia, że we współczesnej notacji sin α /sin β < α / β < tan α / tan β, gdy 0° < β < α < 90°, obecnie znane jako nierówność Arystarcha .
Pierwsza tabela trygonometryczna została najwyraźniej skompilowana przez Hipparcha z Nicei (180 – 125 pne), który jest obecnie znany jako „ojciec trygonometrii”. Hipparch był pierwszym, który zestawił odpowiednie wartości łuku i cięciwy dla szeregu kątów.
Chociaż nie wiadomo, kiedy systematyczne użycie okręgu 360° weszło do matematyki, wiadomo, że systematyczne wprowadzanie okręgu 360° nastąpiło nieco po Arystarchusie z Samos skomponowanej O rozmiarach i odległościach Słońca i Księżyca (ok. 260 pne), ponieważ zmierzył kąt jako ułamek kwadrantu. Wydaje się, że systematyczne stosowanie koła 360° jest w dużej mierze zasługą Hipparcha i jego tabeli akordów . Hipparch mógł zaczerpnąć ideę tego podziału od Hypsiclesa, który wcześniej podzielił dzień na 360 części, podział dnia sugerowany przez astronomię babilońską. W starożytnej astronomii zodiak był podzielony na dwanaście „znaków” lub trzydzieści sześć „dekanów”. Cykl sezonowy trwający około 360 dni mógł odpowiadać znakom i dekanom zodiaku, dzieląc każdy znak na trzydzieści części i każdą dekanę na dziesięć części. To dzięki babilońskiemu systemowi liczb sześćdziesiętnych każdy stopień jest podzielony na sześćdziesiąt minut, a każda minuta na sześćdziesiąt sekund.
Menelaos z Aleksandrii (ok. 100 ne) napisał w trzech księgach swoją Sphaerica . W księdze I ustalił podstawę dla trójkątów sferycznych analogiczną do podstawy euklidesowej dla trójkątów płaskich. Ustanawia twierdzenie, które nie ma odpowiednika euklidesowego, że dwa trójkąty sferyczne są przystające, jeśli odpowiadające im kąty są równe, ale nie rozróżnia między trójkątami sferycznymi przystającymi i symetrycznymi. Innym twierdzeniem, które ustalił, jest to, że suma kątów trójkąta sferycznego jest większa niż 180°. Księga II Sphaerica stosuje geometrię sferyczną do astronomii. A Księga III zawiera „twierdzenie Menelaosa”. Dalej podał swoją słynną „zasadę sześciu ilości”.
Później Klaudiusz Ptolemeusz (ok. 90 – ok. 168 ne) rozszerzył w swoim Almagest , czyli Syntaksy Matematyczne, o Akordy Hipparcha w kręgu . Almagest to przede wszystkim praca z astronomii, a astronomia opiera się na trygonometrii. Tablica cięciw Ptolemeusza podaje długości cięciw koła o średnicy 120 w funkcji liczby stopni n w odpowiednim łuku koła, dla n w zakresie od 1/2 do 180 z przyrostem 1/2. Trzynaście ksiąg Almagestu jest najbardziej wpływowym i znaczącym dziełem trygonometrycznym całej starożytności. Twierdzenie, które było centralne dla obliczania akordów przez Ptolemeusza, było znane do dziś jako twierdzenie Ptolemeusza , że suma iloczynów przeciwnych boków cyklicznego czworokąta jest równa iloczynowi przekątnych. Szczególny przypadek twierdzenia Ptolemeusza pojawił się jako propozycja 93 w Danych Euklidesa . Twierdzenie Ptolemeusza prowadzi do odpowiednika czterech formuł na sumę i różnicę dla sinusa i cosinusa, które są dziś znane jako formuły Ptolemeusza, chociaż sam Ptolemeusz używał akordów zamiast sinusa i cosinusa. Ptolemeusz następnie wyprowadził odpowiednik wzoru półkąta
Ptolemeusz wykorzystał te wyniki do stworzenia swoich tabel trygonometrycznych, ale nie można ustalić, czy te tabele pochodzą z pracy Hipparcha.
Ani tablice Hipparcha, ani tablice Ptolemeusza nie przetrwały do dziś, chociaż opisy innych starożytnych autorów nie pozostawiają wątpliwości, że kiedyś istniały.
Pitagoras odkrył wiele właściwości tego, co stało się funkcjami trygonometrycznymi. Pitagorasa , s 2 a + b 2 = H 2 jest przedstawienie podstawowego tożsamości trygonometrycznych sin 2 (x) + cos 2 (x) = 1. Długość 1 przeciwprostokątna trójkąta prostokątnego dowolnej i ma długość nóżki sin (x) i cos(x), gdzie x jest jednym z dwóch nieprostych kątów. Mając to na uwadze, tożsamość, na której opiera się trygonometria, okazuje się twierdzeniem Pitagorasa.
matematyka indyjska
Niektóre z wczesnych i bardzo znaczących osiągnięć trygonometrii miały miejsce w Indiach . Wpływowe dzieła z IV-V wieku naszej ery, znane jako Siddhanty (których było pięć, z których najważniejsza to Surya Siddhanta ) po raz pierwszy zdefiniowały sinus jako współczesną relację między połową kąta a połową akordu, a także definiowanie cosinusa, versine i odwrotnego sinusa . Niedługo potem inny indyjski matematyk i astronom , Aryabhata (476-550 ne), zebrał i rozwinął rozwój Siddhanty w ważnej pracy zwanej Aryabhatiya . Siddhantas i Aryabhatiya zawierać najwcześniejsze przeżyły tabel wartości sinus i versine - wartości cosinus (1), w odstępach 3,75 ° od 0 ° do 90 °, z dokładnością do 4 miejsc po przecinku. Użyli słów jya dla sinusa, kojya dla cosinusa, utkrama-jya dla wersu i otkram jya dla odwrotnego sinusa. Słowa jya i kojya ostatecznie stał sinus i cosinus , odpowiednio po tłumaczeniu opisano powyżej.
W VII wieku Bhaskara I stworzył wzór do obliczania sinusa kąta ostrego bez użycia tabeli. Podał również następującą formułę aproksymacyjną sin( x ), która miała błąd względny mniejszy niż 1,9%:
Później w VII wieku Brahmagupta przekształcił formułę
(również wyprowadzony wcześniej, jak wspomniano powyżej) i wzór interpolacji Brahmagupta do obliczania wartości sinus.
Innym późniejszym indyjskim autorem zajmującym się trygonometrią był Bhaskara II w XII wieku. Bhaskara II opracował trygonometrię sferyczną i odkrył wiele wyników trygonometrycznych.
Bhaskara II był jednym z pierwszych, którzy odkryli i wyniki trygonometryczne, takie jak:
Madhava (ok. 1400) poczynił wczesne postępy w analizie funkcji trygonometrycznych i ich nieskończonych rozwinięciach szeregów . Opracował koncepcje szeregów potęgowych i szeregów Taylora oraz stworzył rozwinięcia szeregów potęgowych dla sinusa, cosinusa, tangensa i arcus tangens. Korzystając z aproksymacji sinusa i cosinusa szeregami Taylora, stworzył tabelę sinusów z dokładnością do 12 miejsc po przecinku i tabelę cosinusów z dokładnością do 9 miejsc po przecinku. Podał także szereg potęgowy π oraz kąt , promień , średnicę i obwód koła w funkcji trygonometrycznej. Jego prace były rozbudowywane przez jego zwolenników w Szkole Kerala do XVI wieku.
| Nie. | Seria | Nazwa | Zachodni odkrywcy serii i przybliżone daty odkrycia |
|---|---|---|---|
| 1 | grzech x = x − x 3 / 3! + x 5 / 5! - x 7 /7! + ... | Seria sinusowa Madhavy | Isaac Newton (1670) i Wilhelm Leibniz (1676) |
| 2 | cos x = 1 − x 2 / 2! + X 4 /4! - x 6 /6! + ... | Cosinus serii Madhavy | Isaac Newton (1670) i Wilhelm Leibniz (1676) |
| 3 | tan −1 x = x − x 3 / 3 + x 5 / 5 − x 7 / 7 + ... | Seria arcus tangens Madhavy | James Gregory (1671) i Wilhelm Leibniz (1676) |
Indyjski tekst Yuktibhāṣā zawiera dowód na rozwinięcie funkcji sinusa i cosinusa oraz wyprowadzenie i dowód szeregu potęgowego dla tangensa odwrotnego , odkryty przez Madhavę. Yuktibhāṣā zawiera również zasady znajdowania sinusów i cosinusów sumy i różnicy dwóch kątów.
Chińska matematyka

W Chinach , Aryabhata „s tabeli sinusa zostały przetłumaczone na chiński matematycznej księdze Kaiyuan Zhanjing , sporządzoną w 718 rne w czasie dynastii Tang . Chociaż Chińczycy przodowali w innych dziedzinach matematyki, takich jak geometria brył, twierdzenie dwumianowe i złożone formuły algebraiczne, wczesne formy trygonometrii nie były tak powszechnie cenione jak we wcześniejszych światach greckich, hellenistycznych, indyjskich i islamskich. Zamiast tego wcześni Chińczycy używali empirycznego substytutu znanego jako chong cha , podczas gdy znane było praktyczne wykorzystanie trygonometrii płaskiej do używania sinusa, tangensa i siecznej. Jednak ten embrionalny stan trygonometrii w Chinach powoli zaczął się zmieniać i rozwijać podczas dynastii Song (960-1279), kiedy chińscy matematycy zaczęli kłaść większy nacisk na potrzebę trygonometrii sferycznej w nauce o kalendarzu i obliczeniach astronomicznych. Erudyta chiński naukowiec, matematyk i oficjalny Shen Kuo (1031-1095) używanych funkcji trygonometrycznych do rozwiązywania problemów matematycznych, akordów i łuków. Victor J. Katz pisze, że we wzorze Shena „technika przecinających się okręgów” stworzył przybliżenie łuku s okręgu, biorąc pod uwagę średnicę d , strzałkę v , i długość c cięciwy stanowiącej łuk, którego długość w przybliżeniu jako
Sal Restivo pisze, że prace Shena dotyczące długości łuków koła stały się podstawą trygonometrii sferycznej opracowanej w XIII wieku przez matematyka i astronoma Guo Shoujinga (1231–1316). Jak twierdzą historycy L. Gauchet i Joseph Needham, Guo Shoujing używał w swoich obliczeniach trygonometrii sferycznej, aby ulepszyć system kalendarza i chińską astronomię . Wraz z późniejszą XVII-wieczną chińską ilustracją matematycznych dowodów Guo, Needham stwierdza, że:
Guo użył czworokątnej kulistej piramidy, której podstawowy czworobok składał się z jednego łuku równikowego i jednego ekliptyki, wraz z dwoma łukami południkowymi , z których jeden przechodził przez punkt przesilenia letniego ... Dzięki takim metodom był w stanie uzyskać du lü (stopnie równika odpowiadające stopniom ekliptyki), ji cha (wartości akordów dla danych łuków ekliptyki) oraz cha lü (różnica między akordami łuków różniąca się o 1 stopień).
Pomimo osiągnięć pracy Shena i Guo w dziedzinie trygonometrii, kolejna ważna praca z chińskiej trygonometrii nie została opublikowana ponownie do 1607 roku, z podwójną publikacją Elementów Euklidesa przez chińskiego urzędnika i astronoma Xu Guangqi (1562-1633) oraz włoskiego jezuitę Matteo Ricciego (1552-1610).
Średniowieczny świat islamski

Wcześniejsze prace były później tłumaczone i rozszerzane w średniowiecznym świecie islamskim przez muzułmańskich matematyków, głównie pochodzenia perskiego i arabskiego , którzy ogłosili dużą liczbę twierdzeń, które uwolniły przedmiot trygonometrii od zależności od pełnego czworoboku , jak to miało miejsce w matematyce hellenistycznej z powodu do zastosowania twierdzenia Menelaosa . Według ES Kennedy'ego to właśnie po tym rozwoju matematyki islamu „pojawiła się pierwsza prawdziwa trygonometria w tym sensie, że dopiero wtedy obiektem badań stał się trójkąt sferyczny lub płaski , jego boki i kąty ”.
Znane były również metody dotyczące trójkątów sferycznych, w szczególności metoda Menelaosa z Aleksandrii , który opracował „twierdzenie Menelaosa” do rozwiązywania problemów sferycznych. Jednak ES Kennedy zwraca uwagę, że chociaż w matematyce przedislamskiej było możliwe obliczenie wielkości figury sferycznej, w zasadzie przy użyciu tablicy akordów i twierdzenia Menelaosa, zastosowanie tego twierdzenia do problemów sferycznych było bardzo trudne w praktyce. W celu obchodzenia świąt w kalendarzu islamskim, w którym czasy wyznaczane były przez fazy księżyca , astronomowie początkowo stosowali metodę Menelaosa do obliczania miejsca księżyca i gwiazd , choć metoda ta okazała się niezręczna i trudna. Polegało to na ustawieniu dwóch przecinających się trójkątów prostokątnych ; stosując twierdzenie Menelaosa można było rozwiązać jedną z sześciu stron, ale tylko wtedy, gdy znanych było pięć pozostałych stron. Aby powiedzieć raz od słońca „s wysokości , na przykład, powtarzane zastosowania Menelaosa” Twierdzenie były wymagane. Dla średniowiecznych astronomów islamskich było oczywistym wyzwaniem znalezienie prostszej metody trygonometrycznej.
Na początku IX wieku ne Muhammad ibn Mūsā al-Chwārizmī stworzył dokładne tablice sinusów i cosinusów oraz pierwszą tablicę stycznych. Był także pionierem w trygonometrii sferycznej . W 830 r. Habash al-Hasib al-Marwazi stworzył pierwszą tablicę cotangensów. Muhammad ibn Jabir al-Harrānī al-Battānī (Albatenius) (853-929 ne) odkrył wzajemne funkcje siecznej i cosecans i stworzył pierwszą tablicę cosecans dla każdego stopnia od 1° do 90°.
W X wieku naszej ery, w pracy Abū al-Wafā' al-Būzjāni , muzułmańscy matematycy używali wszystkich sześciu funkcji trygonometrycznych . Abu al-Wafa posiadał tablice sinusów w przyrostach co 0,25°, z dokładnością do 8 miejsc po przecinku oraz dokładne tablice wartości stycznych. Opracował również następujący wzór trygonometryczny:
- (szczególny przypadek wzoru Ptolemeusza dodawania kąta; patrz wyżej)
W swoim oryginalnym tekście Abū al-Wafā' stwierdza: „Jeśli tego chcemy, mnożymy dany sinus przez cosinus minut i otrzymujemy połowę sinusa podwójnego”. Abū al-Wafā ustanowił również dodawanie kątów i tożsamości różnicowe przedstawione z kompletnymi dowodami:
Dla drugiego z nich tekst stwierdza: „Mnożymy sinus każdego z dwóch łuków przez cosinus pozostałych minut . Jeśli chcemy uzyskać sinus sumy, dodajemy iloczyny, jeśli chcemy uzyskać sinus różnicy , bierzemy ich różnicę”.
Odkrył również prawo sinusów dla trygonometrii sferycznej:
Również pod koniec X i na początku XI wieku ne egipski astronom Ibn Yunus wykonał wiele dokładnych obliczeń trygonometrycznych i wykazał następującą tożsamość trygonometryczną :
Al-Jayyani (989-1079) z al-Andalus napisał Księgę nieznanych łuków sfery , która jest uważana za „pierwszy traktat o trygonometrii sferycznej ”. „Zawiera wzory na trójkąty prawoskrętne , ogólne prawo sinusów i rozwiązanie trójkąta sferycznego za pomocą trójkąta biegunowego”. Ten traktat miał później „silny wpływ na matematykę europejską”, a jego „definicja stosunków jako liczb” i „metoda rozwiązywania sferycznego trójkąta, gdy wszystkie boki są nieznane” prawdopodobnie wpłynęły na Regiomontanus .
Metoda triangulacji została po raz pierwszy opracowana przez muzułmańskich matematyków, którzy zastosowali ją do praktycznych zastosowań, takich jak geodezja i geografia islamu , jak opisał Abu Rayhan Biruni na początku XI wieku. Sam Biruni wprowadził techniki triangulacji do pomiaru wielkości Ziemi i odległości między różnymi miejscami. Pod koniec XI wieku Omar Khayyám (1048–1131) rozwiązywał równania sześcienne za pomocą przybliżonych rozwiązań numerycznych znalezionych przez interpolację w tabelach trygonometrycznych. W XIII wieku Nasir al-Dīn al-Tūsī jako pierwszy potraktował trygonometrię jako dyscyplinę matematyczną niezależną od astronomii i rozwinął trygonometrię sferyczną do jej obecnej postaci. Wymienił sześć odrębnych przypadków trójkąta prostokątnego w trygonometrii sferycznej, a w swoim O figurze sektorowej stwierdził prawo sinusów dla trójkątów płaskich i sferycznych, odkrył prawo stycznych dla trójkątów sferycznych i dostarczył dowodów dla obu te prawa. Nasir al-Din al-Tusi został opisany jako twórca trygonometrii jako samodzielnej dyscypliny matematycznej.
W XV wieku Jamshīd al-Kāshī przedstawił pierwsze wyraźne stwierdzenie prawa cosinusów w formie odpowiedniej do triangulacji . We Francji prawo cosinusów jest nadal określane jako twierdzenie Al-Kashi . Podał również tablice trygonometryczne wartości funkcji sinus do czterech cyfr sześćdziesiętnych (odpowiednik 8 miejsc po przecinku) dla każdego 1° argumentu z różnicami dodanymi dla każdej 1/60 z 1°. Ulugh Beg podaje również dokładne tabele sinusów i stycznych z dokładnością do 8 miejsc po przecinku mniej więcej w tym samym czasie.
renesans europejski i później
W 1342 Levi ben Gershon, znany jako Gersonides , napisał O sinusach, akordach i łukach , w szczególności udowadniając prawo sinusów dla płaskich trójkątów i podając pięciocyfrowe tablice sinusowe .
Uproszczona tablica trygonometryczna, " toleta de marteloio ", była używana przez żeglarzy na Morzu Śródziemnym w XIV-XV wieku do obliczania kursów nawigacyjnych . Został opisany przez Ramona Llulla z Majorki w 1295 r. i przedstawiony w atlasie weneckim kapitana Andrei Bianco z 1436 r .
Regiomontanus był prawdopodobnie pierwszym matematykiem w Europie, który potraktował trygonometrię jako odrębną dyscyplinę matematyczną, w swoim De triangulis omnimodis napisanym w 1464 roku, a także w późniejszym Tabulae direction, który zawierał nienazwaną funkcję styczną. Opus Palatinum de triangulis od Jerzy Joachim Retyk , ucznia Kopernika , był prawdopodobnie pierwszym w Europie do definiowania funkcji trygonometrycznych bezpośrednio pod względem odpowiednich trójkątów zamiast okręgów, z tabel dla wszystkich sześciu funkcji trygonometrycznych; dzieło to zostało ukończone przez ucznia Retyka Valentina Otho w 1596 roku.
W XVII wieku Isaac Newton i James Stirling opracowali ogólny wzór interpolacji Newtona-Stirlinga dla funkcji trygonometrycznych.
W 18 wieku, Leonhard Euler „s Wprowadzenie w infinitorum analysin (1748) był głównie odpowiedzialny za opracowanie analityczne traktowania funkcji trygonometrycznych w Europie, czerpiąc swoje nieskończone serie i prezentacji« Wzór Eulera » e ix = cos x + i sin x . Euler użył niemal nowoczesnych skrótów sin. , co . , tg. , łóżeczko. , ust. i cosek. Wcześniej Roger Cotes obliczył pochodną sinusa w swoim Harmonia Mensurarum (1722). Również w XVIII wieku Brook Taylor zdefiniował ogólny szereg Taylora i podał rozwinięcia i aproksymacje szeregu dla wszystkich sześciu funkcji trygonometrycznych. Duży wpływ na rozwój serii trygonometrycznych miały również prace Jamesa Gregory'ego z XVII wieku i Colina Maclaurina z XVIII wieku.
Zobacz też
- matematyka grecka
- Historia matematyki
- Funkcje trygonometryczne
- Trygonometria
- Tabela akordów Ptolemeusza
- Tablica sinusowa Aryabhaty
- Racjonalna trygonometria
Cytaty i przypisy
Bibliografia
- Boyer, Carl Benjamin (1991). Historia matematyki (2nd ed.). John Wiley & Sons, Inc. ISBN 978-0-471-54397-8.
- Gauchet, L. (1917). Uwaga Sur La Trigonométrie Sphérique de Kouo Cheou-King .
- Józef, George G. (2000). Herb Peacock: Non-European Roots of Mathematics (2nd ed.). Londyn: Książki o pingwinach . Numer ISBN 978-0-691-00659-8.
- Katz, Victor J. (1998). Historia matematyki / Wprowadzenie (wyd. 2). Addisona Wesleya. Numer ISBN 978-0-321-01618-8.
- Katz, Victor J. (2007). Matematyka Egiptu, Mezopotamii, Chin, Indii i islamu: podręcznik źródłowy . Princeton: Wydawnictwo Uniwersytetu Princeton. Numer ISBN 978-0-691-11485-9.
- Needham, Józef (1986). Nauka i cywilizacja w Chinach: Tom 3, Matematyka i nauki o niebie i ziemi . Tajpej: Jaskinie Książki, Ltd.
- Restivo, Sal (1992). Matematyka w społeczeństwie i historii: dociekania socjologiczne . Dordrecht: Wydawnictwo Akademickie Kluwer. Numer ISBN 1-4020-0039-1.
Dalsza lektura
- Anton von Braunmühl (1903) Vorlesungen über Geschichte der Trigonometrie , za pośrednictwem archiwum internetowego