Sześciokątny plaster miodu - Heptagonal tiling honeycomb
| Sześciokątny plaster miodu z płytek | |
|---|---|
| Rodzaj | Zwykły plaster miodu |
| Symbol Schläfli | {7,3,3} |
| Diagram Coxetera |
|
| Komórki |
{7,3} 
|
| Twarze | Heptagon {7} |
| Figura wierzchołka | czworościan {3,3} |
| Podwójny | {3,3,7} |
| Grupa Coxetera | [7,3,3] |
| Nieruchomości | Regularny |
W geometrii o hiperbolicznej przestrzeni 3-wymiarowej , w siedmiokątnych układanie plastra miodu lub 7,3,3 plastra miodu regularnie, wypełniającymi przestrzeń teselacji (lub o strukturze plastra miodu ). Każda nieskończona komórka składa się z heptagonalnej płytki, której wierzchołki leżą na 2-hipercyklu , z których każda ma ograniczający okrąg na idealnej kuli.
Geometria
Symbol schläfliego z siedmiokątnych układanie plastra miodu, {7,3,3} w trzy siedmiokątnych Tilings spotkanie na każdej krawędzi. Postać wierzchołka tej strukturze plastra miodu jest Tetrahedron {3,3}.
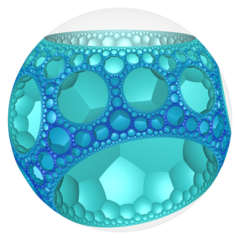 Model dysku Poincaré (wyśrodkowany na wierzchołku) |
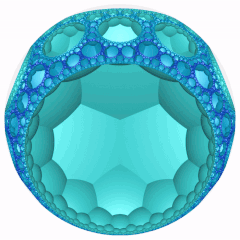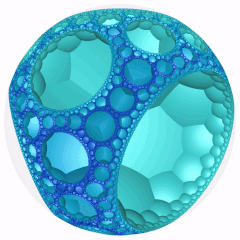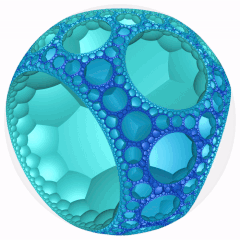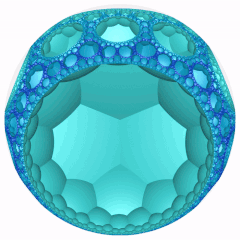 Obracanie |
 Idealna powierzchnia |
Powiązane polytopy i plastry miodu
Jest częścią serii regularnych polytopów i plastrów miodu z symbolem { p , 3,3} Schläfli i czworościennymi figurami wierzchołkowymi :
| {p, 3,3} plastry miodu | ||||||||
|---|---|---|---|---|---|---|---|---|
| Przestrzeń | S 3 | H 3 | ||||||
| Formularz | Skończone | Paracompact | Niekompaktowy | |||||
| Nazwa | {3,3,3} | {4,3,3} | {5,3,3} | {6,3,3} | {7,3,3} | {8,3,3} | ... {∞, 3,3} | |
| Wizerunek |

|

|

|

|

|

|

|
|
Diagramy Coxetera 
|
1 |
|
|
|
|
|
|
|
| 4 |
|
|
|
|
||||
| 6 |
|
|
|
|
||||
| 12 |
|
|
|
|
||||
| 24 |
|
|
|
|
||||
| Komórki {p, 3} |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞, 3} |
|
Jest częścią serii regularnych plastrów miodu, {7,3, p }.
| {7,3,3} | {7,3,4} | {7,3,5} | {7,3,6} | {7,3,7} | {7,3,8} | ... {7,3, ∞} |
|---|---|---|---|---|---|---|
|
|

|

|

|

|

|
Jest częścią serii regularnych plastrów miodu z {7, p , 3}.
| {7,3,3} | {7,4,3} | {7,5,3} ... |
|---|---|---|

|

|

|
Ośmiokątna płytka o strukturze plastra miodu
| Ośmiokątny plaster miodu z płytek | |
|---|---|
| Rodzaj | Zwykły plaster miodu |
| Symbol Schläfli | {8,3,3} t {8,4,3} 2t {4,8,4} t {4 [3,3] } |
| Diagram Coxetera |
|
| Komórki |
{8,3} 
|
| Twarze | Ośmiokąt {8} |
| Figura wierzchołka | czworościan {3,3} |
| Podwójny | {3,3,8} |
| Grupa Coxetera | [8,3,3] |
| Nieruchomości | Regularny |
W geometrii o hiperbolicznej przestrzeni 3-wymiarowej , w ośmiokątnym układanie plastra miodu lub 8,3,3 plastra miodu regularnie, wypełniającymi przestrzeń teselacji (lub o strukturze plastra miodu ). Każda nieskończona komórka składa się z ośmiokątnych płytek, których wierzchołki leżą na 2-hipercyklu , z których każdy ma ograniczający okrąg na idealnej kuli.
Symbol schläfliego ośmiokątnej układanie plastra miodu, {8,3,3} w trzy ośmiokątne Tilings spotkanie na każdej krawędzi. Postać wierzchołka tej strukturze plastra miodu jest Tetrahedron {3,3}.
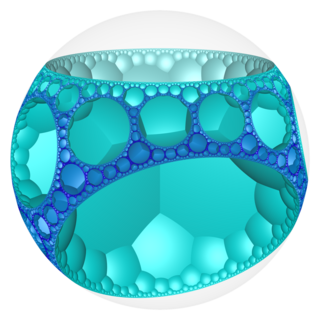 Model dysku Poincaré (wyśrodkowany na wierzchołku) |
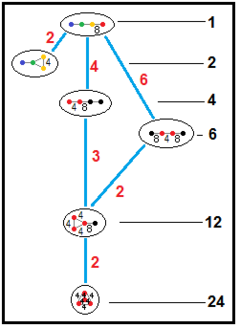 Bezpośrednie podgrupy [8,3,3] |
Płytki o strukturze plastra miodu
| Płytka o strukturze plastra miodu Apeirogonal | |
|---|---|
| Rodzaj | Zwykły plaster miodu |
| Symbol Schläfli | {∞, 3,3} t {∞, 3,3} 2t {∞, ∞, ∞} t {∞ [3,3] } |
| Diagram Coxetera |
|
| Komórki |
{∞, 3} 
|
| Twarze | Apeirogon {∞} |
| Figura wierzchołka | czworościan {3,3} |
| Podwójny | {3,3, ∞} |
| Grupa Coxetera | [∞, 3,3] |
| Nieruchomości | Regularny |
W geometrii o hiperbolicznej przestrzeni 3-wymiarowej , w apeirogonal plastra miodu układanie lub ∞, 3,3 plastra miodu regularnie, wypełniającymi przestrzeń tesselacji (lub o strukturze plastra miodu ). Każda nieskończona komórka składa się z apeirogonalnych płytek, których wierzchołki leżą na 2-hipercyklu , z których każdy ma ograniczający okrąg na idealnej kuli.
Symbol schläfliego z apeirogonal układanie plastra miodu, {∞, 3,3}, z trzema apeirogonal Tilings spotkanie na każdej krawędzi. Postać wierzchołka tej strukturze plastra miodu jest Tetrahedron {3,3}.
Projekcja „idealnej powierzchni” poniżej to płaszczyzna w nieskończoności w modelu półprzestrzeni Poincarego H3. Przedstawia apolliński układ uszczelek złożony z okręgów wewnątrz największego koła.
 Model dysku Poincaré (wyśrodkowany na wierzchołku) |
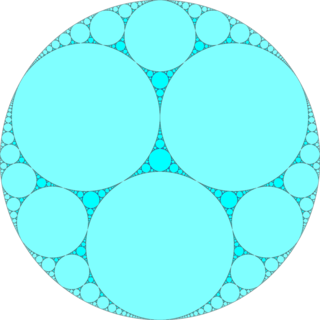 Idealna powierzchnia |
Zobacz też
Bibliografia
- Coxeter , Regular Polytopes , 3rd. red., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabele I i II: Regularne polytopes and honeycombs, str. 294–296)
- Piękno geometrii: dwanaście esejów (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (rozdział 10, Regular Honeycombs in Hyperbolic Space ) Tabela III
- Jeffrey R. Weeks The Shape of Space, wydanie 2 ISBN 0-8247-0709-5 (rozdziały 16–17: Geometrie na trzech rozmaitościach I, II)
- George Maxwell, Sphere Packings and Hyperbolic Reflection Groups , JOURNAL OF ALGEBRA 79, 78-97 (1982) [1]
- Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings , (2013) [2]
- Wizualizacja hiperbolicznych plastrów miodu arXiv: 1511.02851 Roice Nelson, Henry Segerman (2015)
Linki zewnętrzne
- John Baez , Wizualne spostrzeżenia : {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
- Danny Calegari , Kleinian, narzędzie do wizualizacji grup Kleinian, Geometry and the Imagination 4 marca 2014 r. [3]
