Kostka - Cube
| Sześcian regularny | |
|---|---|
 (Kliknij tutaj, aby zobaczyć model obrotowy) |
|
| Rodzaj | Bryła platońska |
| krótki kod | 4= |
| Elementy |
F = 6, E = 12 V = 8 (χ = 2) |
| Twarze po bokach | 6{4} |
| notacja Conway | C |
| Symbole Schläfli | {4,3} |
| t{2,4} lub {4}×{} tr{2,2} lub {}×{}×{} |
|
| Konfiguracja twarzy | V3.3.3.3 |
| Symbol Wythoffa | 3 | 2 4 |
| Schemat Coxetera |
|
| Symetria | O h , B 3 , [4,3], (*432) |
| Grupa rotacyjna | O , [4,3] + , (432) |
| Bibliografia | U 06 , C 18 , W 3 |
| Nieruchomości | regularne , wypukłe zonohedron |
| Kąt dwuścienny | 90° |
 4.4.4 ( rysunek wierzchołka ) |
 Oktaedron ( podwójny wielościan ) |
 Internet |
|
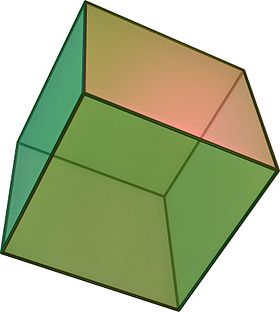
W geometrii , A kostka jest trójwymiarowy obcy przedmiot ograniczony przez sześć kwadratowych twarzy, faset lub stron, z trzema spotkania w każdym wierzchołku .
Sześcian jest jedyną regularny sześciokąt i jest jednym z pięciu brył platońskich . Ma 6 ścian, 12 krawędzi i 8 wierzchołków.
Sześcian jest również kwadratowym równoległościanem , równobocznym prostopadłościanem i prawym romboedrem . Jest to regularny graniastosłup kwadratowy w trzech orientacjach i trójkątny trapezon w czterech orientacjach.
Sześcian jest podwójny do ośmiościanu . Ma symetrię sześcienną lub oktaedryczną .
Sześcian jest jedynym wypukłym wielościanem, którego ściany są same kwadratami .
Rzuty prostopadłe
Kostka ma cztery specjalne występy prostokątne , skupione na wierzchołku, krawędzie twarzy i prostopadłej do jej wierzchołka rysunku . Pierwsza i trzecia odpowiadają samolotom Coxetera A 2 i B 2 .
| Wyśrodkowany przez | Twarz | Wierzchołek |
|---|---|---|
| Samoloty Coxetera |
B 2
|
2
|
Symetria projekcyjna |
[4] | [6] |
| Przechylone widoki |
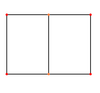
|

|
Dachówka sferyczna
Sześcian może być również reprezentowany jako sferyczne płytki i rzutowany na płaszczyznę za pomocą projekcji stereograficznej . Ta projekcja jest konforemna , zachowując kąty, ale nie powierzchnie lub długości. Linie proste na sferze są rzutowane na płaszczyznę jako łuki kołowe.

|

|
| Rzut prostokątny | Projekcja stereograficzna |
|---|
współrzędne kartezjańskie
W przypadku sześcianu wyśrodkowanego na początku, z krawędziami równoległymi do osi i długości krawędzi 2, współrzędne kartezjańskie wierzchołków są
- (±1, ±1, ±1)
natomiast wnętrze składa się ze wszystkich punktów ( x 0 , x 1 , x 2 ) z -1 < x i < 1 dla wszystkich i .
Równanie w
W geometrii analitycznej powierzchnia sześcianu o środku ( x 0 , y 0 , z 0 ) i długości krawędzi 2a jest miejscem wszystkich punktów ( x , y , z ) takich, że
Sześcian można również uznać za przypadek graniczny superelipsoidy 3D, ponieważ wszystkie trzy wykładniki zbliżają się do nieskończoności.
Formuły
Dla sześcianu o długości krawędzi :
| powierzchnia | Tom | ||
| przekątna ściany | przekątna przestrzeni | ||
| promień kuli opisanej | promień sfery stycznej do krawędzi | ||
| promień wpisanej kuli | kąty między ścianami (w radianach ) |
Ponieważ objętość sześcianu jest trzecią potęgą jego boków , trzecie potęgi nazywane są sześcianami , przez analogię do kwadratów i drugich potęg.
Sześcian ma największą objętość wśród prostopadłościanów (prostokątnych pudełek) o danej powierzchni . Ponadto sześcian ma największą objętość wśród prostopadłościanów o tym samym całkowitym rozmiarze liniowym (długość+szerokość+wysokość).
Punkt w przestrzeni
Dla sześcianu, którego opisująca sfera ma promień R , oraz dla danego punktu w jego trójwymiarowej przestrzeni o odległości d i od ośmiu wierzchołków sześcianu, mamy:
Podwojenie kostki
Podwojenie sześcianu , czyli problem Delian , to problem starożytnych matematyków greckich polegający na używaniu tylko cyrkla i linijki do rozpoczęcia od długości krawędzi danego sześcianu i skonstruowania długości krawędzi sześcianu z podwojoną długością sześcianu. objętość oryginalnej kostki. Nie byli w stanie rozwiązać tego problemu, aw 1837 Pierre Wantzel udowodnił, że jest to niemożliwe, ponieważ pierwiastek sześcienny z 2 nie jest liczbą konstruktywną .
Jednolita kolorystyka i symetria
Sześcian ma trzy jednolite kolory, nazwane kolorami kwadratów wokół każdego wierzchołka: 111, 112, 123.
Sześcian ma cztery klasy symetrii, które mogą być reprezentowane przez przechodnie wierzchołkowe kolorowanie ścian. Najwyższa ośmiościenny symetria O h ma wszystkie twarze tego samego koloru. Dwuścienny symetria D 4h pochodzi z kostki będącego pryzmat, ze wszystkie cztery boki są tego samego koloru. Podzbiory pryzmatyczne D 2d mają taki sam kolor jak poprzedni, a D 2h ma naprzemienne kolory boków, w sumie trzy kolory, sparowane przeciwległymi bokami. Każda forma symetrii ma inny symbol Wythoffa .
| Nazwa | Sześcian regularny |
Pryzmat kwadratowy | Trapezopryzm prostokątny |
Prostokątny prostopadłościan |
Pryzmat rombowy |
Trapezoedr trójkątny |
|---|---|---|---|---|---|---|
|
Schemat Coxetera |
|
|
|
|
|
|
|
Symbol Schläfli |
{4,3} | {4}×{} rr{4,2} |
z 2 {2,4} | { } 3 tr{2,2} |
{}×2{} | |
|
Symbol Wythoffa |
3 | 4 2 | 4 2 | 2 | 2 2 2 | | |||
| Symetria | O h [4,3] (*432) |
D 4h [4,2] (*422) |
D 2d [4,2 + ] (2*2) |
D 2h [2,2] (*222) |
D 3d [6,2 + ] (2*3) |
|
Kolejność symetrii |
24 | 16 | 8 | 8 | 12 | |
| Obraz (jednolita kolorystyka) |
 (111) |
 (112) |
 (112) |
 (123) |
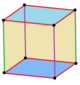 (112) |
 (111), (112) |
Relacje geometryczne

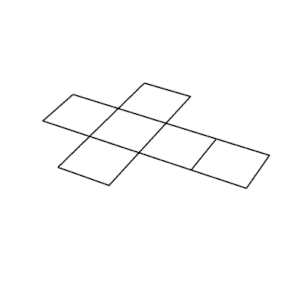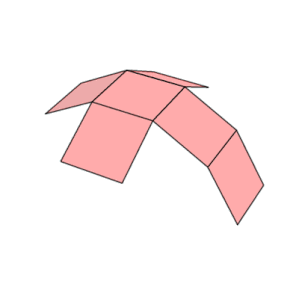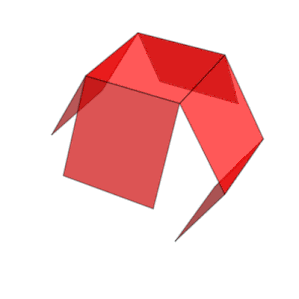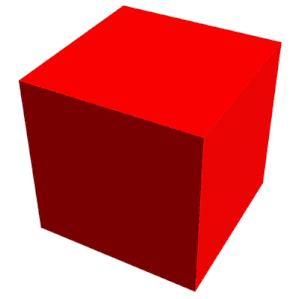
Sześcian ma jedenaście siatek (jedna pokazana powyżej): oznacza to, że istnieje jedenaście sposobów na spłaszczenie pustego sześcianu poprzez przecięcie siedmiu krawędzi. Aby pokolorować sześcian tak, aby żadne dwie sąsiadujące ściany nie miały tego samego koloru, potrzeba co najmniej trzech kolorów.
Sześcian jest komórką jedynej regularnej płytki trójwymiarowej przestrzeni euklidesowej . Wśród brył platońskich wyróżnia się także tym, że posiada ściany o parzystej liczbie boków, a co za tym idzie, jest jedynym członkiem tej grupy, który jest zonohedronem (każda ściana ma symetrię punktową).
Kostkę można pociąć na sześć identycznych ostrosłupów kwadratowych . Jeśli te kwadratowe piramidy są następnie dołączone do ścian drugiego sześcianu, otrzymuje się dwunastościan rombowy (z parami trójkątów współpłaszczyznowych połączonymi w ściany rombowe).
Inne wymiary
Analog sześcianu w czterowymiarowej przestrzeni euklidesowej ma specjalną nazwę – teserakt lub hipersześcian . Dokładniej, hipersześcian (lub n -wymiarowy sześcian lub po prostu n -sześcian) jest odpowiednikiem sześcianu w n -wymiarowej przestrzeni euklidesowej, a teserakt jest hipersześcianem 4 rzędu. Hipersześcian jest również nazywany politopem miar .
Istnieją również odpowiedniki sześcianu w niższych wymiarach: punkt w wymiarze 0, odcinek linii w jednym wymiarze i kwadrat w dwóch wymiarach.
Powiązane wielościany

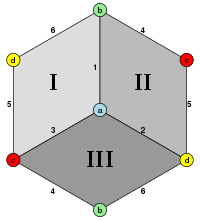
Iloraz sześcianu przez antypodyczne mapie daje rzutowe wielościan , na hemicube .
Jeśli oryginalny sześcian ma długość krawędzi 1, jego podwójny wielościan ( oktaedr ) ma długość krawędzi .
Sześcian jest przypadkiem szczególnym w różnych klasach wielościanów ogólnych:
| Nazwa | Równe długości krawędzi? | Równe kąty? | Kąty proste? |
|---|---|---|---|
| Sześcian | tak | tak | tak |
| Rhombohedron | tak | tak | Nie |
| Prostopadłościan | Nie | tak | tak |
| Równoległościan | Nie | tak | Nie |
| czworobocznie zwrócony sześcian | Nie | Nie | Nie |
Wierzchołki sześcianu można podzielić na dwie grupy po cztery, z których każda tworzy regularny czworościan ; bardziej ogólnie jest to określane jako demicube . Te dwa razem tworzą regularny związek , Stella octgula . Przecięcie tych dwóch form tworzy ośmiościan foremny. Symetrie czworościanu foremnego odpowiadają symetriom sześcianu, które odwzorowują każdy czworościan do siebie; pozostałe symetrie sześcianu odwzorowują je nawzajem.
Jeden taki czworościan foremny ma objętość 1/3tego sześcianu. Pozostała przestrzeń składa się z czterech równych nieregularnych czworościanów o objętości1/6 sześcianu, każdy.
Spirytus kostka jest sześcio-ośmiościan . Jeśli odetniemy mniejsze rogi, otrzymamy wielościan o sześciu ścianach ośmiokątnych i ośmiu trójkątnych. W szczególności możemy otrzymać ośmiokąty foremne ( sześcian ścięty ). Sześcio-ośmiościan rombowy mały uzyskuje się przez odcięcie obu naroży i krawędzi do odpowiedniej kwoty.
Sześcian może być wpisany w dwunastościan tak, że każdy wierzchołek sześcianu jest wierzchołkiem dwunastościanu, a każda krawędź jest przekątną jednej ze ścian dwunastościanu; wzięcie wszystkich takich kostek daje początek regularnemu złożeniu pięciu sześcianów.
Jeśli dwa przeciwległe rogi sześcianu zostaną ścięte na głębokości trzech wierzchołków bezpośrednio z nimi połączonych, otrzymamy nieregularny ośmiościan. Osiem z tych nieregularnych ośmiościanów można przymocować do trójkątnych ścian ośmiościanu foremnego, aby uzyskać sześcian.
Sześcian jest topologicznie powiązany z serią sferycznych wielościanów i płytek z figurami wierzchołków rzędu 3 .
| * n 32 mutacja symetrii regularnych płytek: { n ,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kulisty | Euklidesa | Kompaktowa hiperb. | Parako. | Niekompaktowy hiperboliczny | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
Sześcian należy do rodziny wielościanów jednorodnych spokrewnionych z sześcianem i ośmiościanem foremnym.
| Jednolite wielościany ośmiościenne | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symetria : [4,3], (*432) | [4,3] + (432) |
[1 + ,4,3] = [3,3] (*332) |
[3 + ,4] (3*2) |
|||||||
| {4,3} | t{4,3} |
r{4,3} r{3 1,1 } |
t{3,4} t{3 1,1 } |
{3,4} {3 1,1 } |
rr{4,3} s 2 {3,4} |
tr{4,3} | sr{4,3} |
godz.{4,3} {3,3} |
h 2 {4,3} t{3,3} |
s{3,4} s{3 1,1 } |
|
|
|
|
|
|
|
|
|
|
||
|
= |
= |
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
| Duals do jednolitych wielościanów | ||||||||||
| V4 3 | V3.8 2 | V(3.4) 2 | V4.6 2 | V3 4 | V3.4 3 | Wersja 4.6.8 | V3 4 0,4 | V3 3 | V3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Sześcian jest powiązany topologicznie jako część ciągu regularnych kafelków, rozciągających się na płaszczyznę hiperboliczną : {4,p}, p=3,4,5...
| * n 42 mutacja symetrii regularnych płytek: {4, n } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kulisty | Euklidesa | Kompaktowy hiperboliczny | Parakompaktowy | ||||||||
 {4,3} |
 {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} ... |
 {4,∞} |
|||||
Przy symetrii dwuściennej , Dih 4 , sześcian jest topologicznie powiązany w serii jednolitych wielościanów i kafelków 4.2n.2n, rozciągających się do płaszczyzny hiperbolicznej:
| * n 42 mutacja symetrii przyciętych płytek: 4,2 n .2 n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symetria * n 42 [n,4] |
Kulisty | Euklidesa | Kompaktowy hiperboliczny | Parakomp. | |||||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
||||
| Obcięte cyfry |

|

|

|

|

|

|

|

|
|||
| Konfig. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
figurki n-kis |

|

|

|

|

|

|

|

|
|||
| Konfig. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
Wszystkie te figury mają symetrię oktaedryczną .
Sześcian jest częścią ciągu wielościanów rombowych i kafelków o symetrii grupy Coxetera [ n ,3] . Sześcian może być postrzegany jako rombowy sześcian, gdzie romb to kwadraty.
| Mutacje symetrii podwójnych płytek quasiregularnych : V(3.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | Kulisty | Euklidesa | Hiperboliczny | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Dekarstwo |

|

|

|

|

|

|

|
||||
| Konf. | V(3.3) 2 | V(3.4) 2 | V(3.5) 2 | V(3.6) 2 | V(3.7) 2 | V(3.8) 2 | V(3.∞) 2 | ||||
Kostka to graniastosłup kwadratowy :
| Nazwa pryzmatu | Pryzmat dwukątny | (Trigonal) Trójkątny pryzmat |
(czworokątny) pryzmat kwadratowy |
Graniastosłup pięciokątny | Sześciokątny pryzmat | Graniastosłup siedmiokątny | Pryzmat ośmiokątny | Pryzmat enneagonalny | Graniastosłup dziesięciokątny | Pryzmat heksagonalny | Pryzmat dwunastokątny | ... | Pryzmat apeirogonalny |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obraz wielościanu |
|
|
|
|
|
|
|
|
|
|
|
... | |
| Kulisty obraz kafelkowy |
|
|
|
|
|
|
|
|
Samolot kafelkowy obraz |
|
|||
| Konfiguracja wierzchołków. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | ... | .4.4 |
| Schemat Coxetera |
|
|
|
|
|
|
|
|
|
|
|
... |
|
Jako trójkątny trapezhedron sześcian jest powiązany z rodziną symetrii heksagonalnej dwuściennej.
| Jednolite sześciokątne dwuścienne sferyczne wielościany | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symetria : [6,2] , (*622) | [6,2] + , (622) | [6,2 + ], (2*3) | ||||||||||||

|
|

|

|

|
|

|

|

|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| Podwójne do mundurów | ||||||||||||||

|

|

|

|

|

|

|

|

|
||||||
| V6 2 | V12 2 | V6 2 | V4.4.6 | V2 6 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
 Związek trzech kostek |
 Związek pięciu kostek |
W jednolitych plastrach miodu i polichora
Jest elementem 9 z 28 wypukłych jednolitych plastrów miodu :
Jest również elementem pięciu jednorodnych czterowymiarowych polichor :
|
Teserakt |
Kantelowany 16-ogniwowy |
Runcinated tesseract |
Cantitruncated 16-komorowy |
Runcitruncated 16-komorowy |

|

|
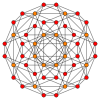
|

|

|
Wykres sześcienny
| Wykres sześcienny | |
|---|---|
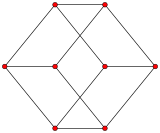 | |
| Nazwany po | P 3 |
| Wierzchołki | 8 |
| Krawędzie | 12 |
| Promień | 3 |
| Średnica | 3 |
| Obwód | 4 |
| Automorfizmy | 48 |
| Liczba chromatyczna | 2 |
| Nieruchomości | Hamiltonian , regularny , symetryczny , odległościowo regularny , odległościowo przechodni , 3-wierzchołkowy , dwudzielny , planarny graf |
| Tabela wykresów i parametrów | |
Szkielet sześcianu (wierzchołki oraz krawędzie) tworzą wykres , 8 i 12 wierzchołków krawędzi. Jest to szczególny przypadek grafu hipersześcianowego . Jest to jeden z 5 grafów platońskich , z których każdy jest szkieletem platońskiej bryły .
Rozszerzeniem jest trójwymiarowy k- ary graf Hamminga , który dla k = 2 jest grafem sześciennym. Wykresy tego rodzaju występują w teorii przetwarzania równoległego w komputerach.
Zobacz też
Bibliografia
Zewnętrzne linki
- Weisstein, Eric W. "Cube" . MatematykaŚwiat .
- Kostka: Interaktywny model wielościanu *
- Objętość sześcianu z interaktywną animacją
- Kostka (strona Roberta Webba)