Trapezoedr trójkątny ścięty - Truncated triangular trapezohedron
| Ścięty trójkątny trapezohedron Bryła Dürera |
|
|---|---|
|
|
| Rodzaj | Trapezohedron ścięty |
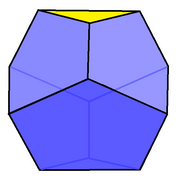
| Twarze | 6 pięciokątów , 2 trójkąty |
| Krawędzie | 18 |
| Wierzchołki | 12 |
| Grupa symetrii | D 3d , [2 + ,6], (2*3) |
| Podwójny wielościan | Dwupiramida trójkątna żyro-wydłużona |
| Nieruchomości | wypukły |
W geometrii The obcinane trójkątny trapezohedron jest pierwszym w nieskończonym szeregu obcinane trapezohedron wielościany. Ma 6 pięciokątnych i 2 trójkątne twarze.
Geometria
Ten wielościan może być wykonana przez obcinanie dwa przeciwległe wierzchołki o sześcianu , o trójkątny trapezohedron (wypukły wielościan z sześciu przystających rombów boki, utworzone w wyniku rozciągania i kurczenia się kostki wzdłuż jednej ze swoich dłuższych przekątnych) lub z romboedr lub równoległościanu ( mniej symetryczne wielościany, które nadal mają taką samą strukturę kombinatoryczną jak sześcian). W przypadku sześcianu lub trójkąta trapezowego, w którym dwa ścięte wierzchołki są tymi na osiach rozciągania, wynikowy kształt ma potrójną symetrię obrotową .
Solid Dürera
Ten wielościan jest czasami nazywany bryłą Dürera , od jego pojawienia się w rycinie Albrechta Dürera z 1514 r. Melencolia I . Wykres utworzony przez jego krawędzie i wierzchołki nazywa się grafem Dürera .
Przedstawiony przez Dürera kształt bryły jest przedmiotem pewnej akademickiej debaty. Według Lyncha (1982) hipotezę, że kształt jest błędnie narysowanym ściętym sześcianem, promował Strauss (1972) ; jednak większość źródeł zgadza się, że jest to obcięcie rombohedronu . Pomimo tego porozumienia, dokładna geometria tego romboedru jest przedmiotem kilku sprzecznych teorii:
- Richter (1957) twierdzi, że romb, z którego uformowany jest ten kształt, ma stosunek ich krótkiej i długiej przekątnej 5:6, od którego kąty ostre rombów wynosiłyby około 80°.
- Schröder (1980) i Lynch (1982) zamiast tego wnioskują, że stosunek wynosi √3:2 i że kąt wynosi około 82°.
- MacGillavry (1981) mierzy cechy rysunku i stwierdza, że kąt wynosi około 79°. Ona i późniejszy autor, Wolf von Engelhardt (patrz Hideko 2009 ) twierdzą, że ten wybór kąta wynika z jego fizycznego występowania w kryształach kalcytu .
- Schreiber (1999) twierdzi na podstawie pism Dürera, że wszystkie wierzchołki bryły Dürera leżą na wspólnej sferze, a ponadto twierdzi, że kąty rombu wynoszą 72°. Hideko (2009) wymienia kilku innych badaczy, którzy również popierają teorię 72°, poczynając od Paula Grodzińskiego w 1955. Twierdzi on, że teoria ta jest motywowana w mniejszym stopniu analizą samego rysunku, a bardziej zasadami estetycznymi odnoszącymi się do pięciokątów foremnych i złotego stosunek .
- Weitzel (2004) analizuje szkic Dürera z 1510 r. o tej samej bryle, na podstawie którego potwierdza hipotezę Schreibera, że kształt ma okrąg okrężny, ale z kątami rombowymi wynoszącymi około 79,5°.
- Hideko (2009) twierdzi, że kształt ma przedstawiać rozwiązanie słynnego geometrycznego problemu podwojenia sześcianu , o którym Dürer również pisał w 1525 roku. Stwierdza zatem, że (przed odcięciem rogów) kształt jest rozciągniętym sześcianem wzdłuż jego długiej przekątnej. Mówiąc dokładniej, twierdzi, że Dürer narysował rzeczywisty sześcian z długą przekątną równoległą do płaszczyzny perspektywy , a następnie powiększył swój rysunek o pewien współczynnik w kierunku długiej przekątnej; wynik byłby taki sam, jak gdyby narysował wydłużoną bryłę. Współczynnik powiększenia, który jest istotny dla podwojenia sześcianu, wynosi 2 1/3 ≈ 1,253, ale Hideko wyprowadza inny współczynnik powiększenia, który lepiej pasuje do rysunku, 1,277, w bardziej skomplikowany sposób.
- Futamura, Frantz i Crannell (2014) klasyfikują proponowane rozwiązania tego problemu według dwóch parametrów: kąta ostrego i poziomu cięcia, zwanego współczynnikiem krzyżowym. Ich oszacowanie współczynnika krzyżowego jest zbliżone do MacGillavry'ego i ma wartość liczbową zbliżoną do złotego podziału . Na tej podstawie zakładają, że kąt ostry jest równy, a stosunek krzyżowy jest dokładnie równy .
Zobacz też
- Sfazowany czworościan , inny kształt utworzony przez obcięcie podzbioru wierzchołków sześcianu
Uwagi
Bibliografia
- Lynch, Terence (1982), „Geometryczne ciało w grawerowaniu Dürera Melencolia I ”, Journal of the Warburg and Courtauld Institutes , The Warburg Institute, 45 : 226-232, doi : 10.2307/750979 , JSTOR 750979.
- MacGillavry, C. (1981), „Wielościan w A. Dürers Melencolia I”, Nederl. Akad. Wetenscha. Proc. Ser. B , 84 : 287–294. Cytowane Weitzel (2004) .
- Richter, DH (1957), "Perspektive und Proportionen w Albrechta Dürers "Melancholie " ", Z. Vermessungswesen , 82 : 284-288 i 350-357. Cytowane Weitzel (2004) .
- Schreiber, Peter (1999), "Nowa hipoteza o enigmatycznym wielościanu Dürera w jego miedzi grawerowanie "melancholia i " " Historia Mathematica , 26 (4): 369-377, doi : 10,1006 / hmat.1999.2245.
- Schröder, E. (1980), Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner "Underweysung" , Bazylea. Cytowane Weitzel (2004) .
- Strauss, Walter L. (1972), The Complete Engravings of Dürer , New York, s. 168, ISBN 0-486-22851-7. Cyt. Lynch (1982) .
- Weber, P. (1900), Beiträge zu Dürers Weltanschauung – Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus , Strassburg. Cytowane Weitzel (2004) .
- Weitzel, Hans (2004), „Kolejna hipoteza na wielościan grawerowania A. Dürera Melencolia I”, Historia Mathematica , 31 (1): 11-14, doi : 10.1016/S0315-0860 (03) 00029-6.
- Hideko, Ishizu (2009), „Inne rozwiązanie wielościanu w Melencolia Dürera : Wizualna demonstracja problemu Delian” (PDF) , Estetyka , Japońskie Towarzystwo Estetyczne, 13 : 179-194.
- Ziegler, Günter M. (3 grudnia 2014), „Wielościan Dürera: 5 teorii wyjaśniających szaloną kostkę Melencolii” , Przygody Alexa Bellosa w Numberland, The Guardian.
- Futamura, F.; Frantz, M.; Crannell, A. (2014), „Stosunek krzyża jako parametr kształtu bryły Dürera”, Journal of Mathematics and the Arts , 8 (3-4): 111-119, arXiv : 1405.6481 , doi : 10.1080/17513472.2014.974483 , S2CID 120958490.



