Pierścień przemienny - Commutative ring

W teorii pierścieni , gałęzi algebry abstrakcyjnej , pierścień przemienny to pierścień, w którym operacja mnożenia jest przemienna . Badanie pierścieni przemiennych nazywa się algebrą przemienną . Uzupełniająco, algebra nieprzemienna to badanie nieprzemiennych pierścieni, w których mnożenie nie jest wymagane, aby było przemienne.

Definicja i pierwsze przykłady

Definicja

Pierścień jest Zestaw wyposażony jest w dwa operacji binarnych , czyli operacje łączące dwa dowolne elementy pierścienia, do jednej trzeciej. Nazywa się je dodawaniem i mnożeniem i zwykle oznacza się je „ ” i „ ”; np . i . Aby utworzyć pierścień, te dwie operacje muszą spełniać szereg właściwości: pierścień musi być grupą abelową podczas dodawania, a także monoidem podczas mnożenia, gdzie mnożenie jest rozłożone na dodawanie; tj . Elementy identyfikacyjne dla dodawania i mnożenia są oznaczone i , odpowiednio. ${\ displaystyle R}$ ${\ displaystyle +}$ ${\ displaystyle \ cdot}$ ${\ displaystyle a + b}$ ${\ displaystyle a \ cdot b}$ ${\ Displaystyle a \ cdot \ lewo (b + c \ prawo) = \ lewo (a \ cdot b \ prawo) + \ lewo (a \ cdot c \ prawo)}$ ${\ displaystyle 0}$ ${\ displaystyle 1}$

Jeśli mnożenie jest przemienne, tj

{\ Displaystyle a \ cdot b = b \ cdot a,}

wtedy pierścień nazywa się przemiennym . W pozostałej części tego artykułu wszystkie pierścienie będą przemienne, chyba że wyraźnie zaznaczono inaczej. ${\ displaystyle R}$

Pierwsze przykłady

Ważnym przykładem, w pewnym sensie kluczowym, jest pierścień liczb całkowitych z dwiema operacjami dodawania i mnożenia. Ponieważ mnożenie liczb całkowitych jest operacją przemienną, jest to pierścień przemienny. Zwykle jest oznaczany jako skrót od

niemieckiego słowa Zahlen (liczby).

{\ displaystyle \ mathbb {Z}}

${\ displaystyle \ mathbb {Z}}$

Pole jest przemienne w pierścieniu, gdzie a każdy

niezerowy elementem jest odwracalna; tj. ma multiplikatywną odwrotność taką, że . Dlatego z definicji każde pole jest pierścieniem przemiennym. Te racjonalne , realne i liczby zespolone tworzą pola.

{\ Displaystyle 0 \ nie = 1}

{\ displaystyle a}

{\ displaystyle b}

{\ Displaystyle a \ cdot b = 1}

Jeśli jest danym pierścieniem przemiennym, to zbiór wszystkich

wielomianów w zmiennej, której współczynniki są w, tworzy pierścień wielomianowy , oznaczony . To samo dotyczy kilku zmiennych. ${\ displaystyle R}$

{\ displaystyle X}

${\ displaystyle R}$

{\ Displaystyle R \ lewo [X \ prawo]}

Jeśli jest jakaś

przestrzeń topologiczna , na przykład podzbiór niektórych funkcji ciągłych o wartościach rzeczywistych lub zespolonych w postaci pierścienia przemiennego. To samo jest prawdziwe dla różniczkowalnych lub holomorficznymi funkcji , kiedy dwa pojęcia są zdefiniowane, takich jak w złożonych kolektora . ${\ displaystyle V}$

{\ displaystyle \ mathbb {R} ^ {n}}

${\ displaystyle V}$ ${\ displaystyle V}$

Podzielność

W przeciwieństwie do pól, w których każdy element niezerowy jest multiplikatywnie odwracalny, pojęcie podzielności dla pierścieni jest bogatsze. Element pierścienia nazywany jest

jednostką, jeśli posiada multiplikatywną odwrotność. Innym szczególnym rodzajem elementu są dzielniki zerowe , tj. Element taki, że istnieje niezerowy element pierścienia taki, że . Jeśli nie ma niezerowych dzielników zerowych, nazywa się to domeną całkową (lub domeną). Element spełniający wymagania dla pewnej dodatniej liczby całkowitej nazywa się nilpotent .

{\ displaystyle a}

${\ displaystyle R}$

{\ displaystyle a}

{\ displaystyle b}

{\ displaystyle ab = 0}

${\ displaystyle R}$

{\ displaystyle a}

{\ displaystyle a ^ {n} = 0}

{\ displaystyle n}

Lokalizacje

Lokalizacja pierścienia jest procesem, w której niektóre elementy są renderowane odwracalny, tj multiplikatywne odwrotności dodaje się do pierścienia. Konkretnie, jeżeli jest

multiplikatywnie zamknięty podzbiór z (to znaczy, gdy następnie tak samo ), to lokalizacja stanowi na lub pierścień z frakcji z mianownik , zazwyczaj oznaczone składa się z symboli ${\ displaystyle S}$ ${\ displaystyle R}$

{\ Displaystyle s, t \ w S}

{\ displaystyle st}

${\ displaystyle R}$ ${\ displaystyle S}$ ${\ displaystyle S}$

{\ Displaystyle S ^ {- 1} R}

{\ displaystyle {\ frac {r} {s}}}

z

{\ Displaystyle r \ w R, s \ w S}

podlega pewnym regułom, które naśladują anulowanie znane z liczb wymiernych. Rzeczywiście, w tym języku jest lokalizacja wszystkich niezerowych liczb całkowitych. Ta konstrukcja działa dla dowolnej domeny integralnej zamiast . Umiejscowienie to pole, zwane

pole iloraz z . ${\ displaystyle \ mathbb {Q}}$ ${\ displaystyle \ mathbb {Z}}$ ${\ displaystyle R}$ ${\ displaystyle \ mathbb {Z}}$

{\ Displaystyle \ lewo (R \ ukośnik odwrotny \ lewo \ {0 \ prawo \} \ prawo) ^ {- 1} R}

${\ displaystyle R}$

Ideały i moduły

Istnieje również wiele z poniższych pojęć dotyczących pierścieni niekoniecznie przemiennych, ale definicje i właściwości są zwykle bardziej skomplikowane. Na przykład wszystkie ideały w pierścieniu przemiennym są automatycznie dwustronne , co znacznie upraszcza sytuację.

Moduły i ideały

Na pierścieniu , -

moduł jest jak co przestrzeni wektorowej jest polem. Oznacza to, że można dodawać elementy w module; można je pomnożyć przez elementy podmiotu podlegającego tym samym aksjomatom, jak dla przestrzeni wektorowej. Badanie modułów jest znacznie bardziej zaangażowane niż badanie przestrzeni wektorowych w algebrze liniowej , ponieważ kilka cech przestrzeni wektorowych zawodzi dla modułów w ogóle: moduły nie muszą być wolne , tj. ${\ displaystyle R}$ ${\ displaystyle R}$ ${\ displaystyle M}$ ${\ displaystyle R}$

{\ Displaystyle M = \ bigoplus _ {ja \ w I} R.}

Nawet w przypadku wolnych modułów ranga wolnego modułu (tj. Odpowiednik wymiaru przestrzeni wektorowej) może nie być dobrze zdefiniowana. Wreszcie, podmoduły nieskończenie generowanych modułów nie muszą być generowane w sposób skończony (chyba że jest Noetherian, patrz poniżej ). ${\ displaystyle R}$

Ideały

Idee w pierścieniu są

podmoduły z , to jest zawarty w moduły . Bardziej szczegółowo, idealna jest niepusty podzbiór taki sposób, aby dla wszystkich IN , i w zarówno i są . W przypadku różnych zastosowań zrozumienie ideałów pierścienia ma szczególne znaczenie, ale często kontynuuje się studiowanie ogólnie modułów. ${\ displaystyle R}$ ${\ displaystyle R}$ ${\ displaystyle R}$ ${\ displaystyle I}$ ${\ displaystyle R}$ ${\ displaystyle r}$ ${\ displaystyle R}$ ${\ displaystyle i}$ ${\ displaystyle j}$ ${\ displaystyle I}$ ${\ displaystyle ri}$ ${\ displaystyle i + j}$ ${\ displaystyle I}$

Każdy pierścień ma dwa ideały, a mianowicie ideał zerowy i cały pierścień. Te dwa ideały są jedynymi dokładnie, jeśli jest polem. Biorąc pod uwagę dowolny podzbiór o (gdzie pewien zestaw index), idealny

generowane przez to najmniejsza idealnym, który zawiera . Równoważnie, jest on określony przez skończone kombinacje liniowe ${\ Displaystyle \ lewo \ {0 \ prawo \}}$ ${\ displaystyle R}$ ${\ displaystyle R}$ ${\ displaystyle F = \ lewo \ {f_ {j} \ prawo \} _ {j \ w J}}$ ${\ displaystyle R}$ ${\ displaystyle J}$ ${\ displaystyle F}$ ${\ displaystyle F}$

{\ Displaystyle r_ {1} f_ {1} + r_ {2} f_ {2} + \ kropki + r_ {n} f_ {n}.}

Główne domeny idealne

Jeśli składa się z pojedynczego elementu , to ideał generowany przez składa się z wielokrotności , czyli elementów formy dla dowolnych elementów . Taki ideał nazywa się ideałem głównym . Jeśli każdy ideał jest ideałem głównym, nazywany jest pierścieniem ideału głównego ; dwa ważne przypadki to i , wielomianowy pierścień na polu . Te dwie domeny są dodatkowymi domenami, więc nazywane są głównymi domenami idealnymi . ${\ displaystyle F}$ ${\ displaystyle r}$ ${\ displaystyle F}$ ${\ displaystyle r}$ ${\ displaystyle rs}$ ${\ displaystyle s}$ ${\ displaystyle R}$ ${\ displaystyle \ mathbb {Z}}$ ${\ Displaystyle k \ lewo [X \ w prawo]}$ ${\ displaystyle k}$

W przeciwieństwie do pierścieni ogólnych, dla domeny idealnej głównej, właściwości poszczególnych elementów są silnie powiązane z właściwościami pierścienia jako całości. Na przykład, każda główna domena idealna jest unikalną domeną faktoryzacji (UFD), co oznacza, że każdy element jest produktem elementów nieredukowalnych w unikalny sposób (aż do zmiany kolejności czynników). Tutaj element a w domenie nazywany jest nieredukowalnym, jeśli jest to jedyny sposób wyrażenia go jako produktu ${\ displaystyle R}$

{\ displaystyle a = pne,}

jest albo czy jest jednostką. Przykładem, ważnym w teorii pola , są nieredukowalne wielomiany , tj. Nieredukowalne elementy w , dla pola . Fakt, że jest to UFD, można stwierdzić bardziej elementarnie, mówiąc, że każda liczba naturalna może być jednoznacznie rozłożona jako iloczyn potęg liczb pierwszych. Jest również znany jako podstawowe twierdzenie arytmetyki . ${\ displaystyle b}$ ${\ displaystyle c}$ ${\ Displaystyle k \ lewo [X \ w prawo]}$ ${\ displaystyle k}$ ${\ displaystyle \ mathbb {Z}}$

Element jest elementem

głównym, jeśli ilekroć dzieli produkt , dzieli lub . W domenie bycie pierwszym oznacza bycie nieredukowalnym. Odwrotna sytuacja jest prawdą w unikalnej dziedzinie faktoryzacji, ale ogólnie jest fałszywa. ${\ displaystyle a}$ ${\ displaystyle a}$ ${\ displaystyle bc}$ ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle c}$

Pierścień czynnikowy

Definicja idei jest taka, że „podział” „Z” daje inny pierścień z

pierścieniem czynnik / : to zestaw cosets z razem z operacjami ${\ displaystyle I}$ ${\ displaystyle R}$ ${\ displaystyle I}$ ${\ displaystyle I}$

{\ Displaystyle \ lewo (a + ja \ prawo) + \ lewo (b + ja \ prawo) = \ lewo (a + b \ prawo) + ja}

i . Na przykład pierścień (również oznaczony ), gdzie jest liczbą całkowitą, jest pierścieniem liczb całkowitych modulo . Jest podstawą arytmetyki modularnej . ${\ Displaystyle \ lewo (a + ja \ prawo) \ lewo (b + ja \ prawo) = ab + ja}$

{\ Displaystyle \ mathbb {Z} / n \ mathbb {Z}}

{\ displaystyle \ mathbb {Z} _ {n}}

${\ displaystyle n}$ ${\ displaystyle n}$

Ideał jest właściwy, jeśli jest ściśle mniejszy niż cały pierścionek. Ideał, który nie jest ściśle zawarty w żadnym odpowiednim ideale, nazywany jest maksymalnym . Ideał jest maksymalny

wtedy i tylko wtedy, gdy / jest polem. Z wyjątkiem pierścienia zerowego , każdy pierścień (z tożsamością) posiada przynajmniej jeden maksymalny ideał; wynika to z lematu Zorna . ${\ displaystyle m}$ ${\ displaystyle R}$ ${\ displaystyle m}$

Pierścienie Noetherian

Pierścień nazywa się Noetherian (na cześć Emmy Noether , która opracowała tę koncepcję), jeśli każdy rosnący łańcuch ideałów

{\ Displaystyle 0 \ subseteq I_ {0} \ subseteq I_ {1} \ subseteq \ kropki \ subseteq I_ {n} \ subseteq I_ {n + 1} \ kropki}

staje się nieruchomy, tj. staje się stały poza jakimś indeksem . Równoważnie, każdy ideał jest generowany przez skończenie wiele elementów lub, choć równoważne, submoduły skończenie generowanych modułów są generowane w sposób skończony. ${\ displaystyle n}$

Bycie Noetherianem jest bardzo ważnym warunkiem skończoności, a warunek ten jest zachowywany w przypadku wielu operacji, które często występują w geometrii. Na przykład, jeśli jest Noetherian, to tak samo jest z pierścieniem wielomianowym (według

twierdzenia Hilberta o podstawie ), dowolną lokalizacją , a także dowolnym pierścieniem czynnikowym / . ${\ displaystyle R}$ ${\ Displaystyle R \ lewo [X_ {1}, X_ {2}, \ kropki, X_ {n} \ w prawo]}$ ${\ Displaystyle S ^ {- 1} R}$ ${\ displaystyle R}$ ${\ displaystyle I}$

Każdy pierścień nie-noeterii jest

połączeniem jego podrzędnych pierścieni Noether. Fakt ten, znany jako aproksymacja Noetherian , pozwala na rozszerzenie pewnych twierdzeń na pierścienie inne niż Noetherian. ${\ displaystyle R}$

Pierścienie artyńskie

Pierścień nazywa się Artinian (od Emila Artina ), jeśli każdy zstępujący łańcuch ideałów

{\ Displaystyle R \ supseteq I_ {0} \ supseteq I_ {1} \ supseteq \ kropki \ supseteq I_ {n} \ supseteq I_ {n + 1} \ kropki}

w końcu staje się nieruchoma. Pomimo dwóch warunków, które wydają się symetryczne, pierścienie Noeterii są znacznie bardziej ogólne niż pierścienie Artynii. Na przykład jest Noetherian, ponieważ każdy ideał może zostać wygenerowany przez jeden element, ale nie jest Artynem, ponieważ łańcuch ${\ displaystyle \ mathbb {Z}}$ ${\ Displaystyle \ mathbb {Z} \ supsetneq 2 \ mathbb {Z} \ supsetneq 4 \ mathbb {Z} \ supsetneq 8 \ mathbb {Z} \ kropki}$ przedstawia. W rzeczywistości, zgodnie z twierdzeniem Hopkinsa – Levitzkiego , każdy pierścień artyński jest Noetherian. Dokładniej, pierścienie artynińskie można scharakteryzować jako pierścienie Noeterii, których wymiar Krulla wynosi zero.

Widmo pierścienia przemiennego

Pierwotne ideały

Jak wspomniano powyżej, jest to

wyjątkowa dziedzina faktoryzacji . Nie dotyczy to bardziej ogólnych pierścieni, jak zdali sobie sprawę algebraicy w XIX wieku. Na przykład w ${\ displaystyle \ mathbb {Z}}$

{\ Displaystyle \ mathbb {Z} \ lewo [{\ sqrt {-5}} \ prawo]}

istnieją dwa naprawdę różne sposoby zapisania 6 jako produktu:

{\ Displaystyle 6 = 2 \ cdot 3 = \ lewo (1 + {\ sqrt {-5}} \ prawo) \ lewo (1 - {\ sqrt {-5}} \ po prawej).}

Pierwotne ideały, w przeciwieństwie do pierwiastków pierwszych, stanowią sposób na obejście tego problemu. Ideał pierwszy jest właściwym (tj. Ściśle zawartym w ) ideałem takim, że ilekroć iloczyn dowolnych dwóch elementów pierścienia i jest w środku, co najmniej jeden z dwóch elementów już się znajduje . (Odwrotny wniosek dotyczy każdego ideału, z definicji). Tak więc, jeśli ideał pierwszy jest główny, to jest on równoważnie generowany przez element pierwszy. Jednak w pierścieniach takich jak pierwszorzędne ideały nie muszą być głównymi. Ogranicza to użycie pierwiastków pierwszych w teorii pierścieni. Kamieniem węgielnym algebraicznej teorii liczb jest jednak fakt, że w każdym pierścieniu Dedekinda (który obejmuje i bardziej ogólnie pierścień liczb całkowitych w polu liczbowym ) każdy ideał (taki jak ten generowany przez 6) rozkłada się jako iloczyn liczby pierwszej ideały. ${\ displaystyle R}$ ${\ displaystyle p}$ ${\ displaystyle ab}$ ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle p}$ ${\ displaystyle p}$

{\ Displaystyle \ mathbb {Z} \ lewo [{\ sqrt {-5}} \ prawo]}

{\ Displaystyle \ mathbb {Z} \ lewo [{\ sqrt {-5}} \ prawo]}

Każdy ideał maksymalny jest ideałem pierwszym lub, mówiąc w skrócie, jest pierwszym. Co więcej, ideał jest pierwszy wtedy i tylko wtedy, gdy czynnik pierścienia / jest dziedziną całkową. Udowodnienie, że ideał jest liczbą pierwszą lub równoważnie, że pierścień nie ma zerowych dzielników, może być bardzo trudne. Jeszcze innym sposobem wyrażenia tego samego jest stwierdzenie, że

dopełnienie jest zwielokrotnione. Lokalizację ( R \ p ) ^-1R ma znaczenie wystarczy mieć własną oznaczenia: . Ten pierścień ma tylko jeden maksymalny ideał, a mianowicie . Takie pierścienie nazywane są lokalnymi . ${\ displaystyle I}$ ${\ displaystyle R}$ ${\ displaystyle I}$ ${\ displaystyle R \ backslash p}$ ${\ Displaystyle \ lewo (R \ ukośnik odwrotny p \ w prawo) ^ {- 1} R}$ ${\ displaystyle R_ {p}}$ ${\ displaystyle pR_ {p}}$

Widmo

Spec ( Z ) zawiera punkt dla ideału zerowego. Zamknięciem tego punktu jest cała przestrzeń. Pozostałe punkty to punkty odpowiadające ideałom ( p ), gdzie p jest liczbą pierwszą. Te punkty są zamknięte.

Spektrum pierścienia ${\ displaystyle R}$ , oznaczony jest zbiorem wszystkich głównych idei . Jest wyposażony w topologię, topologię

Zariskiego , która odzwierciedla algebraiczne własności : podstawa podzbiorów otwartych jest ${\ displaystyle {\ text {Spec}} \ R}$ ${\ displaystyle R}$ ${\ displaystyle R}$

{\ Displaystyle D \ lewo (fa \ prawo) = \ lewo \ {p \ w {\ tekst {Spec}} \ R, f \ nie \ w p \ w prawo \}}

, gdzie jest jakikolwiek element pierścienia. Interpretując jako funkcję, która przyjmuje wartość f mod p (tj. Obraz f w polu reszt R / p ), podzbiór ten jest miejscem, w którym f jest niezerowe. Widmo precyzuje również intuicję, że pierścienie lokalizacyjne i czynnikowe są komplementarne: mapy naturalne R → R _f i R → R / fR odpowiadają, po wyposażeniu widm tych pierścieni w ich topologię Zariski, komplementarnym zanurzeniom otwartym i zamkniętym odpowiednio. Nawet w przypadku pierścieni podstawowych, takich jak zilustrowane dla R = Z po prawej stronie, topologia Zariski jest zupełnie inna niż w przypadku zbioru liczb rzeczywistych. ${\ displaystyle f}$ ${\ displaystyle f}$

Widmo zawiera zbiór maksymalnych ideałów, czasami oznaczany jako mSpec ( R ). Dla algebraicznie zamkniętego pola k , mSpec (k [ T ₁ , ..., T _n ] / ( f ₁ , ..., f _m )) jest w układzie bijekcyjnym ze zbiorem

{ x = ( x ₁ , ..., x _n ) ∊ k ⁿ

Zatem ideały maksymalne odzwierciedlają właściwości geometryczne zbiorów rozwiązań wielomianów, co jest początkową motywacją do badania pierścieni przemiennych. Jednak uwzględnienie nie-maksymalnych ideałów jako części geometrycznych właściwości pierścienia jest przydatne z kilku powodów. Na przykład, minimalna ideał pierwszy (to znaczy te, które nie są ściśle zawierające mniejsze) są zgodne z nieredukowalnych składników spec R . Jak na pierścień Noetherian R , Spec R ma tylko skończenie wiele nieredukowalnych składników. Jest to geometryczne przekształcenie pierwotnego rozkładu , zgodnie z którym każdy ideał może zostać rozłożony jako produkt nieskończenie wielu pierwotnych ideałów . Fakt ten jest ostatecznym uogólnieniem rozkładu na pierwszorzędne ideały pierścieni Dedekinda.

Schematy afiniczne

Pojęcie widma jest wspólną podstawą algebry przemiennej i geometrii algebraicznej . Algebraiczne przebiega przez geometryczną nadając Spec R w wiązce (podmiot, który działa zbiera określonego lokalnie, to znaczy w różnych podzbiorów otwartych). Punkt odniesienia przestrzeni i snopa nazywa się

schematem afinicznym . Biorąc afinicznych systemu, podstawowe koło R można odzyskać jako globalne sekcje o . Co więcej, ta zgodność jeden do jednego między pierścieniami i schematami afinicznymi jest również zgodna z homomorfizmami pierścieni: każde f : R → S daje początek ciągłej mapie w przeciwnym kierunku

{\ displaystyle {\ mathcal {O}}}

{\ displaystyle {\ mathcal {O}}}

Widmo S → Widmo R , Q ↦ f ^-1 ( Q ), to jakiekolwiek ideałem z S są odwzorowywane na jego preimage pod F , który jest głównym ideał R .

Wynikająca z tego równoważność obu wymienionych kategorii trafnie odzwierciedla algebraiczne właściwości pierścieni w sposób geometryczny.

Podobnie jak to, że rozmaitości są lokalnie podawane przez podzbiory otwarte R ⁿ , schematy afiniczne są lokalnymi modelami schematów , które są przedmiotem badań geometrii algebraicznej. Dlatego kilka pojęć dotyczących pierścieni przemiennych wywodzi się z intuicji geometrycznej.

Wymiar

Wymiar Krull (albo wymiar) Dim R pierścienia R środków, „wielkość” w pierścieniu, z grubsza rzecz biorąc, licząc niezależnych elementów R . Wymiar algebr nad ciałem k można zaksjomatyzować czterema właściwościami:

Wymiar jest lokalną własnością: wym R = sup _{p ∊ Spec R} dim R _p .
Wymiar ten zależy od elementów nilpotent: Jeśli mi ⊆ R jest nilpotent następnie słabe R = słabe R / I .
Wymiar pozostaje stały przy skończonej rozszerzenia: jeżeli S jest R -algebra który skończenie generowane jako R -module, po czym ciemny S = słabe R .
Wymiar jest kalibrowany przez dim k [ X ₁ , ..., X _n ] = n . Ten aksjomat jest motywowany traktowaniem pierścienia wielomianu w n zmiennych jako algebraicznego odpowiednika przestrzeni n- wymiarowej .

Wymiar jest zdefiniowany dla dowolnego pierścienia R jako supremum długości n łańcuchów ideałów pierwszych

p ₀ ⊊ p ₁ ⊊ ... ⊊ p _n .

Na przykład pole jest zerowymiarowe, ponieważ jedynym pierwszym ideałem jest ideał zerowy. Liczby całkowite są jednowymiarowe, ponieważ łańcuchy mają postać (0) ⊊ ( p ), gdzie p jest liczbą pierwszą . W przypadku pierścieni innych niż Noetherian, a także pierścieni nielokalnych, wymiar może być nieskończony, ale lokalne pierścienie Noether mają wymiar skończony. Wśród czterech aksjomatów powyżej, pierwsze dwa są elementarne konsekwencje definicji, natomiast pozostałe dwa zawiasy na ważnych faktów w przemiennej algebry The dzieje się twierdzenie i ideał główny twierdzenie krulla .

Homomorfizmy pierścieniowe

Homomorfizm pierścień lub, potocznie prostu mapa jest mapa F : R → S tak, że

f ( a + b ) = f ( a ) + f ( b ), f ( ab ) = f ( a ) f ( b ) if (1) = 1.

Warunki te zapewniają f (0) = 0. Podobnie jak w przypadku innych struktur algebraicznych, homomorfizm pierścieniowy jest więc mapą zgodną ze strukturą omawianych obiektów algebraicznych. W takiej sytuacji S jest również nazywany R -algebrą, rozumiejąc, że s w S można pomnożyć przez pewne r z R , ustawiając

r · s : = f ( r ) · s .

Jądra i obrazu z f jest określony przez ker ( f ) = { R ∈ R , f ( R ) = 0} i IM ( f ) = C ( R ) = { f ( R ) R ∈ R }. Jądro jest idealny z R , a obraz jest podpierścień z S .

Homomorfizm pierścieniowy nazywany jest izomorfizmem, jeśli jest bijektywny. Przykładem izomorfizmu pierścienia, znanego jako chińskie twierdzenie o resztach , jest

{\ Displaystyle \ mathbf {Z} / n = \ bigoplus _ {i = 0} ^ {k} \ mathbf {Z} / p_ {i}}

gdzie n = p ₁ p ₂ ... p _k jest iloczynem parami różnych liczb pierwszych .

Pierścienie przemienne, wraz z homomorfizmami pierścieni, tworzą kategorię . Pierścień Z jest początkowy przedmiot w tej kategorii, co oznacza, że dla każdej przemiennej pierścienia R , jest unikalny pierścień homomorfizm Z → R . Za pomocą tej mapie liczba całkowita n mogą być traktowane jako element B . Na przykład wzór dwumianowy

{\ Displaystyle (a + b) ^ {n} = \ suma _ {k = 0} ^ {n} {\ binom {n} {k}} a ^ {k} b ^ {nk}}

który jest ważny dla dowolnych dwóch elementów a i b w dowolnym pierścieniu przemiennym R jest rozumiany w tym sensie przez interpretację współczynników dwumianowych jako elementów R przy użyciu tej mapy.

Uniwersalną właściwością od S ⊗ _R T twierdzi, że dla każdego dwie mapy S → W i T → W , które sprawiają, że zewnętrzny czworokąt dojazdy, istnieje unikalna mapa S ⊗ _R T → W , który sprawia, że cały schemat dojazdy.

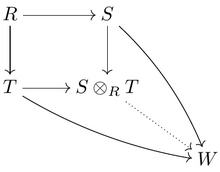
Biorąc pod uwagę dwie R -algebry S i T , ich iloczyn tensorowy

S ⊗ _R T.

jest ponownie przemienną R -algebrą. W pewnych przypadkach, produkt może służyć tensora znaleźć T -algebrze który odnosi się do Z, a S odnosi się do badania . Na przykład,

R [ X ] ⊗ _R T = T [ X ].

Skończone pokolenie

R -algebra S nazywany jest skończoną generowane (jako Algebra) , jeśli nie są skończenie wiele elementów s ₁ , ..., y _n , takich, że każdy element s jest do ekspresji jako wielomian w y _{: i} . Równoważnie S jest izomorficzna z

R [ T ₁ , ..., T _n ] / I .

Znacznie silniejszym warunkiem jest to, że S jest generowane w sposób skończony jako R -moduł , co oznacza, że dowolne s można wyrazić jako R- liniową kombinację pewnego skończonego zbioru s ₁ , ..., s _n .

Lokalne pierścienie

Pierścień nazywany jest lokalnym, jeśli ma tylko jeden ideał maksymalny, oznaczony przez m . Dla każdego (niekoniecznie lokalnego) w pierścieniu B , lokalizacji

R _p

w najlepszym przypadku idealna p jest lokalna. Ta lokalizacja odzwierciedla geometryczne właściwości Spec R „wokół p ”. Kilka pojęć i problemów w algebrze przemiennej można sprowadzić do przypadku, gdy R jest lokalna, czyniąc pierścienie lokalne szczególnie głęboko zbadaną klasą pierścieni. Pole pozostałość z R jest zdefiniowany jako

k = R / m .

Każdy moduł R M daje przestrzeń k- wektorową określoną przez M / mM . Lemat Nakayamy pokazuje, że ten fragment zachowuje ważne informacje: skończenie generowany moduł M wynosi zero wtedy i tylko wtedy, gdy M / mM wynosi zero.

Regularne pierścienie lokalne

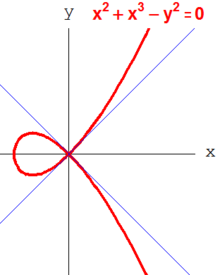
Sześcienny płaszczyzny krzywą (kolor czerwony), określonej przez równanie: r ² = x ² ( x + 1 ) stanowi pojedynczą na początku, to znaczy pierścień K [ x , y ] / r ² - x ² ( x + 1 ) jest nie zwykły pierścionek. Stożek (niebieski) jest połączeniem dwóch linii, co również odzwierciedla osobliwość.

Przestrzeń wektorowa k m / m ² jest algebraicznym wcieleniem przestrzeni cotangens . Nieformalnie, elementy m można traktować jako funkcje, które znikają w punkcie p , podczas gdy m ² zawiera te, które znikają z kolejnością co najmniej 2. Dla dowolnego noetherowskiego pierścienia lokalnego R nierówność

wym _k m / m ² ≥ wym R

Odnosi się to, co świadczy o koncepcję, że cotangent (lub równoważnie styczna) przestrzeń ma co najmniej wymiar przestrzeni Spec R . Jeśli równość jest prawdziwa w tym oszacowaniu, R nazywa się zwykłym pierścieniem lokalnym . Noetherian lokalny pierścień jest regularny wtedy i tylko wtedy, gdy pierścień (który jest pierścieniem funkcji na stożku stycznym )

{\ Displaystyle \ bigoplus _ {n} m ^ {n} / m ^ {n + 1}}

jest izomorficzny do wielomianowego pierścienia nad k . Mówiąc ogólnie, regularne pierścienie lokalne są nieco podobne do pierścieni wielomianowych. Regularne lokalne pierścienie to UFD.

Dyskretne pierścienie wyceny wyposażone są w funkcję przypisującą liczbę całkowitą do dowolnego elementu r . Liczbę tę, nazywaną wartością r, można nieformalnie traktować jako zero lub rząd biegunów r . Dyskretne pierścienie wyceny to właśnie jednowymiarowe regularne pierścienie lokalne. Na przykład pierścień zarodków funkcji holomorficznych na powierzchni Riemanna jest dyskretnym pierścieniem wartościującym.

Pełne skrzyżowania

Skręcone sześcienny (zielony) jest kompletny zestaw-teoretyczny punkt przecięcia, nie pełne przecięcie.

Zgodnie z głównym ideałem twierdzenia Krulla, podstawowy wynik w teorii wymiarów pierścieni , wymiar

R = k [ T ₁ , ..., T _r ] / ( f ₁ , ..., f _n )

jest co najmniej r - n . Pierścień R nazywany jest kompletnym pierścieniem przecięcia, jeśli można go przedstawić w sposób, który osiąga tę minimalną granicę. Pojęcie to jest również najczęściej badane w przypadku pierścieni lokalnych. Każdy regularny pierścień lokalny jest kompletnym pierścieniem przecinającym, ale nie odwrotnie.

Pierścień R jest całkowitym przecięciem według teorii mnogości, jeśli zredukowany pierścień związany z R , tj. Ten otrzymany przez podzielenie wszystkich elementów zerowych, jest całkowitym przecięciem. Od 2017 r. Na ogół nie wiadomo, czy krzywe w przestrzeni trójwymiarowej są kompletnymi skrzyżowaniami opartymi na teorii zbiorów.

Pierścienie Cohena-Macaulaya

Głębokość miejscowego pierścienia R jest liczbą elementów na niektórych (lub, jak to pokazano, każdy) maksymalnej określonej sekwencji, czyli sekwencję

₁ , ..., _n ∈ M tak, że wszystkie _i nie podlegają -zero dzielników w

R / ( a ₁ , ..., a _{i −1} ).

Nierówność dla każdego lokalnego pierścienia Noetherian

głębokość ( R ) ≤ dim ( R )

trzyma. Lokalny pierścień, w którym ma miejsce równość, nazywany jest pierścieniem Cohena-Macaulaya . Lokalne kompletne pierścienie przecięcia i a fortiori, regularne lokalne pierścienie to Cohen – Macaulay, ale nie odwrotnie. Cohen – Macaulay łączą pożądane właściwości regularnych pierścieni (takie jak właściwość bycia uniwersalnymi pierścieniami łańcuchowymi , co oznacza, że (co) wymiar liczb pierwszych jest dobrze zachowany), ale są też bardziej wytrzymałe przy obliczaniu ilorazów niż zwykłe pierścienie lokalne.

Konstruowanie pierścieni przemiennych

Istnieje kilka sposobów na zbudowanie nowych pierścieni z podanych. Celem takich konstrukcji jest często polepszenie pewnych właściwości pierścienia, aby uczynić go bardziej zrozumiałym. Na przykład całka domena, która jest integralnie zamknięta w swoim polu ułamków, nazywana jest normalną . Jest to pożądana właściwość, na przykład każdy normalny jednowymiarowy pierścień jest z konieczności regularny . Renderowanie normalnego pierścienia jest znane jako normalizacja .

Ukończenia

Jeśli że jest idealnym w przemiennej pierścienia R , uprawnienia I tworzą topologiczne sąsiedztwa z 0 pozwalające R należy traktować jako pierścień topologicznych . Ta topologia jest nazywana

topologią I -adic . R można następnie uzupełnić w odniesieniu do tej topologii. Formalnie I -adyczne uzupełnienie jest odwrotną granicą pierścieni R / I ⁿ . Na przykład, jeśli k jest pole, k [[ X ]] The formalne szereg potęgowy pierścień jednej zmiennej na k , jest to , że -adic zakończenie k [ X ] gdzie I jest głównym idealnym generowane przez X . Ten pierścień służy jako algebraiczny odpowiednik dysku. Analogicznie, pierścień p -adycznych liczb całkowitych jest uzupełnieniem Z względem ideału głównego ( p ). Każdy pierścień, który jest całkowicie izomorficzny, nazywany jest kompletnym .

Kompletny okolicy pierścieni spełniałby lemat Hensel użytkownika , co z grubsza umożliwia rozszerzenie rozwiązań (z różnymi problemami) do pozostałości pola K do badań .

Pojęcia homologiczne

Kilka głębszych aspektów pierścieni przemiennych zostało zbadanych przy użyciu metod z algebry homologicznej . Hochster (2007) wymienia kilka otwartych pytań w tym obszarze aktywnych badań.

Moduły rzutowe i funktory Ext

Moduły rzutowe można zdefiniować jako bezpośrednie sumy wolnych modułów. Jeśli R jest lokalny, każdy skończony moduł rzutowy jest w rzeczywistości wolny, co daje analogię między modułami rzutującymi i wiązkami wektorów . Twierdzenie Quillena – Suslina stwierdza, że każdy skończenie wygenerowany moduł rzutowy nad k [ T ₁ , ..., T _n ] ( k a ciałem) jest wolny, ale ogólnie te dwa pojęcia różnią się. Lokalny pierścień Noetherian jest regularny wtedy i tylko wtedy, gdy jego wymiar globalny jest skończony, powiedzmy n , co oznacza, że każdy skończony R- moduł ma rozdzielczość przez moduły projekcyjne o długości co najwyżej n .

Dowód na to i inne powiązane stwierdzenia opiera się na zastosowaniu metod homologicznych, takich jak funktor Ext . Funktor ten jest funktorem pochodnym funktora

Hom _R ( M , -).

Ten ostatni funktor jest dokładna, jeśli M jest rzutowe, ale nie inaczej: dla suriekcją mapie E → F z R -modules, mapa M → K nie musi rozciągać się do mapy M → E . Wyższe funktory Ext mierzą niedokładność funktora Homa. Znaczenie tej standardowej konstrukcji w algebrze homologicznej wynika z faktu, że lokalny pierścień Noetherian R z polem reszt k jest regularny wtedy i tylko wtedy, gdy

Ext ⁿ ( k , k )

znika dla wszystkich wystarczająco dużych n . Co więcej, wymiary tych grup Ext, znanych jako liczby Bettiego , rosną wielomianowo w n wtedy i tylko wtedy, gdy R jest lokalnym kompletnym pierścieniem

przecinającym . Kluczowym argumentem w takich rozważaniach jest kompleks Koszula , który zapewnia jawną swobodną rozdzielczość pola reszt k lokalnego pierścienia R w kategoriach ciągu regularnego.

Płaskość

Produkt napinacz jest inny niż dokładne funktor istotne w kontekście pierścień przemienny: o ogólnym R -module M , funktor

M ⊗ _R -

jest tylko prawidłowa dokładna. Jeśli jest dokładny, M nazywa się płaskim . Jeśli R jest lokalny, każdy skończony płaski moduł nie ma skończonej rangi, a więc jest rzutowy. Pomimo zdefiniowania w kategoriach algebry homologicznej, płaskość ma głębokie implikacje geometryczne. Na przykład, jeśli R- algebra S jest płaska, wymiary włókien

S / pS = S ⊗ _R R / p

(dla ideałów pierwszych p w R ) mają wymiar „oczekiwany”, czyli wym S - dim R + dim ( R / p ).

Nieruchomości

Zgodnie z twierdzeniem Wedderburna każdy skończony pierścień podziału jest przemienny, a zatem jest ciałem skończonym . Kolejny warunek zapewniający przemienność pierścienia ze względu na Jacobsona jest następujący: dla każdego elementu r z R istnieje liczba całkowita n > 1 taka, że r ⁿ = r . Jeśli r ² = r dla każdego r , pierścień nazywany jest pierścieniem boolowskim . Znane są również bardziej ogólne warunki gwarantujące przemienność pierścienia.

Uogólnienia

Pierścienie stopniowane przemienne

Spodnie to bordyzm między koła i dwóch rozłącznych okręgów. Klasy kobordyzmu, z iloczynem kartezjańskim jako mnożeniem i rozłącznym związkiem jako sumą, tworzą pierścień kobordyzmu .

Stopniowane pierścień R = ⨁ _{i ε Z} R _i jest nazywana stopniem-przemienne czy

ab = (−1) ^{deg a ⋅ deg b .}

Jeśli R _i są połączone różniczkami ∂ tak, że zachodzi abstrakcyjna postać reguły iloczynu , tj.

∂ ( ab ) = ∂ ( a ) b + (−1) ^{deg a} ∂ ( b ),

R nazywa się przemienną algebrą różniczkową (cdga). Przykładem jest zespół form różniczkowych na rozmaitości , z mnożeniem podanym przez produkt zewnętrzny , to cdga. Kohomologia cdga to stopniowany pierścień przemienny, czasami nazywany pierścieniem kohomologii . W ten sposób powstaje szeroka gama przykładów pierścieni klasyfikowanych. Na przykład, pierścień Lazard jest pierścień klas bordyzm złożonych rozdzielaczy.

Stopniowo-przemienny pierścień w odniesieniu do stopniowania przez Z / 2 (w przeciwieństwie do Z ) nazywany jest superalgebrą .

Podobnym pojęciem jest prawie przemienny pierścień , co oznacza, że R jest filtrowany w taki sposób, że powiązany pierścień stopniowany

gr R : = ⨁ F _i R / ⨁ F _{i −1} R

jest przemienna. Przykładem jest algebra Weyla i bardziej ogólne pierścienie operatorów różniczkowych .

Proste pierścienie przemienne

Symplicjalnego przemienne pierścień jest symplicjalnego obiekt w kategorii pierścień przemienny. Są cegiełkami do (łącznej) wyprowadzonej geometrii algebraicznej . Blisko spokrewnione, ale bardziej ogólne pojęcie to E _∞ -ring .

Zobacz też

Prawie pierścień , pewne uogólnienie pierścienia przemiennego.
Podzielność (teoria pierścieni) : pierwiastek zerowy , przykład: liczby podwójne
Ideały i moduły: Radykał ideału , równoważność Mority
Homomorfizmy pierścieniowe: integralnym elementem : Cayley Hamiltona twierdzenie , domeny integralnie zamknięty , Krull pierścieniowe , Krull-Akizuki twierdzenie
Liczbami pierwszymi: Prime unikanie lematu , Jacobson rodnik , nilradykał Spectrum: zwarta , Połączony pierścienia , kamienia różnicowe algebrą , Banacha-kamienia twierdzenie
Pierścienie lokalne: pierścień Gorensteina : Duality (matematyka) , Eben Matlis ; Dualizing moduł , twierdzenie Popescu jest , Artin przybliżenie twierdzenie .
„Applications” (pierścień przemienny powstające w matematyce) funkcje holomorficzne , algebraiczna K teorią , topologiczne K teorii , Podzielone struktury mocy , wektory Witt , Hecke Algebra , okres pierścienie Fontaine , Klaster Algebra , Splot Algebra (przemiennej grupie), patrz także algebra Frécheta

Uwagi

^ To pojęcie można powiązać z widmem operatora liniowego, patrz Spektrum C * -algebry i reprezentacji Gelfanda .

Cytaty

^ Matsumura (1989 , s. 143, § 7, uwagi)
^ Matsumura (1989 , § 19, Twierdzenie 48)
^ Lyubeznik (1989)
^ Eisenbud (1995 , wniosek 18.10, propozycja 18.13)
^ Zobacz także twierdzenie Serre-Swana .
^ Christensen, Striuli i Veliche (2010)
^ Jacobson 1945
^ Pinter-Lucke 2007

Bibliografia

Christensen, Lars Winther; Striuli, Janet; Veliche, Oana (2010), „Growth in the minimal injective resolution of a local ring”, Journal of the London Mathematical Society , Second Series, 81 (1): 24–44, arXiv : 0812.4672 , doi : 10.1112 / jlms / jdp058
Eisenbud, David (1995), Algebra przemienna. Z myślą o geometrii algebraicznej. , Graduate Texts in Mathematics , 150 , Berlin, New York: Springer-Verlag , ISBN 978-0-387-94268-1 , MR 1322960
Hochster, Melvin (2007), „Homological conjectures, old and new” (PDF) , Illinois J. Math. , 51 (1): 151–169, doi : 10.1215 / ijm / 1258735330 , zarchiwizowane z oryginału (PDF) 29.10.2019 , pobrane 01.08.2017
Jacobson, Nathan (1945), „Structure teoria algebraic algebras of bounded degree”, Annals of Mathematics , 46 (4): 695–707, doi : 10.2307 / 1969205 , ISSN 0003-486X , JSTOR 1969205
Lyubeznik, Gennady (1989), „A Overview of problems and results on the number of defining equations”, Representations, resolution and intertwining numbers , s. 375–390 , Zbl 0753.14001
Matsumura, Hideyuki (1989), Commutative Ring Theory , Cambridge Studies in Advanced Mathematics (2nd ed.), Cambridge University Press , ISBN 978-0-521-36764-6
Pinter-Lucke, James (2007), „Warunki przemienności pierścieni: 1950–2005”, Expositiones Mathematicae , 25 (2): 165–174, doi : 10.1016 / j.exmath.2006.07.001 , ISSN 0723-0869

Dalsza lektura

Atiyah, Michael ; Macdonald, IG (1969), Wprowadzenie do algebry przemiennej , Addison-Wesley Publishing Co.
Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Commutative Noetherian and Krull rings , Ellis Horwood Series: Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimension, multiplicity and homological methods , Ellis Horwood Series: Mathematics and its Applications., Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
Kaplansky, Irving (1974), Commutative rings (red. Poprawione), University of Chicago Press , MR 0345945
Nagata, Masayoshi (1975) [1962], Local rings , Interscience Tracts in Pure and Applied Mathematics, 13 , Interscience Publishers, pp. Xiii + 234, ISBN 978-0-88275-228-0 , MR 0155856
Zariski, Oscar ; Samuel, Pierre (1958–60), Commutative Algebra I, II , University series in Higher Mathematics, Princeton, NJ: D. van Nostrand, Inc. (Przedruk 1975-76 przez Springer jako tomy 28-29 Graduate Texts in Mathematics.)

[1] To pojęcie można powiązać z widmem operatora liniowego, patrz Spektrum C * -algebry i reprezentacji Gelfanda .

[2] Matsumura (1989 , s. 143, § 7, uwagi)

[3] Matsumura (1989 , § 19, Twierdzenie 48)

[4] Lyubeznik (1989)

[5] Eisenbud (1995 , wniosek 18.10, propozycja 18.13)

[6] Zobacz także twierdzenie Serre-Swana .

[7] Christensen, Striuli i Veliche (2010)

[8] Jacobson 1945

[9] Pinter-Lucke 2007

Languages

In other projects

Pierścień przemienny - Commutative ring

Definicja i pierwsze przykłady

Definicja

Pierwsze przykłady

Podzielność

Lokalizacje

Ideały i moduły

Moduły i ideały

Ideały

Główne domeny idealne

Pierścień czynnikowy

Pierścienie Noetherian

Pierścienie artyńskie

Widmo pierścienia przemiennego

Pierwotne ideały

Widmo

Schematy afiniczne

Wymiar

Homomorfizmy pierścieniowe

Skończone pokolenie

Lokalne pierścienie

Regularne pierścienie lokalne

Pełne skrzyżowania

Pierścienie Cohena-Macaulaya

Konstruowanie pierścieni przemiennych

Ukończenia

Pojęcia homologiczne

Moduły rzutowe i funktory Ext

Płaskość

Nieruchomości

Uogólnienia

Pierścienie stopniowane przemienne

Proste pierścienie przemienne

Zobacz też

Uwagi

Cytaty

Bibliografia

Dalsza lektura