Digon - Digon
| Zwykły digon | |
|---|---|
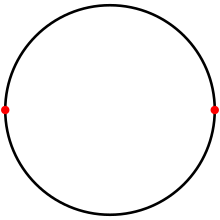 Na okręgu digon to teselacja z dwoma punktami antypodalnymi i dwoma krawędziami łuku 180 °.
| |
| Rodzaj | Regularny wielokąt |
| Krawędzie i wierzchołki | 2 |
| Symbol Schläfli | {2} |
| Diagram Coxetera | |
| Grupa symetrii | D 2 , [2], (* 2 •) |
| Podwójny wielokąt | Self-dual |
W geometrii , A Digon jest wielokąt z dwóch stron ( krawędzi ) i dwa wierzchołki . Jego konstrukcja jest zdegenerowana na płaszczyźnie euklidesowej, ponieważ obie strony byłyby zbieżne lub jedna lub obie musiałyby być zakrzywione; jednakże można to łatwo zwizualizować w przestrzeni eliptycznej.
Regularny digon ma oba kąty równe i oba boki równe i jest reprezentowany przez symbol Schläfli {2}. Może być zbudowany na kuli jako para łuków 180 stopni łączących punkty antypodalne , kiedy tworzy lune .
Digon jest najprostszym abstrakcyjnym polytopem o randze 2.
Ściętego Digon t {2} jest kwadratowy {4}. Naprzemienny Digon h {2} jest monogon {1}.
W geometrii euklidesowej
Digon może mieć jedną z dwóch reprezentacji wizualnych, jeśli zostanie umieszczony w przestrzeni euklidesowej.
Jedna reprezentacja jest zdegenerowana i wizualnie pojawia się jako podwójne pokrycie odcinka linii . Pojawiający się, gdy minimalna odległość między dwiema krawędziami wynosi 0, forma ta pojawia się w kilku sytuacjach. Ta forma podwójnego pokrycia jest czasami używana do definiowania zdegenerowanych przypadków niektórych innych polytopów; na przykład regularny czworościan można postrzegać jako antypryzmat utworzony z takiego digonu. Można go wyprowadzić z naprzemienności kwadratu (h {4}), ponieważ wymaga połączenia dwóch przeciwległych wierzchołków wspomnianego kwadratu. Kiedy wielowymiarowe polytopy zawierające kwadraty lub inne czworokątne figury są naprzemiennie, te digony są zwykle odrzucane i uważane za pojedyncze krawędzie.
Druga reprezentacja wizualna, o nieskończonej wielkości, to dwie równoległe linie rozciągające się do nieskończoności (i spotykające się projekcyjnie, tj. Mające wierzchołki w) nieskończoność, powstające, gdy najmniejsza odległość między dwiema krawędziami jest większa niż zero. Ta forma pojawia się w reprezentacji niektórych zdegenerowanych polytopów , czego godnym uwagi przykładem jest apeirogonalny hoszoedr , granica ogólnego hosoedru sferycznego w nieskończoności, złożonego z nieskończonej liczby digonów spotykających się w dwóch antypodalnych punktach w nieskończoności. Jednakże, ponieważ wierzchołki tych digonów znajdują się w nieskończoności, a zatem nie są ograniczone zamkniętymi segmentami linii, ta teselacja zwykle nie jest uważana za dodatkową regularną teselację płaszczyzny euklidesowej, nawet gdy jej podwójny rząd-2 apeirogonalny kafelek (nieskończony dwuścian ) jest.
Złożenie dwóch digonów "odcinków linii", jako dwóch możliwych wariantów kwadratu (zwróć uwagę na układ wierzchołków ).
Apeirogonal hosohedron , zawierający nieskończenie wielkości digony.
Każdy digon o prostych bokach jest regularny, mimo że jest zdegenerowany, ponieważ jego dwie krawędzie mają tę samą długość, a dwa kąty są równe (oba mają zero stopni). Jako taki, regularny digon jest konstruowalnym wielokątem .
Niektóre definicje wielokąta nie uznają digonu za właściwy wielokąt ze względu na jego degenerację w przypadku euklidesa.
W elementarnych wielościanach

Digon jako twarzy z wielościan jest zdegenerowany , ponieważ jest to zdegenerowany wielokąt. Ale czasami może mieć użyteczną topologiczną egzystencję w przekształcaniu wielościanów.
Jako sferyczna luna
Kulisty lune jest Digon którego dwa wierzchołki są antypodyczne punkty na kuli.
Kulisty wielościan wykonana z takich digons nazywa się hosohedron .
Sześć ścianek digonów na regularnym sześciokątnym hosoedrze .
Znaczenie teoretyczne
Digon jest ważnym konstruktem w topologicznej teorii sieci, takich jak grafy i powierzchnie wielościenne. Równoważności topologiczne można ustalić za pomocą procesu redukcji do minimalnego zestawu wielokątów, bez wpływu na globalne cechy topologiczne, takie jak wartość Eulera. Digon reprezentuje etap uproszczenia, w którym można go po prostu usunąć i zastąpić odcinkiem linii, bez wpływu na ogólną charakterystykę.
Te grupy cykliczne mogą być uzyskane w symetrii obrotowej wielokątów: symetrie obrotowej Digon utworzeniem grupy C 2 .
Zobacz też
Bibliografia
Cytaty
Bibliografia
- Herbert Busemann , Geometria geodezji. Nowy Jork, Academic Press, 1955
- Coxeter , Regular Polytopes (wydanie trzecie), Dover Publications Inc, 1973 ISBN 0-486-61480-8
- Weisstein, Eric W. „Digon” . MathWorld .
- AB Iwanow (2001) [1994], „Digon” , Encyklopedia Matematyki , EMS Press
Zewnętrzne linki
-
 Media związane z Digons w Wikimedia Commons
Media związane z Digons w Wikimedia Commons