Abstrakcyjny polytop - Abstract polytope

W matematyce An streszczenie Polytope jest algebraiczna częściowo uporządkowanym lub poset który rejestruje kombinatorycznych właściwości tradycyjnego Polytope bez określania właściwości czysto geometrycznych, takich jak kątów lub długości krawędzi. Polytope uogólnieniem wielokątów i wielościanów na dowolną liczbę wymiarów.

Mówi się, że zwykły geometryczny polytope jest realizacją w jakiejś rzeczywistej N-wymiarowej przestrzeni , zwykle euklidesowej , odpowiadającego mu abstrakcyjnego polytopu. Abstrakcyjna definicja dopuszcza pewne bardziej ogólne struktury kombinatoryczne niż tradycyjne definicje wielościanu, umożliwiając w ten sposób wiele nowych obiektów, które nie mają odpowiednika w tradycyjnej teorii.

Koncepcje wstępne

Politopy tradycyjne kontra abstrakcyjne

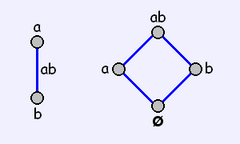
W geometrii euklidesowej wszystkie z sześciu przedstawionych czworokątów są różne. Jednak mają wspólną strukturę w naprzemiennym łańcuchu czterech wierzchołków i czterech boków, co daje im ich nazwę. Mówi się, że są izomorficzne lub „zachowujące strukturę”.

Ta wspólna struktura może być reprezentowana w leżącym pod spodem abstrakcyjnym polytope, czysto algebraicznym, częściowo uporządkowanym zbiorze, który wychwytuje wzór połączeń lub przypadków pomiędzy różnymi elementami strukturalnymi. Mierzalne właściwości tradycyjnych polytopów, takie jak kąty, długości krawędzi, skośność, prostoliniowość i wypukłość nie mają znaczenia dla abstrakcyjnego polytope.

To, co jest prawdą w przypadku politopów tradycyjnych (zwanych również politopami klasycznymi lub geometrycznymi), może nie być takie w przypadku abstrakcyjnych i na odwrót. Na przykład tradycyjny polytope jest regularny, jeśli wszystkie jego fasety i figury wierzchołków są regularne, ale niekoniecznie tak jest w przypadku abstrakcyjnego polytope.

Realizacje

Mówi się, że tradycyjny politop geometryczny jest realizacją związanego z nim abstrakcyjnego politopu. Realizacja to odwzorowanie lub wstrzyknięcie abstrakcyjnego obiektu w rzeczywistą przestrzeń, typowo euklidesową , w celu skonstruowania tradycyjnego polytopu jako rzeczywistej figury geometrycznej.

Sześć pokazanych czworokątów to odrębne realizacje abstrakcyjnego czworoboku, z których każdy ma inne właściwości geometryczne. Niektóre z nich nie mieszczą się w tradycyjnych definicjach czworoboku i podobno są realizacjami niewiernymi . Konwencjonalny polytope to wierna realizacja.

Twarze, stopnie i porządek

W abstrakcyjnym wielotopie każdy element strukturalny - wierzchołek, krawędź, komórka itp. jest powiązany z odpowiednim członkiem lub elementem zbioru. Termin ściana często odnosi się do dowolnego takiego elementu, np. wierzchołka (0-ściana), krawędzi (1-ściana) lub ogólnej k- ściany, a nie tylko wielokąta 2-ściana.

Ściany są uszeregowane zgodnie z ich rzeczywistym wymiarem: wierzchołki mają rangę = 0, krawędzie = 1 i tak dalej.

Ściany opadające o różnej randze, na przykład wierzchołek F krawędzi G, są uporządkowane według relacji F < G. Mówi się, że F jest podpowierzchnią G lub G ma podpowierzchnię F.

Mówi się, że F, G są incydentalne, jeśli F = G lub F < G lub G < F. To użycie „przypadku” występuje również w geometrii skończonej , chociaż różni się od tradycyjnej geometrii i niektórych innych dziedzin matematyki. Na przykład w kwadracie abcd krawędzie ab i bc nie są abstrakcyjnie incydentalne (chociaż oba są incydentalne z wierzchołkiem b ).

Wielotop jest wtedy definiowany jako zbiór ścian P o relacji porządku <, który spełnia pewne dodatkowe aksjomaty. Formalnie P (z < ) będzie (ścisły) częściowo uporządkowanym zbiorem lub poset .

Najmniejsze i największe twarze

Tak jak liczba zero jest konieczna w matematyce, tak też każdy zbiór ma zbiór pusty ∅ jako podzbiór. W abstrakcyjnym politopie ∅ jest umownie identyfikowany jako najmniejsza lub zerowa ściana i jest podpowierzchnią wszystkich pozostałych. Ponieważ najmniejsza ściana jest o jeden poziom poniżej wierzchołków lub 0 ścian, jej ranga wynosi -1 i może być oznaczona jako F _-1 . Zatem F _-1 ≡ ∅ i abstrakcyjny polytope również zawierają pusty zbiór jako element. Zwykle nie jest realizowany.

Jest też jedna ściana, której wszystkie pozostałe są podpowierzchniami. Nazywa się to największą twarzą. W n- wymiarowym wielotopie największa ściana ma rangę = n i może być oznaczona jako F _n . Bywa realizowany jako wnętrze figury geometrycznej.

Te najmniejsze i największe twarze są czasami nazywane twarzami niewłaściwymi , a wszystkie inne są twarzami właściwymi .

Prosty przykład

Ściany abstrakcyjnego czworoboku lub kwadratu pokazano w poniższej tabeli:

Typ twarzy	Ranga ( k )	Liczyć	k - twarze
Najmniej	-1	1	F- 1
Wierzchołek	0	4	a , b , c , d
Krawędź	1	4	W, X, Y, Z
Największy	2	1	g

Relacja < składa się ze zbioru par, które tutaj obejmują

F _-1 < a , ... , F _-1 <X, ... , F _-1 <G, ... , b <Y, ... , c <G, ... , Z<G.

Stosunki rzędu są przechodnie , czyli F <G i G <H implikuje, że F <H. Dlatego, aby określić hierarchię twarze, nie jest konieczne, aby dać każdy przypadek F <H, tylko parami, gdzie jeden jest następcą od drugi, tj. gdzie F < H i brak G spełnia F < G < H.

Krawędzie W, X, Y i Z są czasami zapisywane odpowiednio jako ab , ad , bc i cd , ale taka notacja nie zawsze jest odpowiednia.

Wszystkie cztery krawędzie są strukturalnie podobne i to samo dotyczy wierzchołków. Figura ma więc symetrie kwadratu i jest zwykle nazywana kwadratem.

Diagram Hassego

Mniejsze posety, a w szczególności wielokąty, są często najlepiej wizualizowane na diagramie Hassego , jak pokazano. Zgodnie z konwencją, ściany o równej randze są umieszczane na tym samym poziomie w pionie. Każda „linia” między ścianami, powiedzmy F, G, wskazuje na relację uporządkowania < taką, że F < G gdzie F jest poniżej G na diagramie.

Diagram Hassego definiuje unikalny poset, a zatem w pełni oddaje strukturę politopu. Politopy izomorficzne dają początek izomorficznym diagramom Hassego i na odwrót. To samo nie jest generalnie prawdziwe w przypadku graficznej reprezentacji politopów.

Ranga

Stopień lica K jest zdefiniowana jako ( m  - 2), w którym m oznacza liczbę maksymalnie powierzchni w każdym łańcuchu (F”, F”, ..., K) spełniającego F”<K” <... < F. F' jest zawsze najmniejszą ścianką, F- ₁ .

Stopień abstrakcyjnego Polytope P jest maksymalny stopień n każdej powierzchni. Jest to zawsze ranga największej twarzy F _n .

Ranga twarzy lub polytope zwykle odpowiada wymiarowi jej odpowiednika w tradycyjnej teorii.

W przypadku niektórych rang ich typy twarzy wymieniono w poniższej tabeli.

Ranga	-1	0	1	2	3	...	n - 2	n - 1	n
Typ twarzy	Najmniej	Wierzchołek	Krawędź	?	Komórka		Podfasada lub grzbiet	Aspekt	Największy

† Tradycyjnie „twarz” oznacza twarz 2 lub 2 rangi. W teorii abstrakcyjnej termin „twarz” oznacza twarz dowolnej rangi.

Flagi

Flaga jest maksymalny łańcuch twarze, czyli (całkowicie) uporządkowanym zbiorem * F twarze, każdy z subface następnego (jeśli w ogóle), a takie, że Ψ nie jest podzbiorem każdej większej sieci. Biorąc pod uwagę dowolne dwie różne twarze F, G we fladze, albo F < G lub F > G.

Na przykład { ø , a , ab , abc } to flaga w trójkącie abc .

Dla danego politopu wszystkie flagi zawierają taką samą liczbę ścian. Inne pozy na ogół nie spełniają tego wymogu.

Sekcje

Dowolny podzbiór P' posetu P jest posetem (o tej samej relacji <, ograniczonej do P').

W abstrakcyjnym wielotopie, przy danych dowolnych dwóch ścianach F , H z P o F ≤ H , zbiór { G | F ≤ G ≤ H } nazywany jest sekcja z P i oznaczone H / F . (W teorii porządkowej odcinek nazywa się przedziałem domkniętym posetu i oznacza [ F , H ].

Na przykład w pryzmacie abcxyz (patrz schemat) przekrój xyz / ø (podświetlony na zielono) to trójkąt

{ ø , x , y , z , xy , xz , yz , xyz }.

K -section to odcinek rankingu k .

P jest więc częścią samego siebie.

Ta koncepcja przekroju nie ma takiego samego znaczenia jak w tradycyjnej geometrii.

Fasety

Aspekt dla danego j -Face F jest ( j - 1 ) -section F / ∅, gdzie F _j jest największa twarz.

Na przykład w trójkącie abc aspektem w ab jest ab / b = { ∅, a, b, ab }, który jest segmentem linii.

Rozróżnienie między F i F /∅ zwykle nie jest znaczące i często traktuje się je jako identyczne.

Liczby wierzchołków

Postać wierzchołka w danym wierzchołek V jest ( n -1) -section F _n / V , gdzie M _n jest największa powierzchnia.

Na przykład w trójkącie abc figura wierzchołka w punkcie b to abc / b = { b, ab, bc, abc }, co jest odcinkiem linii. Figury wierzchołkowe sześcianu są trójkątami.

Powiązanie

Poset P jest połączony, jeśli P ma rangę ≤ 1 lub, przy danych dwóch ścianach właściwych F i G, istnieje sekwencja ścian właściwych

H ₁ , H ₂ , ... ,H _k

takie, że K = H ₁ G = H, _K , a każdy z H _i , i <k, padającego z następcy.

Powyższe warunek, zapewnia, że para rozłącznych trójkąty abc i XYZ iS nie jest (pojedynczy) Polytope.

Poset P jest silnie połączony, jeśli każda sekcja P (w tym samo P) jest połączona.

Z tym dodatkowym wymogiem wykluczone są również dwie piramidy, które mają tylko jeden wierzchołek. Jednak, na przykład, dwie kwadratowe piramidy mogą być "przyklejone" do ich kwadratowych ścian - dając ośmiościan. „Wspólna twarz” nie jest więc twarzą ośmiościanu.

Formalna definicja

Streszczenie Polytope jest częściowy porządek , którego elementy nazywamy twarze , spełniającą 4 aksjomaty:

1. Ma najmniejszą twarz i największą twarz .
2. Wszystkie flagi zawierają taką samą liczbę twarzy.
3. Jest silnie powiązany .
4. Jeśli szeregi dwóch ścian a > b różnią się o 2, to dokładnie 2 ściany leżą dokładnie pomiędzy a i b .

N -polytope jest Polytope od rangi n .

Uwagi

W przypadku politopu zerowego najmniejsza i największa ściana to ten sam pojedynczy element .

Aksjomat 2 jest równoważny stwierdzeniu, że poset jest posetem stopniowanym .

Biorąc pod uwagę inne aksjomaty, Aksjomat 3 jest równoważny silnemu połączeniu flagi , co nieformalnie oznacza:

Dla dowolnej sekcji polytope (w tym samego polytope) dowolną flagę można zmienić na dowolną inną, zmieniając tylko jedną twarz na raz.

Aksjomat 4 jest znany jako „właściwość diamentu”, ponieważ Diagram Hassego a , b i ścianki pomiędzy nim mają kształt rombu.

Z aksjomatów można wykazać, że każda sekcja jest wielotopem i że Rank( G / F ) = Rank( G ) − Rank( F ) − 1.

Abstrakcyjny polytop skojarzony z prawdziwym polytopem wypukłym jest również nazywany jego siatką czołową .

Najprostsze politopy

Pozycja < 1

Jest tylko jeden poset dla każdej rangi -1 i 0. Są to odpowiednio pusta ściana i punkt. Nie zawsze są one uważane za ważne abstrakcyjne politopy.

Pozycja 1: segment linii

Istnieje tylko jeden wielotop o randze 1, który jest segmentem liniowym. Ma najmniejszą ścianę, tylko dwie zerowe ściany i największą ścianę, na przykład {ø, a, b, ab }. Wynika z tego, że wierzchołki a i b mają rangę 0, a największa ściana ab , a więc i poset, mają rangę 1.

Poziom 2: wielokąty

Dla każdego p , 3 ≤ p < , mamy (abstrakcyjny odpowiednik) tradycyjny wielokąt z p wierzchołków i p krawędzi lub p -kąt. Dla p = 3, 4, 5, ... mamy trójkąt, kwadrat, pięciokąt, .... ${\displaystyle \infty}$

Dla p = 2 mamy digon , a p = otrzymujemy apeirogon . ${\displaystyle \infty}$

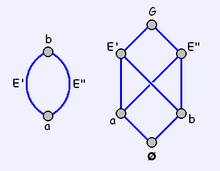
Digon

Digon jest wielokąt z zaledwie 2 krawędziami. W przeciwieństwie do innych wielokątów obie krawędzie mają te same dwa wierzchołki. Z tego powodu jest zdegenerowany w płaszczyźnie euklidesowej .

Ściany są czasami opisywane za pomocą "notacji wierzchołkowej" - np. { ø , a , b , c , ab , ac , bc , abc } dla trójkąta abc . Metoda ta ma tę zaletę, sugerując się < relację.

Z cyfrą ta notacja wierzchołkowa nie może być używana . Należy nadać ścianom indywidualne symbole oraz określić pary podpowierzchni F < G.

Zatem digon jest zdefiniowany jako zbiór { ø , a , b , E', E”, G} o relacji < danej przez

{ ø < a , ø < b , a <E', a <E", b <E', b <E", E'<G, E"<G}

gdzie E' i E" są dwiema krawędziami, a G największą ścianą.

Ta potrzeba identyfikowania każdego elementu politopu za pomocą unikalnego symbolu dotyczy wielu innych abstrakcyjnych politopów i dlatego jest powszechną praktyką.

Polytope można w pełni opisać za pomocą notacji wierzchołków tylko wtedy, gdy każda ściana pada na unikalny zestaw wierzchołków . Mówi się, że politop posiadający tę właściwość jest atomistyczny .

Przykłady wyższej rangi

Zbiór j- ścian (-1 ≤ j ≤ n ) tradycyjnego n- politopu tworzy abstrakcyjny n- politop.

Pojęcie abstrakcyjnego politopu jest bardziej ogólne i obejmuje również:

• Apeirotopes lub nieskończone polytopes , które obejmują teselacje (kafelki)
• Właściwe rozkłady nieograniczonych rozmaitości, takich jak torus lub rzeczywista płaszczyzna rzutowa .
• Wiele innych obiektów, takich jak 11-ogniwowa i 57-ogniwowa , których nie można wiernie zrealizować w przestrzeniach euklidesowych.

Hosoedry i hozotopy

Digon jest uogólniony przez jednościan i hozotopy wyższych wymiarów, z których wszystkie mogą być zrealizowane jako wielościany sferyczne – teselują sferę.

Politopy projekcyjne

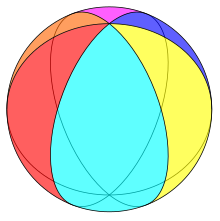
Cztery przykłady nietradycyjnych abstrakcyjnych wielościanów to Hemicube (pokazany), Hemi-octahedron , Hemi-dodecahedron i Hemi-icosahedron . Są to projekcyjne odpowiedniki brył platońskich , które mogą być realizowane jako (globalnie) rzutowe wielościany – teselują one rzeczywistą płaszczyznę rzutową .

Hemicube jest kolejnym przykładem, w którym notacja wierzchołków nie może być użyta do zdefiniowania wielościanu - wszystkie 2 ściany i 3 ściany mają ten sam zestaw wierzchołków.

Dwoistość

Każdy geometryczny polytope ma podwójnego bliźniaka. Abstrakcyjnie, dual to ten sam polytope, ale z rankingiem odwróconym w kolejności: diagram Hassego różni się tylko adnotacjami. W n -politopie, każda z oryginalnych k -ścian mapuje się na ( n  −  k  − 1)-ścian w układzie dualnym. Tak więc, na przykład, n- twarz odwzorowuje się na (-1)-twarz. Podwójna podwójna jest ( izomorficzna z) oryginałem.

Wielotop jest samodualistyczny, jeśli jest taki sam, tj. izomorficzny z jego dualem. Stąd diagram Hassego samodwójnego polytopu musi być symetryczny wokół osi poziomej w połowie drogi między górą a dołem. Kwadratowa piramida w powyższym przykładzie jest samopodwójna.

Figura wierzchołkowa w wierzchołku V jest podwójną fasetką, do której V mapuje w podwójnym polytope.

Streszczenie regularne polytopes

Formalnie abstrakcyjny politop jest zdefiniowany jako „regularny”, jeśli jego grupa automorfizmu działa przechodnie na zbiorze jego flag. W szczególności, każde dwa k -faces F , G danego n -polytope są „takie same”, to znaczy, że nie ma automorfizmem który odwzorowuje F do G . Kiedy abstrakcyjny politop jest regularny, jego grupa automorfizmu jest izomorficzna z ilorazem grupy Coxetera .

Wszystkie politopy rzędu ≤ 2 są regularne. Najbardziej znane wielościany regularne to pięć brył platońskich. Hemisześcian (pokazany) jest również regularny.

Nieformalnie, dla każdej rangi k oznacza to, że nie ma sposobu na odróżnienie żadnej ściany k od innych - ściany muszą być identyczne, muszą mieć identycznych sąsiadów i tak dalej. Na przykład sześcian jest regularny, ponieważ wszystkie ściany są kwadratami, wierzchołki każdego kwadratu są dołączone do trzech kwadratów, a każdy z tych kwadratów jest dołączony do identycznego układu innych ścian, krawędzi i wierzchołków i tak dalej.

Sam ten warunek jest wystarczający, aby zapewnić, że każdy regularny abstrakcyjny polytope ma izomorficzne regularne ( n- 1) ściany i izomorficzne regularne figury wierzchołków.

Jest to warunek słabszy niż prawidłowość dla tradycyjnych politopów, ponieważ odnosi się do grupy (kombinatorycznej) automorfizmu, a nie do (geometrycznej) grupy symetrii. Na przykład, każdy abstrakcyjny wielokąt jest regularny, ponieważ kąty, długości krawędzi, krzywizna krawędzi, skośność itp. nie istnieją dla abstrakcyjnych wielokątów.

Istnieje kilka innych słabszych pojęć, z których niektóre nie są jeszcze w pełni ustandaryzowane, takie jak półregularny , quasi-regularny , jednolity , chiralny i archimedesowy, które mają zastosowanie do politopów, które mają równoważne niektóre, ale nie wszystkie ich twarze w każdej randze.

Nieregularny przykład

Biorąc pod uwagę ilość uwagi, jaką poświęca się regularnym polytopes, można by prawie pomyśleć, że wszystkie polytopes są regularne. W rzeczywistości zwykłe politopy to tylko bardzo szczególne przypadki.

Najprostszym nieregularnym polytopem jest kwadratowa piramida , chociaż nadal ma wiele symetrii.

Pokazano przykład wielościanu bez nietrywialnych symetrii — żadna para wierzchołków, krawędzi lub 2 ścian nie jest „taka sama”, jak zdefiniowano powyżej. To chyba najprostszy taki politop.

Realizacja

Zbiór punktów V w przestrzeni euklidesowej wyposażony w odjętą od zbioru wierzchołków abstrakcyjnego politopu P taki, że automorfizmy P indukują permutacje izometryczne V, nazywamy realizacją abstrakcyjnego wielotopu. Dwie realizacje nazywane są kongruentnymi, jeśli naturalna bijektacja między ich zestawami wierzchołków jest indukowana przez izometrię ich otoczenia przestrzeni euklidesowych.

Jeśli abstrakcyjny n- politop jest realizowany w przestrzeni n- wymiarowej, tak że układ geometryczny nie łamie żadnych zasad obowiązujących w tradycyjnych politopach (takich jak zakrzywione ściany lub grzbiety o zerowym rozmiarze), to mówi się, że realizacja jest wierna . Ogólnie rzecz biorąc, tylko ograniczony zbiór abstrakcyjnych politopów rzędu n może być wiernie zrealizowany w dowolnej danej n -przestrzeni. Nierozstrzygniętym problemem jest scharakteryzowanie tego efektu.

W przypadku regularnego abstrakcyjnego wielotopu, jeśli kombinatoryczne automorfizmy abstrakcyjnego wielotopu są realizowane przez geometryczne symetrie, wówczas figura geometryczna będzie regularnym wielokątem.

Przestrzeń modułowa

Grupa symetrii G realizacji V abstrakcyjnego politopu P jest generowana przez dwa odbicia, których iloczyn przekłada każdy wierzchołek P na następny. Iloczyn dwóch odbić można rozłożyć jako iloczyn niezerowej translacji, skończenie wielu obrotów i ewentualnie trywialnego odbicia.

Generalnie przestrzeń moduli realizacji abstrakcyjnego wielotopu jest wypukłym stożkiem o nieskończonym wymiarze. Stożek realizacji abstrakcyjnego politopu ma nieskończony wymiar algebraiczny i nie może być zamknięty w topologii euklidesowej .

Problem amalgamacji i uniwersalne politopy

Ważnym pytaniem w teorii abstrakcyjnych polytopes jest problem amalgamacji . To seria pytań, takich jak

Czy dla danych abstrakcyjnych politopów K i L istnieją jakieś politopy P, których fasetki to K i których figury wierzchołków to L  ?

Jeśli tak, to czy wszystkie są skończone?

Jakie są skończone?

Na przykład, jeśli K jest kwadratem, a L jest trójkątem, odpowiedzi na te pytania to

Tak, istnieją politopy P z kwadratowymi ścianami, połączone po trzy na wierzchołek (czyli są to politopy typu {4,3}).

Tak, wszystkie są skończone, w szczególności

Jest sześcian z sześcioma kwadratowymi ścianami, dwunastoma krawędziami i ośmioma wierzchołkami oraz półsześcian z trzema ścianami, sześcioma krawędziami i czterema wierzchołkami.

Wiadomo, że jeśli odpowiedź na pierwsze pytanie brzmi „Tak” dla niektórych regularnych K i L , to istnieje unikalny politop, którego fasetki to K i którego figury wierzchołkowe to L , zwany uniwersalnym polytope z tymi fasetami i figurami wierzchołków, który obejmuje wszystkie inne takie politopy. To znaczy, załóżmy, że P jest uniwersalnym polytope z fasetami K i figurami wierzchołków L . Następnie można zapisać dowolny inny politop Q z tymi ściankami i figurami wierzchołków Q = P / N , gdzie

• N jest podgrupą grupy automorfizmu P , a
• P / N to zbiór orbit elementów P pod działaniem N , z częściowym porządkiem indukowanym przez P .

P = P / N nazywa się iloraz z P i mówimy P obejmuje Q .

Biorąc pod uwagę ten fakt, poszukiwania politopów o określonych fasetach i figurach wierzchołkowych zwykle przebiegają następująco:

1. Spróbuj znaleźć odpowiedni uniwersalny polytope
2. Próba sklasyfikowania jego ilorazów.

Te dwa problemy są na ogół bardzo trudne.

Wracając do powyższego przykładu, jeśli K jest kwadratem, a L jest trójkątem, uniwersalny politop { K , L } to sześcian (zapisany również {4,3}). Hemisześcian to iloraz {4,3}/ N , gdzie N jest grupą symetrii (automorfizmów) sześcianu z tylko dwoma elementami - tożsamością i symetrią, która odwzorowuje każdy róg (lub krawędź lub ścianę) na jego przeciwieństwo .

Jeśli zamiast tego L jest również kwadratem, uniwersalny politop { K , L } (czyli {4,4}) jest teselacją płaszczyzny euklidesowej przez kwadraty. Teselacja ta ma nieskończenie wiele ilorazów z kwadratowymi ścianami, cztery na wierzchołek, niektóre regularne, inne nie. Z wyjątkiem samego uniwersalnego polytope, wszystkie odpowiadają różnym sposobom teselacji torusa lub nieskończenie długiego walca z kwadratami.

11-komorowy i 57-komorowy

11 komórki , niezależnie odkryta przez HSM Coxeter'a i Branko Grünbaum jest streszczenie 4-Polytope. Jego fasety to hemiicosahedry. Ponieważ jej fasety są topologicznie płaszczyznami rzutowymi zamiast sfer, komórka 11 nie jest teselacją żadnej rozmaitości w zwykłym sensie. Zamiast tego 11-komórka jest lokalnie projekcyjnym wielotopem. 11-komórka jest nie tylko piękna w sensie matematycznym, ale jest również historycznie ważna jako jeden z pierwszych odkrytych nietradycyjnych abstrakcyjnych politopów. Jest samodwoisty i uniwersalny: jest jedynym wielotopem z fasetami hemi-dodekaedrycznymi i figurami hemi-dodekaedrycznymi wierzchołkami.

57-komórka jest także własny podwójny, z Hemi-dodecahedral aspektach. Został odkryty przez HSM Coxeter wkrótce po odkryciu 11-komórki. Podobnie jak 11-komórka, jest również uniwersalna, będąc jedynym politopem z fasetami hemi-dodekaedrycznymi i figurami hemi-cosahedralnymi. Z drugiej strony istnieje wiele innych politopów z fasetami półdodekaedrycznymi i typem Schläfliego {5,3,5}. Uniwersalny wielotop z fasetami hemi-dodekaedrycznymi i figurami wierzchołkowymi icosahedral (nie hemi-cosahedral) jest skończony, ale bardzo duży, z fasetami 10006920 i o połowę mniejszą liczbą wierzchołków.

Lokalna topologia

Historycznie problem amalgamacji był realizowany zgodnie z lokalną topologią . Oznacza to, że zamiast ograniczać K i L do określonych politopów, mogą one być dowolnymi politopami o danej topologii , to znaczy dowolnym politopem teselującym daną rozmaitość . Jeśli K i L są sferyczne (czyli teselacje sfery topologicznej ), to P nazywamy lokalnie sferycznym i odpowiada teselacji jakiejś rozmaitości. Na przykład, jeśli K i L są kwadratami (a więc topologicznie są tożsame z okręgami), P będzie teselacją płaszczyzny, torusa lub butelki Kleina przez kwadraty. Teselacja n- wymiarowej rozmaitości jest w rzeczywistości  politopem rzędu n +1. Jest to zgodne z powszechną intuicją, że bryły platońskie są trójwymiarowe, chociaż można je traktować jako teselacje dwuwymiarowej powierzchni kuli.

Ogólnie rzecz biorąc, abstrakcyjny politop jest nazywany lokalnie X, jeśli jego fasetki i figury wierzchołków są topologicznie albo sferami, albo X , ale nie obiema sferami. 11 komórek i 57 komórek przykłady Pozycja 4 (to jest cztery wymiarowe) lokalnie rzutowe polytopes, jako ich aspekty i liczby wierzchołków są TESELACJE z rzeczywistych projekcyjnych płaszczyznach . W tej terminologii jest jednak słabość. Nie pozwala to w łatwy sposób opisać politopu, którego fasetami są tori, a figury wierzchołków są na przykład płaszczyznami rzutowymi. Jeszcze gorzej, jeśli różne aspekty mają różne topologie lub w ogóle nie mają dobrze zdefiniowanej topologii. Jednak poczyniono znaczne postępy w zakresie pełnej klasyfikacji lokalnie toroidalnych politopów regularnych

Wymień mapy

Niech Ψ będzie flagą abstrakcyjnego n -politopu i niech −1 <  i  <  n . Z definicji abstrakcyjnego wielotopu można wykazać, że istnieje unikatowa flaga różniąca się od Ψ elementem o randze i , a w przeciwnym razie taka sama. Jeśli nazwiemy tę flagę Ψ ^{( i )} , to definiuje to zbiór map na flagach polytopes, powiedzmy φ _i . Mapy te nazywane są mapami wymiany , ponieważ zamieniają się parami flag : ( Ψφ _i ) φ _i  =  Ψ zawsze. Kilka innych właściwości map giełdowych:

• φ _i ² to mapa tożsamości
• Φ _i generowania grupy . (Działanie tej grupy na flagach polytope jest przykładem tak zwanej akcji flagowej grupy na polytope)
• Jeżeli | ja  −  j | > 1, φ _i φ _j = φ _j φ _i
• Jeżeli α jest automorfizmem politopu , to αφ _i = φ _i α
• Jeśli politop jest regularny, grupa generowana przez φ _i jest izomorficzna z grupą automorfizmu, w przeciwnym razie jest ściśle większa.

Mapy wymiany, a w szczególności akcja flagi, mogą być użyte do udowodnienia, że dowolny abstrakcyjny polytope jest ilorazem jakiegoś regularnego polytope.

Macierze incydentów

Wielotop może być również reprezentowany przez zestawienie jego wystąpień .

Następująca macierz padania jest macierzą trójkąta:

	ø	a	b	C	ab	pne	może	ABC
ø	1	1	1	1	1	1	1	1
a	1	1	0	0	1	0	1	1
b	1	0	1	0	1	1	0	1
C	1	0	0	1	0	1	1	1
ab	1	1	1	0	1	0	0	1
pne	1	0	1	1	0	1	0	1
może	1	1	0	1	0	0	1	1
ABC	1	1	1	1	1	1	1	1

Tabela pokazuje 1 tam, gdzie jedna ściana jest podścianą innej lub odwrotnie (więc tabela jest symetryczna względem przekątnej) - tak naprawdę tabela zawiera nadmiarowe informacje ; wystarczyłoby pokazać tylko 1, gdy ściana wiersza ≤ ściana kolumny.

Ponieważ zarówno ciało, jak i pusty zbiór są sprzeczne ze wszystkimi innymi elementami, pierwszy wiersz i kolumna, a także ostatni wiersz i kolumna są trywialne i można je wygodnie pominąć.

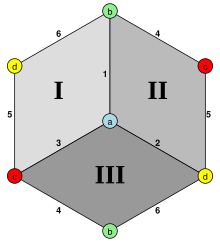
Kwadratowa Piramida

Dalsze informacje są uzyskiwane poprzez liczenie każdego zdarzenia. Ten numerative wykorzystanie Umożliwia on symetrii ugrupowania, jak w diagram hassego o kwadratowym piramidy : Jeżeli wierzchołki B, C, D i E są uważane symetrycznie równoważne w abstrakcyjnej Polytope, a krawędzie f, g, h, j będą grupowane razem, a także krawędzie k, l, m i n, I wreszcie trójkąty P , Q , R , i S . Zatem odpowiadająca macierz zapadalności tego abstrakcyjnego politopu może być pokazana jako:

	A	B,C,D,E	f,g,h,j	k,l,m,n	P , Q , R , S	T
A	1	*	4	0	4	0
B,C,D,E	*	4	1	2	2	1
f,g,h,j	1	1	4	*	2	0
k,l,m,n	0	2	*	4	1	1
P , Q , R , S	1	2	2	1	4	*
T	0	4	0	4	*	1

W tej reprezentacji macierzy skumulowanych przypadków wpisy diagonalne reprezentują całkowitą liczbę każdego typu elementu.

Elementy różnego typu o tej samej randze wyraźnie nigdy nie są przypadkowe, więc wartość zawsze będzie wynosić 0, jednak aby ułatwić rozróżnienie takich relacji, zamiast 0 używana jest gwiazdka (*).

Wpisy subdiagonalne w każdym rzędzie reprezentują zliczenia padania odpowiednich podelementów, podczas gdy wpisy superdiagonalne reprezentują liczbę odpowiednich elementów na wierzchołku, krawędzi lub jakiejkolwiek innej figurze.

Już ta prosta piramida kwadratowa pokazuje, że macierze zakumulowanej symetrii częstości nie są już symetryczne. Ale nadal istnieje prosta relacja między bytami (poza uogólnionymi wzorami Eulera na przekątną, odpowiednio elementy subdiagonalne każdego rzędu, odpowiednio elementy superdiagonalne każdego rzędu - przynajmniej wtedy, gdy nie ma dziur, gwiazd itp. brane pod uwagę), ponieważ dla każdej takiej macierzy zapadalności obowiązuje : ${\ Displaystyle I = (I_ {ij})}$

${\ Displaystyle I_ {ii} \ cdot I_ {ij} = ja_ {ji} \ cdot I_ {jj} \ \ (i <j).}$

Historia

W latach 60. Branko Grünbaum zaapelował do społeczności geometrycznej o rozważenie uogólnień koncepcji regularnych polytopes , które nazwał polystromata . Opracował teorię polistromaty, pokazując przykłady nowych obiektów, w tym 11-komórkę .

11-komórka jest self-Dual 4-Polytope którego aspekty nie są icosahedra , ale są „ hemi-icosahedra ” - to znaczy, że to jeden kształt dostaje jeśli weźmie się pod uwagę przeciwstawne twarze icosahedra być właściwie sama twarz ( Grünbauma, 1977). Kilka lat po odkryciu Grunbaum jest z 11 komórek , HSM Coxeter odkryto podobny Polytope, z 57-komórka (Coxeter 1982, 1984), a następnie niezależnie odkryte 11-komórka.

Kiedy podwaliny położyły wcześniejsze prace Branko Grünbauma , HSM Coxetera i Jacquesa Titsa, podstawowa teoria struktur kombinatorycznych, znanych obecnie jako abstrakcyjne wielotopy, została po raz pierwszy opisana przez Egona Schulte w jego rozprawie doktorskiej z 1980 roku. Zdefiniował w nim „zespoły o regularnym padaniu” i „politopy o regularnym padaniu”. Następnie on i Peter McMullen opracowali podstawy teorii w serii artykułów naukowych, które później zebrano w książkę. Od tego czasu wielu innych badaczy wniosło swój własny wkład, a pierwsi pionierzy (w tym Grünbaum) również zaakceptowali definicję Schulte jako „poprawną”.

Od tego czasu badania nad teorią abstrakcyjnych politopów skoncentrowały się głównie na politopach regularnych , czyli takich, których grupy automorfizmu działają przechodnie na zbiorze flag tego politopu.

Zobacz też

• Poseta Eulera
• Oceniony post
• Zwykły polytope

Uwagi

Bibliografia