Wielościan toroidalny - Toroidal polyhedron

Wielościenny torus może być skonstruowany tak, aby przybliżyć powierzchnię torusa, z sieci czworobocznych ścian, jak ten przykład 6x4.

W geometrii , A toroidalny wielościan jest A wielościan , który jest również toroidalny (a g -holed torusa ), posiadające topologiczne rodzajową 1 lub większą. Godne uwagi przykłady obejmują wielościany Császár i Szilassi .

Różnice w definicji

Wielościany toroidalne definiuje się jako zbiory wielokątów, które spotykają się na krawędziach i wierzchołkach, tworząc rozmaitość . Oznacza to, że każda krawędź powinna być dzielona przez dokładnie dwa wielokąty, a połączenie każdego wierzchołka powinno być pojedynczym cyklem, który zmienia się między krawędziami i wielokątami, które spotykają się w tym wierzchołku. W przypadku wielościanów toroidalnych ten kolektor jest powierzchnią orientowaną . Niektórzy autorzy ograniczają wyrażenie „toroidalny wielościany” oznacza dokładniej wielościany topologicznie równoważne (1) rodzaju torusa .

W tym obszarze istotne jest odróżnienie zatopionych wielościanów toroidalnych, których powierzchnie są płaskimi wielokątami w trójwymiarowej przestrzeni euklidesowej , które się nie przecinają, od abstrakcyjnych wielościanów , powierzchni topologicznych bez określonej realizacji geometrycznej. Pośrednie między tymi dwoma skrajnościami są wielościany utworzone przez wielokąty geometryczne lub wielokąty gwiaździste w przestrzeni euklidesowej, które mogą się przecinać.

We wszystkich tych przypadkach toroidalny charakter wielościanu można zweryfikować na podstawie jego orientacji i braku dodatniej charakterystyki Eulera . Charakterystyka Eulera uogólnia się do V − E + F = 2 − 2 N , gdzie N jest liczbą otworów.

Wielościany Császár i Szilassi

Interaktywny model wielościanu Csaszar – na obrazie SVG poruszaj myszką w lewo iw prawo, aby go obracać.
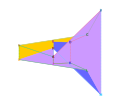
Interaktywny model wielościanu Szilassi – na obrazie SVG poruszaj myszą, aby go obrócić.

Dwie z najprostszych możliwych osadzonych wielościanów toroidalnych to wielościany Császár i Szilassi.

Császár wielościan jest siedem-vertex wielościan toroidalny z 21 krawędzi i 14 trójkątne twarze. To i czworościan są jedynymi znanymi wielościanami, w których każdy możliwy odcinek linii łączący dwa wierzchołki tworzy krawędź wielościanu. Jego podwójny, wielościan Szilassi , ma siedem heksagonalnych ścian, które sąsiadują ze sobą, co zapewnia istnienie połowy twierdzenia, że maksymalna liczba kolorów potrzebnych do mapy na torusie (rodzaju pierwszego) wynosi siedem.

Wielościan Császára ma najmniejszą możliwą liczbę wierzchołków ze wszystkich osadzonych wielościanów toroidalnych, a wielościan Szilassiego ma najmniejszą możliwą liczbę ścianek ze wszystkich osadzonych wielościanów toroidalnych.

Toroidy Stewarta

Specjalna kategoria wielościanów toroidalnych jest zbudowana wyłącznie z regularnych ścian wielokątów , bez przecięć, z dalszym ograniczeniem, że sąsiednie ściany nie mogą leżeć w tej samej płaszczyźnie. Są to tak zwane toroidy Stewarta , nazwane na cześć Bonnie Stewart , która intensywnie je badała. Są one analogiczne do brył Johnsona w przypadku wielościanów wypukłych ; jednak, w przeciwieństwie do brył Johnsona, istnieje nieskończenie wiele toroidów Stewarta. Należą do nich również deltaedry toroidalne , wielościany, których twarze są trójkątami równobocznymi.

Ograniczona klasa toroidów Stewarta, również zdefiniowana przez Stewarta, to quasi-wypukłe wielościany toroidalne . Są to toroidy Stewarta, które zawierają wszystkie krawędzie ich wypukłych kadłubów . W przypadku takiego wielościanu każda powierzchnia wypukłego kadłuba albo leży na powierzchni toroidu, albo jest wielokątem, którego wszystkie krawędzie leżą na powierzchni toroidu.

Toroidy Stewarta przez augmentację pojedynczego wielościanu
Rodzaj 1 1
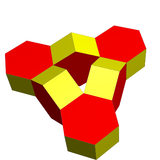
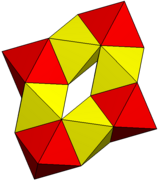
Obraz Stewart toroidalny 6-hexprisms.png Osiem ośmiościan toroid.png
Wielościany 6 sześciokątnych pryzmatów 8 oktaedrów
Wierzchołki 48 24
Krawędzie 84 72
Twarze 36 48
Quasi-wypukłe toroidy Stewarta
Rodzaj 1 3 11 3 5 7 11
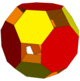
Obraz Wydobyty obcięty sześcian.png Wykopany ścięty ośmiościan1.png Wykopany ścięty ośmiościan2.png Wydobyty rozszerzony sześcian sześcienny.png Wydobyty skrócony sześcian sześcienny4.png Wydobyty skrócony sześcian sześcienny2.png Wydobyty skrócony sześcian sześcienny3.png Wydobyty skrócony sześcian sześcienny.png
Wielościany 4 kwadratowe kopuły
8 czworościanów 		6 trójkątnych kopuł
6 kwadratowych piramid 		4 trójkątne kopuły
6 kwadratowych piramid 		24 trójkątne graniastosłupy
6 ostrosłupów kwadratowych
8 czworościanów 		6 kwadratowych kopuł
4 trójkątne kopuły
12 kostek 		8 trójkątnych kopuł
12 kostek 		6 kwadratowych kopuł
12 kostek 		6 kwadratowych kopuł
8 trójkątnych kopuł
Wypukły kadłub ścięta kostka ścięty ośmiościan ścięty ośmiościan rozszerzony sześcian sześcienny ścięty sześcian sześcienny ścięty sześcian sześcienny ścięty sześcian sześcienny ścięty sześcian sześcienny
Wierzchołki 32 30 30 62 72 72 72 72
Krawędzie 64 60 72 168 144 168 168 168
Twarze 32 30 38 86 68 88 84 76

Wielościany samoprzekraczające

Oktahemioctahedron.png
Oktahemioktaedr 		Mały sześcienny ośmiościan.png
Mały prostopadłościan sześcienny 		Wielki dwunastościan.png
Świetny dwunastościan

Wielościan utworzony przez układ przecinających się wielokątów odpowiada abstrakcyjnej rozmaitości topologicznej utworzonej przez jej wielokąty i ich układ wspólnych krawędzi i wierzchołków, a rodzaj wielościanu można określić na podstawie tej abstrakcyjnej rozmaitości. Przykłady obejmują ośmiościan sześcienny z rodzaju 1, mały ośmiościan sześcienny z rodzaju 3 i dwunastościan wielki z rodzaju 4 .

Wielościany korony

Stephanoid pięciokątny. Ten stefanoid ma pięciokątną symetrię dwuścienną i ma takie same wierzchołki jak jednorodny graniastosłup pięciokątny .

Wielościan korony lub stephanoid jest toroidalny wielościan, który jest szlachetny , będąc isogonal (równe wierzchołki) i isohedral (równe twarzy). Wielościany korony są samoprzecinające się i topologicznie samopodwójne .

Zobacz też

Bibliografia

Linki zewnętrzne