Figura izoedryczna - Isohedral figure
W geometrii , A Polytope o wymiarach 3 (a polihedronu ) lub wyższa isohedral lub twarzą przechodnia , gdy wszystkie jej powierzchnie są takie same. Dokładniej, wszystkie ściany muszą być nie tylko przystające, ale muszą być przechodnie , tj. Muszą leżeć w tej samej orbicie symetrii . Innymi słowy, każdy stoi i B , musi istnieć symetria całe ciało stałe obroty i odbicia, które odwzorowuje A na B . Z tego powodu wypukłe wielościany izoedryczne to kształty, które pozwolą na wykonanie uczciwych kości .
Wielościany izoedryczne nazywane są izoedrami . Można je opisać konfiguracją twarzy . Formularz, który jest isohedral i ma regularne wierzchołków jest również krawędzi przechodnia (isotoxal) i mówi się, że quasiregular podwójny : Niektórzy teoretycy uważają te dane jako prawdziwie quasiregular ponieważ mają one te same symetrie, ale nie jest to powszechnie akceptowane. Izoedr ma parzystą liczbę ścian.
Wielościan, który jest izoedryczny, ma podwójny wielościan, który jest przechodni przez wierzchołki (izogonalny). Do substancji stałych Kataloński , że bipyramids i trapezohedra są isohedral. Są podwójnymi izogonalnymi archimedesowymi ciałami stałymi , odpowiednio pryzmatami i antypryzmatami . W Platońskie substancje stałe , które są albo samo podwójne lub podwójne z inną platońsko stałej, są wierzchołek, krawędź, a twarzą przechodni (isogonal, isotoxal i isohedral). Mówi się, że wielościan, który jest izoedryczny i izogonalny, jest szlachetny .
Nie wszystkie izozonoedry są izoedryczne. Przykład: rombowy dwudziestościan jest izozonoedrem, ale nie jest izoedrem.
Przykłady
| Wypukły | Wklęsły | ||
|---|---|---|---|
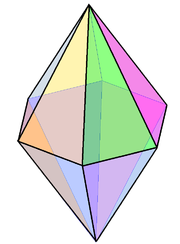 Sześciokątny podwójnej piramidy , V4.4.6 jest nieregularnego przykładem isohedral wielościanu. |
 Płytki pięciokątne izoedryczne Kairu , V3.3.4.3.4 |
 Rombowy dodecahedral plastra miodu jest przykładem isohedral (i izochoryczna), wypełniającymi przestrzeń plastra miodu. |
 Topologiczne kwadratowe kafelki zniekształcone w spiralne kształty H. |
Klasy izoedrów według symetrii
| Twarze | Konfiguracja twarzy . |
Klasa | Nazwa | Symetria | Zamówienie | Wypukły | Współpłaszczyznowy | Nie wypukłe |
|---|---|---|---|---|---|---|---|---|
| 4 | V3 3 | platoniczny |
czworościan tetragonalny disphenoid rombowy disphenoid |
T d , [3,3], (* 332) D 2d , [2 + , 2], (2 *) D 2 , [2,2] + , (222) |
24 4 4 4 |
 
|
||
| 6 | V3 4 | platoniczny |
sześcian trygonalny trapezoedr asymetryczny trapezoedr trygonalny |
O h , [4,3], (* 432) D 3d , [2 + , 6] (2 * 3) D 3 [2,3] + , (223) |
48 12 12 6 |
 
|
||
| 8 | V4 3 | platoniczny |
ośmiościan kwadratowy podwójnej piramidy rombowy podwójnej piramidy kwadratowy scalenohedron |
O h , [4,3], (* 432) D 4h , [2,4], (* 224) D 2h , [2,2], (* 222) D 2d , [2 + , 4], ( 2 * 2) |
48 16 8 8 |
    
|

|
|
| 12 | V3 5 | platoniczny |
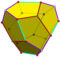
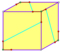
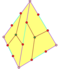
regularny dwunastościan pirydościan tetartoid |
I h , [5,3], (* 532) T h , [3 + , 4], (3 * 2) T, [3,3] + , (* 332) |
120 24 12 |
|
|
 
|
| 20 | V5 3 | platoniczny | dwudziestościan regularny | I h , [5,3], (* 532) | 120 |  |
||
| 12 | V3.6 2 | Kataloński | triakis czworościan | T d , [3,3], (* 332) | 24 |  |
 
|

|
| 12 | V (3,4) 2 | Kataloński |
dwunastościan rombowy dwunastościan deltoidalny |
O h , [4,3], (* 432) T d , [3,3], (* 332) |
48 24 |
  
|
 |
 
|
| 24 | V3.8 2 | Kataloński | triakis ośmiościan | O h , [4,3], (* 432) | 48 |  |
 
|
|
| 24 | V4.6 2 | Kataloński | sześcian tetrakis | O h , [4,3], (* 432) | 48 |
 
|
 
|
 
|
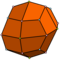
| 24 | V3.4 3 | Kataloński | deltoidal icositetrahedron | O h , [4,3], (* 432) | 48 |
|
  
|

|
| 48 | V4.6.8 | Kataloński | disdyakis dwunastościan | O h , [4,3], (* 432) | 48 |  |
  
|
 
|
| 24 | V3 4 .4 | Kataloński | pięciokątny dwudziestościan | O, [4,3] + , (432) | 24 |  |
||
| 30 | V (3,5) 2 | Kataloński | rombowy trójkontan | I h , [5,3], (* 532) | 120 |  |
||
| 60 | V3.10 2 | Kataloński | triakis dwudziestościan | I h , [5,3], (* 532) | 120 |  |
   
|
|
| 60 | V5.6 2 | Kataloński | dwunastościan pentakis | I h , [5,3], (* 532) | 120 |  |
    
|
|
| 60 | V3.4.5.4 | Kataloński | sześciokąt naramienny | I h , [5,3], (* 532) | 120 |  |
 |

|
| 120 | V4.6.10 | Kataloński | disdyakis triacontahedron | I h , [5,3], (* 532) | 120 |  |
  
|
  
|
| 60 | V3 4 .5 | Kataloński | pięciokątny sześciokąt | I, [5,3] + , (532) | 60 |  |
||
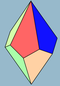
| 2 n | V3 3 . n | Polarny |
trapezoedr asymetryczny trapezoedr |
D nd , [2 + , 2 n ], (2 * n ) D n , [2, n ] + , (22 n ) |
4 n 2 n |
|
||
| 2 n 4 n |
V4 2 . n V4 2 .2 n V4 2 .2 n |
Polarny | regular n - bipiramid izotoksal 2 n -bipiramid 2 n - skalenoedr |
D n h , [2, n ], (* 22 n ) D n h , [2, n ], (* 22 n ) D n d , [2 + , 2 n ], (2 * n ) |
4 n |
  
|
   
|
k -izoedryczny postać
Wielościan (lub ogólnie polytop ) jest k- izoedryczny, jeśli zawiera k ścian w ramach swojej podstawowej domeny symetrii.
Podobnie płytka k- izoedryczna ma k oddzielnych orbit symetrii (i może zawierać m powierzchni o różnych kształtach dla niektórych m < k ).
Monohedral wielościan lub płytki monohedral ( m = 1), ma przystające powierzchnie, a zarówno bezpośrednie lub reflectively, które występują w jednym lub w większej ilości pozycji symetrii. R -hedral wielościany lub płytki ma r rodzajów ścian (nazywanych również trójkątne do dwuścian, 2 lub 3).
Oto kilka przykładów k-izoedrycznych wielościanów i nachyleń, z ich ścianami pokolorowanymi według ich pozycji k symetrii:
| 3-izoedryczny | 4-izoedryczny | izoedryczny | 2-izoedryczny |
|---|---|---|---|
| (2-hedral) wielościany o regularnej twarzy | Wielościany jednościenne | ||
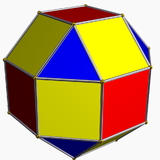
|
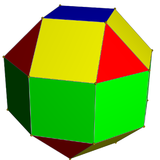
|
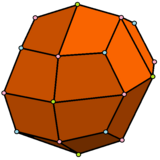
|
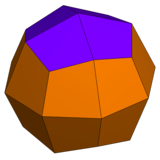
|
| Sześcio-ośmiościan rombowy mały ma 1 typu trójkąta i 2 typy pól | Pseudo-sześcio-ośmiościan rombowy mały ma 1 typu trójkąta 3 rodzaje pól. | Dwudziestoczterościan deltoidowy ma z 1 rodzaju twarzy. | Pseudo dwudziestoczterościan deltoidowy obejmuje 2 typy identycznych kształt twarzy. |
| 2-izoedryczny | 4-izoedryczny | Izoedryczny | 3-izoedryczny |
|---|---|---|---|
| (2-hedral) regularne dachówki | Spadki jednościenne | ||

|

|

|
|
| Pitagorasa Dachówka posiada 2 rozmiary kwadratów. | Ta 3-jednolita płytka ma 3 typy identycznych trójkątów i 1 rodzaj kwadratu. | Jodełkę ma 1 typu prostokątnej powierzchni. | Ta pięciokątna płytka ma 3 rodzaje identycznych nieregularnych ścian pięciokąta. |
Terminy pokrewne
Komórek przechodnia lub izochoryczna postać jest N - Polytope ( n > 3) lub o strukturze plastra miodu , która posiada komórki przystające i przechodnia ze sobą. W trójwymiarowych plastrach miodu, katoptryczne plastry miodu , podwójne do jednorodnych plastrów miodu, są izochoryczne. W 4 wymiarach izochoryczne polytopy zostały policzone do 20 komórek.
Aspekt-przechodnia lub izotopowe wielkość jest n -wymiarowych polytopes lub o strukturze plastra miodu, z aspektów (( n -1) - oblicza ) przystające i przechodnia. Podwójny o izotopu jest isogonal Polytope. Z definicji ta właściwość izotopowa jest wspólna dla podwójnych jednorodnych polytopów .
- Izotopowa dwuwymiarowa figura jest izotoksyczna (przechodnia przez krawędź).
- Izotopowa trójwymiarowa figura jest izoedryczna (przechodnia przez twarz).
- Izotopowa 4-wymiarowa figura jest izochoryczna (przechodnia przez komórkę).
Zobacz też
Uwagi
Bibliografia
- Peter R. Cromwell, Polyhedra , Cambridge University Press 1997, ISBN 0-521-55432-2 , s. 367 Przechodniość
Zewnętrzne linki
- Olshevsky, George. „Izotop” . Słowniczek hiperprzestrzeni . Zarchiwizowane od oryginału w dniu 4 lutego 2007 r.
- Weisstein, Eric W. "Płytki izoedryczne" . MathWorld .
- Weisstein, Eric W. „Isohedron” . MathWorld .
- izoedry 25 klas izoedrów o skończonej liczbie boków
- Dice Design w The Dice Lab


