Gosset-Elte Figurki - Gosset–Elte figures

4 ₂₁ Polytope 8 przestrzeń

W geometrii , że dane Gosset-Elte , nazwanych przez Coxeter'a po Thorold Gosset i EL Elte , to grupa jednolitych polytopes które nie są regularne , generowany przez konstrukcji Wythoff z lustrami wszystkich powiązanych kolejności-2 i rzędu-3 kąty dwuścienne. Mogą one być postrzegane jako jeden koniec obwódkami diagramów Coxeter-Dynkin .

Coxeter symbolu dla tych danych ma postać k _{i, j} , gdzie każda litera oznacza długość rzędu-3 oddziały na schemacie Coxeter-Dynkin z pojedynczym pierścieniem z węzła końcowego do k sekwencji długości rozgałęzień. Postać wierzchołka z k _{i, j} oznacza ( K  - 1) _{, j} , a każda z jego aspektów, są reprezentowane przez odjęcie jednej z jednego z niezerowych indeksów, tj k _{I  - 1, j} i k, _{I , J  - 1} .

Rektyfikowanego simplices są ujęte w wykazie jako ograniczenie przypadków z k = 0. Podobnie 0 _{I, J, K} reprezentuje rozgałęziony wykres z węzłem centralnym otoczonej pierścieniami.

Historia

Coxeter nazwał te dane jak k _{I, J} (lub k _ij ) w stenografii i dał kredyt na ich odkrycie Gosset i ELTE:

• Thorold Gosset pierwszy opublikował listę stałych i pół-stałych postaci w przestrzeni n wymiary w 1900 roku, wyliczając polytopes z jednego lub kilku rodzajów regularnych Polytope twarze. Obejmowało to naprawione 5-komórka 0 ₂₁ w 4 miejsca, demipenteract 1 ₂₁ w 5 przestrzeni, 2 ₂₁ w 6 przestrzeni, 3 ₂₁ w 7 przestrzeń, 4 ₂₁ na 8 przestrzeni i 5 ₂₁ nieskończonym tesselacji w 8 -przestrzeń.
• EL Elte niezależnie wyliczone inną listę semiregular w jego 1912 książce The Semiregular Polytopes tych Hyperspaces . Nazwał je semiregular polytopes pierwszego rodzaju , ograniczając jego poszukiwanie do jednego lub dwóch rodzajów stałych lub semiregular k-twarze.

Wyliczenie ELTE obejmowała wszystkie k _ij polytopes wyjątkiem 1 ₄₂ , który ma 3 typy 6-twarze.

Zbiorem cyfr rozciągają się plastrach (2,2,2), (3,3,1), (5,4,1) i rodzin 6,7,8 wymiarowych euklidesowych odpowiednio. Lista GOSSET za obejmował 5 ₂₁ plastra miodu jako jedyny semiregular jeden w jego definicji.

Definicja

Prosto splecione grupy ADE

W polytopes i plastrach z tej rodziny można rozpatrywać w klasyfikacji ADE .

Skończony Polytope k _ij jeśli istnieje

${\ Displaystyle {\ Frac {1} {I + 1}} + {\ Frac {1} {J + 1}} + {\ Frac {1} {k + 1}}> 1}$

lub równe dla euklidesowych plastrach, a mniej dla hiperbolicznych plastrach.

Grupa Coxeter [3 ^{, j, k} ] może generować do 3 wyjątkowe jednolitej Gosset-Elte dane ze schematów Coxeter-Dynkin z jednego węzła końcowego otoczonej pierścieniami. Przez Coxeter zapisu jest każda figura reprezentuje k _ij oznacza końcowego węzła w k -długość sekwencja jest pierścieniowy.

Simplex rodziny mogą być traktowane jako ograniczające przypadku z k = 0, a wszystkie wyprostowanego (jednopierścieniowe) schematów Coxeter-Dynkin.

A Family [3 ⁿ ] (wyprostowane simplices )

Rodzina n - simplices zawierać Gosset-Elte dane z formularza 0 _ij jak wszystkie rektyfikacji form n -simplex ( i  +  j  =  n  - 1).

Są one wymienione poniżej razem z ich schemacie Coxeter-Dynkin z każdej rodziny wymiarowej narysowany jako graficzny prostopadłym rzucie na płaszczyznę wielokąta Petrie regularnego simplex.

grupa Coxetera	Simplex	rektyfikowany	Birectified	Trirectified	Quadrirectified
1 [3 : 0 ]	= 0 00
2 [3 1 ]	= 0 10
3 [3 2 ]	= 0 20	= 0 11
4 [3 3 ]	= 0 30	= 0 21
5 [3 4 ]	= 0 40	= 0 31	= 0 22
6 [3 5 ]	= 0 50	= 0 41	= 0 32
7 [3 6 ]	= 0 60	= 0 51	= 0 42	= 0 33
8 [3 7 ]	= 0 70	= 0 61	= 0 52	= 0 43
9 [3 8 ]	= 0 80	= 0 71	= 0 62	= 0 53	= 0 44
10 [3 9 ]	= 0 90	= 0 81	= 0 72	= 0 63	= 0 54
...	...

D rodziny [3 ^{n -3,1,1} ] demihypercube

Każde d _n grupa ma dwie postaci Gosset-Elte, tym n - demihypercube jako 1 _K1 i naprzemiennej postaci N - orthoplex , k ₁₁ , wykonane z naprzemiennych simplex aspektów. Wyprostowany n - demihypercubes o niższy symetrii birectified n -CUBE może być również przedstawiony jako 0 _K11 .

Klasa	Demihypercubes	Orthoplexes (Zwykły)	rektyfikowanego demicubes
D 3 [3 1,1,0 ]	= 1 10		= 0 110
D 4 [3 1,1,1 ]	= 1 11		= 0 111
D 5 [3 2,1,1 ]	= 1 21	= 2 11	= 0 211
D 6 [3 3,1,1 ]	= 1 31	= 3 11	= 0 311
D 7 [3 4,1,1 ]	= 1 41	= 4 11	= 0 411
D 8 [3 5,1,1 ]	= 1 51	= 5 11	= 0 511
D 9 [3 6,1,1 ]	= 1 61	= 6 11	= 0 611
D 10 [3 7,1,1 ]	= 1 71	= 7 11	= 0 711
...	...	...
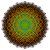
D N [3 n -3,1,1 ]	... = 1 n -3,1	... = ( n -3) 11	... = 0 n -3,1,1

E _n rodziny [3 ^{n -4,2,1} ]

Każdy E _n grupy od 4 do 8 ma dwa lub trzy postacie Gosset-Elte reprezentowanego przez jeden z węzłów końcowych pierścieniowych: k _{: 21} , 1 _k2 , 2 _K1 . Wyprostowanego 1 _K2 seria może być również przedstawiony jako 0 _K21 .

	2 k1	1 k2	k 21	0 K21
E 4 [3 0,2,1 ]	= 2 01	= 1 20	= 0 21
E 5 [3 1,2,1 ]	= 2 11	= 1 21	= 1 21	= 0 211
E 6 [3 2,2,1 ]	= 2 21	= 1 22	= 2 21	= 0 221
E 7 [3 3,2,1 ]	= 2 31	= 1 32	= 3 21	= 0 321
PL 8 [3 4,2,1 ]	= 2 41	= 1 42	= 4 21	= 0 421

Euklidesowe i hiperboliczne plastrach

Istnieją trzy euklidesowa ( afiniczne ) grupy Coxeter wymiarach 6, 7 i 8:

grupa Coxetera	plastrach
${\ Displaystyle {\ tylda {E}} _ {6}}$= [3 2,2,2 ]	= 2 22			= 0 222
${\ Displaystyle {\ tylda {E}} _ {7}}$= [3 3,3,1 ]	= 3 31	= 1 33		= 0 331
${\ Displaystyle {\ tylda {E}} _ {8}}$= [3 5,2,1 ]	= 2 51	= 1 52	= 5 21	= 0 521

Istnieją trzy hiperboliczne ( parazwartą ) grupy Coxeter wymiarach 7, 8 i 9:

grupa Coxetera	plastrach
${\ Displaystyle {\ bar {T}} _ {7}}$= [3 3,2,2 ]	= 3 22	= 2 32		= 0 322
${\ Displaystyle {\ bar {T}} _ {8}}$= [3 4,3,1 ]	= 4 31	= 3 41	= 1 43	= 0 431
${\ Displaystyle {\ bar {T}} _ {9}}$= [3 6,2,1 ]	= 2 61	= 1 62	= 6 21	= 0 621

Jako dalsze uogólnienie zamówień 3 rozgałęzień mogą być także wyrażone w tym symbolu. 4-wymiarowej afinicznej grupa Coxeter , [3 ^1,1,1,1 ] cztery zleceniem 3 gałęzie, i mogą wyrażać jedną strukturze plastra miodu, 1 ₁₁₁ , , oznacza niższą formę symetrii plastra miodu 16 komórek i 0 ₁₁₁₁ , do wyprostowanego plastra miodu 16 komórek . 5-wymiarowej hiperboliczny grupa Coxeter , [3 ^1,1,1,1,1 ], posiada pięć zleceniem 3 gałęzie, i mogą wyrażać jedną strukturze plastra miodu, 1 ₁₁₁₁ , i jego korektę w postaci 0 ₁₁₁₁₁ , . ${\ Displaystyle {\ tylda {P}} _ {4}}$${\ Displaystyle {\ bar {l}} _ {4}}$

Uwagi

Referencje

• Gosset, Thorold (1900). „Na pół-stałych i regularnych figur w przestrzeni n wymiarów”. Komunikator Matematyki . 29 : 43 & ndash 48.
• Elte, EL (1912), The Semiregular Polytopes tych Hyperspaces , Groningen: University of Groningen, ISBN  1-4181-7968-X[1], [2]
• Coxeter, HSM (3rd edition, 1973) Regularne Polytopes , wydanie Dover, ISBN  0-486-61480-8
• Norman Johnson Uniform Polytopes , rękopis (1991)
  • NW Johnson : The Theory of Uniform Polytopes i Honeycombs , Ph.D. Rozprawa, University of Toronto, 1966