Rektyfikowanego 5-kostki - Rectified 5-cubes

5-cube	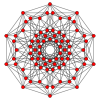Rektyfikowany 5-cube	Birectified 5-cube Birectified 5-orthoplex
5-orthoplex	Rektyfikowany 5-orthoplex
Rzutami w A 5 Coxeter płaszczyźnie

W pięć-wymiarowej geometrii , o naprawione 5-kostka jest wypukła jednolite 5-Polytope , będąc sprostowanie regularnej 5-cube .

Istnieje 5 stopni sprostowania w 5-Polytope The zerowego tutaj będąc 5-sześcian , a 4 i ostatni będąc 5-orthoplex . Wierzchołki wyprostowanego 5-kostki znajdują się na brzegowych ośrodków 5-cube. Wierzchołki birectified 5-ocube znajdują się w kwadratowych centrów oblicze 5-cube.

Rektyfikowany 5-cube

Rektyfikowany 5-cube naprawione penteract (Rin)
Rodzaj	jednolite 5 Polytope
symbol schläfliego	R {4,3,3,3}
Coxeter schemat	=
4-twarze	42
Komórki	200
twarze	400
Obrzeża	320
wierzchołki	80
Vertex figura	czworościenny pryzmat
grupa Coxetera	B 5 [4,3 3 ] Kolejność 3840
Podwójny
Punkt bazowy	(0,1,1,1,1,1) √2
circumradius	sqrt (2) = 1,414214
Nieruchomości	wypukły , isogonal

nazwy alternatywne

• Rektyfikowany penteract (akronim: Rin) (Jonathan Bowers)

Budowa

Wyprostowane 5 kostka może być wykonana z 5-kostki przez obcinanie wierzchołki w punktach środkowych krawędzi.

współrzędne

Te współrzędne kartezjańskie wierzchołków wyprostowanego 5-sześcianu o długości krawędzi jest przez wszystkie kombinacje: ${\ Displaystyle {\ sqrt {2}}}$

${\ Displaystyle (0 \ \ Pm 1 \ \ Pm 1 \ \ Pm 1 \ \ Pm 1)}$

Obrazy

ortograficznych prognozy

Coxeter samolot	B 5	B 4 / C 5	B 3 / C 4 / A 2
Wykres
dwuścienny symetria	[10]	[8]	[6]
Coxeter samolot	B 2	3
Wykres
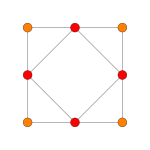
dwuścienny symetria	[4]	[4]

Birectified 5-cube

Birectified 5-cube birectified penteract (NIT)
Rodzaj	jednolite 5 Polytope
symbol schläfliego	2r {4,3,3,3}
Coxeter schemat	=
4-twarze	42	10 {3,4,3} 32 T1 {3,3,3}
Komórki	280
twarze	640
Obrzeża	480
wierzchołki	80
Vertex figura	{3} x {4}
grupa Coxetera	B 5 [4,3 3 ] Kolejność 3840 D 5 [3 2,1,1 ] Kolejność 1920
Podwójny
Punkt bazowy	(0,0,1,1,1,1) √2
circumradius	sqrt (3/2) = 1,224745
Nieruchomości	wypukły , isogonal

EL Elte zidentyfikować go w 1912 jako semiregular Polytope, określając go jako Cr ₅ ² w drugiej rektyfikacji 5-wymiarowym przekroju Polytope .

nazwy alternatywne

• Birectified 5-cube / penteract
• Birectified pentacross / 5-orthoplex / triacontiditeron
• Penteractitriacontiditeron (akronim: nit) (Jonathan Bowers)
• Rektyfikowany 5-demicube / demipenteract

Budowa i współrzędne

Birectified 5 kostka może być wykonana przez birectifing wierzchołki 5-sześcianu na długości krawędzi. ${\ Displaystyle {\ sqrt {2}}}$

Te współrzędne kartezjańskie w wierzchołkach birectified pięciu kostek o długości krawędzi 2 są wszystkie kombinacje:

${\ Displaystyle \ lewo (0 \ 0 \ \ Pm 1 \ \ Pm 1 \ \ Pm 1 \ prawej)}$

Obrazy

ortograficznych prognozy

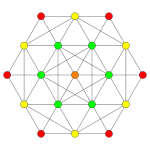
Coxeter samolot	B 5	B 4 / C 5	B 3 / C 4 / A 2
Wykres
dwuścienny symetria	[10]	[8]	[6]
Coxeter samolot	B 2	3
Wykres
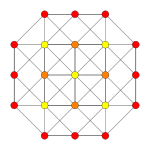
dwuścienny symetria	[4]	[4]

Powiązane polytopes

2 izotopowe hipersześcianach

Ciemny.	2	3	4	5	6	7	8	n
Imię	T {4}	R {4,3}	2t {4,3,3}	2r {4,3,3,3}	3t {4,3,3,3,3}	3r {4,3,3,3,3,3}	4t {4,3,3,3,3,3,3}	...
Coxeter schemat
Obrazy
fasety		{3}, {4}	T {3,3} t {3,4}	R {3,3,3} R {3,3,4}	2t {3,3,3,3} 2t {3,3,3,4}	2r {3,3,3,3,3} 2R {3,3,3,3,4}	3t {3,3,3,3,3,3} 3t {3,3,3,3,3,4}
Vertex figura	() V ()	{} {X}	{} {V}	{3} x {4}	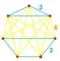{3} v {4}	{3,3} x {3,4}	{3,3} v {3,4}

Powiązane polytopes

Te polytopes są częścią 31 jednolitego polytera wytwarzanej z regularnej 5-cube lub 5-orthoplex .

B5 polytopes
β 5	t 1 β 5	T 2 γ 5	t 1 γ 5	γ 5	T 0,1 β 5	T 0,2 β 5	T 1,2 β 5
T 0,3 β 5	T 1,3 γ 5	T 1,2 γ 5	T 0,4 γ 5	T 0,3 γ 5	T 0,2 γ 5	T 0,1 γ 5	t 0,1,2 β 5
t 0,1,3 β 5	t 0,2,3 β 5	t 1,2,3 γ 5	t 0,1,4 β 5	t 0,2,4 γ 5	t 0,2,3 γ 5	t 0,1,4 γ 5	t 0,1,3 γ 5
t 0,1,2 γ 5	t 0,1,2,3 β 5	t 0,1,2,4 β 5	t 0,1,3,4 γ 5	t 0,1,2,4 γ 5	t 0,1,2,3 γ 5	t 0,1,2,3,4 γ 5

Uwagi

Referencje

• HSM Coxeter :
  • HSM Coxeter, regularne Polytopes , 3rd Edition, Dover New York, 1973
  • Kalejdoskop: Pisma wybrane HSM Coxeter'a pod redakcją F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Azji IVIC Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, regularne i naczep Zwykły Polytopes I [Math. Zeit. 46 (1940) 380-407 MR 2,10]
    • (Papier 23) HSM Coxeter, regularne i semi-Regular Polytopes II [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, regularne i semi-Regular Polytopes III [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , rękopis (1991)
  • NW Johnson: The Theory of Uniform Polytopes i Honeycombs , Ph.D.
• Klitzing Richard. "5d jednolite polytopes (polytera)" . o3x3o3o4o - Rin, o3o3x3o4o - nit

Linki zewnętrzne

• Polytopes o różnych wymiarach
• Słowniczek wielowymiarowe