Skrócony tesserakt - Truncated tesseract

Teserakt	Skrócony tesserakt	Teserakt rektyfikowany	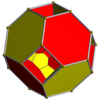Bitruncated tesseract
Diagramy Schlegla wyśrodkowane na [4,3] (komórki widoczne w [3,3])
16-ogniwowy	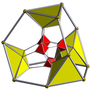Skrócona 16-ogniwowa	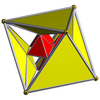Rektyfikacja 16-ogniwowa ( 24-ogniwowa )	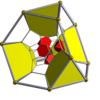Bitruncated tesseract
Diagramy Schlegla wyśrodkowane na [3,3] (komórki widoczne w [4,3])

W geometrii , A ściętego tesserakt jest jednorodna 4-Polytope wykonane jako skrócenie regularnego tesserakt .

Istnieją trzy obcięcia, w tym obcięcie bitów i obcięcie, które tworzy obcięty 16-komorowy .

Skrócony tesserakt

Skrócony tesserakt
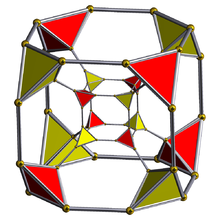Diagram Schlegla ( widoczne komórki czworościanu )
Rodzaj	Jednolity 4-politop
Symbol Schläfli	t{4,3,3}
Diagramy Coxetera
Komórki	24	8 3.8.8 16 3.3.3
Twarze	88	64 {3} 24 {8}
Krawędzie	128
Wierzchołki	64
Figura wierzchołka	( )v{3}
Podwójny	Tetrakis 16-ogniwowy
Grupa symetrii	B 4 , [4,3,3], rząd 384
Nieruchomości	wypukły
Jednolity indeks	12 13 14

Obcięty tesserakt jest ograniczony o 24 komórek : 8 obciętych kostki i 16 czworościanów .

Nazwy alternatywne

• Skrócony tesserakt ( Norman W. Johnson )
• Skrócony tesserakt (Skrót tat) (George Olshevsky i Jonathan Bowers)

Budowa

Obcięty tesserakt może być skonstruowany przez obcięcie wierzchołków teseraktu na długości krawędzi. Na każdym ściętym wierzchołku tworzy się regularny czworościan. ${\ Displaystyle 1/({\ sqrt {2}} + 2)}$

Te współrzędne kartezjańskie wierzchołków ściętego tesserakt o długości krawędzi 2 przedstawiono wszystkich permutacji:

${\ Displaystyle \ lewo (\ pm 1, \ \ pm (1+ {\ sqrt {2}}), \ \ pm (1+ {\ sqrt {2}}), \ \ pm (1+ {\ sqrt {} 2}})\prawo)}$

Projekcje

Stereoskopowej projekcji 3D ściętego tesserakt.

W pierwszym równoległym rzucie ściętego sześcianu ściętego teseraktu w przestrzeń trójwymiarową obraz jest ułożony w następujący sposób:

• Koperta projekcyjna to sześcian .
• Dwie z obciętych komórek sześcianu wystają na obcięty sześcian wpisany w sześcienną kopertę.
• Pozostałe 6 ściętych sześcianów wystaje na kwadratowe powierzchnie koperty.
• Osiem czworościennych objętości między kopertą a trójkątnymi ścianami centralnego ściętego sześcianu to obrazy 16 czworościanów, para komórek na każdy obraz.

Obrazy

rzuty ortogonalne

Samolot Coxetera	B 4	B 3 / D 4 / A 2	B 2 / D 3
Wykres
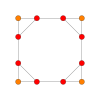
Symetria dwuścienna	[8]	[6]	[4]
Samolot Coxetera	F 4	3
Wykres
Symetria dwuścienna	[12/3]	[4]

Wielościanów netto

Skrócony tesserakt rzutowany na 3-sferę ze stereograficzną projekcją na 3-przestrzeń.

Powiązane politopy

Obcięty tesserakt jest trzecią sekwencją obciętych hipersześcianach :

Ścięte hipersześciany

Obraz								...
Nazwa	Ośmiokąt	Obcięta kostka	Skrócony tesserakt	Skrócona 5-kostka	Obcięty 6-kostkowy	Skrócona 7-kostka	Skrócona 8-kostka
Schemat Coxetera
Figura wierzchołka	( )v( )	( )v{ }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3,3}	( )v{3,3,3,3,3}

Bitruncated tesseract

Bitruncated tesseract
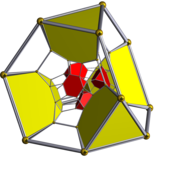Dwa diagramy Schlegla , wyśrodkowane na skróconych komórkach czworościennych lub skróconych ośmiościennych, z ukrytymi alternatywnymi typami komórek.
Rodzaj	Jednolity 4-politop
Symbol Schläfli	2t{4,3,3} 2t{3,3 1,1 } godz. 2,3 {4,3,3}
Diagramy Coxetera	=
Komórki	24	8 4,6,6 16 3,6,6
Twarze	120	32 {3} 24 {4} 64 {6}
Krawędzie	192
Wierzchołki	96
Figura wierzchołka	Digonal disfenoid
Grupa symetrii	B 4 , [3,3,4], rząd 384 D 4 , [3 1,1,1 ], rząd 192
Nieruchomości	wypukły , wierzchołek-przechodni
Jednolity indeks	15 16 17

Internet

Bitruncated tesserakt , bitruncated 16-komórka lub tesseractihexadecachoron jest wykonana przez bitruncation działania zastosowanego do tesserakt . Można go również nazwać teseraktem runcikantycznym z połową wierzchołków teseraktu runcikantelowego z budowa.

Nazwy alternatywne

• Bitruncated tesseract/Runcicantic tesseract ( Norman W. Johnson )
• Tesseractihexadecachoron (Skrót tah) (George Olshevsky i Jonathan Bowers)

Budowa

Tesserakt jest przycinany bitowo poprzez obcinanie jego komórek poza ich punkty środkowe, zamieniając osiem sześcianów w osiem skróconych oktaedrów . Te nadal mają kwadratowe twarze, ale sześciokątne twarze tworzą ścięte czworościany, które dzielą ze sobą trójkątne twarze.

Te współrzędne kartezjańskie w wierzchołkach bitruncated tesserakt o długości krawędzi 2 przedstawiono wszystkich permutacji:

${\ Displaystyle \ lewo (0, \ \ pm {\ sqrt {2}} \ \ pm 2 {\ sqrt {2}} \ \ pm 2 {\ sqrt {2}} \ prawej)}$

Struktura

Ścięte ośmiościany są połączone ze sobą poprzez swoje kwadratowe powierzchnie, a ze ściętymi czworościanami poprzez ich sześciokątne powierzchnie. Ścięte czworościany są połączone ze sobą trójkątnymi ścianami.

Projekcje

rzuty ortogonalne

Samolot Coxetera	B 4	B 3 / D 4 / A 2	B 2 / D 3
Wykres
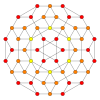
Symetria dwuścienna	[8]	[6]	[4]
Samolot Coxetera	F 4	3
Wykres
Symetria dwuścienna	[12/3]	[4]

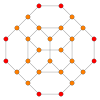
Projekcje stereograficzne

Pierwsza projekcja ściętego ośmiościanu teseraktu ściętego bitowo w przestrzeń 3D ma obciętą sześcienną obwiednię. Dwie ze ściętych komórek oktaedrycznych wystają na ścięty ośmiościan wpisany w tę otoczkę, przy czym kwadratowe ścianki dotykają środków ścian oktaedrycznych. 6 ścian oktaedrycznych to obrazy pozostałych 6 obciętych komórek oktaedrycznych. Pozostałą lukę między wpisanym ściętym ośmiościanem a otoczką wypełnia 8 spłaszczonych ściętych czworościanów, z których każdy jest obrazem pary ściętych czworościanów.

Projekcje stereograficzne

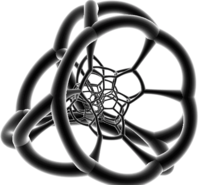
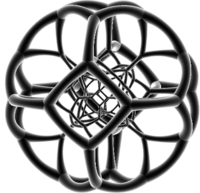
Kolorowe przezroczyste z różowymi trójkątami, niebieskimi kwadratami i szarymi sześciokątami

Powiązane politopy

Bitruncated tesserakt jest drugim w kolejności bitruncated hipersześcianach :

Hipersześciany bitruncowane

Obraz							...
Nazwa	Bitruncated kostka	Bitruncated tesseract	Bitruncated 5-kostek	Bitruncated 6-kostek	Bitruncated 7-kostek	Bitruncated 8-kostek
Coxeter
Figura wierzchołka	( )v{ }	{} w {}	{}w{3}	{}v{3,3}	{}v{3,3,3}	{}v{3,3,3,3}

Skrócona 16-ogniwowa

Skrócony 16-komórkowy tesserakt Cantic
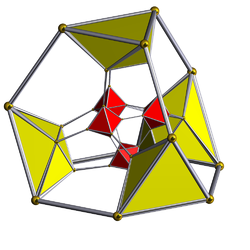Diagram Schlegla ( widoczne komórki ośmiościanu )
Rodzaj	Jednolity 4-politop
Symbol Schläfli	t{4,3,3} t{3,3 1,1 } godz. 2 {4,3,3}
Diagramy Coxetera	=
Komórki	24	8 3.3.3.3 16 3.6.6
Twarze	96	64 {3} 32 {6}
Krawędzie	120
Wierzchołki	48
Figura wierzchołka	kwadratowa Piramida
Podwójny	Teserakt Hexakis
Grupy Coxetera	B 4 [3,3,4], rząd 384 D 4 [3 1,1,1 ], rząd 192
Nieruchomości	wypukły
Jednolity indeks	16 17 18

Obcięty 16 komórek , obcięte hexadecachoron , cantic tesserakt , którego granice wyznaczają 24 komórek : 8 regularnych ośmiościennych i 16 ściętego czworościanów . Ma połowę wierzchołków kantelowego teseraktu z konstrukcją.

Jest spokrewniony, ale nie należy go mylić z 24-komorowym , który jest regularnym 4-politopem ograniczonym 24 regularnymi ośmiościanami.

Nazwy alternatywne

• Skrócony teserakt 16 komórek/kantyk ( Norman W. Johnson )
• Skrócony heksadecachoron (akronim thex) (George Olshevsky i Jonathan Bowers)

Budowa

Obcięta 16-komórka może być skonstruowana z 16-komórki przez obcięcie jej wierzchołków na 1/3 długości krawędzi. Daje to 16 skróconych komórek czworościennych i wprowadza 8 oktaedrów (figury wierzchołków).

(Obcięcie 16-komórki na 1/2 długości krawędzi daje 24-komórkę , która ma większy stopień symetrii, ponieważ obcięte komórki stają się identyczne z figurami wierzchołków.)

Te współrzędne kartezjańskie wierzchołków ściętego 16 komórek o długości krawędzi √2 podane są wszystkie permutacje i kombinacje Znak

(0,0,1,2)

Alternatywna konstrukcja zaczyna się od demisseraktu o współrzędnych wierzchołków (±3,±3,±3,±3), mającego parzystą liczbę każdego znaku, i obcina go, aby uzyskać permutacje

(1,1,3,3), z parzystą liczbą każdego znaku.

Struktura

Ścięte czworościany są połączone ze sobą przez ich sześciokątne powierzchnie. Oktaedry są połączone ze ściętymi czworościanami poprzez ich trójkątne powierzchnie.

Projekcje

Wyśrodkowany na oktaedrze

Oktaedron-pierwszy rzut równoległy w 3 wymiarach, z podświetlonymi komórkami oktaedrycznymi

Pierwsza równoległa projekcja ośmiościanu obciętej 16-komórki w trójwymiarową przestrzeń ma następującą strukturę:

• Obwiednia projekcji jest ściętym ośmiościanem .
• 6 kwadratowych ścian koperty to obrazy 6 komórek oktaedrycznych.
• Ośmiościan leży w środku obwiedni, połączony ze środkiem 6 kwadratowych ścian 6 krawędziami. To jest obraz pozostałych 2 komórek oktaedrycznych.
• Pozostałą przestrzeń między kopertą a centralnym ośmiościanem wypełnia 8 ściętych czworościanów (zniekształconych przez rzut). Są to obrazy 16 skróconych komórek czworościennych, pary komórek na każdy obraz.

Ten układ komórek w rzucie jest analogiczny do układu ścian w rzucie ściętego ośmiościanu w przestrzeń dwuwymiarową. W związku z tym ściętą 16 komórkę można uznać za 4-wymiarowy analog ściętego ośmiościanu.

Wyśrodkowany na ściętym czworościanie

Projekcja skróconej 16-komórki w 3 wymiarach, wyśrodkowana na skróconej komórce czworościennej, z usuniętymi komórkami ukrytymi

Ścięty czworościan pierwszy równoległy rzut ściętej 16-komórki w trójwymiarową przestrzeń ma następującą strukturę:

• Koperta rzutu jest ściętym sześcianem .
• Najbliższy ścięty czworościan do punktu obserwacji 4D rzutuje na środek obwiedni, z jego trójkątnymi ścianami połączonymi z 4 objętościami oktaedrycznymi, które łączą go z 4 trójkątnymi ścianami obwiedni.
• Pozostałą przestrzeń w kopercie wypełniają 4 inne ścięte czworościany.
• Te tomy są obrazami komórek leżących po bliższej stronie ściętej 16-komórki; pozostałe komórki rzutują na ten sam układ, z wyjątkiem konfiguracji podwójnej.
• Sześć ośmiokątnych ścian obwiedni projekcji to obrazy pozostałych 6 ściętych komórek czworościennych.

Obrazy

rzuty ortogonalne

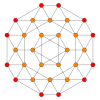
Samolot Coxetera	B 4	B 3 / D 4 / A 2	B 2 / D 3
Wykres
Symetria dwuścienna	[8]	[6]	[4]
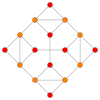
Samolot Coxetera	F 4	3
Wykres
Symetria dwuścienna	[12/3]	[4]

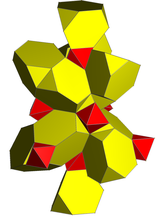Internet

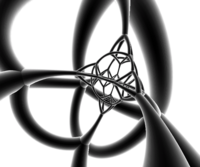Projekcja stereograficzna (wyśrodkowana na ściętym czworościanie )

Powiązane politopy

Obcięta 16-komórka, jako sześcian kantic 4-, jest związana z wymiarową rodziną n-sześcianów kantic:

Rodzina wymiarowa n-sześcianów kantycznych

n	3	4	5	6	7	8
Symetria [1 + ,4,3 n-2 ]	[1 + ,4,3] = [3,3]	[1 + ,4,3 2 ] = [3,3 1,1 ]	[1 + ,4,3 3 ] = [3,3 2,1 ]	[1 + ,4,3 4 ] = [3,3 3,1 ]	[1 + ,4,3 5 ] = [3,3 4,1 ]	[1 + ,4,3 6 ] = [3,3 5,1 ]
Postać kantycka
Coxeter	=	=	=	=	=	=
Schläfli	godz. 2 {4,3}	h 2 {4,3 2 }	h 2 {4,3 3 }	h 2 {4,3 4 }	h 2 {4,3 5 }	godz. 2 {4,3 6 }

Powiązane jednolite politopy

Powiązane jednolite politopy w symetrii demitesseract

D 4 jednolita polichora
{3,3 1,1 } godz.{4,3,3}	2r{3,3 1,1 } h 3 {4,3,3}	t{3,3 1,1 } godz. 2 {4,3,3}	2t{3,3 1,1 } godz. 2,3 {4,3,3}	r{3,3 1,1 } {3 1,1,1 } = {3,4,3}	rr{3,3 1,1 } r{3 1,1,1 }=r{3,4,3}	tr{3,3 1,1 } t{3 1,1,1 }=t{3,4,3}	sr{3,3 1,1 } s{3 1,1,1 }=s{3,4,3}

Powiązane jednolite politopy w symetrii tesseract

Politopy symetrii B4
Nazwa	tesseract	rektyfikowany tesseract	obcięty tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	wszechskrócony tesseractser
Schemat Coxetera		=				=
Symbol Schläfli	{4,3,3}	t 1 {4,3,3} r{4,3,3}	t 0,1 {4,3,3} t{4,3,3}	t 0,2 {4,3,3} rr{4,3,3}	t 0,3 {4,3,3}	t 1,2 {4,3,3} 2t{4,3,3}	t 0,1,2 {4,3,3} s {4,3,3}	t 0,1,3 {4,3,3}	t 0,1,2,3 {4,3,3}
Schemat Schlegla
B 4
Nazwa	16-ogniwowy	rektyfikowane 16-ogniwowe	skrócona 16-ogniwowa	kantelowy 16-ogniwowy	uruchomiony 16-komorowy	bitruncated 16-komorowy	cantitruncated 16-komorowy	skrócony 16-komorowy	wszechstronnie skrócony 16-ogniwowy
Schemat Coxetera	=	=	=	=		=	=
Symbol Schläfli	{3,3,4}	t 1 {3,3,4} r{3,3,4}	t 0,1 {3,3,4} t{3,3,4}	t 0,2 {3,3,4} rr{3,3,4}	t 0,3 {3,3,4}	t 1,2 {3,3,4} 2t{3,3,4}	t 0,1,2 {3,3,4} s {3,3,4}	t 0,1,3 {3,3,4}	t 0,1,2,3 {3,3,4}
Schemat Schlegla
B 4

Uwagi

Bibliografia

• T. Gosset : O regularnych i półregularnych figurach w przestrzeni n wymiarów , Messenger of Mathematics, Macmillan, 1900
• HSM Coxeter :
  • Coxeter, Regular Polytopes , (3 wydanie, 1973), wydanie Dover, ISBN  0-486-61480-8 , s. 296, Tabela I (iii): Regularne Polytopes, trzy regularne polytopes w n-wymiarach (n≥5)
  • HSM Coxeter, Regular Polytopes , wydanie trzecie, Dover New York, 1973, s. 296, Tabela I (iii): Regularne Polytopes, trzy regularne polytopes w n-wymiarach (n≥5)
  • Kalejdoskopy: Wybrane pisma HSM Coxeter , pod redakcją F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • ( Praca 22) HSM Coxeter, Regular i Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • ( Praca 23) HSM Coxeter, Regularne i półregularne Polytopes II , [ Mat . Zeit. 188 (1985) 559-591]
    • ( Praca 24) HSM Coxeter, Regularne i półregularne Polytopes III , [ Mat . Zeit. 200 (1988) 3-45]
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, Symetrie rzeczy 2008, ISBN  978-1-56881-220-5 (Rozdział 26. s. 409: Hemikuby: 1 _n1 )
• Norman Johnson Uniform Polytopes , Rękopis (1991)
  • NW Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
• 2. Wypukła jednolita polichora oparta na tesserakcie (8-komorowym) i hexadecachoron (16-komorowym) - Modele 13, 16, 17 , George Olshevsky.
• Klitzing, Richard. "Polytopy jednolite 4D (polichora)" . o3o3o4o - tata, o3x3x4o - tah, x3x3o4o - thex

Linki zewnętrzne

• Papierowy model obciętego teseraktu stworzony przy użyciu siatek generowanych przez oprogramowanie Stella4D